滚动轴承的退化状态划分与剩余寿命预测

隋文涛，张 丹，金亚军，邱晓梅

（1.山东理工大学机械工程学院，山东 淄博 255000；2.山东理工大学电气与电子工程学院，山东 淄博 255000）

1 引言

滚动轴承的剩余寿命预测[1]在设备管理与维修中起着重要作用，根据设备的退化状态准确地进行剩余寿命预测是制定轴承故障维修决策的关键。文献[2]利用SVM识别离心泵滚动轴承的故障，同时用遗传算法对SVM模型参数进行优化，将从原始信号和边际积分比例图中提取的故障特征作为SVM 模型的输入向量，选择用训练完成的分类模型进行故障的诊断。

文献[3]将SVM 与经验模态分解（EMD）相结合，通过计算EMD分解出的模态分量的能量，在识别城轨列车滚动轴承的故障类型上取得了准确有效的效果。文献[4]将SVM与小波包分析理论结合，提出一种以小波包分解[5]后子带信号能量与所有信号总能量之比为特征向量，进而对轴承故障进行诊断。

考虑到差分算法[6]易于使用、速度快、鲁棒性等优点，利用这些优点可以更加快速有效的对轴承振动信号进行划分，所以，提出了一种基于支持向量回归[7]和差分进化算法结合的方法来预测滚动轴承的剩余寿命。

2 支持向量机回归原理

SVM 是利用核函数把原始变量由低维空间映射到高维空间，从而使得线性不可分样本转化成线性可分样本，在高维空间构造线性函数实现线性回归，得到原始空间中的非线性回归估计[8]。支持向量回归是支持向量机最普遍的应用形式，回归估计问题可以在形式上转化为函数y=（fx）的推断问题。给定训练集，X={(xi，yi)，i= 1，2，…，n} ，训练集中的xi∈Rn为输入变量，yi∈Rn为预测值，n为样本的个数。支持向量回归函数被定义为：

式中：wTϕ(xi)—向量点乘；b∈R—偏置门限，在式wTϕ(xi)中：

3 回归模型核函数与参数优化选择

确定回归模型的参数是回归模型在滚动轴承剩余寿命预测时首先要解决的问题，它也决定着预测结果的准确率。回归模型的相关参数主要是惩罚因子C和高斯径向基函数的宽度参数σ，惩罚因子C决定模型的复杂度，核函数宽度参数σ控制映射函数的径向作用区域。因此在训练回归模型之前，需要选择合适的模型参数，以找到最优参数来进行回归预测算法。常用的交叉验证参数选择法，能够搜索全局最优参数，但搜索量大而且比较耗时。本文使用差分进化算法来搜寻SVM回归模型中两个重要参数组合（C，σ）的最优值。

考虑到DE算法的全局寻优能力，以均方误差最小化为优化准则建立目标函数，MSE的计算公式为：

式中：σ—SVM模型的第i个样本预测输出值；σ—第i个样本真实输出值。

基于DE算法的SVM回归模型参数寻优具体步骤为：

（1）初始化种群，设置当前代数g=0，确定种群数量、最大循环迭代次数、变异算子、交叉算子以及SVM惩罚参数C和核函数参数σ上下限值，随机产生参数组合（C，σ）。

（2）将（1）中的（C，σ）作为SVM预测模型的参数，进行样本训练和预测，得到预测结果。

（3）计算预测值和实际值计算目标函数，判断是否满足结束条件或者已经达到了最大进化代数：若满足以上条件，则终止进化，跳转到步骤（6）；否则，继续进行下一步操作。

（4）g=g+1，进入下一代进化，进行变异、交叉和选择操作，生成新的实验对象。

（5）重新计算实验对象的目标函数值，得到新的（C，σ），转至步骤（2）。

（6）输出最优参数组合（C，σ），最后进行SVM模型的样本训练和预测。

4 试验数据分析

在滚动轴承整个寿命周期中，从它开始投入机械设备使用到发生故障直至完全失效，要经历性能逐渐衰退的退化演变阶段。PRONOSTIA加速寿命试验平台轴承1−1加速度在全寿命周期内的波动变化过程，如图1所示。从图中的划分可以看出轴承退化过程主要包括三个状态：平稳磨合状态、衰退状态、失效故障状态。在状态I中，加速度在−2g和2g之间上下波动且趋于平稳，这段变化称为平稳磨合期；在状态II中，幅值在区间−10g到10g逐渐变化，这时的加速度幅值变化逐渐增大，这段退化趋势称为衰退期；在状态III中，加速度幅值在短时间内迅速增大，直到达到加速度阈值后引起轴承失效，这段退化趋势称为失效故障期。

图1 轴承振动信号波形图Fig.1 Bearing Vibration Signal Waveform

以上轴承三种状态的划分只是根据加速度信号的幅值变化特点进行大致划分，轴承状态I、状态II和状态III的分界线十分模糊。在进行轴承剩余寿命预测时，没有准确的划分退化状态的特征及其阈值，同时单个特征指标包含的状态信息不够全面。因此采用模糊综合评价法解决轴承振动信号的特征值难以准确划分轴承退化状态的问题，进而实现对轴承在不同退化状态下多个特征指标的剩余寿命预测。

模糊综合评价法是更加科学有效的轴承退化状态划分方法，对轴承进行退化状态划分时，首先对轴承特征指标值进行求解，进而构建隶属度函数[9]得到状态参数的隶属度，同时根据各特征指标与剩余寿命的相关系数对特征指标进行客观赋权，确定各个特征指标的权重，最后可根据轴承各状态隶属度最大原则，综合确定轴承各个状态的划分。轴承状态划分流程，如图2所示。

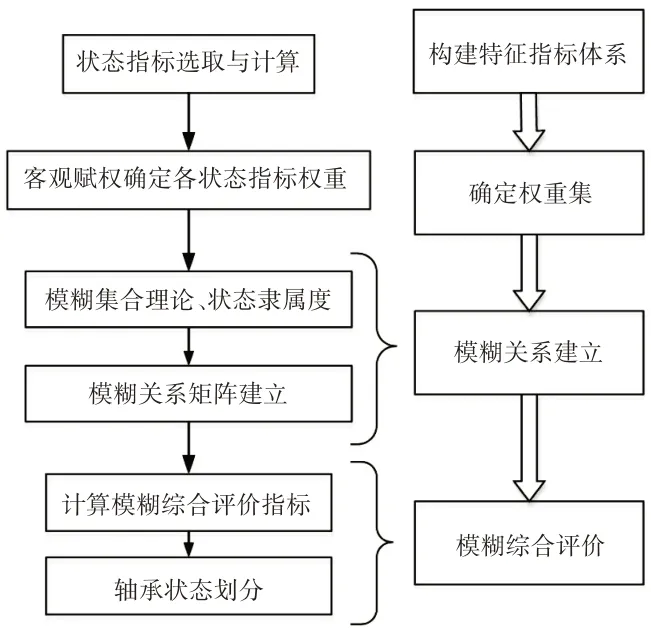
图2 轴承状态划分流程图Fig.2 Flow Chart of Bearing State Division

基于模糊评价法的轴承状态划分流程如下：构建特征指标体系。选用特征振动信号的峭度、裕度指标、频率标准差、频率均方根，作为轴承退化状态指标[10]，根据特征指标评价体系建立因素集。

构建特征指标权重集。指标权重就是各特征指标在特征指标体系中的重要性。通过比较归一化后相关系数值的大小来判断各个状态指标的相对重要程度。

建立模糊关系。模糊关系矩阵的建立是模糊综合评价的关键步骤，轴承特征指标可以用隶属度函数来描述它与退化状态之间的关系。根据轴承退化的实际情况，采用钟型隶属度函数来建立模糊关系矩阵。轴承退化状态有三种，因此所有可能的状态结果构成的评价集为V={ }V1，V2，V3=｛正常期，衰退期，快速失效期｝。特征指标因素集U和评价集V之间的模糊关系可表示为模糊关系矩阵R，即为：

（1）其中，rij=μR(ui，vj)，0≤rij≤1表示轴承在考虑特征指标ui时做出评价结果vj的概率。式中：n—特征指标体系中指标个数；m—轴承状态划分种类。

（2）模糊关系矩阵与权重集合成。模糊综合评价的结果B=[b1b2…bm]，由最大隶属度原则，可以认为该轴承特征指标处于评价结果中向量元素取值最大的状态。

根据以上采用模糊综合评判方法来划分轴承退化状态的步骤，得到状态划分结果，如图3所示。

图3 轴承退化状态划分Fig.3 Bearing Degradation State Division

分析图中各个数据样本所对应的状态类别，可以看出此图基本与图1振动信号加速度变化所对应的状态阶段一致。轴承的生命周期所经历的三种状态：在平稳磨合期，轴承的运行相对稳定，加速度幅值起伏变化较小，相对应的特征信号的变化趋势也不是很明显，此时期内轴承没有出现性能退化迹象。衰退期和失效故障期轴承的数据数量差别非常大，快速失效期的样本数据相对于衰退期的样本数据极少，为了选择出有代表性的轴承数据进行剩余寿命预测，选用处于轴承寿命周期衰退期的振动信号数据进行剩余寿命预测。

5 基于状态划分的轴承剩余寿命预测

PRONOSTIA 试验平台所采集的轴承振动信号数据包括训练集和测试集。把DE优化算法的参数设置为种群数量N=50和最大进化次数为100 次，变异算子F=0.5 和交叉概率CR=0.9。SVM回归模型惩罚因子C和RBF核函数宽度参数σ取值上下界均设置为[2−15，215]。按照DE 算法优化SVM 回归模型参数的步骤，优化结束后得出的目标函数曲线，如图4所示。在种群进化到第26代时，目标函数值MSE最小值为0.0047，最优惩罚因子C=32768，RBF核参数σ=0.1501。

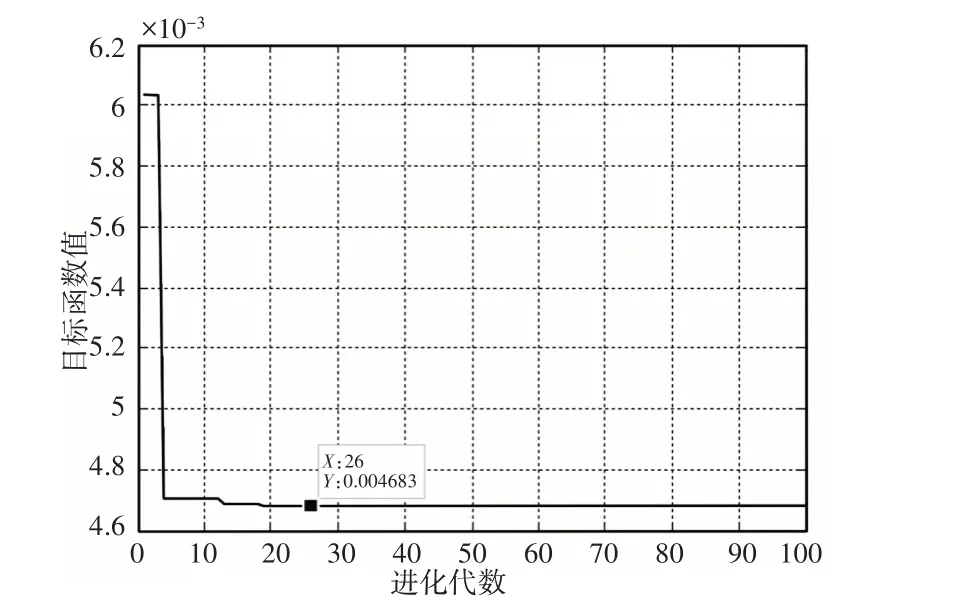
图4 DE目标函数曲线Fig.4 Curve of DE Objective Function

优化后的SVM回归模型剩余寿命预测结果，如图5所示。

图5 剩余寿命预测结果Fig.5 Residual Life Prediction Results

从图中可以看出预测值的总体变化趋势和实际值基本一致。在轴承衰退刚开始一段时间内，预测值与实际值相差的范围较大，在大约在第350个采集序列以后的中间部分的预测值很逼近真实值，在衰退后期预测值表现出较大程度地偏离真实值，此时模型的不稳定性较大。

预测结果显示平方相关系数R为0.958，说明该模型对预测数据的拟合程度较高，预测模型的MSE为0.0047，MAE为0.0490，相比较于未进行状态划分的预测结果误差，该模型的预测准确率较高，所以，该方法具有较高的可行性。

6 结论

在运用模糊综合评价方法对轴承退化状态进行模糊划分的基础上，对分状态的轴承剩余寿命进行了预测，以此来提高寿命预测的精度。通过相关分析方法选择特征集作为SVM回归预测模型的输入样本，输出样本为剩余寿命百分比，利用DE算法优化SVM回归模型参数，得到最佳的预测模型。通过分析预测结果可以看出，模糊综合评判方法可以较好地划分轴承退化状态，对预测轴承不同退化状态下的剩余寿命有利。

参看文献

［1］者娜，杨剑锋，刘文彬，等.KPCA和改进SVM在滚动轴承剩余寿命预测中的应用研究［J］.机械设计与制造，2019（11）：1−4+8.（Zhe Na，Yang Jian−feng，Liu Wen−bin，et al.Application research of KPCA and improved SVM in the prediction of rolling bearing residual life［J］.Machinery Design&Manufacture，2019（11）：1−4+8.）

［2］Kumar A，Kumar R.Time−frequency analysis and support vector ma⁃chine in automatic detection of defect from vibration signal of centrifu⁃gal pump［J］.Measurement，2017：S0263224117302750.

［3］何广坚，邢宗义，左成，等.基于EMD与SVM的城轨列车滚动轴承故障诊断方法研究［J］.铁路计算机应用，2015，24（08）：1−4+15.（He Guang−jian，Xing Zong−yi，Zuo Cheng，et al.Study on rolling bear⁃ing fault diagnosis method of urban rail train based on EMD and SVM［J］.Railway Computer Application，2015，24（8）：1−4+15.）

［4］张智胜，张云鹏，刘青.支持向量机和小波包分析下的轴承故障诊断［J］.机械设计与制造，2017（3）：204−207.（Zhang Zhi−sheng，Zhang Yun−peng，Liu Qing. Bearing fault diagnosis based on support vector machine and wavelet packet analysis［J］.Ma⁃chinery Design&Manufacture，2017（3）：204−207.）

［5］周意贺，张秀珩，王航，等.基于小波包分解与SVM的气阀故障诊断研究［J］.光电技术应用，2019，34（5）：48−52.（Zhou Yi−he，Zhang Xiu−heng，Wang Hang，et al.Study on valve fault diagnosis based on wavelet packet decomposition and SVM［J］.Photo⁃electric Technology Application，2019，34（5）：48−52.）

［6］李明，石为人.虚拟力导向差分算法的异构移动传感网络覆盖策略［J］.仪器仪表学报，2011，32（5）：1043−1050.（Li Ming，Shi Wei−ren.Heterogeneous mobile sensor network coverage strategy based on virtual force−guided differential algorithm［J］.Journal of Instrumentation，2011，32（5）：1043−1050.）

［7］傅贵，韩国强，逯峰，等.基于支持向量机回归的短时交通流预测模型［J］.华南理工大学学报：自然科学版，2013，41（9）：71−76.（Fu Gui，Han Guo−qiang，Lu Feng，et al.A short time traffic flow predic⁃tion model based on support vector machine regression［J］.Journal of South China University of Technology：Natural Science，2013，41（9）：71−76.）

［8］申中杰，陈雪峰，何正嘉，等.基于相对特征和多变量支持向量机的滚动轴承剩余寿命预测［J］.机械工程学报，2013，49（2）：183−189.（Shen Zhong−jie，Chen Xue−feng，He Zheng−jia，et al.Prediction of the remaining life of rolling bearing with relative features and multivariable support vector machines［J］.Journal of Mechanical Engineering，2013，49（2）：183−189.）

［9］韩可，姜万录，雷亚飞，等.基于变分模态分解与支持向量数据描述结合的液压泵性能退化评估方法［J］.机床与液压，2019，47（19）：164−170.（Han Ke，Jiang Wan−lu，Lei Ya−fei，et al.Evaluation method of hydrau⁃lic pump performance degradation based on variational mode decompo⁃sition and support vector data description［J］.Machine Tool and Hydrau⁃lic，2019，47（19）：164−170.）

［10］王微，胡雄，王冰，等.基于多维退化特征与GG模糊聚类的滚动轴承退化状态识别［J］.东华大学学报：自然科学版，2019，45（4）：576−582.（Wang Wei，Hu Xiong，Wang Bing，et al.Identification of rolling bearing degradation state based on multi−dimensional degradation characteris⁃tics and GG fuzzy clustering［J］.Journal of Donghua University：Natural Science，2019，45（4）：576−582.）