基于特征融合的抽油机井检泵周期预测

张晓东,王栩颖,秦子轩

(中国石油大学(华东)计算机科学与技术学院,山东 青岛 266580)

0 引 言

随着石油工业的不断发展，有杆抽油机在石油工业中得到了大力发展和广泛应用，抽油机井故障成为严重影响油田生产的问题之一[1]。由于井下的工作环境复杂，抽油设备受疲劳、磨损、腐蚀等多因素影响容易发生故障，导致检泵，因此有效预测故障，确立合理的检泵周期，有助于提高油田的生产效率和经济效益。研究人员在抽油机井故障预测及检泵周期预测等方面做了大量的研究工作[2-9]。

目前的研究多采用线性回归和概率分布方法研究环境因素对检泵周期的影响规律，文献[2]则通过回归分析的方法，阐述了针对存在杆管偏磨现象的抽油机井检泵周期与其影响因素间定量的相互作用；分别构建了冲程、冲次、回采工作面液量、含水率变化规律与检泵周期的一元回归表达式,并构建了多种因素影响联合效应与检泵周期变化的多元回归表达式。研究结论在一定程度上体现了主要人为调节因素对杆管偏磨失效现象的影响规律。文献[3]根据油田抽油机井没有确定的故障发生率函数和最佳预防性检泵周期变化和检泵策略，提出了基于威布尔分布的抽油机井事故发生率研究。通过分析检泵周数据，建立了分布模型并使用模糊粒子群—模拟退火算法，对分布模型进行了参数化计算并定义了机采井故障率函数，以及利用模糊决策分析法估算最佳的检泵周期。文献[4]通过分析实际油井检泵作业数据，使用概率分布模型描述了检泵周期与设备失效风险的分布规律，使用三参数威布尔分布模型，描述了检泵周期与泵可靠度的相关关系，并建立了某一固定时间区间内检泵作业井数的概率预测模型。

有杆抽油机井由抽油杆、抽油管、抽油泵以及井下配套工具4个部分组成，通常把各部分的最短寿命作为检泵周期，对各部分设备进行动力学分析，预测检泵周期。文献[5]基于GA-SVM和蒙特卡罗模拟建立了抽油杆磨损分析与安全评估模型。分析抽油杆受力情况,建立了井下影响因素与抽油杆磨损率的映射关系，预测抽油杆的寿命。文献[6]针对水平井在复杂受力环境下井下扶正器疲劳导致故障的情况，运用ANSYS对扶正器进行了力学分析和疲劳寿命分析，研究建立了水平井抽油杆扶正器的仿真模型，并模拟了扶正器工作的受力情况，认为传统的扶正器结构存在应力集中现象，并提出了结构优化方案。文献[7]将壁厚值、直径和缺陷尺寸等参数作为疲劳寿命模型计算输入参数，利用在线检测技术和疲劳寿命相结合的评价方法，更加准确预测剩余寿命。文献[8]使用深度学习方法中的长短时记忆网络(Long Short-Term Memory, LSTM),根据已有的油田生产数据,选取了15项与抽油杆腐蚀密切相关的变量,通过参数优化、网络训练,构建了基于LSTM的抽油杆剩余寿命预测模型。文献[9]提出了基于灰度矩阵极限学习机(Gray Matrix-Extreme Learning Machine, GM-ELM)的故障诊断方法，利用灰度矩阵对有杆抽油机井进行故障特征提取，再采用数理统计的方式建立灰度矩阵的特征向量，将故障特性向量作为故障诊断模式的输入值，通过构建GM-ELM模式对抽油机井故障进行检测。

目前基于回归分析的油井检泵周期的预测方法均为纯数学的方法，缺少理论依据，且精度较差；对设备的寿命预测大多没有形成量化模型，影响因素考虑不全面，对油井检泵计划缺少指导性。以上方法有待于进一步完善和深入研究。本文利用支持向量机回归与卷积神经网络，根据抽油机井生产参数的特点，分别提取检泵周期相关参数的静态特征和动态特征，通过多模态压缩双线性池化融合特征向量，基于判别模型建立检泵周期预测模型，可进一步提高预测的准确率。

1 基于特征融合的检泵周期预测模型

根据抽油机井生产数据的性质，将影响检泵周期的参数分为静态参数和动态参数。静态参数是指抽油机井工作状态数据，表征物理状态，每月更新，且变化较小；动态参数是指抽油机井生产数据，与油井的运行相关，每天都会产生新数据。考虑到2类参数特征不同，分别对静态参数和动态参数建立特征提取模型，将提取出的2类特征输入多模态压缩双线性池化模型进行特征融合，利用判别模型对融合特征进行重学习预测抽油机井检泵周期，如图1所示。

图1 模型框架

针对静态参数变化不大且数据量小的特点，采用SVR建立静态特征提取模型；动态参数的数据量较大，采用卷积神经网络提取动态参数特征。

1.1 静态特征提取模型

1.1.1 静态参数筛选

抽油机井的静态参数表征井的物理状态，正常工作情况下，数据变化较小，采用Spearman秩相关系数[10]，计算预静态参数与检泵周期的相关程度大小来分析影响检泵周期的主要因素。Spearman秩相关系数是利用单调方程衡量2个变量的依赖性的非参数指标，即便在变量值没有变化的情况下，也不会出现像Pearson相关系数分母为0而无法计算的情况。Spearman秩相关系数如下：

(1)

其中，di表示2个变量分别排序后成对的变量位置差，n表示样本数量。分别以上行电流、下行电流、泵径、泵深、冲程、冲次、排量、泵效、含水率、载荷差为分量组成变量M，以检泵周期天数为因变量N，di为M、N的秩次之差，分别计算各参数的r值，结果如表1所示。

表1 Spearman相关系数r值

表1中的数据是基于某油田10年内近8000口抽油机井的生产作业数据集计算得出，r值表示静态参数与检泵周期的相关系数值，r值越大表示相关性越高。分别选取r值大于0.5的7种参数、r值大于0.6的6种参数、r值大于0.7的5种参数作为静态参数，将3组静态参数进行特征提取、特征融合之后，输入判别模型预测检泵周期，预测准确率分别为0.78、0.83、0.71。同时根据机理分析，泵效是指在抽油井生产过程中，实际产量与理论产量的比值，对造成抽油机井的故障因素影响不大。

综合实验结果与机理分析，从表1中筛选r值大于0.6的静态参数作为模型的输入参数，包括泵深、冲程、载荷差、冲次、含水率、泵径。

1.1.2 静态参数提取

支持向量机回归(SVR)[11-13]本质上是利用一种非线性映射,把不能线性返回的样本数据映射到更高维度实现线性返回，该回归的函数表达式为：

f(x)=ωTφ(x)+b

(2)

基于SVR的静态特征提取模型的过程描述如下：

1)构建训练样本。

2)获取最优的惩罚因子和核函数宽度。

惩罚因子C用来调节模型复杂度与经验误差之间的平衡，核函数宽度σ影响特征空间中样本数据分布的复杂程度。SVR的回归性能与核函数有关，径向基核函数(Radial Basis Function, RBF)[14]计算量较小且计算效率高，使得模型具有更强的泛化能力和学习能力，径向基核函数如下：

(3)

选取径向基核函数，将(C,σ)初始化，采用网格搜索法，设置选择范围、终止条件以及网格搜索步长，在所有的(C,σ)组合内引用SVR对样本进行学习，计算结果使用交叉验证均方差(MSE)表示：

(4)

其中，yi为训练集输出值，即第i个点的实际检泵周期误差，y′i为第i个点的预测值。计算MSE，MSE值越小，(C,σ)参数组合效果更好。

3)训练模型。

将训练样本和最佳的(C,σ)参数组合代入SVR模型进行训练，根据样本数量N和检泵周期值拟合每个输入的权重ω，将静态参数输入训练好的模型中提取静态参数特征。

1.2 动态特征提取模型

1.2.1 动态参数筛选

抽油机井每天都会产生新的动态参数数据，数据量十分庞大，采用Pearson相关系数[15]筛选动态参数中与检泵周期相关性强的参数，其输出范围为[-1,1]，正值表示正相关，负值表示负相关，0表示无相关性。将检泵周期作为特征向量，使用Pearson相关系数分析各动态参数与检泵周期的线性关系绝对值大小，输出值的绝对值越大，则相关性越强。Pearson相关系数观测值X、Y的总体相关系数为：

(5)

其中，cov(X,Y)用于表示X、Y特征的协方差，σX为X特征的标准差，σY则主要用于表示Y特征的标准差。

分别以日产液量、日产油量、日产水量、油压、套压、流压、动液面、井口温度为分量组成X={x1,x2,…，xi}，xi为某一天的参数值，以检泵周期为Y={y1,y2,…,yi}，yi为xi对应的检泵周期天数，计算Pearson相关系数公式rxy：

(6)

由此可以得到检泵周期与各生产参数的Pearson相关系数r值，如表2所示，样本数据为某油田近10年的生产数据。

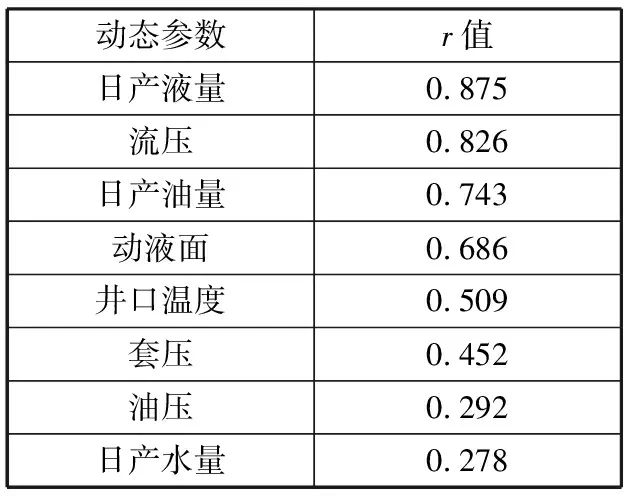
表2 Pearson相关系数r值

分别选取r值大于0.4的6种参数、r值大于0.5的5种参数、r值大于0.6的4种参数作为动态参数，将3组动态参数进行特征提取、特征融合之后，输入判别模型预测检泵周期，预测准确率分别为0.75、0.86、0.80。并且根据实际生产经验，井口温度会影响原油粘度，对抽油杆的作用力有较大影响，相对于粘度来说，套压和油压的影响较小。综合实验结果与机理分析，从表2中筛选r值大于0.5的生产参数作为输入特征，包括日产液量、流压、日产油量、动液面、井口温度。

1.2.2 动态特征重建

在训练模型之前，为防止数据中存在较大数值的数据影响数值较小的数据对于训练的效果，需要对数据进行标准化、归一化操作消除量纲。表达公式如下：

(7)

卷积神经网络的输入为矩阵，由于动态参数种类较少，要将参数结构进行重建。以单个井为例，按时间顺序选择5种动态参数的30条数据作为一组，将6组数据合并为一个30×30的矩阵。

1.2.3 动态特征提取

将重建后的动态参数输入到卷积神经网络(Convolutional Neural Networks, CNN)[16-18]中进行训练，深层卷积神经网络能够更好地提取不同参数的特征信息，模型泛化能力强，但随着网络深度加深会出现梯度消失或梯度爆炸现象。残差网络(Residual Network, ResNet)[19-21]通过捷径连接和恒等映射组成的残差块，使得网络深度增加时模型不退化，具有更强的特征提取能力。

本文采用的ResNet-50整体结构如图2所示，首先通过Stage1的7×7卷积层和3×3最大池化层对输入数据进行一次特征提取操作，再通过Stage2中的4个残差结构提取更高层特征信息，最后通过Stage3全连接层输出提取后的动态特征。

图2中Conv是卷积层，Batch Norm表示批量正则化处理，Max Pool表示最大池化操作，Avg Pool表示平均池化操作。激活函数选择线性整流单元ReLU函数[22]，表达式如下：

图2 ResNet-50网络结构

f(x)=max(0,x)

(8)

其中，线性整流单元的输入为x，同时也是上一层的网络输出，x与0的相对极大值就是线性整流单元的输出结果。

1.3 特征融合

由于从静态参数中提取的静态特征和从动态参数提取的动态特征分别表示单方面的特征，不能单独预测检泵周期，所以需要将2类特征进行特征融合，将融合后的特征向量作为输入，预测检泵周期。将提取的静态特征记为f1(Sn)和动态特征记为f2(Dn)，输入多模态压缩双线性池化(Multimodal Compact Bilinear Pooling, MCPB)模型[23]进行特征融合。由于MCBP采用外积的计算方法，融合了静态特征f1(Sn)和动态特征f2(Dn)特征向量中每个元素之间的相互关系，所产生的多模态融合特征向量更具表达性；并且MCBP将静态特征f1(Sn)和动态特征f2(Dn)特征向量投射到频域空间，无需直接计算外积，避免了计算复杂、容易产生过拟合等问题。

MCBP采用Count Sketch投射函数ψ，将静态特征向量和动态特征向量的外积f1(Sn)⊗f2(Dn)投射到低维空间表示为：

ψ(f1(Sn)⊗f1(Dn),h,g)=ψ(f1(Sn),h,g)*ψ(f2(Dn),h,g)

(9)

其中，h、g为哈希映射，*表示卷积运算。根据卷积定理，时域中的卷积对应频域中的乘积，式(9)可表达为：

ψ(f1(Sn)⊗f1(Dn),h,g)=FFT-1(FFT(f1′(Sn))⊙f2′(Dn))

(10)

其中，⊙表示点积操作，结果为融合后的特征向量。

1.4 判别模型

为提升检泵周期预测的准确率，本文提出3种判别模型，分别为基于GMM的判别模型、基于决策树的判别模型和基于线性模型的判别模型，用3种判别模型分别预测检泵周期，验证哪种模型对于检泵周期预测的效果更好。将判别模型训练的损失函数定义为：

(11)

其中：Pi表示判别模型输出的预测检泵周期值；Yi为实际检泵周期值。

1.4.1 基于GMM的判别模型

高斯混合模型(Gaussian Mixture Model, GMM)[24]是一种基于概率模型的聚类方法，假设输入样本服从k个参数未知的高斯分布，服从同一分布的样本则被聚为一类。利用高斯混合模型的检泵周期预测过程如下：

1)最优聚类个数。

为较准确地预测检泵周期，缩小天数范围，依据实际生产经验及数据，将检泵周期天数300～1200天，分别按照间隔50天和100天进行分组，可分为18类和9类。利用贝叶斯信息准则(Bayesian information criterion, BIC)[25]的模型选择理论对上述2种分组进行概率估计。表达式为：

CBIC=-ln(L)+npln(m)

(12)

其中，CBIC为BIC值，np为超参数的个数，L为模型估计似然函数的最大值。计算结果如表3所示，以具有低BIC值的模型为优。

表3 2种分组的BIC值

由表3结果可知，当聚类个数为9时的CBIC值更小，因此按照间隔100天对检泵周期进行分组。

2)聚类检泵周期。

将融合后的特征向量输入高斯混合模型进行训练。利用最大期望(expectation-maximization, EM)算法[26]对k个混合的高斯分布进行拟合，以求得每个分布的均值μj和协方差εj(1≤j≤k)。利用计算获得的高斯参数，遍历所有样本，将样本归于概率最大的一类。

1.4.2 基于决策树的判别模型

梯度提升迭代决策树(Gradient Boosting Decision Tree, GDBT)[27]是Boosting算法中的一种，是决策树(CART)的加法模型，核心在于累加所有树的结果作为最终结果。在预测检泵周期时，将损失函数的负梯度在当前模型的值，作为残差的近似值去拟合一个回归树得到最终的回归树：

(13)

XGBoost[28-30]是对GDBT的改进，在最小化损失函数时进行了正则化，拟合上一轮强学习器损失函数的二阶导展开，提高了精度。对于目标函数，使用二阶泰勒展开式来优化，目标函数为：

(14)

1.4.3 基于线性模型的判别模型

逻辑回归(Logistic Regression, LR)[31-33]是一种广义的线性回归分析模型，主要思想是在线性回归的基础上，通过Sigmoid函数引入非线性模型，逻辑回归模型表达为:

z=θTX

(15)

其中，X为静态特征与动态特征融合后的特征向量，θT为回归系数。使用Sigmoid函数作为预测函数，表达式为：

(16)

采用最大似然估计法对回归系数进行估计，损失函数最小时，求得最佳回归系数值，代入模型，预测检泵周期。

2 实验分析

2.1 数据集

实验数据集来源于某油田的抽油机井生产数据，将与抽油机井检泵周期相关的参数按照类型分为静态参数和动态参数，静态参数主要包括上行电流、下行电流、泵径、泵深、冲程、冲次、排量、泵效、含水率、载荷差，动态参数主要包括日产液量、日产油量、日产水量、含水率、油压、套压、流压、动液面、井口温度等。

将数据集随机划分，70%的数据用于训练，30%的数据用于测试。在训练阶段，首先对数据进行预处理，分别提取静态数据和动态数据的特征，再利用多模态压缩双线性池化融合2类特征，将融合后的特征向量输入判别模型进行训练。在测试阶段，将测试数据输入训练好的判别模型，最终预测抽油机井检泵周期天数。

本文设计2个指标去评价模型。一是计算模型预测的检泵周期天数和真实检泵周期天数的均方根误差(Root Mean Square Error， RMSE),表示模型预测的误差,计算公式为：

(17)

二是计算模型准确率衡量模型预测的有效性，预测结果|Pj-Yj|≤0.1×Yj表示预测准确，其中Pj表示预测的检泵周期值，Yj为实际检泵周期值；否则表示预测不准确。

2.2 实验结果和分析

针对本文的检泵周期预测模型，从以下3个方面对该模型进行有效性分析：1)分析模型本身参数对于模型的影响；2)使用不同的判别模型分析对预测结果的影响；3)使用其他故障预测的方法与本文的模型进行对比验证。

静态特征提取模型中的核函数将特征从低维到高维进行转换，分别使用了多项式核函数、径向基核函数和线性核函数，分析不同的核函数对于静态特征提取的影响，其中模型参数C=4，ε=0.274，σSVR=0.047；对于动态特征提取模型，分别使用了vgg16、vgg19、resnet34和resnet50等卷积神经网络，分析了不同的算法对动态特征提取的效果。如表4所示，resnet的预测结果明显优于vgg，残差这一结构可以更好地帮助模型进行预测，而通过径向基核函数将数据进行高维映射可以更好地提取静态特征。

表4 特征提取模型结果

本文对比了5种不同的动态特征提取网络，分析了网络中不同的结构对模型效果的影响，如表5所示，模型A是基础的网络，模型B用了更简单的全连接层，模型C用了2个更小的卷积核代替模型A中的大卷积核，模型D用了更多的卷积层和更少的全连接层，模型E相比模型C则是增加了全连接层的宽度。如表6所示，模型A和模型C取得了更好的预测结果，更大的全连接层可以获得更好的预测结果，而卷积层对于预测结果影响并不大。

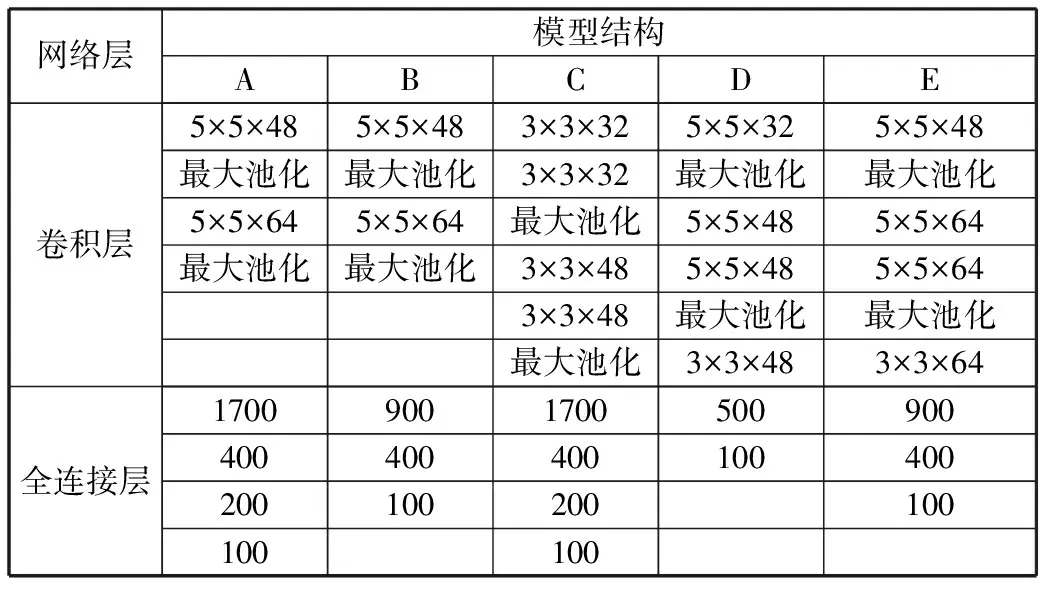
表5 模型结构

表6 模型预测结果

判别模型将融合之后动态特征和静态特征映射至检泵周期，实现最终的预测过程，选择较为契合油井数据特点的判别模型可以极大地提高模型的准确性，本文使用了GMM、逻辑回归、GBDT以及XGBoost等4种不同的判别模型分别对检泵周期进行预测，如表7所示，由于数据特征较为混乱，难以聚类，故GMM的表现效果最差；数据量不足导致了逻辑回归的预测结果也难以取得理想结果；而GBDT和XGBoost取得了较好的结果。

随机抽取40口测试集中的抽油机井进行预测并显示检泵周期预测值和真实值的对比图，具体分析模型的有效性，如图3所示，模型预测的检泵周期值可以较好地拟合真实值，在一定程度上可以为检泵作业进行指导作用。

图3 检泵周期预测结果

对比文献[9]中基于GM-ELM的有杆泵抽油井故障诊断方法(模型A)和文献[34]中基于LSTM循环神经网络的故障时间序列预测方法(模型B)与本文的基于特征融合的检泵周期预测方法(模型C)进行对比。预测结果如表8所示，由于模型B对于油井数据并不是专门契合，其预测准确性较差；而本文模型根据油井数据的特点将其进行分类并设计不同的模型处理不同类型的数据，故得到了较好的预测结果。

表8 模型预测结果对比

3 结束语

针对石油生产中抽油机井检泵周期的问题，本文提出了基于特征融合的检泵周期预测模型。输入抽油机井历史生产数据和作业数据，采用径向基核函数的SVR算法提取静态参数特征，采用卷积神经网络进行动态特征提取，利用多模态压缩双线性池化模型将静态特征和动态特征进行特征融合，并基于判别模型方法构建检泵周期预测模型。采用生成的测试集对优化后的预测模型进行测试，模型预测的准确率达到了89%，综合性能优于其他模型。本文所提出的抽油机井检泵周期预测方法对指导油田生产作业具有一定参考价值。