基于大规模MIMO的散射信道估计技术
2022-12-30史清林刘丽哲李行健
史清林,刘丽哲,李行健
(中国电子科技集团公司第五十四研究所,河北 石家庄 050081)
0 引 言
数字化战场要求信息传输具备更高的速度,但带宽资源是有限的,这意味着所使用的通信技术应具备更高的频谱效率。对流层散射通信是一种重要的军事通信和应急保障通信手段。虽然该技术可靠性高、单跳距离远、保密性强,但通信链路的路径损耗大,信号衰落严重,频谱效率不高[1]。
目前,学界正在开展大容量散射技术的研究,大规模MIMO技术是提升通信系统频谱效率的可行手段[2]。现阶段的散射通信系统采用传统MIMO技术,天线配置为2×2,不仅分集重数低,也不具备复用功能[3]。在散射通信中引入大规模MIMO技术,使得系统的空间利用率、数据传输速率、频谱效率获得提升[4]。在大规模MIMO系统下,接收端的信号检测[5]、功率分配[6]、预编码设计[7]都需要用到信道状态信息(Channel State Information, CSI),CSI可以通过信道估计来获取。信道估计方法可以分为3类:盲信道估计[8]、半盲信道估计[9]和导频辅助的信道估计[10]。盲信道和半盲信道估计方法,不需要过多的时间开销来估计信道,但在信道快衰落的场景下难以实现精确的信道估计。对于导频辅助的信道估计而言,导频信号估计的CSI在相干时间内可视为恒定,用于对接收信号的后续操作。目前,在散射通信中较为常用的导频辅助信道估计方法有:LS信道估计方法[11]、MMSE信道估计方法[12]。LS信道估计方法虽然简单但结果并不准确;MMSE信道估计方法虽然准确但需要难以获得的信道先验信息。在大规模MIMO散射通信系统下,由于天线数量增长,信道估计处理的复杂程度急剧增加[13]。这使得传统的信道估计算法效果变差,需要针对使用场景建立合适的信道模型并研究更加有效的信道估计算法。
2017年,韩国中央大学的Jingon Joung团队在文献[14]中推导出空间相关的瑞利衰落信道的协方差矩阵,论证了协方差矩阵、收发天线的相关因子及多径时延扩展的关系,旨在更加准确地估计CSI并降低反馈开销。2018年,阿肯色大学的Aqiel Almamori团队在文献[15]中提出了一种估计信道相关矩阵的新方法,利用预测的相关矩阵估计MMSE所需的信道先验信息,此方法对配备ULA的大规模MIMO信道的估计准确度接近理想的MMSE算法。2020年,都柏林城市大学的Sidharth Mohanty团队在文献[16]中研究了天线数为20~500的大规模MIMO系统在具有加性高斯白噪声的瑞利衰落信道下的误码率性能,探索了大规模MIMO系统在完全和不完全CSI下克服多径衰落和支持多用户通信的能力。2021年,伦敦玛丽女王大学的Kangda Zhi团队在文献[17]中构建了可重构智能曲面(RIS)辅助的大规模MIMO系统,并对该系统的CSI统计特征进行了分析和估计。针对大规模MIMO由于信道老化、导频污染、系统吞吐量受限引起CSI估计不准确的问题,高通公司的Vikas Arya团队在文献[18]中将随着用户移动而变化的平均总传输速率和大量的历史样本用于CSI的估计,提升了干扰下大规模MIMO系统信道估计的准确性。这些国际研究为大规模MIMO信道估计提供了新的研究思路,在研究中更加关注收发天线的相关性及信道协方差矩阵的影响。同时,他们将大规模MIMO系统与IRS、抗干扰技术相结合,为该领域的信道估计提供了更加丰富的应用场景。但是,目前学界主要针对基于ULA的大规模MIMO移动通信系统的信道估计方法进行研究,对配备URA的大规模MIMO散射通信系统的信道估计方法研究较少。同时,在信道协方差阵的估计方面,学界的科研成果主要集中于由ULA构成的通信场景,对由URA构成的通信场景研究较少。
因此,本文创新点在于:建立配备二维均匀方形天线阵列(Uniform Rectangular Array, URA)的大规模MIMO散射通信系统信道模型;利用URA自相关矩阵的特性估计信道协方差矩阵,提出一种针对URA场景的信道协方差阵估计算法;通过该算法,提出准确度逼近理想MMSE算法的改进MMSE信道估计算法。
1 信道建模
本文研究的大规模MIMO对流层散射通信系统模型如图1所示,散射通信站A、B可以通过对流层中的散射体进行超视距通信。A、B这2站装配的天线阵列为URA,各阵元为正方形,相邻阵元间距相同,可设置为数十个波长。阵元序号从左到右、从上到下依次递增,总数为16的阵元布置如图2所示。
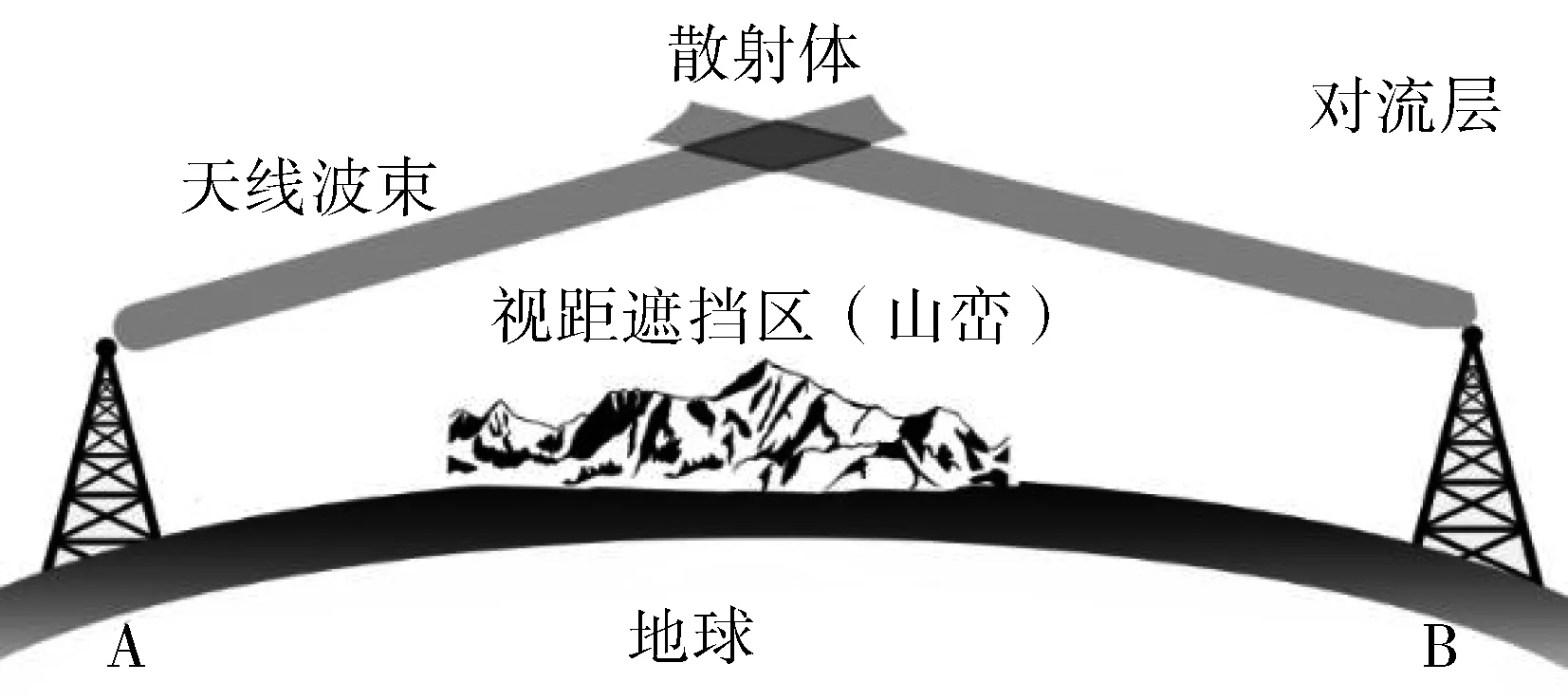
图1 大规模MIMO散射系统示意图

图2 二维天线阵元布置图
在大规模MIMO通信系统中,信道矩阵H为:
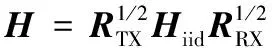
(1)
其中,RTX、RRX分别为发送端、接收端的相关矩阵,Hiid为不含空间相关性的多径信道矩阵。
散射信道具有显著的多径效应,信号经历小尺度衰落[19]。文献[20]中通过相关法对散射信道进行分析,得出如下结论:散射信道最多有效径数为5径,最大多径时延扩展不超过0.4 μs,最大多普勒频移为5~6 Hz左右。文献[21]中利用散射信道综合测试设备,对多条实际链路进行测量,得出如下结论:相关带宽为3.5 MHz,最大多径时延扩展为0.45 μs。文献[22]指出工程中普遍使用的7径信道模型对于研究和表征散射信道已经足够。因此,本文选择7径模型模拟散射信道。
在相关矩阵模型的选取上,传统的相关矩阵模型并不具备相邻天线的相关性高于遥远天线的实际信道特征。目前,学界提出的指数相关模型[23]已成功地应用于包括大规模MIMO[24]在内的许多通信问题。文献[25]从数学上证明了指数相关模型的有效性。该模型具备物理上的合理性,其相关性随着接收天线之间距离的增加而指数性地减小,这与现实的物理环境相对应。因此,本文将采用指数相关模型模拟收发天线阵元间的相关性。
1.1 7径信道模型
本文采用文献[26]的7径信道模型数据,如表1所示。由于最大多普勒频移很小,不再考虑多普勒频移的影响。随后,通过抽头延迟线模型(Tapped Delay Line, TDL)来产生空间不相关的对流层散射衰落信道,TDL时域模型如图3所示。
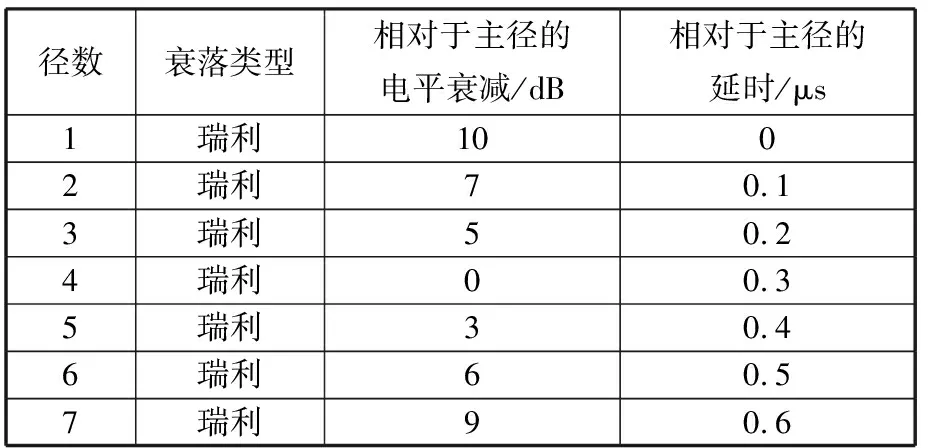
表1 7径模型参数配置表
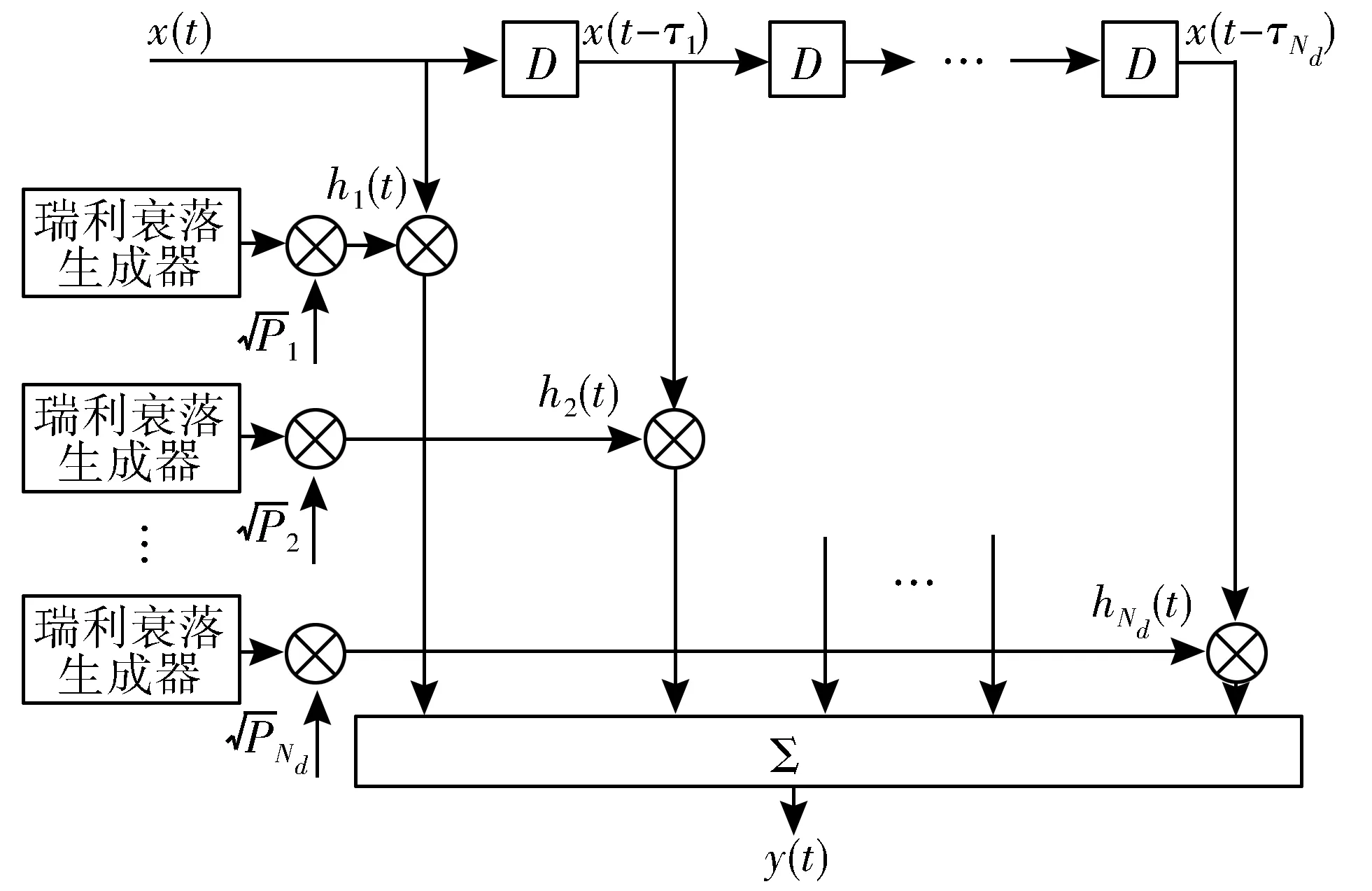
图3 TDL模型
在TDL中,瑞利衰落生成器生成复高斯变量h0(t)~CN(0,1),h0(t)与各径功率的平方根相乘后,获得该径的信道系数。TDL在时域上的表达式如下:
(2)
其中,x(t)为发送信号,y(t)为接收信号,hi(t)为第i条径的信道系数,τi为第i条径的时延,Nd为最大径数,Pi为第i条径的功率。
根据傅里叶变换的时移性质[27],TDL在频域的表达式如下:
(3)
其中,f为载波频率。
对于收发端天线阵元数目分别为Nt、Nr的大规模MIMO对流层散射单载波通信系统,信道为窄带平坦衰落,在频域上由TDL生成不含空间相关性的7径信道矩阵如式(4)所示:
(4)
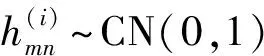
1.2 指数相关模型
URA相较于一维均匀线性阵列(Uniform Linear Array, ULA)空间利用率高,在总速率相同时,URA只需要ULA宽度的30%~50%[25]。在相同的空间资源下,URA比ULA的部署更加紧凑、传输数据速率更高。假设A、B两端天线结构及架设周围的电磁环境完全相同,故收发双端相关矩阵相等。由文献[28]可以得出基于URA的大规模MIMO的指数相关模型如下:
(5)
其中α∈(0,1)可由实际测量获得;di,j表示序号i、j的阵元间距。
由文献[29]可知在大规模MIMO通信系统中,信道的空间相关矩阵为:
R=RTX⊗RRX
(6)
其中,⊗表示Kronecker积。
2 信道估计
2.1 系统模型
本文建立的系统模型如式(7)所示:
Y=HX+W
(7)
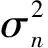
在所建立的模型中,发送导频信号XP用来估计信道,XP如式(8)所示:
(8)
其中,发送端天线数目为Nt,则导频长度L≥Nt。为了便于分析,本文令L=Nt。当需要L>Nt时,可以增加重复导频或者用0作为循环前缀(Cyclic Prefix, CP)填充到导频中。
将多次测量的接收信号收集并向量化后,得到:
(9)
2.2 信道估计算法
在信道估计算法中,LS算法和MMSE算法各具优势,因此通常与其它的信道估计方法相比较来衡量其它信道估计方法的性能。LS算法实现简单、准确度较低,通常作为衡量信道估计方法准确度的下界。MMSE算法需要信道协方差矩阵进行运算,而信道协方差矩阵作为信道先验信息是未知的。在实际应用中,MMSE算法使用的是信道协方差矩阵的估计值。因此,MMSE算法的准确度与信道协方差阵的估计值准确度有关。文献[30]根据最大似然原理,采用时隙平均信道协方差阵估计方法的MMSE算法,其协方差阵是通过一段时隙接收的导频信号自相关阵进行估计,其准确度比LS算法要高。为叙述方便,本文将基于时隙平均的信道协方差阵估计方法的MMSE算法记作传统MMSE算法。当采用真实的信道协方差矩阵时,MMSE算法的准确度获得最大提升,此时称为理想MMSE算法。理想MMSE算法的准确度明显优于LS算法、传统MMSE算法,通常作为衡量信道估计方法准确度的上界。
由于时隙平均的信道协方差矩阵估计方法不具有对信道模型特征的针对性,导致信道估计不够准确。并且,该方法基于最大似然原理对信道协方差阵进行估计,需要大量时隙样本才能提升估计精度,而一个时隙所取得的样本数量有限,这也导致信道估计不够准确。因此,本节针对URA的排布特点分析信道协方差矩阵的结构特征,将信道协方差矩阵的估计问题转化为参数估计问题,对传统MMSE算法的信道协方差阵估计方法进行了改进,利用改进的信道协方差阵估计算法恢复出精确的信道协方差阵,只需有限的时隙样本就可以更加准确地估计信道。
2.2.1 LS算法
LS信道估计方法的目标函数[31]为:
(10)
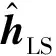
(11)
LS估计量与真实值之间的均方误差为:
(12)
2.2.2 MMSE算法
MMSE估计方法的目标函数[32]为:
(13)
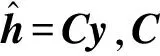
(14)
MMSE估计值与真实值之间的均方误差为:
(15)
LS的估计误差与MMSE的估计误差相比,得到:
(16)
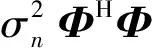
由此可见,信道的协方差矩阵Rh作为信道的统计信息在信道估计中扮演了重要的角色,提升了信道估计的准确性。
2.2.3 改进的信道协方差阵估计算法
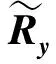
(17)
(18)
(19)
(20)
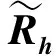
信道协方差矩阵Rh与相关矩阵R的关系如式(21)所示,可以注意到前者是后者的β倍。通过观察R的结构特征,可以发现R仅存在1个待估计参数α。因此,对信道协方差矩阵的估计可以转化为对α和β的估计。由于α∈(0,1),R中的元素αdi,j大小随着其指数di,j的增大而变小,其位置分布也因Kronecker积运算而具有一定的规律性。以Nt=Nr=4为例,其阵元布置如图4所示。其RTX和RRX如式(22)所示,d0表示阵元间的最小距离。
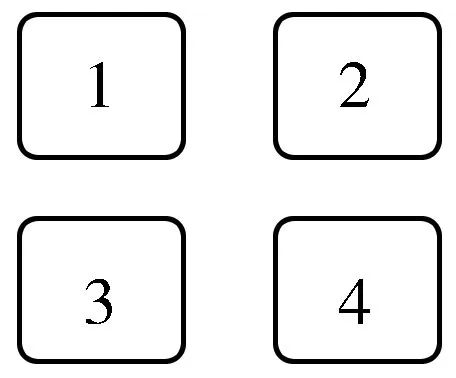
图4 阵元数为4时阵元布置
(21)
(22)
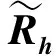
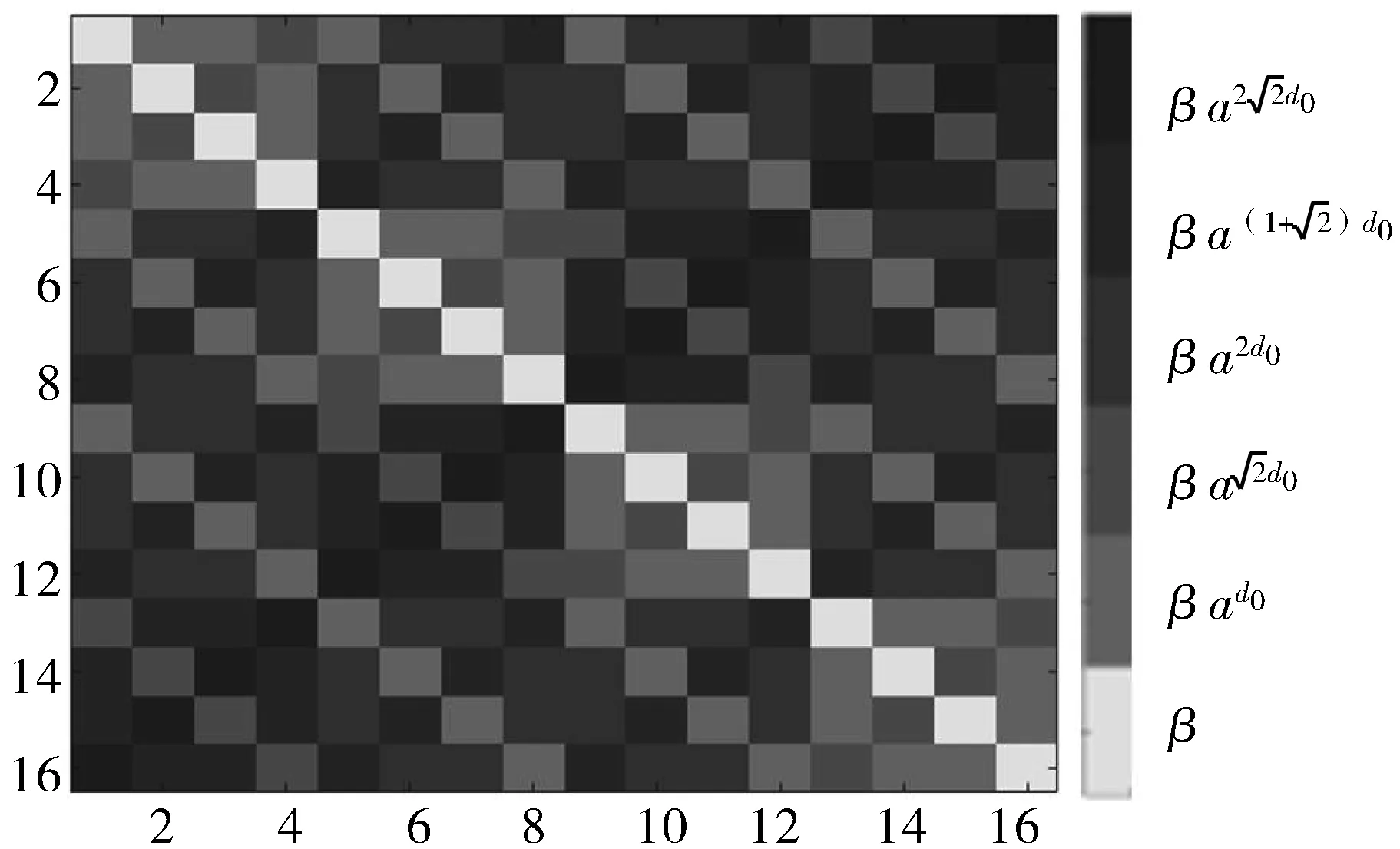
图5 阵元数目为4时Rh的结构
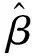
(23)
(24)
其中,N为R中αd0元素的总数,(in,jn)表示第n个αd0位置坐标。
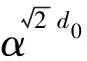
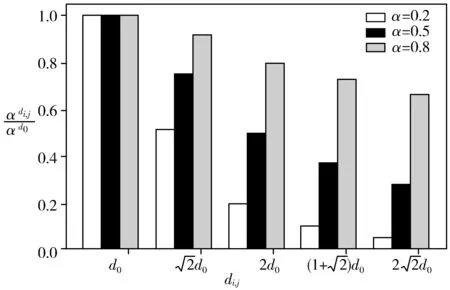
图6 不同α时Rh各位置元素对比
算法1改进的信道协方差矩阵估计
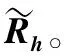
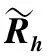
获得改进MMSE估计值的公式为:
(25)
噪声水平σn2和信道的协方差矩阵Rh作为信道的先验信息,其获得具有相当大的难度。但与信道本身的快衰落不同,这2个统计值都是随机变量的二阶统计量,其随时间变化速度很慢。因此本方法可以利用一段时间内接收到的含有噪声的导频信号来估计信道的协方差矩阵,而噪声水平σn2可以通过静默信号或CP进行估计。
3 仿真分析
本章将式(25)所示的改进MMSE算法与3种算法的准确度进行比较,分别为:式(11)所示的LS算法[31]、式(14)所示的理想MMSE算法[32]、式(20)所示的基于时隙平均估计协方差阵的MMSE算法[30]。为了便于区分,在仿真结果中将基于时隙平均估计协方差阵的MMSE算法记作传统MMSE算法。由于Rh是真实的信道协方差矩阵,理想MMSE算法的估计精度为其它算法提供了上界。
3.1 仿真参数
仿真参数如表2所示,由于在理论上任何可逆矩阵都可以作为导频矩阵,为便于分析,XP使用单位矩阵,表示每次只有一个天线发送信号。
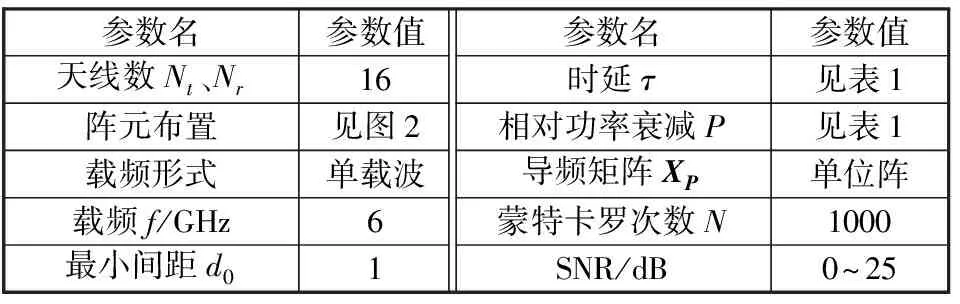
表2 仿真参数配置表
在此类信道估计中,导频矩阵XP和导频信号y是已知的,需要从矩阵Φ和向量y中估计信道向量h。不同信道估计方法的准确度可以通过NMSE准则评定,NMSE准则如下:
(26)
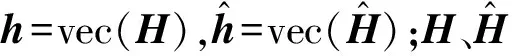
3.2 结果分析与比较
在SNR为0~25 dB的条件下,采用LS和理想MMSE算法对α为0、0.2、0.5和0.8的大规模MIMO对流层散射信道的估计准确度进行比较,结果如图7所示。从横向上观察可知:在空间相关性相同时,理想MMSE算法的准确度优于LS算法,在SNR为0~10 dB范围内优势更加明显。在α为0.8、NMSE为-8 dB时,理想MMSE算法的SNR比LS算法提升7 dB左右,随着信噪比的增大,2种算法的准确度趋于一致。从纵向上观察可知:随着信道相关性的增强,理想MMSE算法准确度提高。在SNR为5 dB的条件下,理想MMSE算法在α为0.8时比α为0时准确4 dB左右,而LS算法准确度变化不大。
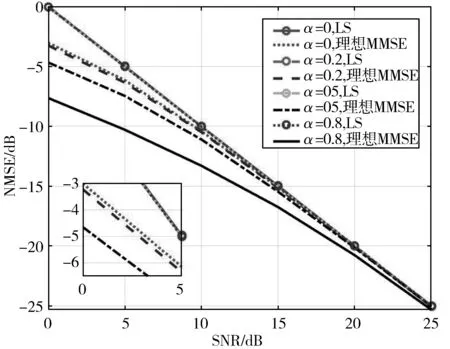
图7 LS和理想MMSE方法的NMSE曲线
当收发天线阵元数均为16时,其信道协方差阵的βαd0位置如图8中浅色方格所示。在α为0、0.2、0.5和0.8的信道情况下,对比LS、理想MMSE、传统MMSE及改进MMSE算法在SNR为0~25 dB内的准确度,如图9~图12所示。
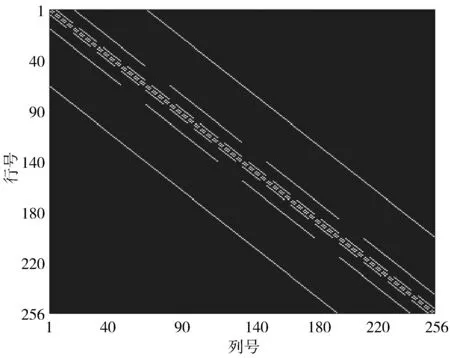
图8 信道协方差阵中βαd0的位置分布
从图9中可以看出,在α为0即收发天线阵元间相互独立时,改进MMSE算法比MMSE算法的准确度有明显的提升。在NMSE为-4 dB时,传统MMSE算法的SNR比LS算法提升0.1 dB,但比理想MMSE算法差2.1 dB,改进MMSE算法的SNR与理想MMSE算法仅相差0.5 dB,并随着SNR的增大越来越逼近理想MMSE算法。
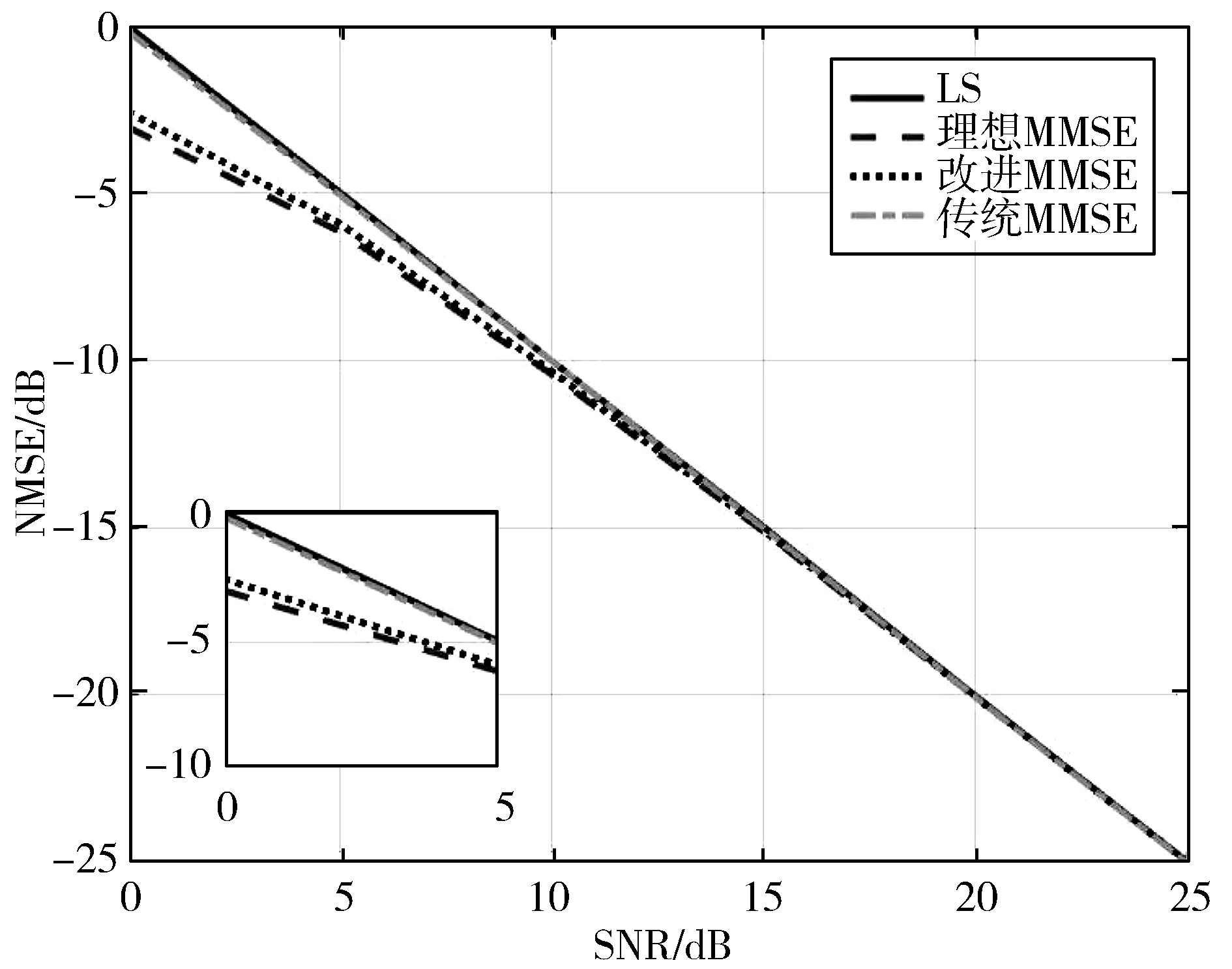
图9 α=0时NMSE曲线对比
从图10中可以看出,在α为0.2即收发天线阵元间存在弱相关性时,改进MMSE算法比传统MMSE算法的准确度有明显的提升。在NMSE为-4 dB时,传统MMSE算法的SNR比理想MMSE算法差3.5 dB,改进MMSE算法的SNR比理想MMSE算法仅差0.5 dB,并随着SNR的增大越来越逼近理想MMSE算法。
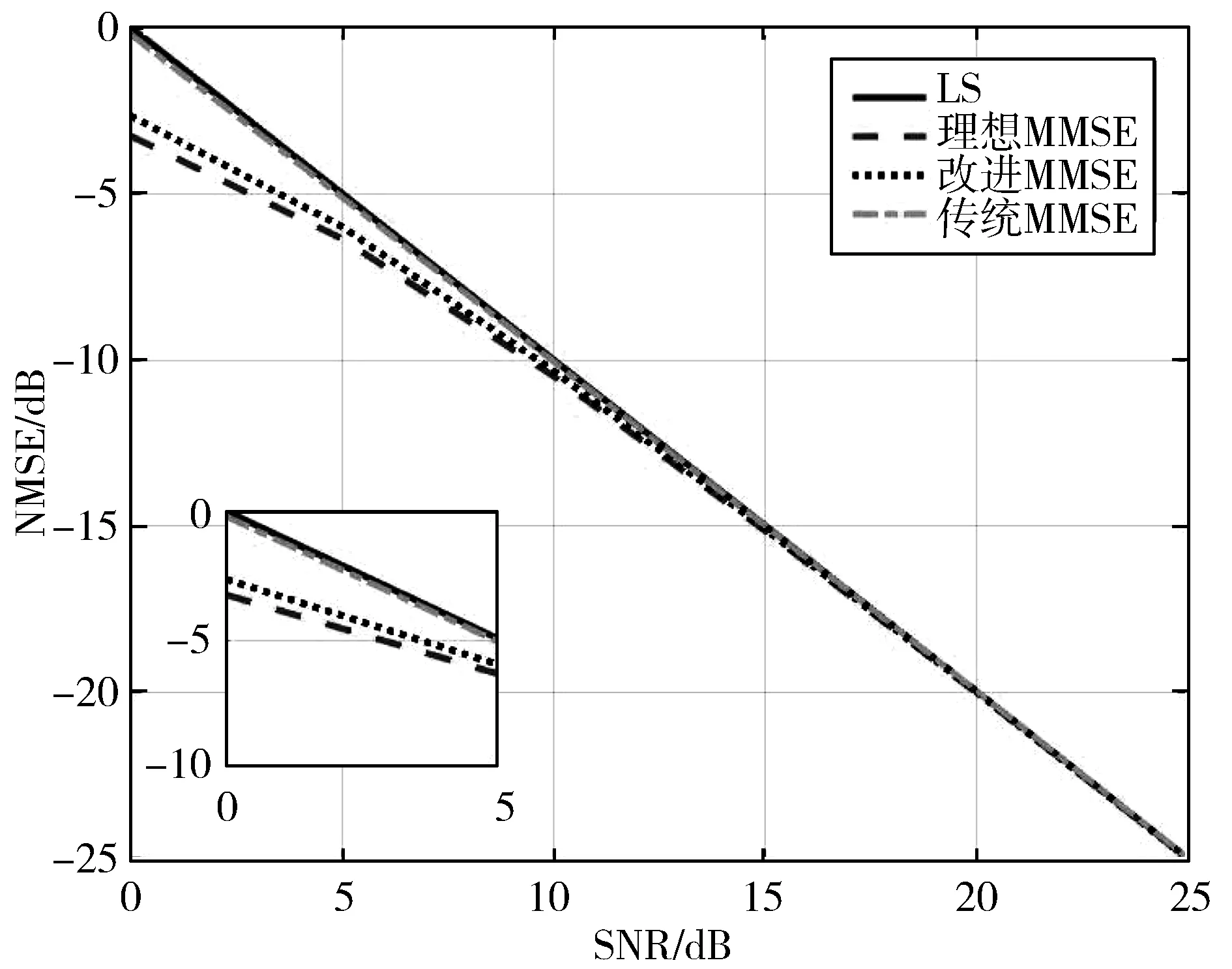
图10 α=0.2时NMSE曲线对比
从图11中可以看出,在α为0.5即收发天线阵元间存在中等程度相关性时,改进MMSE算法比传统MMSE算法的准确度有明显的提升。在NMSE为-6 dB时,传统MMSE算法的SNR比理想MMSE算法差3.5 dB,改进MMSE算法的SNR比理想MMSE方法仅差2 dB,并随着SNR的增大越来越逼近理想MMSE算法。
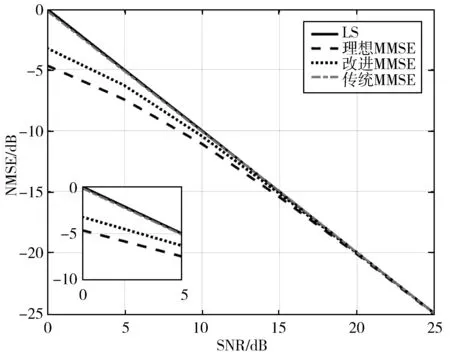
图11 α=0.5时NMSE曲线对比
从图12中可以看出,在α为0.8即收发天线阵元间存在强相关性时,改进MMSE算法比传统MMSE算法的准确度有明显的提升。在NMSE为-8 dB时,传统MMSE算法的SNR比理想MMSE算法差7 dB,改进MMSE算法的SNR比理想MMSE算法差1.5 dB,并随着SNR的增大越来越逼近理想MMSE算法。
图13将加入修正环节前后的改进MMSE算法准确度进行对比,可以看出,在α为0.8即收发天线阵元间存在强相关性时,在NMSE为-8 dB时,未经修正的SNR比加入修正环节后的差2 dB。这意味着:在相同SNR下,未经修正的信道估计准确度更加接近LS算法,经过修正环节后,信道估计准确度有了明显提升。
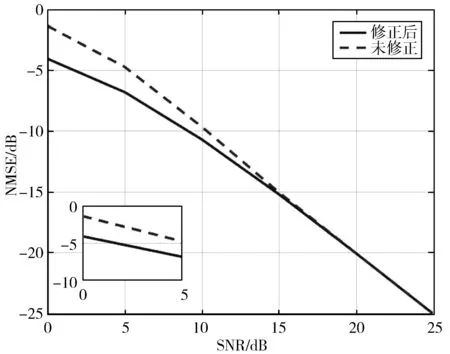
图13 α=0.8时修正前后准确度对比
4 结束语
本文针对配备URA的大规模MIMO散射通信系统的信道估计问题,展开了大规模MIMO散射通信系统信道估计技术的研究。在此系统中,MMSE信道估计算法的精确度高于LS算法。但传统MMSE算法所使用的信道协方差阵是由粗略的统计平均方法获得,使得信道估计效果恶化。本文根据大规模MIMO信道的空间相关性提出了一种信道协方差阵估计算法,通过分析信道协方差阵的元素分布特点,筛选出特定位置的元素对未知参数进行估计,快速恢复出更加准确的信道协方差阵。通过对LS、理想MMSE、传统MMSE和改进MMSE算法的比较,仿真结果表明:理想MMSE算法的准确性最高;LS算法准确性最低;传统MMSE算法的准确性仅比LS算法有微弱提升;改进MMSE算法的准确性优于传统MMSE算法,并随着SNR的增大逼近理想MMSE算法。由此可见,该信道协方差阵估计算法可以使传统的MMSE算法获得改进,从而为此通信系统提供更加准确的CSI。
