钢筋混凝土梁弯曲开裂后有效刚度计算

谷守经，张志华

（天津市政工程设计研究总院有限公司，天津 300392）

钢筋混凝土具有良好的材料整体性、耐火性、耐久性且施工简便，所以许多桥梁都采用钢筋混凝土结构。桥梁在正常使用过程中所发生的损伤主要是由混凝土或钢筋性能退化引起的，其中混凝土的开裂[1]是造成结构损伤的主要原因，研究如何准确评价混凝土结构开裂后的使用性能[2]，具有重要意义。基于黏结滑移理论、无滑移理论、综合理论和数理统计方法，国内外学者对开裂混凝土结构进行了大量的试验研究及理论推导[3～6]，提出多种关于混凝土结构荷载裂缝的计算公式[7～8]，在各自的研究范围内，理论值计算结果均与试验值吻合较好，极大简化了混凝土结构荷载裂缝的计算方法[9～10]。但大部分研究的是平均刚度计算公式，不能准确描述每个梁截面的刚度变化。本文针对钢筋混凝土受弯开裂情况，基于基本假设，建立开裂截面平衡方程，求解截面有效惯性矩，提出精确计算开裂截面有效刚度的计算公式并将理论推导计算值与现行规范计算值进行对比，验证所提出公式准确性。

1 理论推导

1.1 基本假设

1.1.1 本构关系

钢筋应力

式中：fyk为屈服强度标准值；Es为钢筋弹性模量；εs为钢筋应变；εy为钢筋屈服应变；εcu为钢筋极限拉应变。

在混凝土梁截面开裂后，考虑受拉区混凝土的作用，混凝土单轴受拉/受压应力-应变关系采用我国混凝土结构设计规范[11]推荐本构曲线。见图1。

图1 混凝土单轴受拉/受压时应力-应变关系

式中：dc为混凝土单轴受压损伤演化参数；dt为混凝土单轴受拉损伤演化参数；ε为混凝土应变；Ec为钢筋弹性模量。

1.1.2 平截面假设

梁的正截面在受力发生弯曲变形后，仍保持平截面，平行于梁中和轴的各纵向纤维应变与其到中和轴的距离成正比，钢筋与其同一水平线的混凝土应变相等。

1.1.3 应力状态

钢筋和混凝土受压区应力均未达到应力曲线峰值，受拉区边缘混凝土已达到峰值拉应变。

1.2 建立计算方程

当荷载达到开裂弯矩以后，截面受压区合力

式中：xc为受压区高度；b为矩形截面宽度。受压区合力至中性轴的距离

梁截面受拉区合力

式中：h为矩形截面高度；As为受拉区配筋面积。

梁截面受拉区合力至中性轴的距离

式中：h0为矩形截面有效高度。

建立平衡方程

式中：M为截面所受弯矩；ɛc为受压区混凝土边缘压应变；xt为受拉区混凝土屈服应变位置至中性轴的距离；ɛtr为混凝土屈服拉应变；ɛt为受拉区混凝土边缘拉应变。

根据式（8），计算63种不同配筋率、混凝土强度、高宽比的钢筋混凝土梁正截面M/Mcr-Ie/I0；Mcr为截面开裂弯矩；Ie为开裂截面有效抗弯惯性矩；I0为未开裂截面抗弯有效惯性矩。见表1和图2-图4。

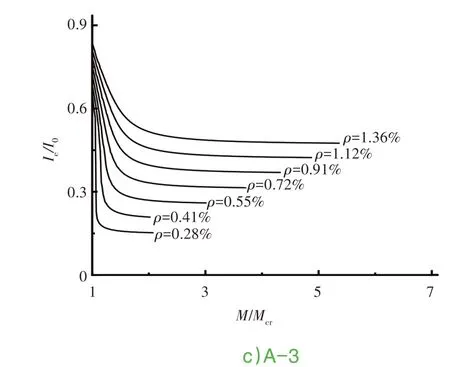
图2 C30混凝土开裂后截面M/Mcr-Ie/I0计算曲线

图4 C50混凝土开裂后截面M/Mcr-Ie/I0计算曲线

表1 截面计算数据

图3 C40混凝土开裂后截面M/Mcr-Ie/I0计算曲线

1.3 限值计算

由以上计算结果可知，混凝土梁在达到开裂弯矩时，截面惯性矩已经发生衰减[12]，在受拉钢筋屈服之后，截面有效惯性矩逐渐趋于稳定，故本文规定当M=Mcr时，截面刚度为开裂后有效惯性矩上限值Imax；当受拉区钢筋屈服时，截面刚度为开裂后有效惯性矩下限值Imin。上限值与混凝土截面高宽比及配筋率有关，与混凝土强度无关；下限值与混凝土强度及配筋率有关，与截面高宽比无关。根据计算结果，建立限值计算基本公式，式中计算参数由拟合确定。

上限值截面有效惯性矩，当M=Mcr时，截面有效惯性矩

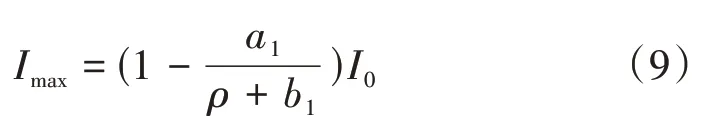
式中：a1与截面高宽比有关,a1=0.56(b/h-0.5)+0.12；b1为计算常数，取b1=0.77。

当Imax/I0＞0.85时，取Imax=0.85。

根据式（9）计算不同截面开裂后的有效惯性矩上限值Imax，见图5。

图5 M=Mcr时Imax/I0与配筋率计算关系

下限值截面有效惯性矩

式中：计算参数a2和b2与混凝土强度有关，见表2。

表2 Imax计算参数取值

根据式（10）计算不同截面开裂后的Imin，见图6。

图6 钢筋屈曲时Imin/I0与配筋率计算关系

1.4 混凝土开裂后M/Mcr-Ie/I0关系计算

钢筋混凝土梁开裂后，截面有效惯性矩在Imax和Imin之间变化，截面有效惯性矩衰减速率与截面配筋率有关，对图2-图4的计算结果进行拟合，建立梁截面M-Ie的曲线公式。

式中：n与截面配筋率有关；Ie为截面有效抗弯惯性矩。

根据式（11）计算面开裂后的M/Mcr-Ie/I0，见图7。

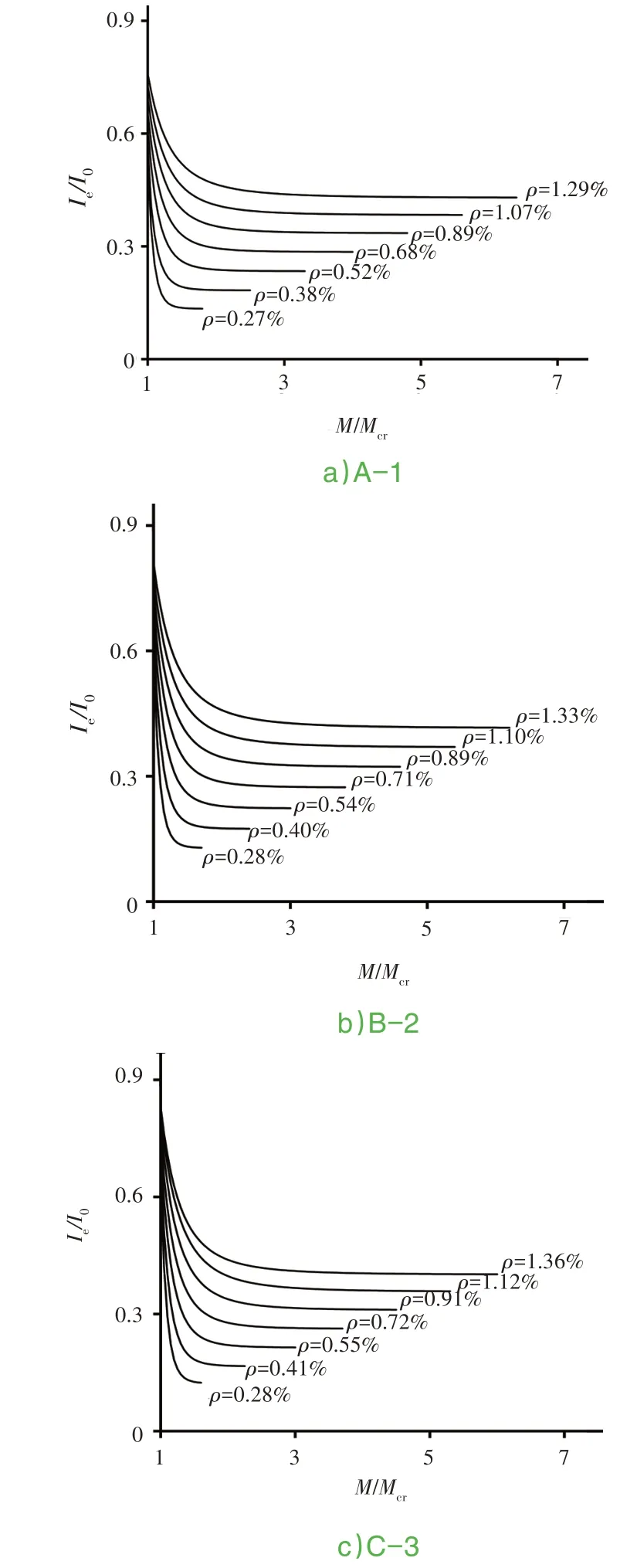
图7 混凝土开裂后截面M/Mcr-Ie/I0计算曲线

2 算例

进行挠度计算时，钢筋混凝土简支梁长L取6 m，进行四点弯曲加载，梁截面取不同高宽比、配筋率、混凝土强度的参数。见图8和表3。

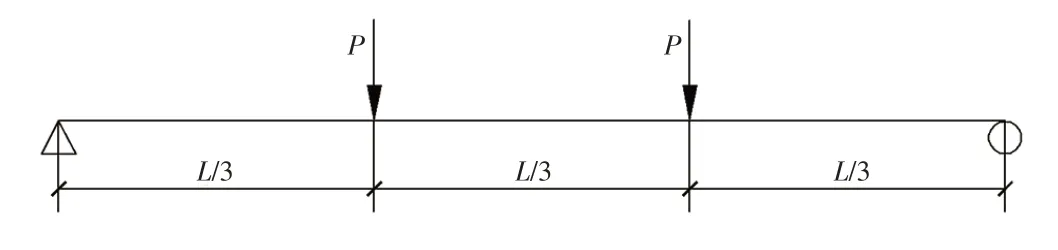
图8 四点弯矩加载计算

表3 截面计算参数

计算时,未达到开裂弯矩的梁截面有效刚度B0取0.85EcI0。

采用本文提出的公式与4种规范[12～15]计算公式及有限元模拟值进行对比，由计算结果可知，在钢筋混凝土梁荷载达到开裂弯矩以后，推导计算挠度值与规范计算挠度值极为接近，说明本文推导公式计算结果与实际相符，可应用到实际工程中。见图9。

图9 弯矩-挠度

3 结论

1）钢筋混凝土梁所受荷载在达到开裂荷载以前，截面抗弯刚度已经发生了退化。荷载达到开裂荷载时，受拉区纵向钢筋配筋率相同时，其有效抗弯刚度刚度上限值（M=Mcr）与截面高宽比有关，截面b/h越大，其刚度比值Imax/I0越大；刚度下限值（受拉区钢筋屈服时）与混凝土强度有关，混凝土强度越高，其刚度比值Imin/I0越小。

2）钢筋混凝土梁在达到开裂荷载以后，其有效抗弯刚度值与配筋率有关，相同截面尺寸条件下，受拉区纵向钢筋配筋率越大，其有效抗弯刚度值越大。

3）钢筋混凝土梁开裂后，随荷载的进一步增大，抗弯刚度在前期下降迅速，而后期下降逐渐平缓直至趋于稳定；截面有效刚度下降速率与受拉区纵向钢筋配筋率有关，配筋率越高，刚度下降速率越慢。

4）利用本文提出钢筋混凝土梁开裂后有效刚度计算公式进行四点弯曲算例分析，结果证明了本文提出计算方法的准确性，所以采用本文计算方法所得数据可作为实际工程计算的参考。