数学建模思想融入数值分析课程教学探析*

刘美春 王芬

（广东金融学院 金融数学与统计学院）

一、引言

数学建模是基于实际问题，抽象简化构建数学模型，求解数学模型得到数学结果，基于结果，解释实际问题，并分析其合理性。数学建模解决实际问题的过程实际就是运用相关理论进行实践的过程[1]。

随着全国数学建模竞赛的发展壮大，数学建模的影响力进一步提升。在2020年，数学建模的实践和活动被列入全国高级中学的教学计划[2]。数学建模思想的重要性进一步为广大教育者认可。李大潜建议“将数学建模的精神融入数学类主干课程”[3]。近年来，相关研究也很多[4-6]。

数值分析是数学专业的专业必修课程，以及部分理工科类专业本科或者研究生的数学基础课程。它研究如何利用计算机求解各类数学问题的近似值问题，教学内容包括插值法、曲线拟合、数值积分、线性方程组求解等，既有数值计算方法的理论学习，如算法稳定性、收敛性、误差分析等等，也研究数值计算方法的计算机实践[7]。因此，数值分析课程既包含数学理论，具有纯数学的抽象性与科学性，而其课程背景和性质，又使得具有强应用性和实践性[8]。

将数学建模思想融入数值分析课程是可行而且有利的。本文将讨论将数学建模思想融入数值分析课堂的相关问题。

二、数学建模思想与数值分析学科的融合点

数值分析学科兼具纯数学理论抽象性和应用的实践性。把数学建模思想应用于数值分析课堂，为数值分析课程理论性和实践性搭建沟通桥梁，是可行的。

首先，数值分析研究是数学建模过程的重要环节。数学建模解决实际的生活、生产过程问题，其过程包括了从实际问题中进行抽象简化以构建数学模型、基于模型寻找或者设计合理的数值计算方法/方案以求解数学建模、基于数值方法上机计算以求出结果、基于结果解释实际问题以得到实际问题的解决方案等多个环节，如图1所示。其中，利用数值计算方法进行模型求解是数值分析课程研究的内容。

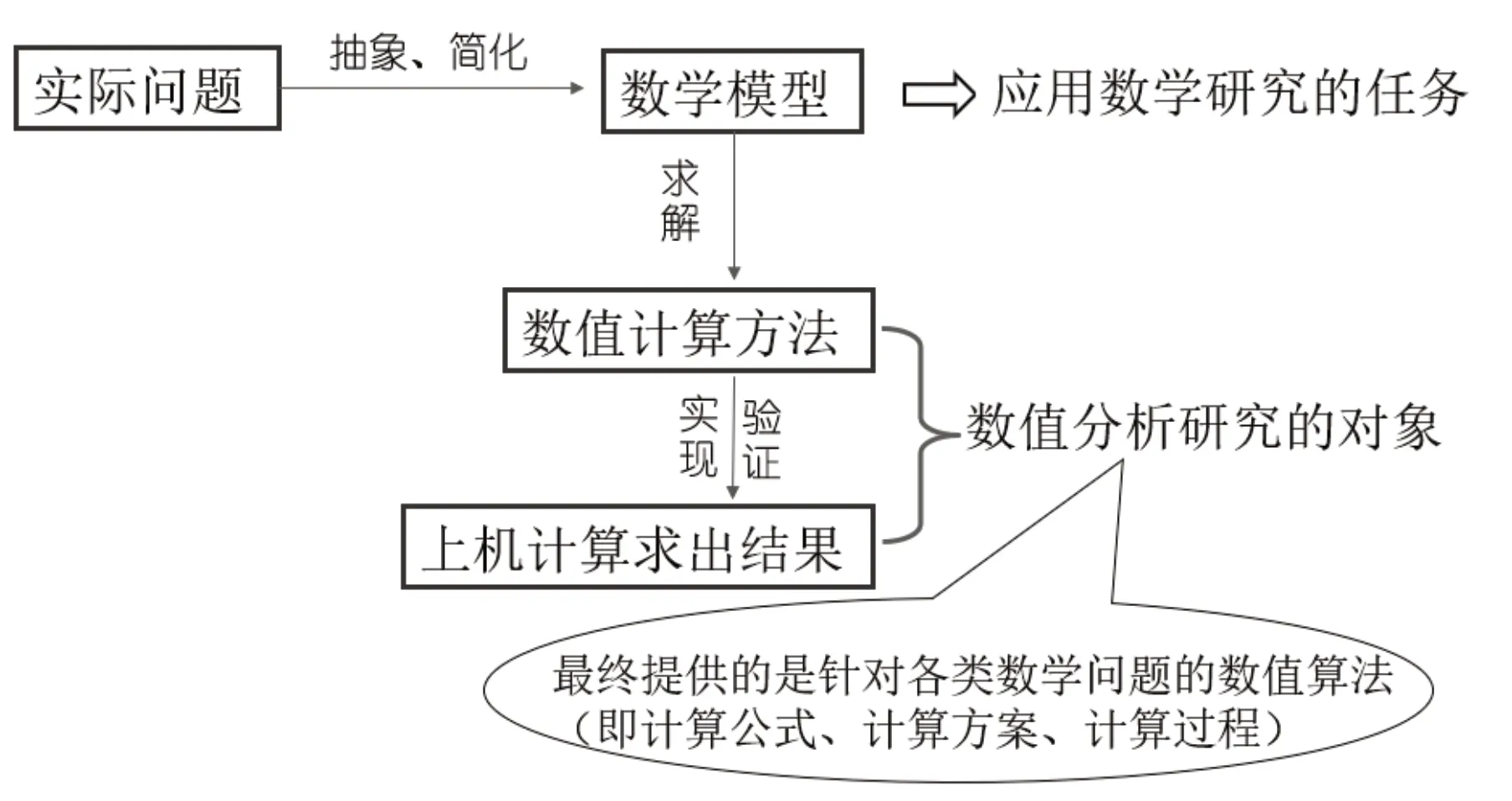
图1 用数学和计算机解决实际问题的过程

其次，“近似”思想是数学建模和数值分析学科共有的思想方法。数学建模在利用数学及相关理论解决实际问题的过程处处有误差。构建模型是基于对实际问题的抽象简化，会产生模型误差；测量或者观测确定数学模型的参数时，会产生观测误差；利用数值算法求解模型会由于方法本身产生截断误差，上机计算会由于计算机字长限制等产生舍入误差。所以，“近似”是贯穿数学建模整个过程的思想方法。而数值分析讨论的是各式数学问题的近似值，“近似”是数值分析学科核心的思想和方法，误差分析是数值分析的各种算法的理论分析中不可或缺的环节。数学建模思想的融入将加深学生对数值算法“近似思想”的理解和体验。

最后，部分数值分析的理论是基于数学建模解决实际问题的需求而产生。

恩格斯说：“数学是从人们的实际需要中产生的。”荷兰数学教育家弗赖登塔尔说：“数学来源于现实，扎根于现实”。同其他数学课程一样，数值分析的大多算法来源于实际问题的需要，基本都被应用于解决实际的问题，其各种算法的形成、算法应用过程便是完整的数学建模的过程。例如，在实际应用中需要利用解析函数进行数据描绘的需求。而已知条件是函数表格，各种情况（自变量）下，监控目标出现的相应特征（因变量）已知，但自变量与因变量之间的关系未知；又或者自变量与因变量的映射关系已知，但不便于计算，需要找潜在函数的近似函数。于是，便出现了插值法和曲线拟合法，二者基于不同的近似假设构建近似函数，满足不同的实际需求。再比如，许多实际问题可以归结为定积分的求解。按牛顿-莱布尼兹公式，定积分的值等于被积函数的原函数在积分上下限的函数值的差。而在实际问题中，有时会遇上困难。比如有些被积函数原函数虽然存在却无法用初等函数表示，或者原函数表达式非常复杂，或者被积函数是用图表表示，就无法使用牛顿-莱布尼兹公式直接求解，需要求定积分的近似值。因此产生了数值积分。这些数值理论的产生背景为构建实际问题案例提供了参考。

因此，把数学建模思想融入数值分析课堂教学是可行的。

三、数学建模思想融入数值分析课程教学的意义和方法

数值分析研究各种不同的数学问题近似解求解问题，这些数学问题大多来源于先修的课程，如高等数学、线性代数、常微分方程、数学建模、计算机编程等，因此，数值分析教学内容涉及面广；数值分析每一章针对不同的数学问题，各章节内容之间相对独立，章节连贯性较差；数值分析既有繁琐的公式，有复杂的理论分析，如收敛性、稳定性分析、误差分析等等，也要求算法实践。数值分析问题来源于各类生活生产、工程、经济中的实际问题，要授予学生各类算法的数学知识、原理，锻炼学生逻辑思维能力，更要培养学生学以致用，学会分析问题、解决实际问题的能力。教学实践证明，数值分析的教与学都极具难度[8]。

与多数课程一样，数值分析传统课堂的教学方式为“老师在讲台上讲授，学生在下面座位上听讲”的“灌输式”。课堂上更偏重理论知识的讲授，注重算法的思想、定理的推理证明、公式的推导等，并通过例题、练习来巩固相关理论，课程实验的上机实践主要是算法的实现。传统教学模式强调理论知识结构的完整、逻辑思维的严密性，能帮助学生有效完成知识积累。然而，传统教学模式内容比较枯燥，特别是数学理论比较抽象、晦涩难懂，教授方式也比较单一，都会影响学生学习的积极性；另一方面，传统教学方式对知识的应用性重视不够，对学生学以致用、分析问题、基于理论解决实际问题能力的培养和训练不够。事实上，这些能力是学生在当今这个信息爆炸时代生存和发展的重要保证，具备这些能力，他们才能更好地利用海量的碎片化的信息。而这也正是高等教育目标。

将数学建模思想融入数值分析课程的教学，利用数学建模“沟通数学与应用的桥梁”的功能，有利于改善传统教学的“重知识轻实践”的不足。

（一）重视教学案例的应用，在教学中融入数学建模思想

理论与实践并重是数值分析课程的特点，“用数学”也是数学教学的主要目的之一。数学建模是应用数学及相关理论解决实际问题的过程。因此，案例教学是数学建模思想融入数值分析课堂教学的重要手段。

比如，利用案例进行概念教学，可以使抽象的概念形象化。第一章中的概念 “舍入误差”是浮点数在计算机上表示或者计算时，由于字长的限制进行舍入引起的误差。可使用“因特尔奔腾处理器缺陷”案例加深学生对舍入误差的认识。数学家托马斯∙莱斯利教授拟计算素数的倒数之和，其使用的模型合理（旧计算机计算结果正确），但在装有新奔腾芯片的计算机上运算结果却跟理论计算结果不符。这件事发酵到最后，结果是确认因特尔公司新芯片有缺陷，导致“舍入误差”设计方面不合理，公司不得不预留出4.2亿美元的补偿金。该案例不仅让学生对舍入误差有深刻认识，一个小误差最终导致天价的赔偿，也让学生对误差分析的重要性有了更深的体会。

再如，案例教学还可以把数值分析课程不同章节的内容连接起来，甚至把数值分析与其他先修课程的内容联系起来，达到了融会贯通、学以致用、“用数学”的目的。函数逼近（插值法/曲线拟合）和数值积分分属不同的独立章节。用 案例“某地居民用水量”把课程“插值法”“曲线拟合”的内容与“数值积分”内容连接起来。如表1所示。

表1 某地居民用水量案例[9]

案例教学中，通过有实际生产或生活背景的应用示例，有利于激发学生们学习兴趣和热情，更好地掌握相关算法思想、算法应用等，也进一步提高其应用数学的能力。

按照数值分析学科特点，可以多渠道挖掘、选择合理的案例。

（1）依照概念、定理、算法的数学背景，或者应用场景选择案例。例如前面提到的“舍入误差”，源于计算机对数据字长的限制，因此可以从相关领域选择案例。另外，数值分析的许多算法源于各类生活生产、工程、经济中的实际问题。比如，样条插值的产生是由于某些实际生产问题要求插值函数不仅连续，而且要有较好的光滑性，比如飞机的机翼外形、内燃机的进、排气门的凸轮曲线等，不仅要求近似曲线是连续的，对曲线的光滑度也有要求，曲率要连续（一阶、二阶导连续），后者普通的插值算法无法保证，因此出现三次样条插值技术。因此，可以在“三次样条插值”的教学中选择“绘制直升飞机旋转机翼外形轮廓线”的案例。再比如前面提到的“居民用水”案例则源于算法应用。

（2）利用数值分析与先修课程的关系，拓展案例来源。数值分析研究的是各类数学问题的近似解求解方法，而其中一些问题来源于其他先修课程。比如数值积分、线性方程组求解，分别来源于高等数学/数学分析、高等代数/线性代数等课程。可以寻根溯源，根据数学问题的来源来选择合适的示例。例如前面所提到的“居民用水量”案例，追溯其根源，归属为定积分的应用问题（数学分析课程）。另外，线性方程组问题归属于高等代数，微分方程问题归属于常微分方程等等。

（3）从数学建模竞赛题目中选择合适的题目作为案例。模型求解是数学建模的重要环节，在模型求解中往往需要用到数值分析方法。在数学建模题目中，常有涉及数据处理与统计分析方面的题目，可以选择作为案例。

（二）利用线上平台辅助教学，线上线下融合，多渠道融入数学建模思想

各类数学问题的数值方法及其上机实现，算法思想、算法分析及算法实现是数值分析课程的主要研究对象，课程教学的重点。“基于教学案例融入数学建模思想”是辅助的教学手段，使学生了解算法的来龙去脉，了解算法的应用，巩固对算法的理解。课堂教学应该主次分明，不可喧宾夺主。

而事实上，从案例的引入到数值算法的使用到实际的应用，中间涉及复杂的计算分析。比如案例为实际生产问题的建模求解时，其完整过程包括抽象简化、建模、求解、分析检验等，数值分析方法的选择与使用只是模型求解中的一个环节。课堂上，为了更有效利用时间，主次分明，除了数值计算的使用，其他相关步骤都被不同程度地简化。学生的基础不同，接受程度也不同，为了给学生呈现完整建模求解过程，可以采用线下为主，线上为辅的线上线下融合的教学方式。借助线上教学平台，以教学辅助资料、教学小视频等方式完善实际问题的数学建模，或者提供建模思路，供学生学习参考，这也是数学建模思想的融入方式。

除了课堂，线上辅助教学平台，还可以利用课后作业、课程实验等渠道融入数学建模思想。例如，课后作业除了传统的计算题，可以增加具有实用背景的应用性题目；课程实验，除了算法的实现内容，还可以增加类似于数学建模内容的实际生产生活问题，允许双人合作或者多人的团队合作，并以课程论文替代常规的实验报告等等。

四、结语

数值分析是大学数学类专业的专业必修课程，有纯数学课程的严谨抽象，也具有很高的实践性要求。数学建模具有“沟通数学与应用的桥梁的功能”，把数学建模思想融入数值分析课程的教学，符合数值分析课程的特点。数学建模思想的融入，有利于抽象理论与其实践应用的有机融合，激发学生对算法应用、算法实现的兴趣，巩固学生对算法的理解与掌握，同时培养学生理论运用于实践的能力，值得继续探索。