基于差值法的实心铆钉紧固压力和压强测量方法
2022-12-29苏佳文
刘 泽,刘 松,苏佳文
(中国直升机设计研究所,江西 景德镇 333001)
0 引言
铆接具有连接构件强度稳定可靠、工艺过程简单、质量检查和排故比较容易及对裂纹损伤有一定的止裂作用等优点,在飞机装配中得到了广泛应用[1]。与抽芯铆钉相比,实心铆钉在铆接成型过程中,钉杆在铆枪的冲击力作用下膨胀变形,将钉孔完全填充形成紧密配合;钉杆端部在挡铁阻挡下镦粗变形形成镦头,可有效紧固被连接构件,具有更高的铆接强度[2];且其制造成本更加低廉,在飞机铆接装配中使用量巨大。目前铆接方面大部分的研究集中在铆钉抗剪力学性能分析、铆接过程中铆钉的变形、受载规律和铆钉排布优化设计[3-9],少部分对铆接后的残余应力进行了分析。但由于很难进行试验测量,上述研究主要为有限元仿真分析[10],目前尚无测量铆钉的紧固压力和压强的试验方法。实心铆钉的紧固压力和压强影响连接结构的铆接强度,因此,设计试验测量方法,了解实心铆钉的紧固压力和压强的情况,对研究实心铆钉的铆接强度校核方法具有重要的工程参考价值。
基于上述原因,本文提出了一种实心铆钉的紧固压力和压强测量方法,该方法基于差值法间接测量;设计了测量试验,给出了试验件的结构和设计要求,详细说明了试验设备、试验原理及试验测量内容;基于试验测量的摩擦力矩,利用差值法推导了普通型实心铆钉和沉头实心铆钉的的轴向紧固压力和径向压强的计算公式。
1 实心铆钉的紧固压力和压强测量试验
1.1 试验件
图1为试验件1结构示意图,为带凸台结构零件,其中凸台带有铆钉孔。图2为试验件2结构示意图,为长条形板,其中一端为半圆形且带有铆钉孔,试验时与试验件1凸台部分铆接,如图3所示。试验件2宽度D0要略大于试验件1凸台直径D。本试验通过测量试验件1凸台部分与试验件2之间的摩擦力矩间接换算出实心铆钉的紧固压力和压强,需要假设两试验件接触面内的压强各点相等。因此,在空间能够满足铆接的情况下,凸台直径D应尽量小。试验件1的凸台和试验件2板应具备一定厚度(分别为h,h0),以保证拥有足够的刚度,避免试验时产生过大变形。对于常用的Φ4 mm铆钉,试验件厚度达到3 mm即能满足刚度需求。本文将铆钉的钉头设计在试验件1一侧。

图1 试验件1结构示意图
通过差值法推导求解实心铆钉的紧固压力和压强,因此规定试验件1与试验件2的材料相同,且具有2种表面状态(改变试验件的表面粗糙度或镀层等条件),并规定在不同组合下,试验件1与试验件2相互之间的摩擦系数分别为μ、μ′和μ″,具体见表1。

图2 试验件2结构示意图

图3 试验件1与试验件2铆接示意图

表1 摩擦系数
1.2 测量试验
图4所示为实心铆钉的摩擦力矩测量试验示意图。在试验台架上安装可调功率电机,将试验件1和试验件2铆接并按图示固定安装在电机和台架上,试验件2与台架连接端部接有力传感器,L为连接端部距铆钉中心距离。试验时,缓慢增加电机输出功率,使试验件1由静止向匀速转动,测得最大力值F0。因此,试验件1和试验件2之间摩擦力产生的总力矩为:
M=LF0
(1)

图4 摩擦力矩测量试验示意图
测量试验件1和试验件2不同表面状态组合下的摩擦力矩M(1)、M(2)、M(3),具体见表2。

表2 摩擦力矩测量
2 轴向紧固压力和径向压强计算公式
图5为实心铆钉铆接示意图。设轴向紧固压力为N,径向压强为P,钉孔的圆柱面积为S0,则径向压强产生的挤压力:
N′=PS0
(2)
钉孔为光滑的金属内壁,其与钉杆的摩擦系数可由相应等效试验测量,此处设其为v。

图5 实心铆钉铆接示意图
2.1 普通型实心铆钉
如图6所示,设铆钉的直径为d,钉头直径为d1,镦头直径为d2。设试验件1和试验件2之间的摩擦力的力矩为M1,如图7所示,采用积分计算。
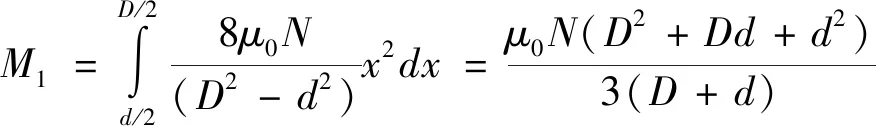
(3)
式中,μ0根据两试验件接触面情况取值(μ、μ′或μ″)。
径向挤压力N′如图8所示,摩擦力沿切线方向,因此N″产生摩擦力的力矩:

(4)
设钉头和镦头与试验件之间的摩擦力的力矩为M3,钉头和镦头与试验件摩擦区域的外径分别为d1和d2,由M1推导可知:

(5)
式中,μ1为钉头与试验件1之间的摩擦系数,μ2为镦头与试验件2之间的摩擦系数,可由等效试验测量;为便于公式推导的整齐化,对于3组摩擦力矩测量试验,对应的摩擦系数μ1、μ2采用表3的表示方式。

表3 摩擦系数μ1和μ2
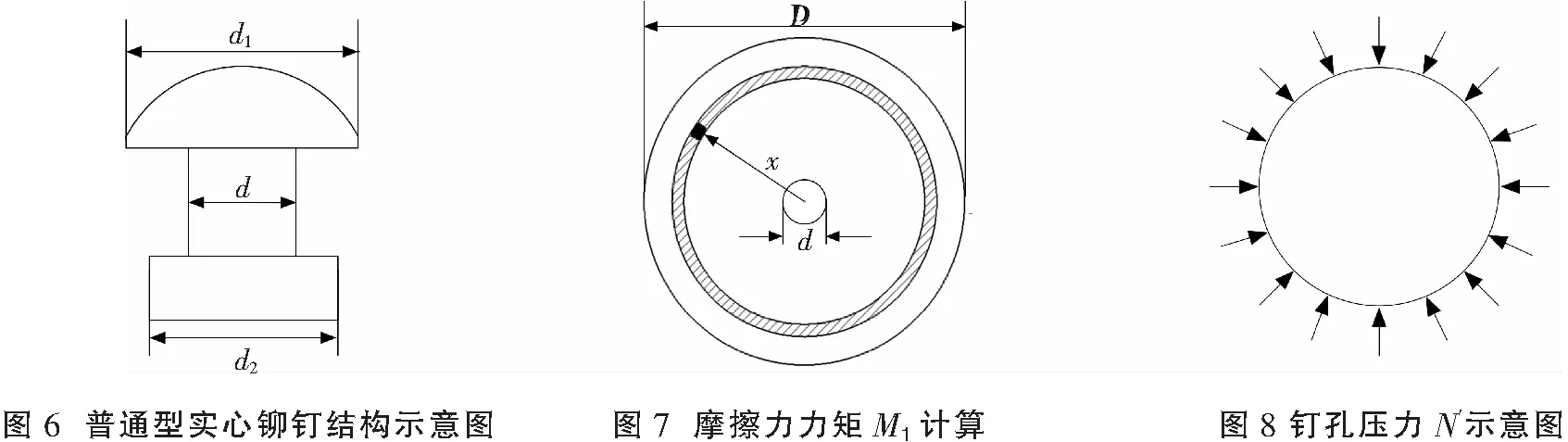
为简化公式形式,令:
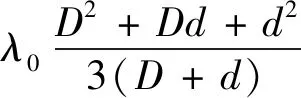
(6)

(7)
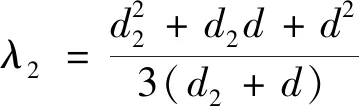
(8)
由力矩平衡有:
M=M1+M2+M3
(9)
对同种铆钉,当铆钉直径d相同时,摩擦力矩M2相同,因此,当按表2进行试验时,有:
M(1)=N[λ0μ+λ1μ1(1)+λ2μ2(1)]+M2
(10)
M(2)=N[λ0μ′+λ1μ1(2)+λ2μ2(2)]+M2
(11)
M(3)=N[λ0μ″+λ1μ1(3)+λ2μ2(3)]+M2
(12)
式(11)-式(10),式(12)-式(10),式(12)-式(11),则有:
N(1)=
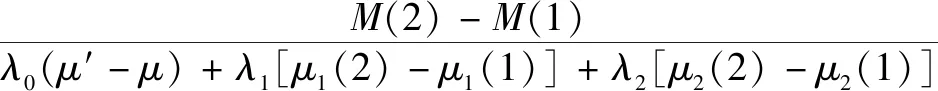
(13)
N(2)=

(14)
N(3)=
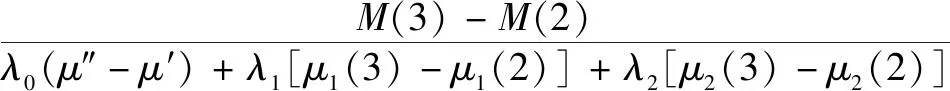
(15)
式中,N(1)、N(2)、N(3)为3次差值求得的轴向紧固压力,对其求平均:
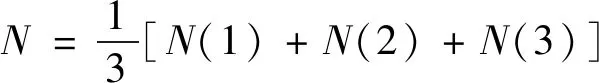
(16)
将轴向紧固压力N带入式(10)、式(11)、式(12),求得径向挤压力:
N′(1)=
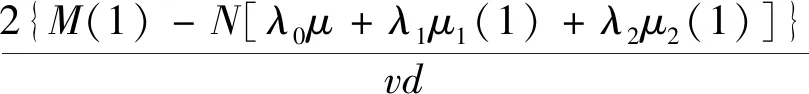
(17)
N′(2)=
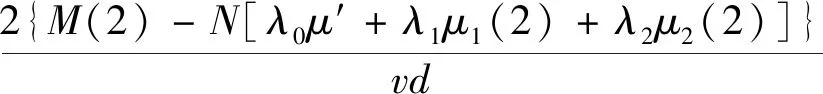
(18)
N′(3)=

(19)
对其求平均:
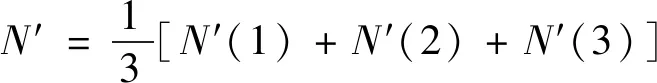
(20)
将N′带入(2)式求得径向压强P。
2.2 沉头实心铆钉
如图9所示,沉头铆钉的沉头度数为θ,沉头深度为w,镦头的直径为d3,试验件上的沉头锪窝也为光滑的金属内壁,因此,铆钉沉头与锪窝之间的摩擦系数为v;同样设试验件1和试验件2之间的摩擦力的力矩为M1,径向挤压力N′产生的摩擦力的力矩为M2,设沉头钉头和镦头与试验件之间的摩擦力矩为M3;由(3)式和(4)式可知,沉头铆钉的摩擦力矩M1和M2与普通型铆钉的计算公式相同,因此,仅需推导M3的计算公式。
对于沉头铆钉,沉头所受的铆接压力需进行分解,如图10所示,沉头的垂直压力为:
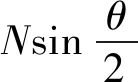
(21)

沉头侧面积:
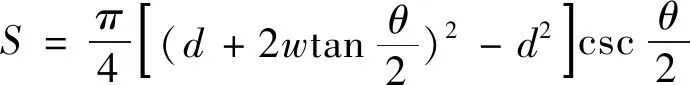
(22)
镦头与试验件2之间的摩擦力的力矩与普通型铆钉的计算相同,如图11所示。沉头部分则通过积分计算:
M3=

(23)
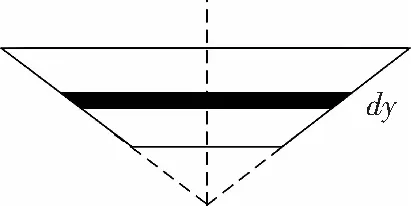
图11 沉头摩擦力力矩计算
为简化公式形式,令:

(24)
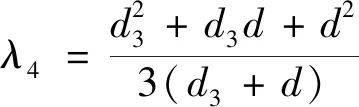
(25)
满足式(9)平衡方程,且对同种铆钉,当铆钉直径d相同时,摩擦力力矩M2相同,因此,当按表2进行试验时,有:
M(1)=N[λ0μ+λ3+λ4μ2(1)]+M2
(26)
M(2)=N[λ0μ′+λ3+λ4μ2(2)]+M2
(27)
M(3)=N[λ0μ″+λ3+λ4μ2(3)]+M2
(28)
式(27)-式(26),式(28)-式(26),式(28)-式(27),则有:
按(16)式对N求平均后带入式(26)、式(27)、式(28),求得径向挤压力:
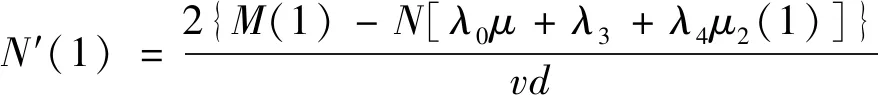
(32)

(33)
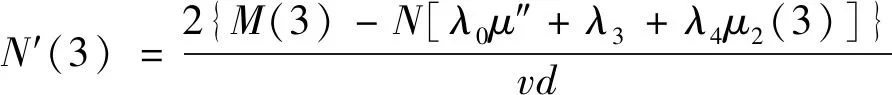
(34)
按(20)式计算N′平均值,带入(2)式求得径向压强P。
3 试验件厚度和摩擦系数设计要求
上述试验测量方法是基于所有摩擦力矩均达到最大值,因此有:
M2(试验件1)+M3(试验件1)=
M2(试验件2)+M3(试验件2)
(35)
式中,M2(试验件1)、M2(试验件2)分别为试验件1、试验件2与钉杆的摩擦力矩,M3(试验件1)为试验件1与钉头的摩擦力矩,M3(试验件2)为试验件2与镦头的摩擦力矩。
对于普通型实心铆钉,式(35)为:
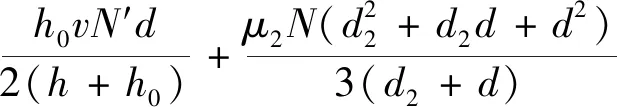
(36)
存在N和N′两个未知量,当h=h0时可消除两未知量,则有:
式(37)即普通型实心铆钉摩擦系数的理想条件,在试验设计中尽量保证等式左右数值相近,以减小试验测量误差。
对于沉头实心铆钉,式(35)为:

(38)
当时h=h0,则有:
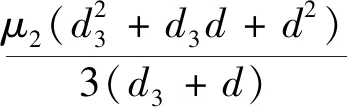
(39)
因此,试验件1和试验件2厚度相等。为减小试验测量误差,普通型实心铆钉和沉头实心铆钉应尽量保证(37)式、(39)式等号两侧的数值相近。
4 结论
针对目前实心铆钉的紧固压力和压强尚无试验测量方法这一问题,本文提出了一种基于差值法的间接测量方法,具体如下:
1)设计了实心铆钉铆接的摩擦力矩测量试验,给出了试验件的结构和设计要求,详细说明了试验设备、试验原理及试验测量内容;
2)基于试验测量的摩擦力矩,利用差值法间接计算实心铆钉的紧固压力和压强,由摩擦力力矩平衡,推导了普通型实心铆钉和沉头实心铆钉的轴向紧固压力和径向压强的计算公式;
3)采用旋转法测量总摩擦力矩,在试验过程中,铆钉仅受到轴向紧固压力、径向挤压力和摩擦力作用,保证了试验测量的有效性和准确性;
4)计算公式中考虑了试验件1和试验件2、钉头和试验件1、镦头和试验件2、钉杆和钉孔的摩擦力力矩,与实际铆接情况相同,保证了计算公式的有效性和准确性。
