基于多分支网络的深度图帧内编码单元快速划分算法

刘 畅 贾克斌 刘鹏宇

(北京工业大学信息学部 北京 100124)

(先进信息网络北京实验室 北京 100124)

(计算智能与智能系统北京市重点实验室 北京 100124)

1 引言

随着多媒体信息技术的飞速发展，视频电视也在不断更新。一方面，视频电视由标清向高清甚至全高清发展，可支持的像素个数越来越多；另一方面，视频电视由平面2维向3维甚至自由视点发展，可支持的视点个数越来越多。从标清到全高清、从平面到立体，视频技术历经数次革新，已阔步迈向超高清时代。伴随新一代信息通信技术的升级，独具大带宽、广连接、低时延的第5代移动通信技术(5th Generation mobile communication technology, 5G)[1]无疑为视频应用搭建起“高速车道”。

在这一背景下，传统的2维(Two Dimensional,2D)[2]视频已难以满足新时代人民群众对美好视听的新需求，具备大视角、高画质以及画面包围感的沉浸式视频应用而生，其主要包括立体视频、多视点视频[3]、360°平面视频、虚拟现实 (Virtual Reality, VR)以及增强现实(Augmented Reality, AR)等。其中，作为多媒体信息产业的热点之一，多视点视频依托视频技术的全面突破，集“交互性”和“临场感”特质于一身，颠覆了传统视觉体验，成为学术界和工业界关注的新焦点。然而，多视点视频的出现是一把双刃剑，它在为人们带来更具感染力和沉浸感的视觉盛宴的同时，也使得数据量呈指数级增长，带宽开销激增。一直以来，寻求带宽成本与高品质视觉体验的平衡是视频编码技术的永恒主题。为降低因视点个数增多带来的数据量的增加，需采用更有效的视频编码方案。

面对视频编码技术的新要求，3维高效视频编码(Three Dimensional-High Efficiency Video Coding, 3D-HEVC)[4]标准应运而生。它的发展历程主要有两个关键时间点。第一，2012年7月，运动图片专家组(Motion Picture Expert Group, MPEG)和视频编码专家组(Video Coding Expert Group,VCEG)合作组成3维视频联合编码组(Joint Collaborative Team on Three dimensional Video,JCT-3V)，共同开发下一代3维视频编码标准。第二，2015年2月，3D-HEVC国际标准正式发布。截至目前，3D-HEVC是最新的3维(Three Dimensional, 3D)视频编码标准。3D-HEVC采用的视频编码格式是多视点纹理加深度(Multiview Video plus Depth, MVD)[5]。MVD由2～3个视点的纹理图及其对应的深度图组成，其采用基于深度图像的绘制(Depth Image-Based Rendering, DIBR)[6]技术实现任意虚拟视点的合成，通过减少视点数量来降低待编码视频的数据量。MVD视频格式的出现缓解了因视点数增加导致数据量激增的问题，是目前最为有效的3D视频编码格式。

与高效视频编码(High Efficiency Video Coding, HEVC)[7]标准相比，3D-HEVC引入了深度图。与纹理图不同，深度图表示物体与相机的距离。为区别于纹理图的特征，3D-HEVC提供了众多复杂的深度图编码技术，导致3D-HEVC编码复杂度提升，深度图编码复杂度可达纹理图的3～4倍。其中，深度图编码单元(Coding Unit,CU)划分的复杂度占深度图编码复杂度的90%以上，这成为阻碍3D-HEVC在实际应用领域推广使用的一个关键问题。因此，面对新形势、新挑战，为解决上述问题，众多国内外学者从加快深度图编码方面展开研究。

目前，针对深度图的快速编码可分为3类，分别为基于启发式的方法[8–10]、基于机器学习的方法[11–13]以及基于深度学习的方法[14–16]。其中，基于启发式的方法大多是基于阈值、率失真代价(Rate Distortion cost, RD-cost)或时间/空间/视点间相关性提出的。但该类方法依赖人为制定决策规则，对于各具特点的视频序列，单一或不全面的特征提取方法导致算法鲁棒性差。进一步，有学者利用机器学习方法来加速深度图编码，早期研究方法主要是基于决策树，通过构建静态决策树，利用数据挖掘提取视频特征。但该类方法依赖手工提取特征，获取的是底层简单的物理特征，特征表征能力较差。近年来，随着深度学习技术的进步和普及，一些学者将其应用到不同的视频编码领域中，包括前一代视频编码标准H E V C，新一代视频编码标准VVC(Versatile Video Coding)以及HEVC的扩展标准3D-HEVC。针对3D-HEVC而言，文献[17]利用整体嵌套的边缘检测(Holistically nested Edge Detection, HED)网络检测深度图的边缘，通过基于深度学习网络的边缘检测对3D-HEVC深度图进行帧内快速预测编码，然而文献[17]采用的HED网络是基于复杂网络结构的视觉几何群网络(Visual Geometry Group network, VGG-16)[18]，算法性能对硬件依赖性较强，并且这种利用网络实现预测编码方法的本质是对四叉树进行剪枝操作，仍需进行传统的率失真优化(Rate Distortion Optimization,RDO)计算。

针对上述方法存在的不足，本文基于网络的深度特征表达与学习，提出一种基于深度学习的CU划分结构快速预测方案，通过直接预测深度图帧内编码模式下CU的划分结构来降低CU划分的复杂度，进而降低3D-HEVC的编码复杂度，对比实验结果证明了本文算法的有效性。

2 3D-HEVC编码结构及CU划分结构

2.1 3D-HEVC编码结构

一个完整的3D-HEVC测试序列包含3个视点，鉴于3个视点取自同一时刻、不同位置，故不同位置的视点因视角差异而具有轻微的内容差异性。图1以Kendo测试序列[19]为例，展示了3D-HEVC的编码结构。图1的3个视点分别为视点0、视点1和视点2。其中视点0为独立视点，其余两个视点为非独立视点。与HEVC不同，3D-HEVC的编码结构包含纹理图及其对应的深度图。如图1所示，每个视点都包含纹理图及其对应的深度图。

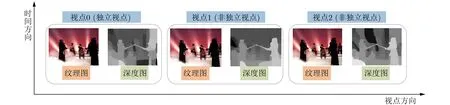
图1 3D-HEVC编码结构

区别于纹理图，深度图具有大面积的平滑区域和显著的边缘。为准确地编码深度图的边缘，3DHEVC引入了深度图编码技术，但新技术的引入也带来编码复杂度的增加。图2展示了6个标准测试序列的编码时间统计结果。如图2所示，深度图的编码时间占总编码时间的80%以上。因此，有必要降低3D-HEVC中深度图的编码时间。

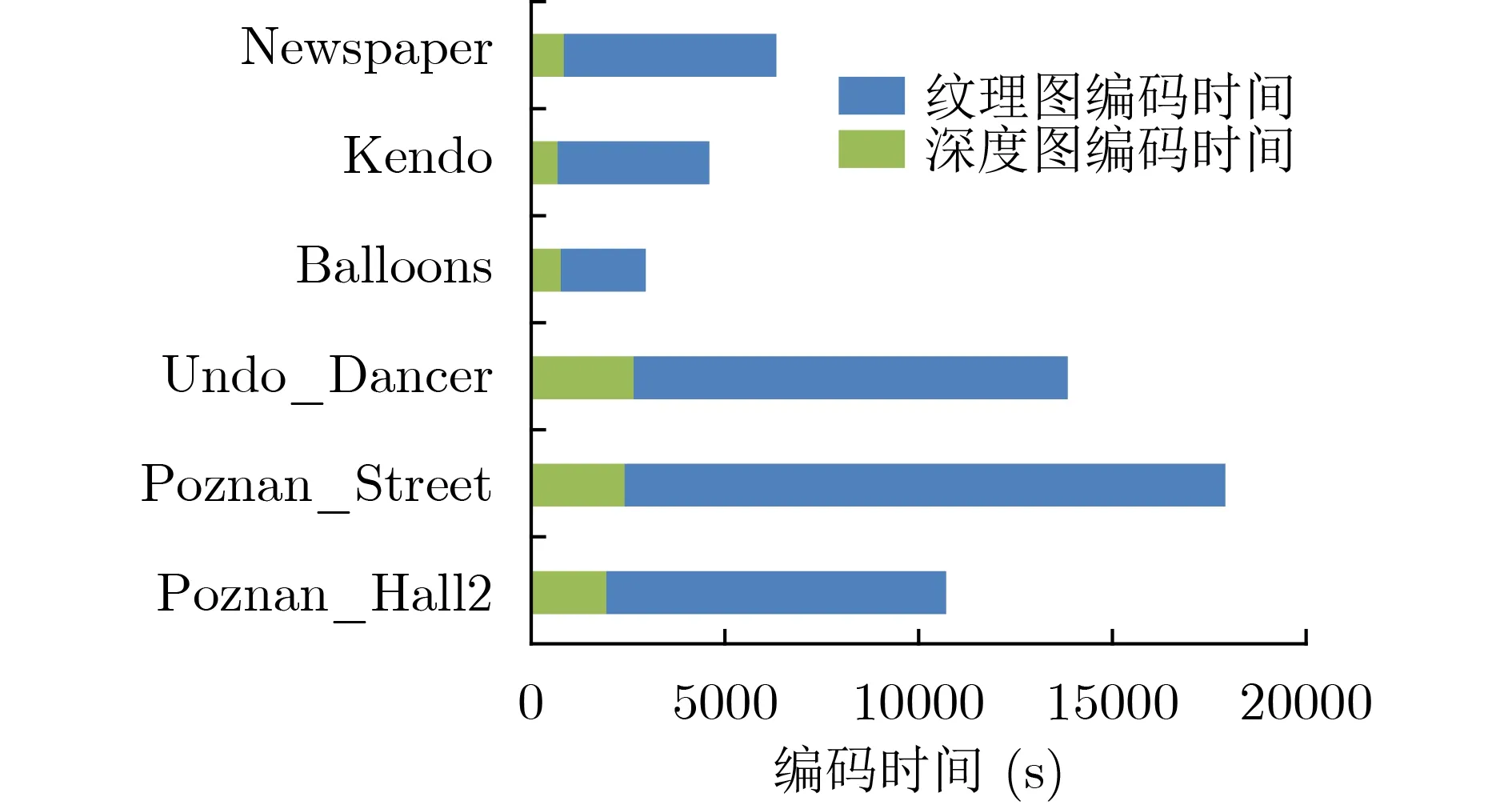
图2 6个标准测试序列的编码时间统计

2.2 CU划分结构

在3D-HEVC深度图中，每帧图像会被分割成若干个非重叠的编码树单元(Coding Tree Unit, CTU)，每个CTU既可以包含单个CU，也可以依据四叉树结构迭代划分为几个较小尺寸的CU。CU的尺寸可以为64×64, 32×32, 16×16, 8×8，对应的CTU深度分别为0, 1, 2, 3。图3展示了深度图中的CTU及其对应的四叉树划分结构。值得注意的是，通过迭代计算才能获得CTU的最佳划分结构。而CTU的四叉树划分不仅包括自上而下的RD-cost计算过程，还包括自下而上的RD-cost比较过程。针对自上而下的计算过程而言，如图3所示，按照“深度=0、深度=1、深度=2、深度=3”的顺序依次计算当前深度下所有编码单元的RD-cost。基于此，再进行自下而上的比较过程。若“RD-cost(深度=n)> RD-cost(深度=n+1), n=0, 1, 2”，则“深度=n”的编码单元需要划分，反之，则不需要划分。

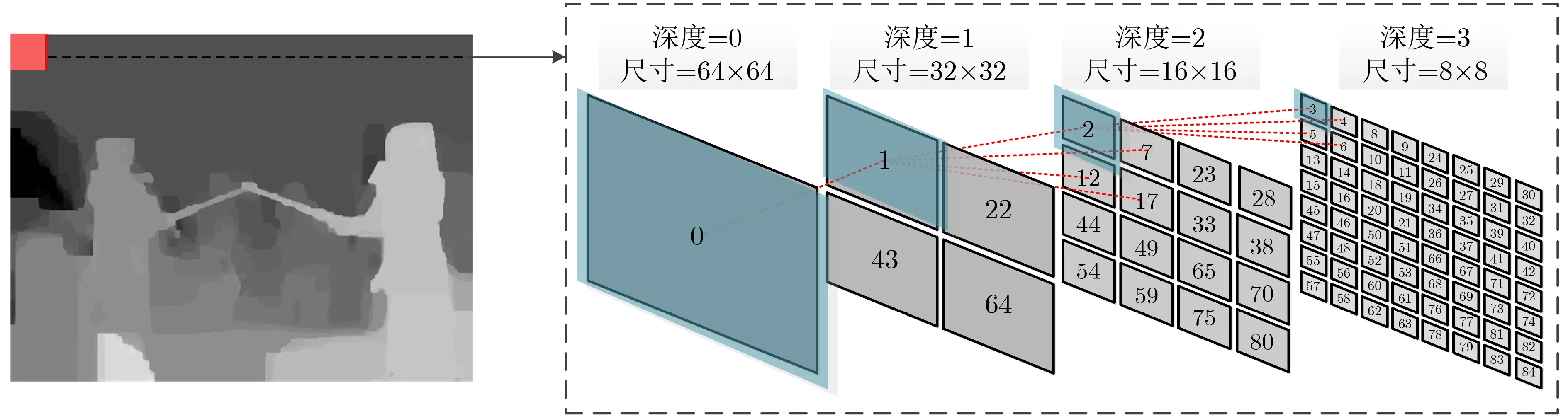
图3 深度图中CTU的四叉树划分过程

据统计，深度图编码单元划分的复杂度占深度图编码复杂度的90%以上[20]。对于一个64×64大小的CTU，采用全遍历模式，完成编码共需要进行85次CU运算，1935次残差变换绝对值和(Sum of Absolute Transformed Difference, SATD)代价运算和至少2623次RD-cost运算。因此，有必要降低3D-HEVC中深度图编码单元划分的复杂度。

3 深度图帧内编码单元快速划分方案

3.1 研究动机

图4展示了编码后深度图中CTU的划分结构以及编码单元纹理复杂度和编码单元深度之间的关系。从图4可看出，在简单、光滑的纹理区域，编码深度通常为0和1；在复杂、粗糙的纹理区域，编码深度通常为2和3。

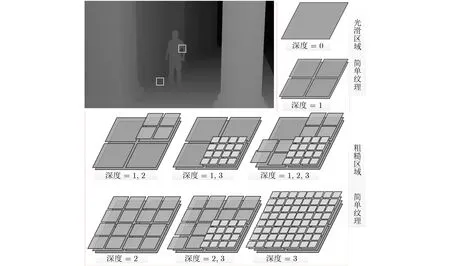
图4 编码单元纹理复杂度和编码单元深度之间的关系

此外，本文还进一步统计了编码单元划分深度和量化参数(Quantization Parameter, QP)之间的关系。如表1所示，初步实验结果表明，采用较小QP值编码后的视频序列倾向于使用大深度、小尺寸CU，采用较大QP值编码后的视频序列倾向于使用小深度、大尺寸CU。其中，QP可以反映编码压缩的情况，QP与量化步长Qstep之间的关系如式(1)所示

表1 编码单元深度和QP的关系(%)

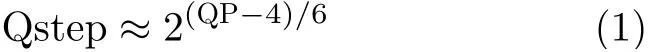
QP越大，Qstep的值越大，量化程度越粗糙，图像失真的情况越严重。相反，QP越小，Qstep的值越小，量化程度越细腻，图像失真的情况越轻微。

基于上述分析发现，如果能直接预测编码单元的划分结构，合理跳过或提前终止某些非必要深度下的率失真代价计算过程，即通过纹理分析直接确定当前深度图CTU的划分结构，可以有效地降低编码时间。因此，如何将深度学习与3D-HEVC编码框架结合，通过网络自动分析CU的纹理复杂度，确定当前编码单元的划分结构，对于解决CU划分复杂度过高这一问题具有重要的参考意义。

3.2 数据集构建

数据驱动深度模型，数据集的种类和数量会对深度模型的性能产生巨大影响。考虑到目前不存在由深度图构成的数据集，为保证实验的准确性，本文从标准测试视频序列中选择了6个不同内容的视频序列，用于构建数据集。其中，包含3个分辨率为1024×768的视频序列以及3个分辨率为1920×1088的视频序列。此外，鉴于不同位置的视点具有内容差异性，本文选择独立视点对应的深度图来构建数据集。

表2展示了本文构建的数据集。如表2所示，训练集由视频序列Kendo的前300帧以及GT_Fly的前250帧组成；验证集由视频序列Balloons的后10帧以及Poznan_Hall2的后10帧组成；测试集由视频序列Newspaper的后20帧以及Undo_Dancer的后20帧组成。然后，所有的视频帧均在3D-HEVC的测试平台HTM16.0[21]下进行编码。编码后，可获得所有编码单元的划分结构和划分深度。将每个编码单元及其对应的划分深度(0～3)作为一个训练样本。在本文构建的数据集中，共包含206160个样本。表3给出了一个样本的具体组成形式。

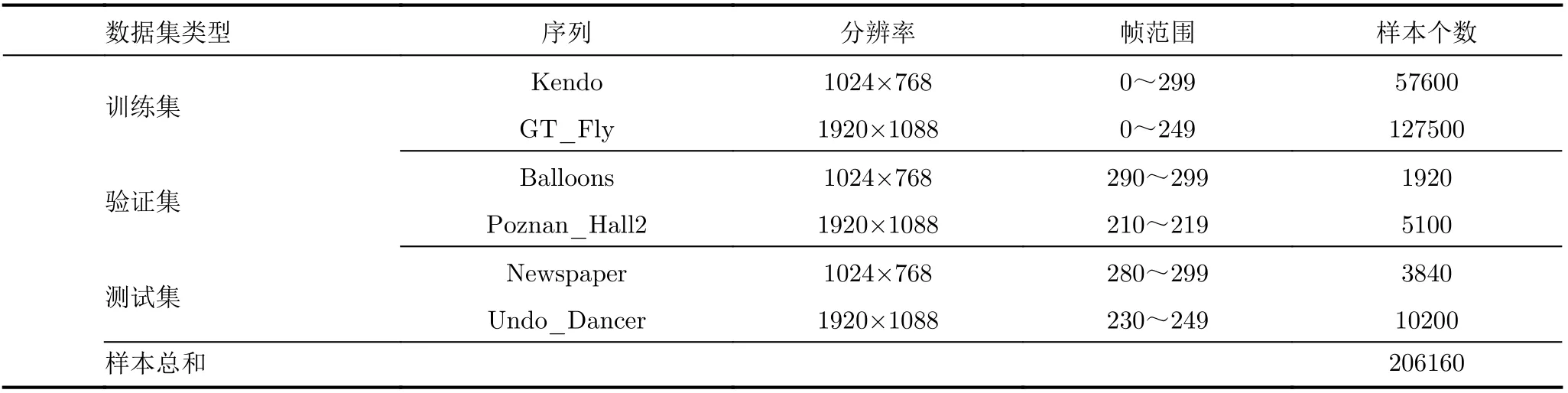
表2 本文构建的数据集

3.3 基于多分支网络的深度模型构建

为直接预测深度图中编码单元的划分结构，本文构建了如图5所示的基于多分支网络的深度模型(Multi Branch CNN, MB-CNN)。该模型包含3个通道，自上向下依次对应“深度=0”(尺寸为64×64)，“深度=1”(尺寸为32×32)，“深度=2”(尺寸为16×16)。模型的输入为独立视点对应深度图中的CTU，尺寸为64×64。模型的输出表示当前深度CU向下划分的概率值。此外，该模型中，小深度、大尺寸CU的划分与否直接决定下一深度CU的划分。下面对模型的结构进行详细介绍。

图5 MB-CNN模型架构图

MB-CNN模型由3个预处理模块、3组卷积层、4个合并层以及3组全连接层组成。具体而言，为了让模型的输出形式与表3的最终划分结构相一致，需要对输入模型的编码单元进行预处理操作。模块A、模块B和模块C均为模型的预处理模块，经3个预处理模块处理后的编码单元大小分别为16×16,32×32和64×64，输入模型的CTU按照模块A、模块B和模块C的顺序逐通道进行预处理。此外，为减少特征维度和干扰信息，模型的预处理模块均采用了平均池化。为从预处理后的CTU中提取边缘特征，卷积层采用的激活函数是线性整流函数(Rectified Linear Unit, ReLU)，可用式(2)来表示

表3 训练样本的组成形式

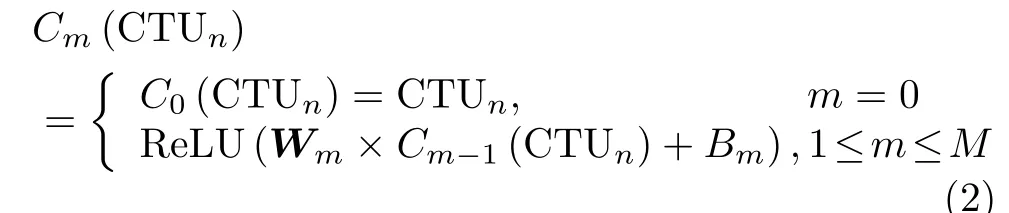
其中，Cm表示预处理模块后的卷积层，M为卷积层的总层数，m表示当前处理的是第几层，n表示当前处理的是第几个CTU，Wm为 权值矩阵，Bm为偏置量。

模型中预处理模块后的卷积操作只是对预处理后的CTU进行逐层特征变换，自动学习各个通道的层次化特征，但其并未考虑到通道间及卷积层间特征的相关性。鉴于此，第2组卷积层和第3组卷积层处理后的特征会先送入到合并层，再经全连接层来学习不同通道、不同层级特征之间的相关性。通过3.1节的表1可看出，QP对CU深度的选择具有重要影响，因此，本文在模型的第2组全连接层中引入QP这一外部特征。此外，考虑到模型的输出是二分类问题，即用0和1表示CU是否划分。因此，模型最后一层采用的激活函数是sigmoid。

在训练MB-CNN时，考虑到其是一个端到端的模型，故可对模型中的各个模块进行联合训练。为了更好地训练MB-CNN，通过整合预测CU是否划分的先验信息以及模型输出的二值化信息，考虑到二值交叉熵损失函数常用于分类问题中，而本文所提模型本质上就是一个二分类问题，故本文将二值交叉熵损失函数作为MB-CNN模型的损失函数，用于本文MB-CNN模型的协同训练。损失函数L定义为

3.4 深度图帧内编码单元快速划分算法

图6展示了本文提出的基于多分支网络的深度图帧内编码单元快速划分算法流程图。首先，读取待编码视频序列，并在编码独立视点对应的深度图时调用MB-CNN模型；其次，读取待编码CTU，并利用MB-CNN模型预测CTU的划分结构；最后，获得最优的CTU划分结构。值得注意的是，在编码过程中，MB-CNN模型的运行只占用了0.5%的编码时间，进一步证明了利用MB-CNN实现CTU划分结构快速预测的可行性。

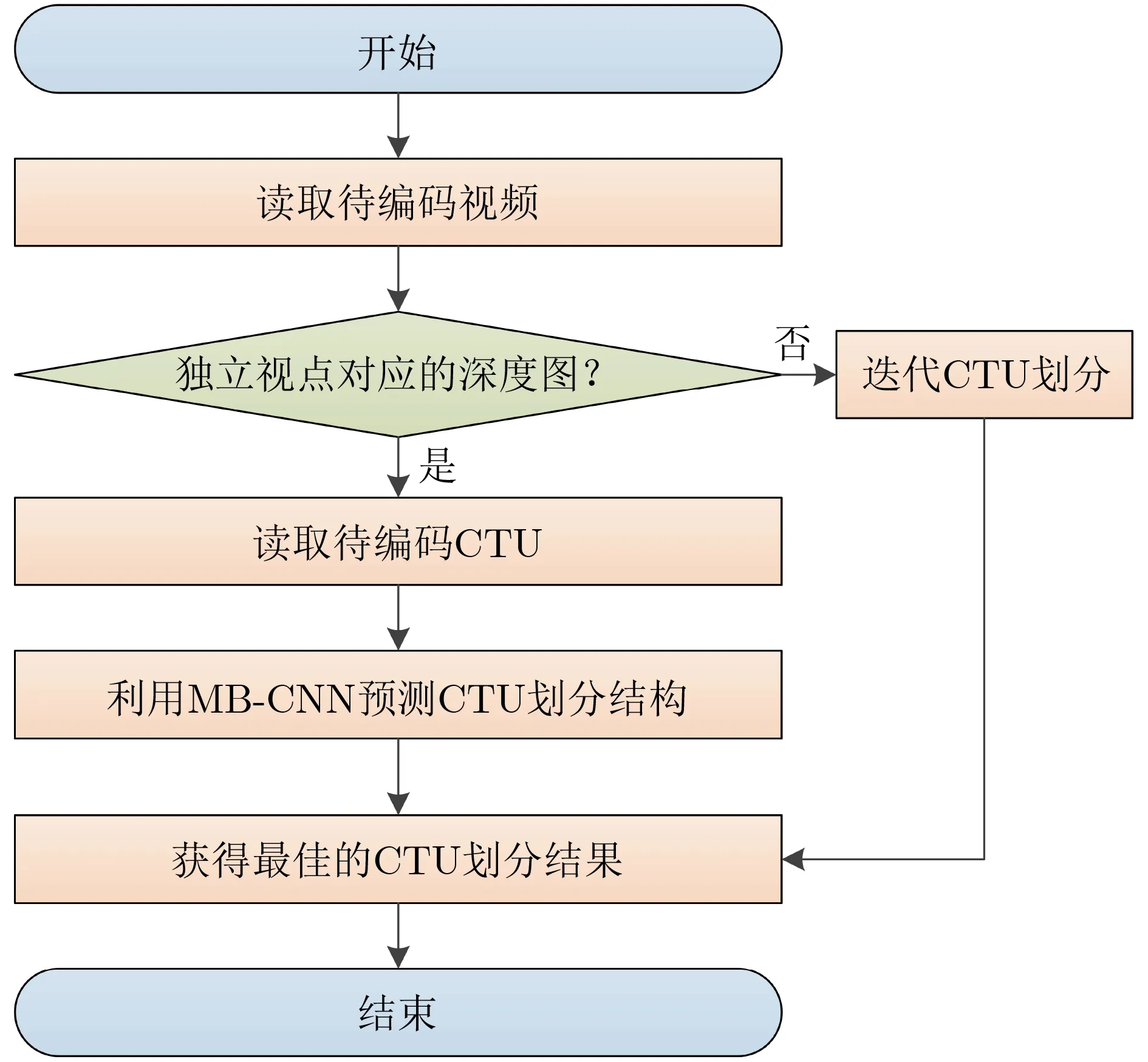
图6 深度图帧内编码单元快速划分流程图

4 实验与结果讨论

4.1 训练环境与编码配置

4.1.1 训练环境

为了验证所提MB-CNN模型的性能，需要先训练提出的MB-CNN模型。模型的训练对实验环境要求较高，需要较强的数据处理能力以提升训练速度。本文训练模型使用的硬件环境及软件环境如表4所示。

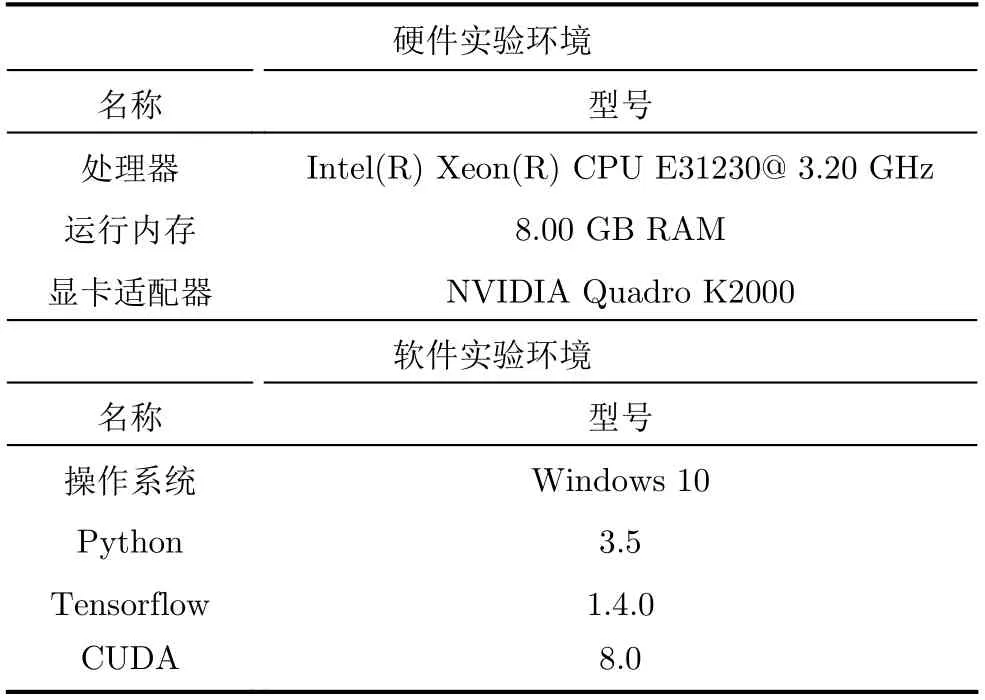
表4 实验环境

在模型的训练过程中，原始输入CTU的尺寸为64×64，“深度=0”、“深度=1”、“深度=2”通道预处理后CTU的尺寸分别为64×64, 32×32,16×16。批尺寸设为64，迭代次数设为10000，初始学习率设为0.01。值得注意的是，固定的学习率显得笨拙，太小的学习率收敛速度慢，学习率太大可能得不到最优解。因此，在MB-CNN模型的训练中，选择动态设置学习率，即初始学习率设为0.01，随着学习次数的增加，每4000次迭代，学习率以0.1的速度衰减。

4.1.2 编码配置

为了验证提出的基于多分支网络的深度图帧内编码单元快速划分算法的性能，采用全帧内(All Intra-frame, AI)编码模式在3D-HEVC测试平台HTM16.0上进行测试。编译软件为Visual Studio 2010，配置文件为baseCfg_3view+depth_AllIntra。具体编码配置如表5所示。

表5 编码参数配置

本文实验采用的标准测试序列及其具体参数如表6所示。值得注意的是，MB-CNN模型的训练集来自标准测试序列Kendo和GT_Fly，与本文实验的标准测试序列并无交叉。

表6 标准测试序列及其参数

本文实验以3D-HEVC测试模型HTM16.0为基准，通过式(4)对编码时间的节省情况进行度量

4.2 结果分析与讨论

4.2.1 训练性能评价

模型的训练性能直接决定了本文所提基于多分支网络的深度图帧内编码单元快速划分算法的可行性。图8展示了MB-CNN模型在训练集下预测CU尺寸的准确率。可以看出，随着迭代次数的增加，CU尺寸的预测准确率逐渐增高，并在迭代次数为5000时趋于稳定。此外，从图8可以发现，MB-CNN模型对尺寸为64×64(“深度=0”)的CU有较高的预测准确率，最高时可达到92.18%。这是由于在模型设计过程中，小深度、大尺寸CU的划分与否直接决定了下一深度CU的划分，所以模型更加关注小深度、大尺寸CU的划分预测。但也正是由于其深度小，对于表征矢量的长度需求低，因此预测难度较小，预测准确率就会高。模型较高的预测准确率也使得本文提出的算法在率失真性能上有较好的表现。

图8 不同迭代次数下不同尺寸CU的预测准确率

4.2.2 客观性能评价

与HTM16.0相比，在AI配置下，本文提出的基于多分支网络的深度图帧内编码单元快速划分算法的编码复杂度与率失真性能分别如表7、表8所示。同时，表7也给出了参考文献[10]中的算法、参考文献[12]中的算法、参考文献[16]中的算法与HTM16.0的性能比较结果。所有实验结果均在本文实验环境以及编码参数配置下得出。

为了证明本文算法的普适性，采用了4个没有出现在训练集中的序列进行测试。如表7和表8所示，与HTM16.0相比，本文算法可以在BDBR(synth PSNR /total bitrate)仅增加5.9%的情况下，平均节省37.4%的编码时间。特别是，对于背景基本不变、前景变化缓慢的序列而言，如Newspaper视频序列，会节省更多的编码时间，Newspaper序列的时间节省率达到了45.3%。

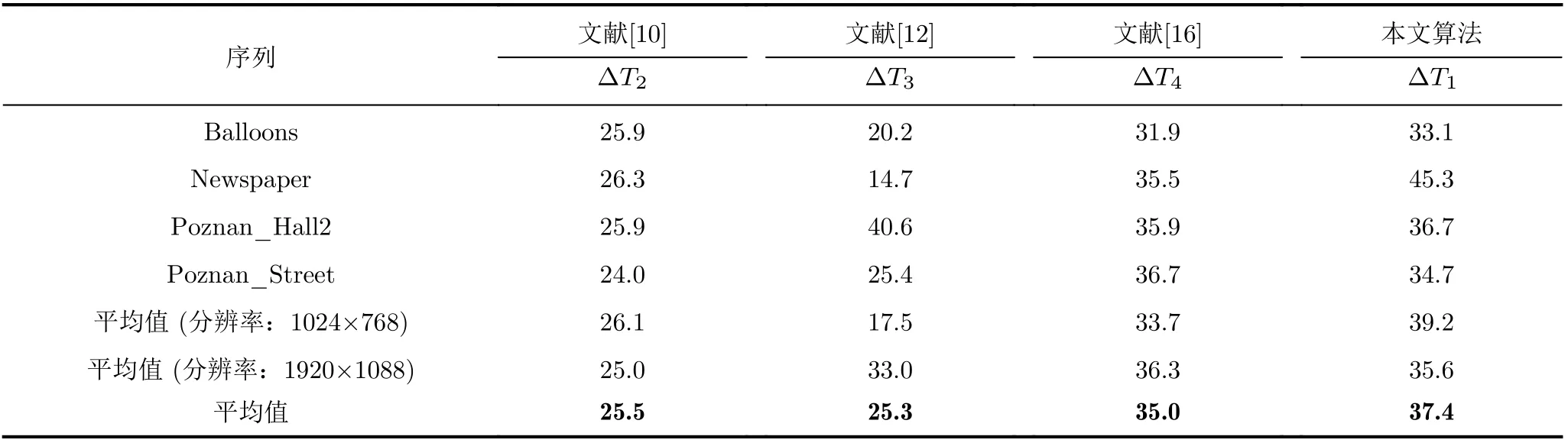
表7 本文算法、参考文献算法与HTM16.0的时间节省比较(%)

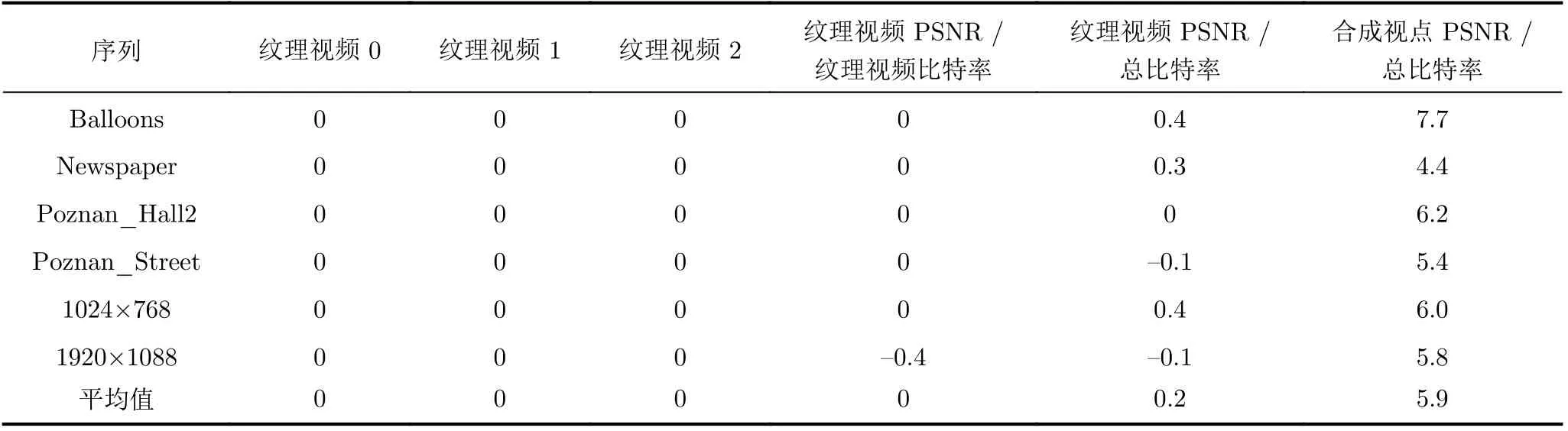
表8 本文算法与HTM16.0的率失真性能比较(%)

为了进一步评估本文算法的性能，分别与文献[10,12,16]进行对比实验。在率失真性能损失较小的情况下，本文算法较参考文献[10,12,16]分别节省了11.9%, 12.1%和2.4%的编码时间。

4.2.3 主观质量评价

为证明本文所提算法能在降低编码复杂度的同时，保证编码后的合成视点质量基本不变。图9以Poznan_Hall2视频序列为例，展示了本文算法与原始HTM16.0方法在编码后合成视点主观质量上的对比。

从图9可看出，与HTM16.0相比，本文算法在主观上并不会造成合成视点质量的明显下降，进一步证明本文算法能在保证合成视点质量基本不变的前提下，降低3D-HEVC的编码复杂度。

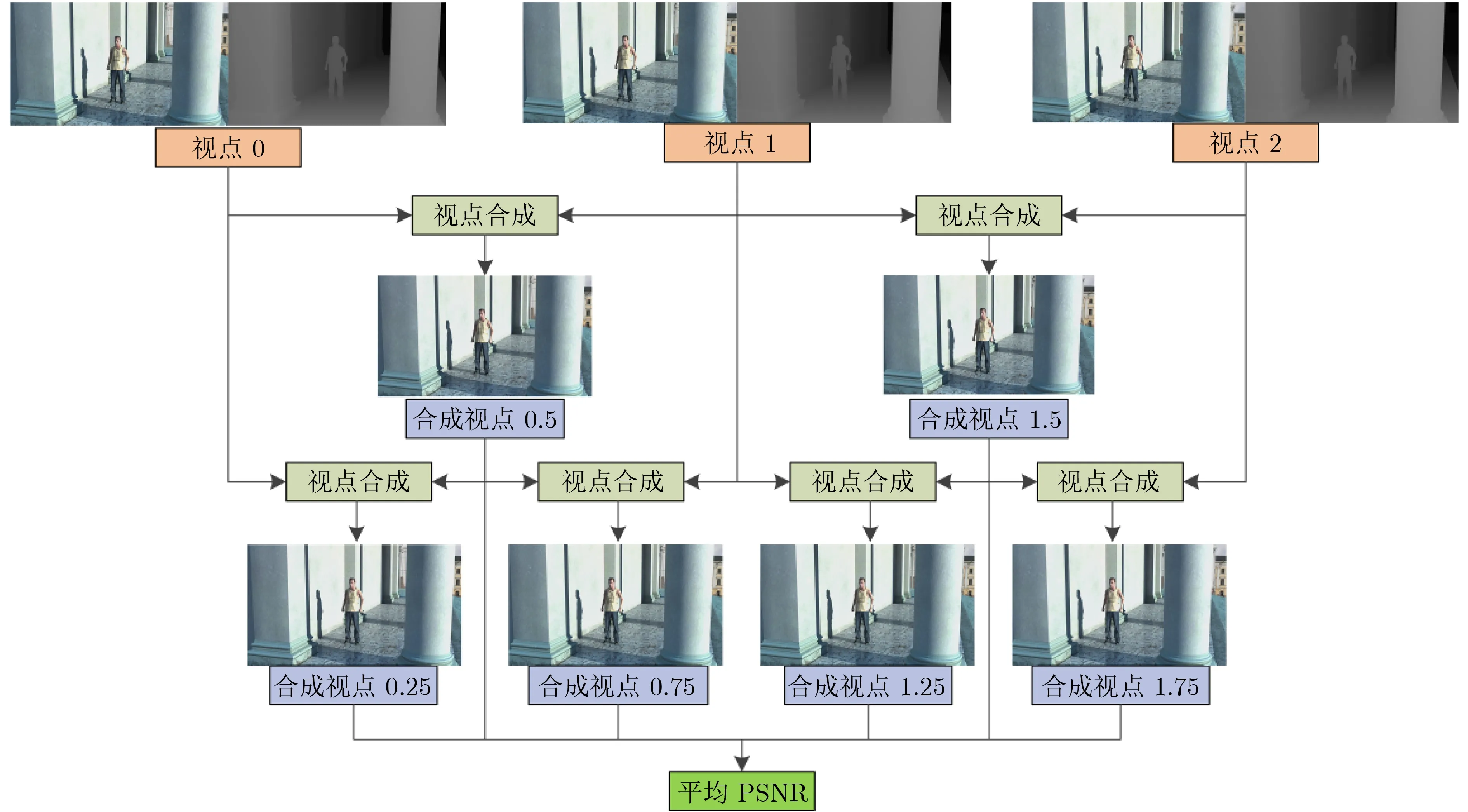
图7 合成视点PSNR的计算过程示意图

图9 Poznan_Hall2视频序列在合成视点0.25上的主观质量对比

5 结束语

本文针对3D-HEVC中深度图帧内编码单元的四叉树划分复杂度过高的问题，提出一种基于多分支网络的深度图帧内编码单元快速划分算法，以降低3D-HEVC的编码复杂度，节省编码时间。通过分析编码单元纹理复杂度和编码单元深度之间的关系，本文所提算法尝试在不进行率失真代价计算的前提下直接预测CTU的划分结构。首先，构建了由独立视点对应深度图中的CTU组成的数据集。其次，提出MB-CNN模型，利用构建的数据集对其进行训练，以实现原始输入CTU的自动分析，直接预测CTU的划分结构。最后，将MB-CNN模型嵌入到3D-HEVC的测试平台HTM16.0中，以确定深度图中最优的CTU划分结构。当利用本文提出算法替代耗时的RDO全遍历搜索时，该算法成功克服了已有算法中依赖人工统计信息来预测编码单元划分深度的缺陷。实验结果表明，与HTM16.0相比，本文所提算法可在BDBR仅增加5.9%、合成视点质量基本不变的前提下，平均降低37.4%的编码复杂度。