基于多时间服务器的时控性加密体制研究

袁 科 程自伟 杨龙威 闫永航 贾春福*③ 何 源

①(河南大学计算机与信息工程学院 开封 475004)

②(河南省空间信息处理工程研究中心 开封 475004)

③(南开大学网络空间安全学院 天津 300350)

④(河南大学国际教育学院 郑州 450046)

1 引言

现实生活中，存在着许多类似的应用场景：发送方完成消息的加密操作，并提前发送给接收方，但接收方只能在未来指定的时间解密，比如密封投标、影视作品定期上映等。如何为这些具有时间特性的应用场景提供安全解决方案？具有“向未来发送消息”特性的密码原语，即时控性加密[1](Timed-Release Encryption, TRE)技术可以解决这一问题。TRE是一种融入时间因素的密码学技术，密文只能在未来时间被解密，并且能够与已有应用问题的密码学方案进行结合，为其提供时间特性。

最新研究表明，尽管目前TRE构造已经扩展到物理方法[2,3]和区块链技术[4–6]，但TRE构造方案大多数仍然都是基于数学问题[1,7–16]，比如基于双线性迪菲·赫尔曼(Bilinear Diffie-Hellman, BDH)问题、基于双线性迪菲·赫尔曼可逆(Bilinear Diffie-Hellman Inversion, BDHI)问题、基于双线性迪菲·赫尔曼指数(Bilinear Diffie-Hellman Exponent,BDHE)问题。TRE技术最早由May[6]提出，早期的TRE方案通过解决某些特定规模的非并行计算问题，比如基于因式分解困难问题[1,17]，但暴露的无法准时解密问题亟需研究者解决。为了解决接收方能够准时解密的问题，研究者的重点主要集中在代理方法上。即在TRE方案中考虑引入一个第三方实体，也称为时间服务器[11]，可以为接收方提供一个精确的公开时间参考。时间服务器方式分为交互式和非交互式两种。在交互式时间服务器方式中，当TRE系统用户增多时，时间服务器可能会面临遭受拒绝服务攻击[18]的安全风险。此外，基于交互式时间服务器方式构造的TRE方案解密工作需要和时间服务器完成双向交互通信过程，可能会泄露发送方[1]、接收方[11]或消息相关的隐私信息。

为了解决交互式时间服务器方式的隐私泄露问题，非交互式时间服务器方式为进一步研究的目标。非交互式时间服务器方案初始基于2次剩余问题[19]构造，消息的安全性依赖于时间服务器，该方案抵抗攻击能力较弱。后续的基于非交互式时间服务器TRE方案，解密工作需要具备时间陷门(时间服务器对解密时间进行“类似加密”操作所得[20])和私钥(接收方拥有)才能完成。但是TRE方案均依赖单一时间服务器发布的时间陷门进行解密，假设时间服务器遭到攻击者/不诚实的接收方的腐败，提前非法获取时间陷门解密，那么就无法确保消息的机密性，而容易凸现一定的安全隐患。

针对上述问题，本文重新审视基于非交互式时间服务器方式构造的TRE模型，将时间服务器数量由1个增加到N个，并构造一种简单高效的基于BDH问题的可证明安全的多时间服务器(Multiple Time Servers TRE, MTSTRE)方案。在多时间服务器的场景下，对不诚实的接收方而言，需要腐败全部的时间服务器，而不是仅仅只需腐败一个时间服务器就可以解密。类似地，对攻击者而言，本文不考虑其是否已经获取到合法接收方的私钥情况，主要考虑获取时间陷门方面。如果适当设置时间服务器数量N值，N值越大，不诚实的接收方/攻击者所需考虑的贿赂成本也越大。

因此，相对于单时间服务器TRE方案来说，MTSTRE方案的安全性更强。但已有多时间服务器Chan等人[9]、Hristu-Varsakelis等人[10]的TRE方案既没有给出安全性分析，也没有给出相关的可证明安全的证明。为此，本文将给出所提方案是抗不可区分、发布时间可选、自适应选择明文攻击(INDistinguishable, selective release Time, adaptive Chosen-Plaintext Attack, IND-sT-CPA)的安全性证明。

2 基础知识

定义1有限域上的离散对数问题(Discrete Logarithm Problem, DLP)。假设p,q为两个素数，G2={gk:0≤k ≤q −1}为 素 域Zp上 阶 为q的 循 环乘法群，g为G2中的一个生成元。如果给定元素y ∈G2， 求解整数x∈Zq使得y=gx的问题，称为有限域上的离散对数问题。

定义2有限域椭圆曲线上的离散对数问题(Elliptic Curve Discrete Logarithm Problem,ECDLP)。假设p,q为两个素数，G1={nα:0≤n ≤q −1}为椭圆曲线群上的一个q阶子群，α为G1中的一个生成元。如果给定元素β ∈G1， 求解整数x∈Zq使得β=xα的问题，称为有限域椭圆曲线上的离散对数问题。

定义3 双线性对。假设G1为有限域椭圆曲线上的循环加法群，G2为有限域上的循环乘法群，G1,G2群 阶均为素数q。使用双线性对技术，可以将有限域椭圆曲线上的循环加法群的困难问题规约为有限域上的循环乘法群的困难问题。双线性映射为e:G1×G1→G2，满足：

(1)双线性性质。对于任意P,Q,R ∈G1，有：e(P+Q,R)=e(P,R)e(Q,R),e(P,Q+R) =e(P,Q)e(P,R)。

(2)非退化性。如果g是G1的生成元，则e(g,g)是G2的生成元。

(3)可计算性。对于任意的P,Q ∈G1，存在有效计算e(P,Q)的算法。

3 模型定义

3.1 系统模型

本方案的系统模型如图1所示，包含的参与实体有发送方、N个时间服务器和接收方。发送方设置指定的解密时间T，对机密文件M加密并提前将对应的密文C发送给接收方。在指定的解密时间T到来时，N个时间服务器会周期性地发布各自的时间陷门。在指定的解密时间T时，接收方获得N个时间服务器的时间陷门，再结合自己私钥生成的时间陷门来解密密文C。

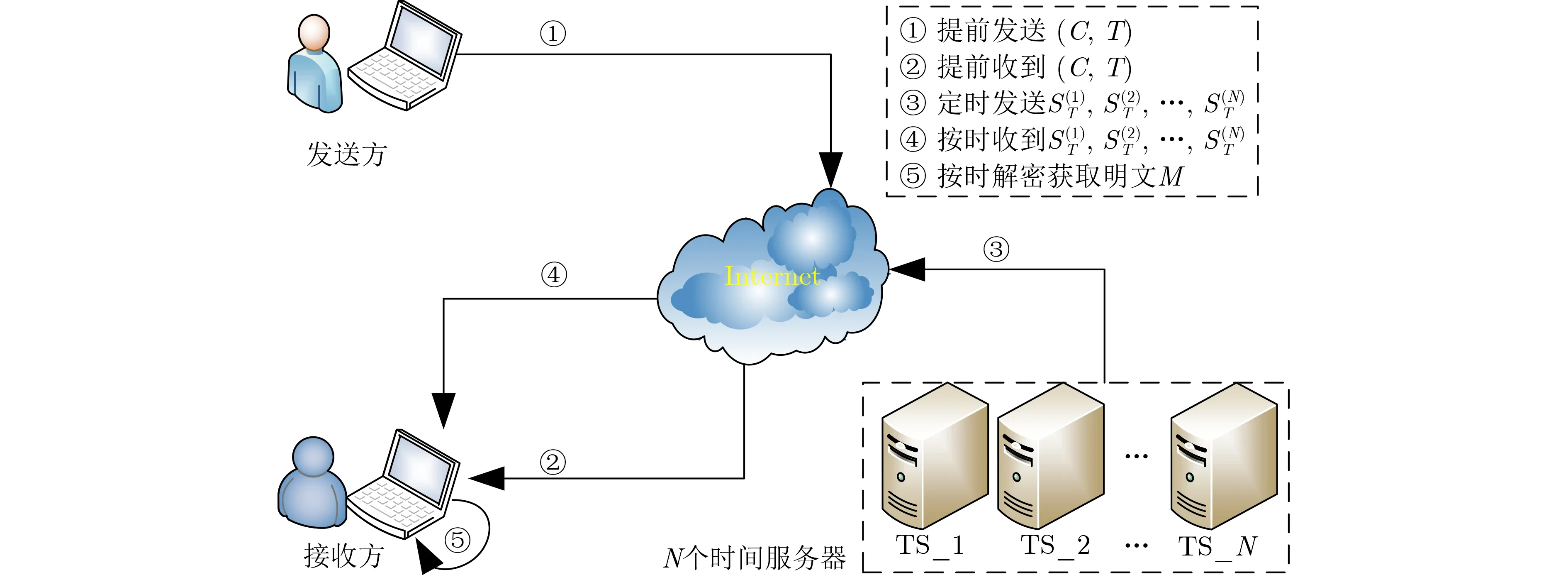
图1 系统模型

3.2 算法组成

3.3 安全模型

4 MTSTRE具体方案

4.1 方案描述

4.2 安全性证明

本节给出上述基于随机预言机模型的MTSTRE方案是抗自适应选择明文攻击的语义安全证明。

4.3 效率分析

如果系统用户(接收方)无法正常解密时，可以通过计算各个双线性对运算值e(siP,H1(T))和相应的e(P,siH1(T)) 是 否相等，其中1≤i ≤N，来验证哪一个时间服务器的时间陷门出现问题。而Chan等人[9]方案设计不同，在解密时都必须首先验证时间服务器的时间陷门真实性，因此，效率较低。MTSTRE方案与Chan等人[9]方案和Hristu-Varsakelis等人[10]方案进行效率对比，如表2所示。

由表2可以看出，在Chan等人[9]方案中，完成整个加解密过程的计算成本相对较高。相比之下，MTSTRE方案比Hristu-Varsakelis等人[10]方案的计算效率略有提高。

表2 多时间服务器TRE方案相对耗时表

以TRE典型应用场景–密封投标为例说明实际应用场景中的效率情况。假设招标方A对某一项目进行招标，规定在“2023年1月1日上午8点整”开标，5个投标方(B1,B2,B3,B4,B5)参与投标，并设置时间服务器的数目为10个。为确保本次参与竞标的公平性以及5个投标方标书的安全性，招标方A采用本文所提的MTSTRE方案。同样采用表1中相对耗时的统计方法，那么，在Enc阶段，总计算成本为31.304。在TS_Rel阶段，总计算成本为1.3214。在Dec阶段，总计算成本为19.697，如表3所示。

表1 其他基本运算相对于PMec运算的相对耗时统计表

表3 密封投标应用场景相对耗时统计表(PMT)

5 MTSTRE通用方案

5.1 形式化定义

本节将通用公钥加密GPKE方案[20]与MTSTRE方案进行结合，并且给出如下定义7通用多时间服务器时控性加密(Generic MTSTRE, GMTSTRE)方案的形式化定义。

定义7 GMTSTRE方案由发送方、接收方和N个时间服务器组成，涉及的算法6元组表示为ζGMTSTRE={Setup,TS_KeyGen,User_KeyGen,En c,TS_Rel,Dec}，具体如下：

Setup(1λ)是一种初始化的概率算法。输入安全参数λ，生成系统通用的公共参数p arams。

5.2 方案构造

在GMTSTRE方案形式化定义的基础上，给出相应的构造方法，过程如下：

6 结束语

为了解决目前基于非交互式时间服务器方式构造的TRE方案依赖于单时间服务器进行解密的安全问题，本文提出一种简单高效的多时间服务器TRE方案MTSTRE。在指定解密时间时，多个时间服务器计算并发布时间陷门，用户使用所有的时间陷门来完成解密工作。效率分析表明，与已有最有效的多时间服务器TRE方案相比，所提具体方案效率略高，且本文给出了严格抗自适应选择明文攻击的安全性证明。

本文所提方案还存在一些问题有待解决，比如如何确保多时间服务器TRE模型的实用性更强，避免少量时间服务器出现宕机等故障而拒绝发布时间陷门。因此，后续工作将继续探索TRE和其他密码技术的组合使用，构造用户身份信息对时间服务器匿名和具有鲁棒性的多时间服务器TRE模型。