一种多传感器自适应量测迭代更新GM-PHD跟踪算法

申屠晗 李凯斌 荣英佼 李彦欣 郭云飞

①(杭州电子科技大学自动化学院 杭州 310018)

②(近地面探测技术重点实验室 无锡 214035)

1 引言

目标跟踪指利用传感器观测数据对未知目标的数量和状态进行贝叶斯后验估计的过程。在实际应用中，目标跟踪问题面临诸多难点[1]，主要包括：(1)目标数量不确定且时变；(2)传感器观测数据存在漏检、虚警和观测误差等。在一些复杂跟踪环境下，仅利用单传感器观测数据进行目标跟踪，面临数据不足导致跟踪效果不佳的问题。此时，可通过多传感器数据融合来提升效果[2]，其主要优势是利用多传感器的信息冗余[3]来克服单传感器数据的匮乏性。

基于数据关联的多传感器多目标跟踪方法在进行跟踪滤波前需要解决数据关联问题，典型跟踪方法包括：最近邻方法(Nearest Neighbor, NN)[4]、概率数据关联方法(Probabilistic Data Association,PDA)[5,6]、联合概率数据关联方法(Joint Probabilistic Data Association, JPDA)[7,8]、多假设方法(Multiple Hypothesis Tracking, MHT)[9,10]等。除了数据关联类的跟踪方法，基于随机有限集(Random Finite Set, RFS)[11]的方法可以在隐式建模关联测度的基础上直接解决状态估计问题，使数据关联结果不再作为跟踪滤波的前置条件。典型跟踪方法包括：概率假设密度(Probability Hypothesis Density, PHD)跟踪器[12]和势概率假设密度(Cardinalized PHD, CPHD)跟踪器[13]等。为了便于工程应用，PHD跟踪器有两种常见的近似算法，一种是基于高斯混合(Gaussian Mixture, GM)模型的GM-PHD跟踪算法[14]，另一种是基于序贯蒙特卡罗(Sequential Monte Carlo, SMC)的SMC-PHD跟踪算法[15]。SMC-PHD可以获得比较高的跟踪精度，代价是更多的计算消耗。GM-PHD在精度和计算消耗之间进行了折中，拥有较好的费效比。将单传感器GM-PHD推广至多传感器跟踪场景，常见的跟踪方法包括：基于点迹融合的跟踪方法和基于序贯更新融合的跟踪方法等[16–19]。基于点迹融合的跟踪方法主要通过多传感器点迹PHD融合的方式实现联合跟踪[16]。基于序贯更新融合的跟踪方法则通过序贯的方式对多传感器PHD信息进行迭代滤波融合[17–19]。基于点迹融合的跟踪方法更加容易兼容于多种形式(集中式、分布式、分散式、混合式等)的多传感器跟踪网络；基于序贯更新融合的跟踪方法可在以集中式融合为代表的多传感器跟踪网络中获得更高精度的跟踪结果。

尽管多传感器序贯更新融合PHD算法可以获得较好的跟踪效果，但是研究表明其融合结果对融合顺序是敏感的[20,21]。Nagappa等人[22]较早指出了多传感器PHD迭代更新融合时的顺序敏感问题。融合结果顺序敏感实际上是由于传感器观测数据的质量不同所导致的结果，如果所有传感器的检测概率都一样，那么融合结果与顺序无关；当各传感器的检测概率不同时，融合结果就会出现顺序敏感现象。Liu等人[23,24]也提到不同的传感器更新顺序会得到不同的跟踪结果。

因为当传感器质量不同时，基于量测迭代更新的PHD融合跟踪算法是顺序敏感的，所以研究能够自适应优化融合顺序的融合跟踪算法是必要的。一个难点在于，实际应用时一般没有先验信息来说明各个传感器实时工作时所提供的数据的质量。因此需要解决多传感数据质量的在线评估和顺序优化问题。提出一种多传感器自适应量测迭代更新GMPHD(multi-sensor Adaptive observation Iteratively Updating GM-PHD, AIU-GM-PHD)跟踪算法。首先，将单传感器GM-PHD算法进行扩展，构建多传感器自适应量测迭代更新融合框架；其次，基于最优次模式分配 (Optimal Sub-patten Assignment, OSPA)度量提出一种多传感器融合一致性度量方法；最后，通过各传感器一致性度量的大小排序进行量测迭代更新融合，从而构建AIU-GM-PHD算法。为进一步提高目标跟踪精度，提出一种带权伪量测的多传感器自适应迭代更新GM-PHD(Weighted Pseudo Observation Multi-sensor Adaptive Iteratively Updating GM-PHD, PAIU-GMPHD)跟踪算法。从各传感器的后验高斯集中提取位置和权重信息作为伪量测代替原始量测进行迭代更新融合。具体而言，由于提取的伪量测已经过一次滤波和数量压缩处理，所以具备提高跟踪精度和降低计算负担的潜力。

2 问题描述

假设k时刻有Nk个目标，Nk是未知且时变的。目标i的状态向量为xk,i=[xi,x˙i,yi,y˙i]T，xi,yi表示目标的位置，x˙i,y˙i表 示目标的速度。Nk个目标的状态向量集为Xk={xk,1,xk,2,...,xk,Nk}。对于任意目标i， 如果在k−1和k时刻都存在，则状态转移方程为

其中，F为状态转移矩阵，vk为目标过程噪声，服从均值为0，协方差为Qk的高斯随机过程。

假设有L个传感器，对于任意传感器j，在k时刻以检测概率0≤pd ≤1 对目标i形成观测

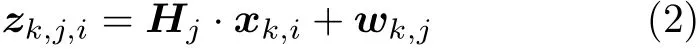
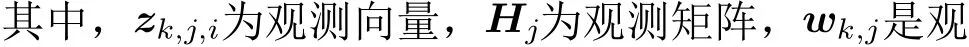
本文的研究目标是利用多传感器的量测信息实现对观测空间目标数量和状态的跟踪估计，即在式(1)–式(3)已知的条件下，利用Z1:k对Xk进行后验估计，需要着重解决多传感器观测数据质量的在线评估和多传感器迭代融合顺序的优化问题。如果存在通信延迟，可以利用量测数据的外推技术处理[25]。

3 多传感器量测迭代更新GM-PHD跟踪算法

问题描述中给出的是多传感器多目标跟踪的问题，该问题的单传感器跟踪版本是可以利用GM-PHD算法来解决的[13]。本文将提出的多传感器GM-PHD跟踪算法是在单传感器GM-PHD算法的基础上构建的。因此，为方便讨论，本节简要回顾GM-PHD算法和量测迭代更新GM-PHD跟踪算法的主要结论[14,17]。

3.1 GM-PHD跟踪算法

3.2 量测迭代更新GM-PHD跟踪算法

基于上述GM-PHD滤波方法，存在多个传感器时，依次利用各传感器的量测信息对混合高斯集进行迭代更新，得到量测更新GM-PHD跟踪算法流程如图1所示。假设在k−1 时刻的后验PHD估计由式(12)描述

图1 GM-PHD量测迭代更新流程图

4 多传感器自适应量测迭代更新GM-PHD跟踪算法

针对多传感器融合结果对融合顺序是敏感的[26]这个问题，本节首先提出一种全局OSPA一致性度量来在线评估各传感器估计信息的质量，然后构建一种多传感器自适应量测迭代更新GM-PHD(AIUGM-PHD)跟踪算法。从而解决多传感器GM-PHD迭代更新时融合顺序的在线优化问题。

4.1 全局OSPA一致性度量

这里假设大多数传感器的数据是有效的，那么某个传感器的后验GM集与所有其他传感器的后验GM集的一致性距离之和越小，则说明该传感器处于“较好状态”。所以全局OSPA越小，传感器数据质量越高。

4.2 全局OSPA一致性度量AIU-GM-PHD跟踪算法

AIU-GM-PHD跟踪算法的融合策略是按照全局OSPA一致性度量从大到小迭代融合各传感器数据，即先将GM集质量较低的传感器进行融合，质量较好的放在之后进行融合。AIU-GM-PHD融合框架如图2所示。

图2 AIU-GM-PHD算法框架图

为简便记，将AIU-GM-PHD跟踪算法的核心步骤归整如下：

步骤2 预测更新。各传感器利用自身量测根据式(4)和式(7)进行预测更新，得到各自的后验GM集。

步骤3 用式(16)和式(18)计算每个传感器的全局OSPA，并从大到小对各传感器进行融合顺序排序。

步骤4 进行量测迭代融合。根据步骤3得到的融合顺序，以OSPA最大的传感器所对应的后验GM集为起点利用式(12)–式(15)进行迭代更新融合，每次迭代更新后可进行一定的剪枝合并处理。

5 多传感器自适应带权伪量测迭代更新GM-PHD跟踪算法

6 仿真分析

实验1 为验证量测迭代更新GM-PHD跟踪算法的融合顺序对融合结果的影响，实验设置见表1，其中pid表 示传感器i的 目标检测概率，λi表示传感器i的 杂波数量强度(泊松分布强度)，i=1,2,3,4。

表1 实验1场景设置

在实验1的场景1中根据检测概率大小进行排序(认为检测概率大的观测质量较好)，对比正反两种顺序的融合结果，顺序 1→2→3→4表示从较好到较差，顺序 4→3→2→1表示从较差到较好。由图3可知，在各传感器检测概率不同，杂波强度相同的场景下，融合顺序对检测概率的敏感度高。

图3 场景1两种融合顺序的OSPA对比图和目标数目估计对比图

在实验1的场景2中根据杂波强度大小进行排序(认为杂波强度小的观测质量好)，对比正反两种顺序的融合结果，顺序 1→2→3→4表示从较好到较差，顺序 4→3→2→1表示从较差到较好。由图4可知，在各传感器检测概率相同，杂波强度不同的场景下，融合顺序对杂波强度的敏感度不高。

图4 场景2两种融合顺序的OSPA对比图和目标数目估计对比图

实验2 将本文所提出的AIU-GM-PHD跟踪算法、PAIU-GM-PHD跟踪算法与单传感器GMPHD跟踪算法、随机融合顺序的多传感器GMPHD量测迭代更新(RIU-GM-PHD)跟踪算法[23]以及MD-IC-PHD跟踪算法[24]进行比较。为了对比检测概率和杂波强度不同情况下各算法的有效性，设置相关参数见表2。

表2 实验2场景设置

在场景1中设置各传感器的检测概率不同，杂波数相同，各算法的OSPA对比如图5(a)所示，目标数目估计如图5(b)所示。

由图5可以看出在各传感器的检测概率不同，杂波强度相同的情况下，与单传感器GM-PHD、RIU-GM-PHD跟踪算法相比，AIU-GM-PHD算法的跟踪精度和目标数目的估计精度更高。但相较于PAIU-GM-PHD算法，AIU-GM-PHD算法的OSPA精度略低。场景1的部分仿真结果如表3所示。

表3 场景1仿真结果

图5 场景1各算法的OSPA对比图和目标数目估计对比图

在场景2中，设置各传感器检测概率相同，杂波数不同，各算法的OSPA对比如图6(a)所示，目标数目估计如图6(b)所示。

由图6可以看出在各传感器的检测概率相同，杂波强度不同的情况下，与单传感器GM-PHD、RIU-GM-PHD跟踪算法相比，AIU-GM-PHD算法的OSPA度量低于RIU-GM-PHD算法的OSPA度量，目标数目的估计精度也较高。但相较于PAIUGM-PHD算法，AIU-GM-PHD算法的OSPA度量高于PAIU-GM-PHD算法的OSPA度量。场景2部分仿真结果如表4所示。

表4 场景2仿真结果

图6 场景2各算法的OSPA对比图和目标数目估计对比图

在场景3中，设置各传感器检测概率和杂波数都不相同，各算法的OSPA对比如图7(a)所示，目标数目估计如图7(b)所示。

由图7可以看出在各传感器的检测概率不同，杂波强度也不同的情况下，与单传感器GM-PHD、RIUGM-PHD跟踪算法相比，AIU-GM-PHD算法的OSPA度量远低于RIU-GM-PHD算法的OSPA度量，目标数目的估计精度也较高。场景3仿真数据如表5所示。

表5 场景3仿真数据

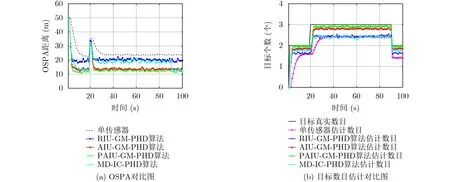
图7 场景3各算法的OSPA对比图和目标数目估计对比图

综合以上3个场景的仿真结果，可以看出本文所提的AIU-GM-PHD算法在检测概率和杂波参数不同的典型场景中的跟踪性能都优于随机顺序融合算法，能够对融合顺序进行一定程度的优化，对比MD-IC-PHD算法，同时提出的PAIU-GM-PHD算法估计精度比提出的AIU-GM-PHD算法高，鲁棒性更好，跟踪结果质量更佳，增加的计算量较小，在实际的工程应用中比较推荐使用PAIU-GM-PHD算法。AIU-GM-PHD算法和PAIU-GM-PHD算法在高杂波、高检测概率的场景中，文献[24]中的MD-IC-PHD算法精度更高，原因是MD-IC-PHD算法采用了增加量测子集属于正确量测子集的权重，从而抑制了会对跟踪效果产生负面影响的部分，传感器本身存在漏检的概率较低，这样既增加了正确的权重，又使得错误量测(杂波)的权重得到了抑制，从而提高了基数(目标数量)估计的精度，所以相比于本文提出的算法，精度偏高；在低杂波、低检测概率和高杂波、低检测概率场景中算法性能优于文献[24]中的MD-IC-PHD算法，原因是传感器的检测概率较低，虽然增加了正确量测子集的权重，但是由于传感器检测概率低，漏检常有发生，因此，增加部分正确量测子集的权重是以进一步放大漏检概率为代价的，这样该方法的整体收益就受到了一定的抑制，导致在这两个场景中的跟踪精度比本文所提方法的跟踪精度稍低。

为分析各算法的计算复杂度，现假设有L个传感器，各传感器的平均目标数估计个数为m个，后验GM集粒子平均个数为j，各传感器的平均量测个数为d。平均目标数估计个数m。3 种迭代更新算法的复杂度分析见表6。

表6 3 种算法时间复杂度对比

7 结束语

本文针对多传感器PHD迭代更新融合算法对融合顺序敏感的问题，提出一种AIU-GM-PHD跟踪算法，同时，为进一步提高跟踪精度，提出一种PAIU-GM-PHD跟踪算法。提出的AIU-GMPHD算法、PAIU-GM-PHD算法可以在线评估各传感器估计结果的相对质量，并推荐采用从相对差到相对好的迭代融合顺序。仿真结果表明，在3 种典型的检测概率和杂波强度不同的多传感器跟踪场景下，与RIU-GM-PHD相比，AIU-GM-PHD算法与PAIU-GM-PHD算法在OSPA和目标数量估计方面都具有更好的跟踪精度，且PAIU-GM-PHD算法的跟踪精度优于AIU-GM-PHD算法。在计算复杂度方面，与RIU-GM-PHD相比，AIU-GM-PHD算法与PAIU-GM-PHD算法额外增加的计算复杂度是线性的，计算复杂度主要体现在迭代更新的过程中。本文所提AIU-GM-PHD算法和PAIU-GMPHD算法是基于待融合传感器中，质量较差的传感器占比较小的前提，所以AIU-GM-PHD算法和PAIU-GM-PHD算法适用于质量较好的传感器占比超过50%的场景。关于怎样确定实际场景中质量较好的传感器所占的比例，以及当前传感器中质量较好的传感器占比不足50%时该如何设计融合策略的问题，可以作为未来的研究方向。