缺口对ML20MnTiB钢拉伸强度的影响研究*

李雨林

宝鸡文理学院 机械工程学院 陕西宝鸡 721016

1 研究背景

ML20MnTiB钢常用于生产10.9级标准件,特点是不需要预先球化退火处理就可直接拉拔和冷镦加工,具有优越的冷变形性能和强韧性,淬火变小,开裂倾向弱,可用水淬处理,脱碳敏感性低。由于性能优异,制造成本较低,可以用于制造汽车主体架构及列车零部件。

笔者对ML20MnTiB钢试样进行拉伸试验,并对试样的拉伸过程进行仿真分析,以此获得试样的真应力对数应变曲线、应力场、应变场,以及载荷分布状态。对各试样的断口处进行电镜扫描,研究并分析缺口对ML20MnTiB钢断裂的作用机理,以及与应力三轴度、塑性应变之间的关系,为后续ML20MnTiB钢的推广使用及失效分析提供理论指导。

2 试验材料

ML20MnTiB钢以少量硼代替大量合金元素,碳和合金元素含量低,因此具有良好的综合力学性能,具体元素含量见表1。

表1 ML20MnTiB钢元素含量

光滑试样和不同尺寸缺口试样尺寸如图1所示。缺口试样的缺口半径分别为16 mm、8 mm、4 mm,为防止夹持端与标距段交汇处应力集中影响试验的准确性,采用圆角过渡。试样参照GB/T 228—2021制作。

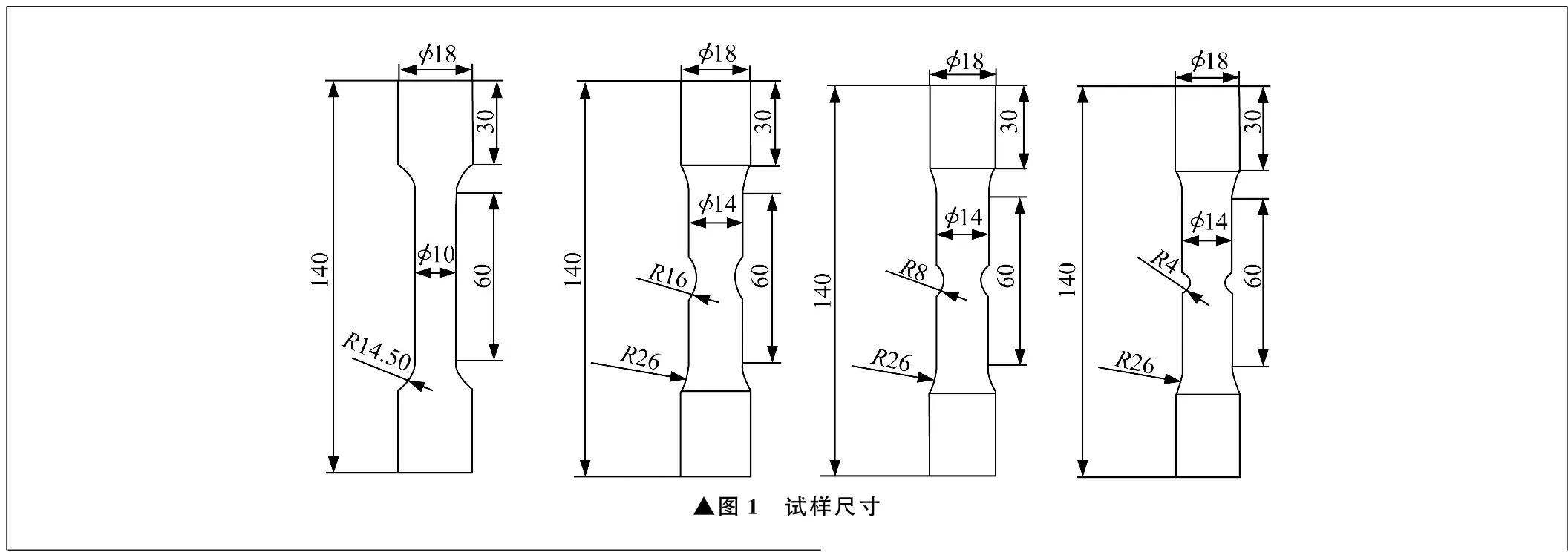
▲图1 试样尺寸

3 试验过程

试验在室温下进行,将ML20MnTiB钢试样在拉伸疲劳试验机上进行拉伸性能试验,试验时拉伸速度为2 mm/min。在试样标距段安装引伸计,引伸计标距为 50 mm。在拉伸试验过程中,分别记录光滑试样及不同尺寸缺口试样加载的试验力位移曲线,对各试样的试验曲线进行拟合。拉伸疲劳试验机如图2所示。

▲图2 拉伸疲劳试验机

笔者根据光滑试样的单轴拉伸试验,得到材料塑性性能曲线和对应的真应力曲线原始数据,真应力应变关系曲线如图3所示。

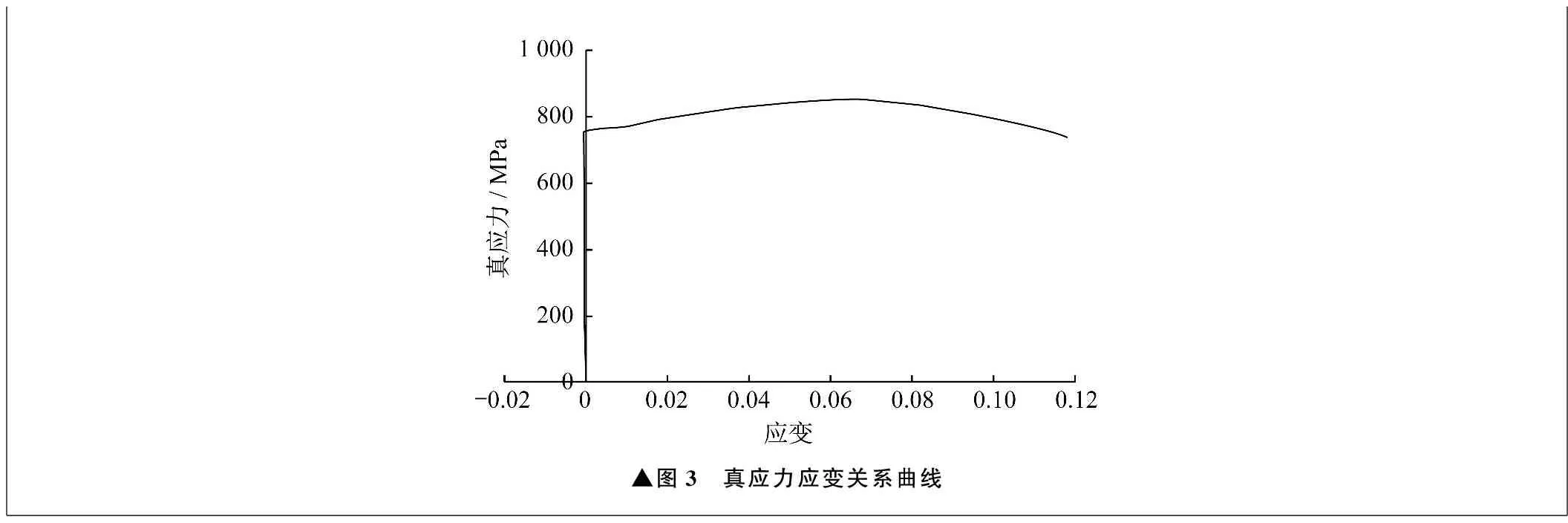
▲图3 真应力应变关系曲线

以光滑试样的本构关系作为缺口试样的本构关系,将本构关系导入Ansys Workbench软件,以试验的拉伸位移、拉伸速度作为仿真约束参数,材料泊松比为0.25,进行拉伸仿真分析。分析过程中采用位移加载方式,位移加载量与试验值一致。由此可以获得试样加载过程中模拟标距段位移、载荷数据,以及拉伸过程中缺口试样的应力三轴度云图,用于分析光滑试样及缺口试样在相同条件下的应力三轴度对断裂失效机理的影响。当有限元模型网格尺寸小于0.1 mm时,网格尺寸对试样失效应变的影响可以忽略。为保证模拟精度,试验中所有试样的有限元模型网格尺寸均取 0.1 mm,在此基础上对试样缺口根部单独进行网格加密。

笔者利用扫描电子显微镜对光滑试样及缺口试样的断裂面进行电镜扫描,从电镜图片中观察试样的断裂面形态及断裂机理。扫描电子显微镜如图4所示。

▲图4 扫描电子显微镜

4 试验结果

4.1 缺口尺寸对拉伸性能影响

试样载荷位移曲线如图5所示。由图5可知,光滑试样和缺口试样的载荷位移曲线拟合程度较好,说明以光滑试样的本构关系及材料性能参数能够较准确地预测缺口试样的拉伸加载过程。由图5可以看出,缺口试样的载荷位移曲线均高于光滑试样,并且随着缺口半径的减小,载荷位移曲线升高。当试样载荷达到峰值时,试样已在强化阶段达到了材料本身的强度极限,随着试样拉伸位移的不断增大,试样的横向尺寸会突然急剧减小,直至断裂。

▲图5 试样载荷位移曲线

缺口试样的屈服强度或抗拉强度随应变的增大而提高,这一现象称为缺口强化。试样拉伸强度应变曲线如图6所示。由图6可知,缺口试样相较于光滑试样,屈服强度和抗拉强度均有所提高,并且随缺口半径的减小,试样的强度提高。当材料所受应力状态不同时,材料内产生的塑性变形与应力集中程度也有所不同,材料的断裂机理会发生变化。为反映材料受力时的复杂应力状态,引入应力三轴度来反映对材料塑性变形能力的约束程度。

▲图6 试样拉伸强度应变曲线

一般认为,应力三轴度反映了应力场中三轴应力状态和对材料变形的约束程度,会直接影响材料的塑性变形及断裂行为。在应力场中,通常用平均应力与等效应力之比来表征应力三轴度的大小,为:

(1)

式中:σ*为应力三轴度;σ1、σ2、σ3为主应力。

试样在进行拉伸试验时无法测出试样的三个主应力,因此无法计算出各试样的应力三轴度,也很难对试样的拉伸强度及断裂失效进行预测。布里奇曼公式为经验公式,将颈缩自由表面看作圆弧,假定周向应变等于径向应变,从而推导出缺口试样最小截面的应力三轴度表达式。笔者采用布里奇曼公式对光滑试样及缺口试样的应力三轴度进行估算,为:

(2)

式中:R为颈缩表面的曲率半径;r为颈缩处横截面的最小半径。

根据布里奇曼公式,计算得出光滑试样及缺口试样的应力三轴度分别为0.33、0.48、0.60、0.82,由此可以对各试样的拉伸强度及断裂失效进行预测。

4.2 缺口尺寸对应力集中程度影响

光滑试样及缺口试样的最小截面应力三轴度云图如图7～图10所示。光滑试样及缺口试样为轴对称结构,由图7～图10可清晰地观察到试样在拉伸过程中的应力集中部位。不同试样的应力三轴度曲线如图11所示。由图11可以看出,试样缺口尺寸不同,试样标距段的应力三轴度有明显差异。试验中,试样的拉伸方式均为单轴拉伸,光滑试样的应力三轴度始终为0.33,半径16 mm、半径8 mm、半径4 mm缺口试样的应力三轴度依次位于0.39～0.76、0.48～0.93、0.60～0.99范围内。结合上文,由布里奇曼公式计算得出的光滑试样及缺口试样应力三轴度也在此范围内,因此笔者所采用的试样本构关系、约束参数及仿真步骤正确可行。

▲图7 光滑试样最小截面应力三轴度云图

▲图8 半径16 mm缺口试样最小截面应力三轴度云图▲图9 半径8 mm缺口试样最小截面应力三轴度云图▲图10 半径4 mm缺口试样最小截面应力三轴度云图▲图11 试样应力三轴度曲线

应力三轴度能够综合反映材料发生塑性变形能力的约束程度,当试样处于受拉状态时,应力三轴度越大,试样的塑性变形能力越弱,反之,试样的塑性变形能力越强。试样的应力三轴度增大时,会相对提高试样的屈服强度及抗拉强度。因此,随着试样缺口半径的减小,试样的应力三轴度位移曲线升高,符合图11的加载趋势。

在拉伸过程中,试样的塑性应变主要集中在颈缩区域,断裂也往往从颈缩区域的中心部位开始,因此分别对光滑试样及缺口试样颈缩处单元进行分析。对于光滑试样,标距段无明显缺口,应力集中现象不明显,并且始终处于单轴拉伸状态,应力三轴度值基本保持不变。对于缺口试样,中心缺口处单元在进入塑性变形后应力三轴度跳跃式增大,随着拉伸位移的增大,应力三轴度平缓减小,此时试样的塑性变形能力提高,缺口处发生肉眼可见的塑性变形。

4.3 缺口尺寸对拉伸强度影响

光滑试样及不同尺寸缺口试样断裂面电镜图片如图12～图15所示。观察时,观测点始终为试样的起裂位置,由此获得不同应力状态下起裂时的机理。光滑试样和缺口试样扫描电镜的观测点位于试样心部,试样起裂的机理均为孔洞正断,此种断裂机理称为韧窝型正断。断裂面的韧窝形貌主要受应力三轴度及塑性应变的影响,其中,韧窝的大小主要受应力三轴度的影响,韧窝的深浅主要受塑性应变的影响。试样在拉伸过程中,拉伸位移增大,直至断裂失效,试样直径最小中心处应力三轴度最大。试样断裂面的应力三轴度越大,试样的塑性变形能力越弱,且应力集中明显,因此断裂面韧窝所占的面积较大。由图12～图15可以明显观察到,随着缺口半径的减小,试样断裂面的韧窝逐渐增大。

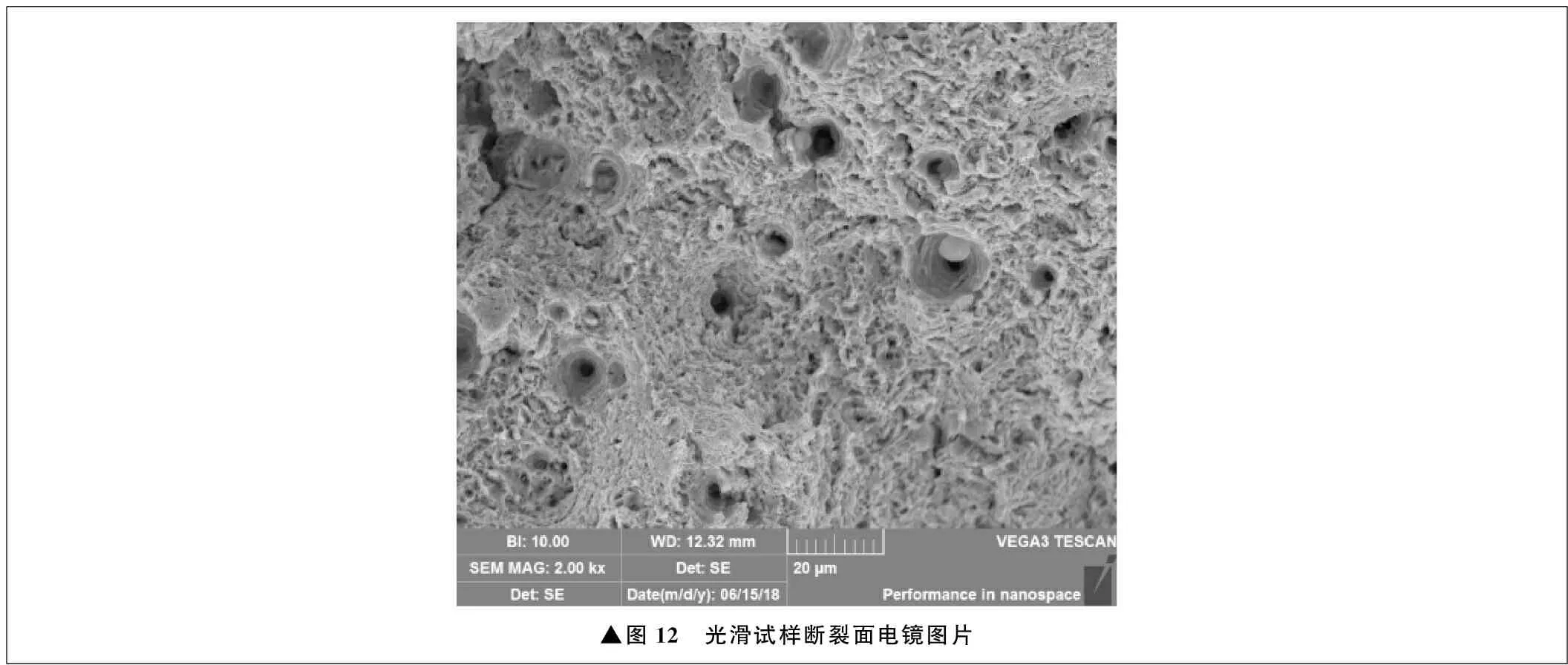
▲图12 光滑试样断裂面电镜图片

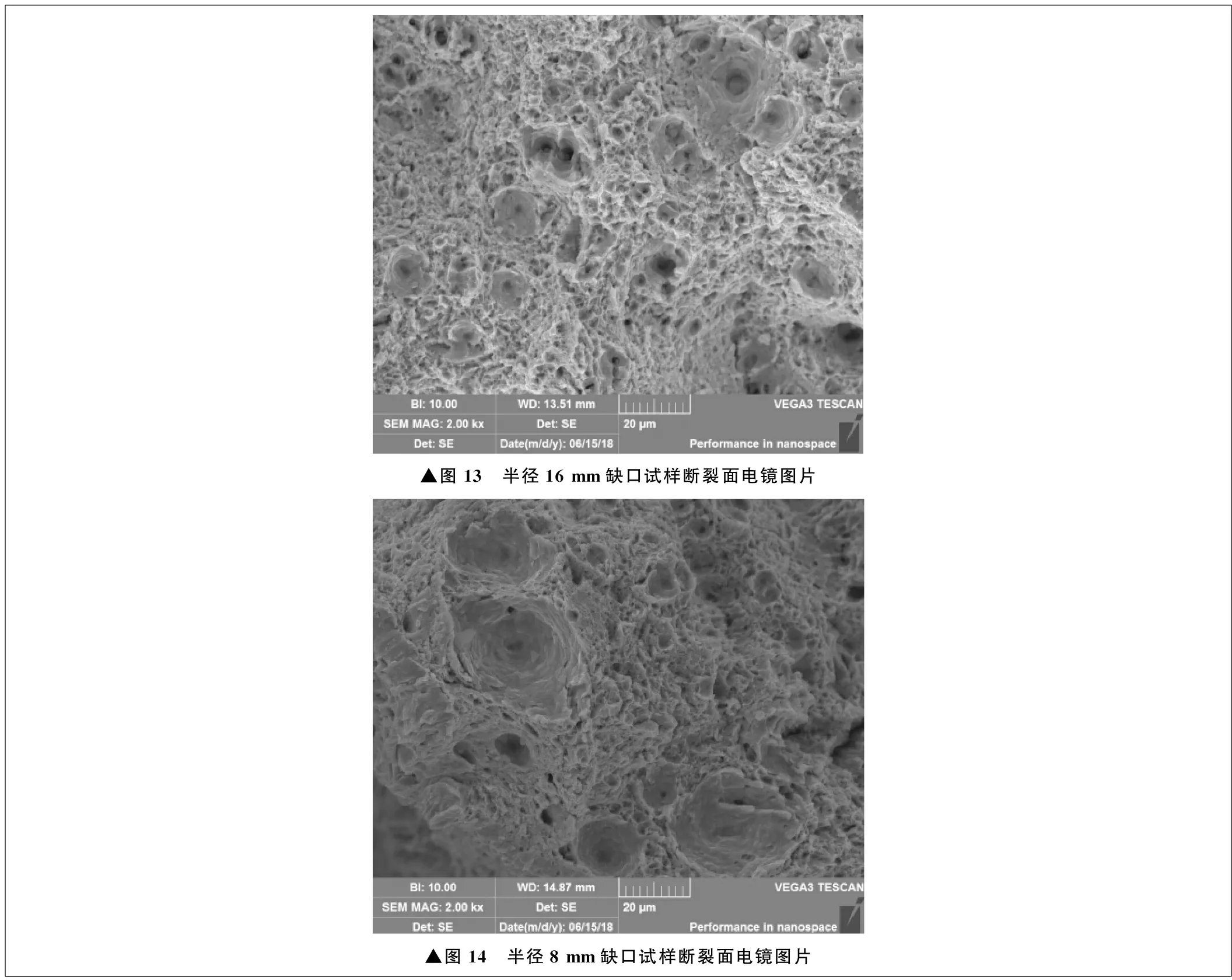
▲图13 半径16 mm缺口试样断裂面电镜图片▲图14 半径8 mm缺口试样断裂面电镜图片

▲图15 半径4 mm缺口试样断裂面电镜图片

5 结论

笔者对光滑试样与不同尺寸缺口试样进行拉伸试验,对试验所得数据进行拟合,验证以光滑试样的本构关系及性能参数为基础对缺口试样拉伸过程进行仿真分析的可行性,并仿真分析得到ML20MnTiB钢不同尺寸缺口试样拉伸过程中的应力三轴度分布。通过对试样断口进行扫描电镜分析,得出三方面结论。

(1) 通过拉伸试验实测所得到的数据,可以拟合得出ML20MnTiB钢的载荷位移曲线。由曲线的拟合程度可知,以光滑试样的本构关系及材料性能参数能够较准确地预测缺口试样的拉伸加载过程。

(2) 试验和仿真分析结果表明,缺口试样相较于光滑试样,屈服强度和抗拉强度均有所提高,并且随着缺口半径的减小,试样的强度提高,即随着应力三轴度增大,试样的失效应力增大。

(3) 由试样断裂面电镜图片可知,各试样断裂机理均为韧窝型正断,随着缺口半径的减小,即随着三轴度的增大,断裂面上的韧窝聚合程度提高,形状逐渐趋于球形,韧窝半径逐渐增大。