变式训练在高中数学解题中的应用

黑龙江省北安市通北林业局第一中学校 贾悦琪

一、变式训练的应用价值

高中数学解题教学中常遇到三种类型题：标准型、探究型和变式型。标准型作为最常见的题目，有固定的答案与解题方法；探究型在高中数学中是比较有难度的，对学生思维能力的要求比较高；变式型是对标准型进行转换而来的，变式训练主要是通过对题目进行转换来解决问题，其解题的过程其实就是学生数学能力提高的过程。

（一）提高学生的学习能力

变式训练以学生的成绩为核心，从问题的不同方向进行分析，用不同的方法对问题进行解答，引领学生参入进来，共同思考、研究，进而培养学生的思维能力。在变式训练中，要让学生了解解题方法的多变性，进一步提高学生的分析能力。在高中数学教学中，应用变式训练不仅能对学生的解题方法进行扩展，还能提高学生的综合能力和自主学习的能力。

（二）增进师生感情

在变式训练中，教师要对学生有充分了解，多从学生的角度考虑问题，做到互相尊重。第一，根据学生发展的需求，对自身的角色进行定位，不仅做教导者，还做学生学习路上的指路明灯，对其进行引导；第二，要与学生建立良好的师生关系，熟悉学生的学习状况，培养学生主动学习的能力，使其感受到学习的乐趣；第三，在教学过程中，要创新教学模式，引导学生大胆提问与探讨；第四，在课堂教学中，要面带笑容，用心爱护每一名学生，建立平等互爱的师生关系，进一步增强师生之间的感情。

（三）培养学生的思维能力

在教学概念、理论和公式时，要通过对公式进行不同程度的转换，引导学生发现其中的相同之处，进而把握其本质，培养思维能力。

二、变式训练的应用方式

（一）一题多变法

一题多变法就是把一道数学题变换成多道数学题。在讲解题目时，教师应对经常出错的典型题目详细讲解，通过不同方式增强学生的分析能力，提升学生的应变能力。

例如，若f（x）=mx2＋8x+4的定义域为R，求实数m的取值范围。

分析：偶次根式若有意义，需保证被开方数非负。解决这道题目较容易，主要利用转化的思想，将该题目转化成恒成立问题求解。

定义域为R,则mx2＋8x+4在R上恒成立。

解：由题意：mx2＋8x+4≥0在R上恒成立。

∴m>0且△≤0，得m≥4，

∴m的取值范围是[4，+∞）。

变式：f（x）=log3（mx2＋8x+4）的值域为R，求实数m的取值范围。

分析：令t=mx2＋8x+4，若要使f（x）的值域为R，则t可以取到全体正实数。

解：令t=mx2＋8x+4，则要求t可以取到全体正实数。

①当m=0时，t能取到所有正实数，

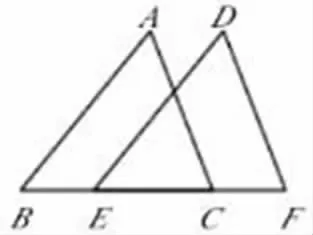
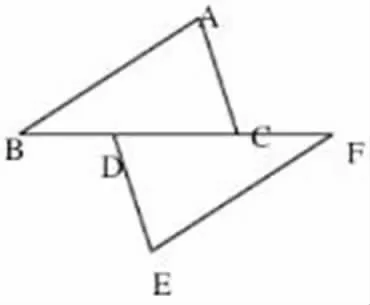
②当m≠0时，m>0且△≥0，则0

∴0＜m＜4。

综上可得：m的取值范围是[0,4]。

这个变式把函数的定义域、取值范围和相关题型进行融合，有助于学生进一步了解知识之间的关系，也有助于学生复习巩固基础知识，增强学生的学习自信。

在解答高中数学题时，通常都有多种方法，很多题中都包含多个知识点，注重考查学生在日常学习中对相关知识点的掌握情况。教师要引导学生进行一题多变转换，进一步提高学生的分析能力和解题水平，促进学生数学成绩的提升。高中生的学习任务重，内容多，若对题目进行分类总结，对常错题进行变式训练，将会大大缓解教师的教学压力，提升课堂教学效率。

（二）一题多解法

一题多解法是进行变式训练的另一种方法。在课堂教学中，教师要引导学生在已知条件的基础上分析题目，但不要局限于已知条件，要调动学生的创新性思维，进一步提高学生的解题能力。

例如，解不等式3<2x-3<5。

解法一：根据绝对值的定义，进行分类讨论求解。

（1）当2x-3≥0时，不等式可化为3＜2x-3＜5，则3＜x＜4。

（2）当2x-3＜0时，不等式可化为3＜-2x+3＜5，则1＜x＜0。

综上：解集为3

解法二：转化为不等式组求解。

原不等式等价于|2x-3|＞3且|2x-3|＜5，

则3＜x＜4或1＜x＜0，

综上：解集为3

解法三：利用等价命题法。

原不等式等价于3＜2x-3＜5或-5＜2x-3＜-3，

即3＜x＜4或-1＜x＜0，

综上，解集为3

在上述题目中，解法一根据绝对值的相关知识，通过分类讨论进行解答，这就要求学生较好地掌握与绝对值相关的基础知识。解法二根据不等式组的转换解答问题，主要考查学生对不等式的掌握情况。解法三采用的是等价命题法，相当于将原不等式进行等价转化，主要考查学生对原不等式进行等价转化的能力。一题多解实际上就是对问题进行不同角度的分析，不但可以增加学生的知识储备，还可以培养学生的创造思维能力，进一步增强学生的综合素质。

（三）多题归一法

高中数学知识覆盖面广，内容多，虽然每次考试都会涉及很多知识点，但考查重点一直都是对所学知识的实际应用能力。所以在平时的教学中，教师要注重引导学生运用多题归一法解题。

例如：如图1，点B、E、C、F在一条直线上，AB=DE,AC=DF,BE=CF。

图1 例题

求证：∠A=∠D。

评析：本题主要训练学生运用“边边边”条件判定三角形全等，进而运用全等三角形的性质得出所求证的角相等。由条件BE=CF不难得出BC=EF，又有已知条件AB=DE，AC=DF，利用“边边边”条件可得△ABC≌△DEF，从而∠A=∠D得证。这就是一道简单的变式训练题。

可以结合此题命制以下几道题：

变式一：如图2，已知AC=EF，BC=DE，点A、D、B、F在一条直线上，要使△ABC≌△FDE，还需添加一个条件，这个条件可以是_________。

图2 变式一

评析：本题采用的是与上题同样的方法，通过添加条件证明两个三角形全等，并运用“边角边”理论进行三角形全等的验证以及运用三角形的性质对其夹角进行相等的论证。由条件AC=EF，BC=DE，且点A、D、B、F在一条直线上，得知∠A=∠F，进而通过“边角边”得知，添加的条件是∠A=∠F，促使△ABC≌△FDE。

变式二：如图3，点B、D、C、F在一条直线上，且BC=FD，AB=EF。请你只添加一个条件（不再加辅助线），使△ABC≌△EFD，你添加的条件是_______。

图3 变式二

评析：变式二同样也是应用“边角边”理论对三角形全等进行验证，由已知条件点B、D、C、F在一条直线上，且BC=FD,AB=EF，可以得出∠B=∠F，由此可知添加的条件是∠B=∠F，进而可以证明△ABC≌△EFD。

这两道变式题都应用了三角形的相关理论，都是对多题归一法的综合运用。多题归一法就是运用固定的基础知识，通过不同的方式对不同问题进行转换，如转换条件、转换结论、转换图形等。在课堂教学中，教师要鼓励学生运用多题归一法，以此训练学生的创造性思维。大多数学题虽然题型不同，但问题的本质都一样，应引导学生对其进行深入分析，总结题目的规律，掌握答题的技巧，提高应变能力。

综上所述，要提高学生的思维能力，就要在高中数学教学中融入变式训练，以此帮助学生更好地掌握解题思路，提升解题能力，进而提高课堂教学效率。