航班时刻初级市场配置优化模型研究进展
2022-12-27冯慧琳王德芸张军峰
冯慧琳,胡 荣,王德芸,张军峰
(南京航空航天大学,民航学院,南京 211106)
0 引 言
近年来民航运输业蓬勃发展,2010—2019 年全球(国际民航组织缔约国)定期航班运输总周转量的年复合增长率为6.28%,而在此期间我国运输总周转量的复合增长率更是高达10.23%。2019年我国机场年起降架次突破1 166 万,快速增长的航空业务需求与有限资源之间的矛盾日益突出,导致机场日益拥挤,航班正常率难以保障,大面积航班延误时有发生。截至2021 年冬春航季,全球协调机场共170 座,其中我国航班时刻主协调机场有22 座,这些机场的业务需求远超其容量,时刻资源非常紧张,往往会出现比较严重的延误现象。
为缓解供求不平衡,增加容量和管理需求是两种常见的方法。通过扩建机场、开放空域以提升机场容量和终端空域通行能力,是缓解机场拥挤、提高航班正常率的有效手段。然而,此类方法需要投入大量资金并且建设周期长,短期内无法解决机场的时刻资源紧缺问题[1-2]。此外,部分拥挤机场受物理空间、噪声限制等约束无法通过新建跑道来提升容量。因此,需求管理是短期内缓解延误的有效手段,而航班时刻优化配置是需求管理的重要手段[3]。
2020 年开始,受新冠肺炎疫情的影响,航空运输量有所下降,拥挤机场的延误有所缓解。但随着疫苗的普及,各国陆续开放边境,航空业务量正稳步恢复。2021 年我国机场完成飞机起降978 万架次,已恢复至2019年的84%。我国《“十四五”民用航空发展规划》中指出:2023—2025 年是增长期和释放期,重点要扩大国内市场、恢复国际市场。2025年预计保障起降1 700万架次,达到2019年的146%,2035 年预计保障起降3 000 万架次,是2019年的2.57 倍。从长远来看,我国作为人口最多的发展中国家,民航运输市场需求潜力巨大,起降架次与航班时刻需求将刚性增长。如何进一步优化航班时刻配置、改进运营管理模式,成为实现稀缺资源供需平衡、推动民航高质量发展的重要议题之一。
1 航班时刻配置概述
国际航空运输协会(International Air Transport Association,IATA)发布的《世界机场航班时刻准则》(Worldwide Airport Slot Guidelines,WASG)中将航班时刻定义为:由协调员给予的计划运营许可,凭此在特定日期和时间在三级机场使用进场或离场所需的一切机场基础设施。我国对航班时刻的定义与IATA 类似,具体指航空器在指定日期和时间,为抵离某个机场而使用相关基础设施与服务的权利,且强调航班时刻的时间是基于挡轮挡时间和撤轮挡时间。
航班时刻配置可分为初级市场配置和次级市场配置。航班时刻初级市场配置是指航班时刻管理部门完成历史航班时刻确认和调整,并将航班时刻池(所有可供配置的航班时刻的集合)中的时刻分配给航空承运人。航班时刻管理部门首先应完成历史时刻确认和调整工作,未确认为历史时刻的,进入时刻池进行配置。在时刻配置集中办公前,航班时刻管理部门应公布时刻池,并接受航空承运人的时刻申请;在集中办公期间,航班时刻管理部门和航空承运人对航班时刻配置结果予以现场确认;在集中办公后,航班时刻管理部门会同飞行计划管理部门对航班时刻进行编排。
初级市场配置完成后,已经配置给航空承运人的时刻进入航班时刻库。部分航空承运人可能未获得理想时刻,可对时刻库中的时刻开展交换、转让、租赁、买卖和共同经营等多种方式的航班时刻次级市场配置活动,以满足其时刻需求。航班时刻配置的简要流程如图1所示。其中,航班时刻管理部门是指负责航班时刻配置管理的机构或部门。在我国,航班时刻管理部门指中国民用航空局和各民航地区管理局。
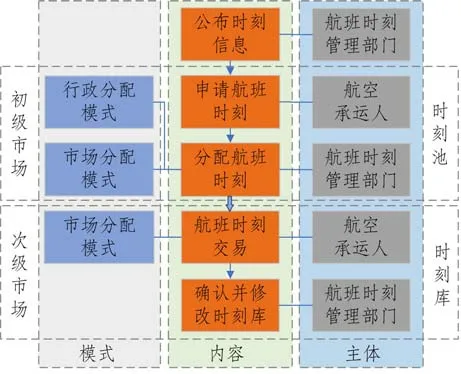
图1 航班时刻配置流程Fig.1 Slot allocation processes
航班时刻配置模式一般分为三种:行政分配模式、市场分配模式和混合分配模式[4],但混合分配模式本质上是将行政和市场分配模式相结合。因此,基础的时刻配置模式实质上只有两种:行政分配模式和市场分配模式。行政分配模式是应用最广泛的模式,即航班时刻管理部门按照制定的时刻管理规则分配时刻,而不考虑航空承运人的支付意愿[5-6]。在这种模式下,管理部门按照规定的优先顺序对时刻进行分配,“祖父权利”和“非用即失”原则是其主要特点[7]。然而,多项研究表明,行政分配由时刻管理部门主导,不考虑时刻对航空承运人的价值,因此分配效率往往较低,且容易产生抑制市场竞争、时刻滥用等不良影响[8-9]。Zografos 等[10]指出即使在拥挤机场,也有超过10%的已分配时刻没有被使用。且由于时刻资源稀缺、新增时刻有限,新进入的航空承运人往往很难通过行政分配在拥挤机场获得时刻[11-12]。因此,一些研究提出引入市场分配模式,以提高时刻利用效率。
市场分配模式是以市场为基础,以价格、税费等经济杠杆手段实现时刻资源分配。在航班时刻初级市场和次级市场均可实施[13]。初级市场的市场化配置一般通过时刻拍卖、拥挤收费等方式来实现[14-16];次级市场的市场化配置主要包括时刻交换、转让、租赁、买卖、共同经营等形式[17-19]。但如果任由市场对航班时刻进行支配,极易导致财力雄厚的航空承运人通过大量购买时刻,进而占据市场主导地位,造成市场垄断[20-21]。且航空承运人通过市场交易所获时刻,相比于行政分配无偿获得的时刻,成本必定上升,航空承运人可能会推高票价将成本转嫁给消费者[13,22]。事实上,目前还没有国家完全通过市场化方式来分配航班时刻[23],常见的时刻配置方式如表1所示。
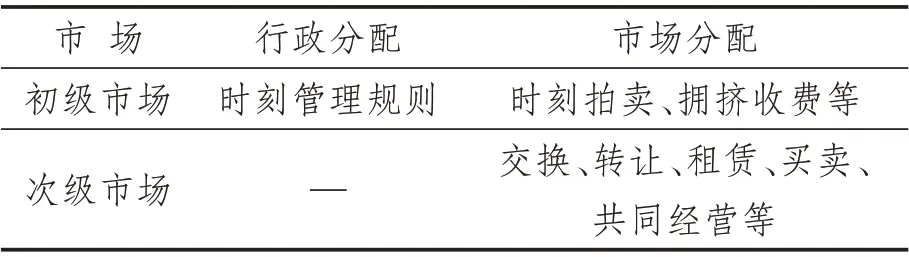
表1 时刻配置的主要方式Tab.1 Main techniques for slot allocation
因而,部分国家探索采用混合分配模式,美国、欧洲和中国的航班时刻配置政策如表2 所示。美国初级市场新增的航班时刻采用抽签进行分配,在次级市场允许航班时刻进行交换、买卖和租赁,但不同机场对具体交易方式有进一步规定[24]。美国曾在拉瓜迪亚机场(四字码:KLGA)、约翰·肯尼迪机场(KJFK)和纽瓦克机场(KEWR)的航班时刻初级市场配置中尝试引入拍卖机制,然而,美国政府问责办公室裁定联邦航空局(Federal Aviation Administration,FAA)无权进行拍卖,拍卖方案最终被取消[13]。

表2 时刻配置政策的典型案例Tab.2 Typical cases of slot allocation regulations
欧盟和英国在航班时刻初级市场完全采用行政分配模式;在次级市场积极探索航班时刻的市场化分配方式,允许航班时刻在航空承运人之间有条件地开展时刻交换、时刻转让及共同经营。然而,货币化交易仅在英国的希思罗机场(EGLL)和盖特威克机场(EGKK)较为活跃[16,23]。
我国在2018 年印发的《民航航班时刻管理办法》中,明确了我国航班时刻配置的具体规则,即:初级市场航班时刻实行行政化配置,次级市场航班时刻实行市场化配置。同时,民航局近年也开展了初级市场航班时刻的市场化配置改革试点:在广州白云机场开展“时刻拍卖”的试点;在上海浦东机场开展“时刻抽签+使用费”的尝试。这些试点工作旨在引入市场机制,发挥组合优势,提高航班时刻配置效率。
尽管很多国家允许开展航班时刻次级市场配置活动,但市场并不活跃,时刻交易量不大[25]。航班时刻初级市场配置,尤其是基于行政分配的初级市场配置仍是时刻配置的主要方式。以我国民航业为例,全国运输机场2035 年的目标保障起降3 000 万架次,是2019 年的2.57 倍,未来新增航班时刻量非常大,而新增时刻主要通过初级市场进行配置。由此可见,航班时刻初级市场配置占据基础性、主体性地位,而次级市场配置则是对初级市场配置的有益补充与完善。因此,本文将重点从基于行政分配与基于市场分配两个视角梳理航班时刻初级市场配置优化模型的研究进展。
2 基于行政分配的初级市场配置
2.1 优化目标
基于行政分配的航班时刻初级市场配置的优化目标主要分为两类:分配的效率性和公平性。效率性目标追求总体时刻分配最优,而公平性目标则强调时刻配置更为公正、平等。
2.1.1 效率性
基于行政分配的效率指标主要从两方面考虑:一是针对已配置的航班时刻,从时刻调整量(航班申请时刻和分配时刻之间存在的差异,即航班时刻需求提报表和航班时刻计划表的差异)的角度设置,例如最小化时刻调整总量;二是针对因容量等限制而未配置的时刻设置相应指标。例如,一些研究[26-27]指出时刻优化配置的首要目标应是最小化未分配时刻申请的数量,尽量使所有的时刻申请都能得到分配。
Zografos 等[6]率先以时刻调整总量最小为目标,建立航班时刻行政分配的整数规划模型。在此基础上,很多文章改进该目标,提出累计时刻调整量、加权时刻调整量、时刻平方调整量等指标。为防止部分时刻的调整量过大,一些文章又提出以最小化最大时刻调整量、最小化超过可接受调整量的时刻数量为优化目标,如图2所示。
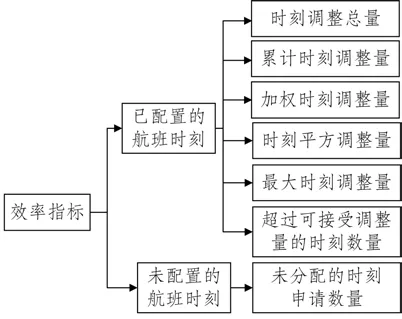
图2 时刻行政分配的效率指标Fig.2 Efficiency indices of administrative slot allocation
(1)最小化时刻调整总量
时刻调整总量指所有航班时刻申请的调整量之和。很多文章[27-29]以最小化时刻调整总量为目标,如式(1)所示:
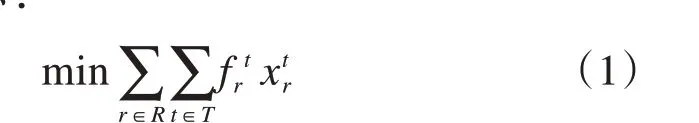

(2)最小化累计时刻调整量
航班时刻调整总量计算的是时刻申请的调整量,但因每个时刻申请所对应的执行天数不同,故不能准确反映时刻配置偏差[30]。因此,可采用累计时刻调整量作为优化目标[30-32],即用时刻的调整量乘以其执行天数,得到一个时刻系列的调整量之和,如式(2)所示:

(3)最小化加权时刻调整量
时刻调整总量和累计时刻调整量默认每个航班时刻的价值是相同的。然而,对航空承运人来说,每个航班的价值往往是不同的,和机票票价、载客数、运行时间等诸多因素相关。因此,Jacquillat 和Vaze[33]提出如下最小化加权时刻调整量的优化目标:式中:δr为航班r的价值。
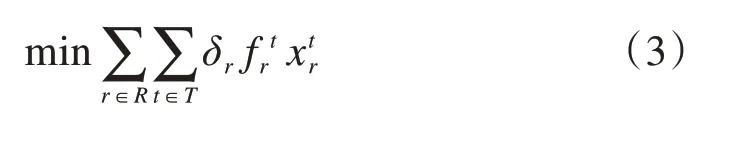
(4)最小化时刻平方调整量
时刻平方调整量是对时刻调整量进行平方处理,目的是对较大的时刻调整量进行惩罚,使时刻调整量的分布更加均匀[32]。计算如式(4)所示:
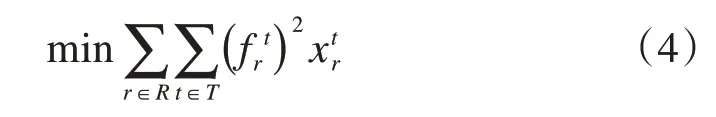
(5)最小化最大时刻调整量
仅从时刻调整量的总和上加以约束,可以达到总体效率最优。然而,可能导致部分时刻的调整量过大。因此,部分研究[27,29,33]在上述优化目标的基础上引入最小化“最大时刻调整量”构建优化模型,如式(5)所示:
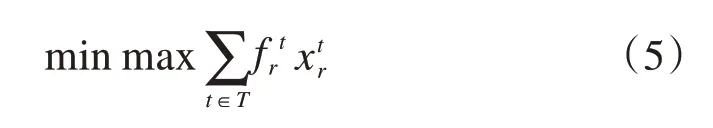
(6)最小化超过可接受调整量的时刻数量
每个时刻都有可接受的调整区间,而不能无限制地将其提前或推后。因此,在优化目标设置中可考虑最小化超过可接受调整量的时刻数量[28,34],如式(6)所示:

(7)最小化未分配的时刻申请数量
部分时刻申请,可能由于容量约束、过站时间限制等原因无法得到分配。因此,一些文章[26-27]认为时刻优化配置的首要目标是最小化未分配的时刻申请数量,如式(7)所示:

式中:η为时刻申请总数;yr是二值变量,如果航班r被分配了时刻,yr=1,否则yr=0。
各优化目标的特点和优劣性如表3 所示。现有研究成果中,既有选取单个上述指标设置优化目标,也有选取多个指标设置多目标优化模型,且多目标优化模型受到越来越多的关注。

表3 优化目标的特点和优劣性Tab.3 Characteristics,advantages,and disadvantages of optimization goals
2.1.2 公平性
前文提到的最大时刻调整量、时刻平方调整量、超过可接受调整量的时刻数量等指标从一定程度上体现了公平性的思想,但无法衡量时刻配置的公平程度。公平性成为继效率性之后航班时刻优化目标设置的另一个重要考量。
公平性包括横向公平性和纵向公平性[35]。横向公平性指有相同属性和条件的群体应享受相当的权利、承担相当的义务。纵向公平性有两层含义:一是指具有不同属性和条件的群体的效益应与其付出相匹配;二是指对于弱势群体应给予帮助,以满足其基本需求。显然,航班时刻配置优化问题既要考虑横向公平性,也要兼顾纵向公平性。
横向公平性在时刻配置中的具体体现是时刻申请属性相同(如时刻申请数量相同或申请的高峰时刻数量相同)的航空承运人应分配到相同的时刻数量和时刻调整量。纵向公平性的第一个方面体现在分配给航空承运人的时刻数量和时刻调整量应与其时刻申请相匹配;纵向公平性的第二个方面体现在对弱势方的帮助,如我国对国家基本航空服务时刻、使用国产飞机运行的航班优先配置,以满足基本需求。大部分航班时刻配置模型研究中的公平性指标从时刻调整量的角度出发,涵盖横向公平性和纵向公平性的第一个方面。然而,目前尚未有文章将纵向公平性的第二个方面融入公平性指标,未来可从此方向进一步扩展、深化航班时刻配置的公平性评价。
从公平性视角出发,航空承运人的时刻调整量应与其时刻申请数相匹配。基于此,Zografos和Jiang[36]提出如式(8)所示的航班时刻配置的公平性度量方式。航空承运人的公平性评价指标为其时刻调整量占比除以其时刻申请数占比,表征实际时刻调整量与应分配的时刻调整量的比例:
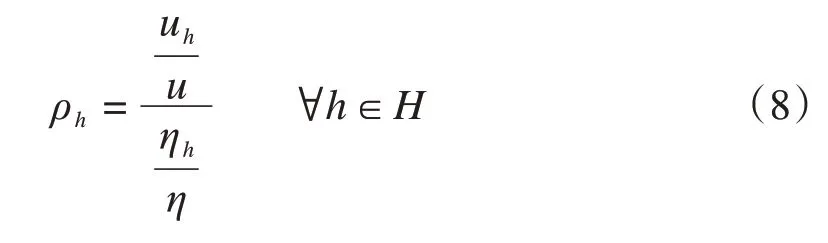
式中:H为所有航空承运人的集合;h为某一航空承运人;ρh为航空承运人h的公平性评价指标;u为所有时刻申请的调整总量;uh为航空承运人h的所有时刻申请的调整量之和;ηh为航空承运人h申请的时刻数量。
显然,如果航空承运人h受到绝对公平的对待,ρh= 1;如果0 ≤ρh<1,说明航空承运人h实际的时刻调整量小于应分配的时刻调整量,对其有利;如果ρh>1,说明航空承运人h实际的时刻调整量大于应分配的时刻调整量,对其不利。
因此,可以将ρh与1 比较,构建绝对公平目标函数,从而避免分配结果出现极端不公平的现象。绝对公平目标函数为最小化受到最差待遇的航空承运人的公平值与绝对公平值的偏差,如式(9)所示:
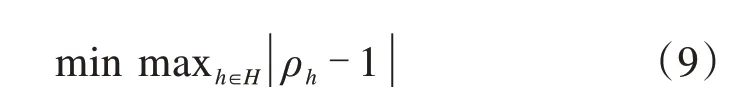
Jiang 和Zografos[37]还采用相对公平目标和基尼系数来评价时刻配置的公平性。
相对公平目标反映了航空承运人的公平性值与所有航空承运人的平均公平性值的差异,差值越大,说明该航空承运人受到越不平等的对待,如式(10)所示[37]:
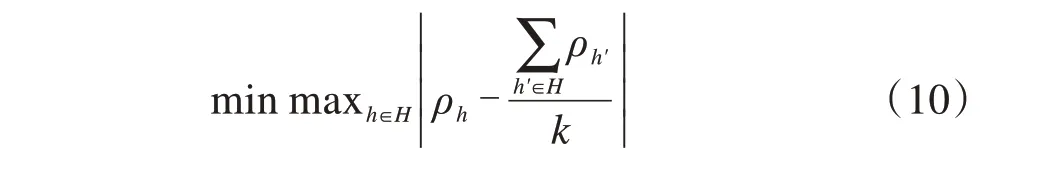
式中:k为航空承运人的数量。
基尼系数从整体上反应时刻配置的公平性,但不能衡量特定的航空承运人在时刻配置中受到公平对待的程度。航班时刻配置的基尼系数如式(11)所示[37]:
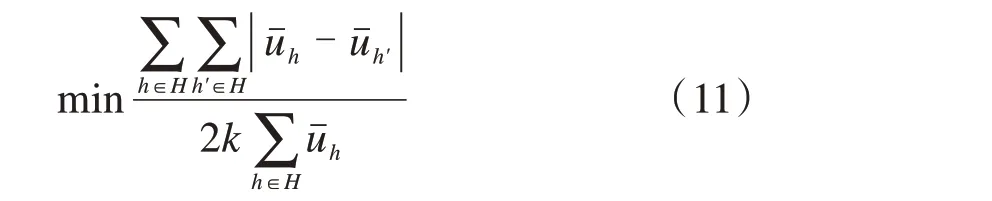
式中:uˉh为航空承运人h所有时刻申请的平均调整量。基尼系数的取值范围为[0,1],基尼系数越小意味着时刻调整量的分配越平均;若基尼系数为0,表示每个航空承运人的平均调整量相等,时刻配置完全平均。
上述方法对所有时刻申请一视同仁,但在实际运行时,高峰时段的时刻申请较多,容易超过机场容量,表现出供不应求;而非高峰时段的时刻申请数量往往低于容量,呈现供大于求的情形。因此,如果将高峰时刻和非高峰时刻同等的对待,实际上间接地惩罚了非高峰时刻的申请。因此,航空承运人的时刻调整量应与其高峰时段的时刻申请数相匹配。基于此,Fairbrother 等[38]和Katsigiannis 等[39]提出基于需求的公平性指标(式(12)),要求分配给某个航空承运人时刻调整量的占比大约等于其在高峰时段提出的时刻申请占所有高峰时段的时刻申请数的比例:
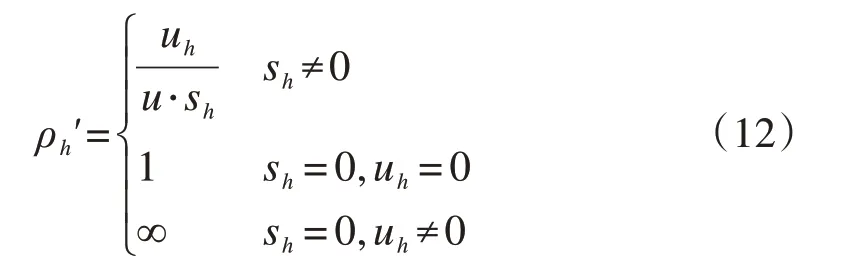
式中:sh为航空承运人h高峰时刻的申请数量占高峰时段的时刻申请总数的比例。
若ρh'=1,表示航空承运人h受到公平的对待;若0≤ρh'<1,表示航空承运人h受到优待;若ρh'>1,表示航空承运人h受到不公平对待。
Jacquillat 和Vaze[33]根据航班的价值,对时刻调整量进行加权,将航空承运人h各航班时刻调整量的加权平均值作为公平性评价指标,如式(13)所示:式中:Rh为航空承运人h的时刻申请集合。如果绝对公平,各航空承运人公平性指标ρh''的数值应相等,即任一航空承运人航班时刻的加权调整量与其时刻申请数量成正比。
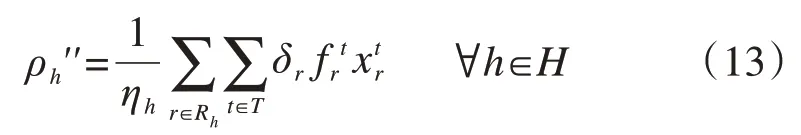
然而,Jacquillat 和Vaze 并未给出计算航班价值的方法。航班的价值受到航班属性(客运/货运,国内/国际,短途/长途)、机型、运行时间等诸多因素的影响,因而,精确地评估航班价值较为复杂。目前还未有精确计算航班价值并融入到航班时刻配置模型中的研究,未来可深入研究这一方向。
公平性指标拓展了航班时刻优化目标的研究内涵,已成为优化目标选取的重要考量因素。
2.2 约束条件
航班时刻行政分配属于整数规划问题,通常包括3 个基础性约束条件:唯一性约束、容量约束和过站时间约束[6]。当然,根据研究的具体内容与实际需求,可以补充考虑其他约束条件,如图3所示。
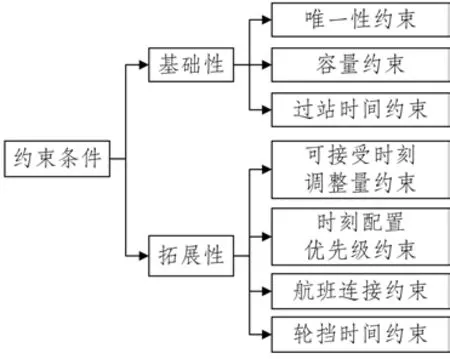
图3 航班时刻行政分配的约束条件Fig.3 Constraints on administrative slot allocation
2.2.1 唯一性约束
唯一性约束指每个航班只能分配一个时刻,所有的研究文献都包含这一约束条件,如式(14)所示:

2.2.2 容量约束
大多数研究仅对跑道容量进行约束,规定起降需求不能超过跑道滚动进场容量、离场容量和总容量[34,39],如式(15)~(17)所示:

式中:α、β是容量包络曲线的参数;C是跑道容量。
此外,一些研究不仅考虑了跑道容量约束,还考虑了机场其他基础设施和空域的容量限制。诸如:Zeng 等[40]考虑停机位容量和走廊口通行能力约束,吴慎之等[41]考虑进离航路点容量约束,Katsigiannis 和Zografos[27]考虑跑道、停机位、航站楼容量约束的时间差异,等等。
2.2.3 过站时间约束
过站时间约束通常划分为不过夜航班(离场时刻和进场时刻在同一天)和过夜航班(离场时刻在进场时刻的后一天)两种情况。
一些研究仅从最小过站时间的角度,对前后紧邻航班的过站时间进行约束[6,32,37],如式(19)、(20)所示。式(19)表示不过夜航班的最小过站时间约束,式(20)表示过夜航班的最小过站时间约束:


2.2.4 可接受时刻调整量约束
一些研究从时刻可接受调整量的角度考虑,定义超过可接受调整量的时刻数量,如式(23)~(27)所示[28,34]:
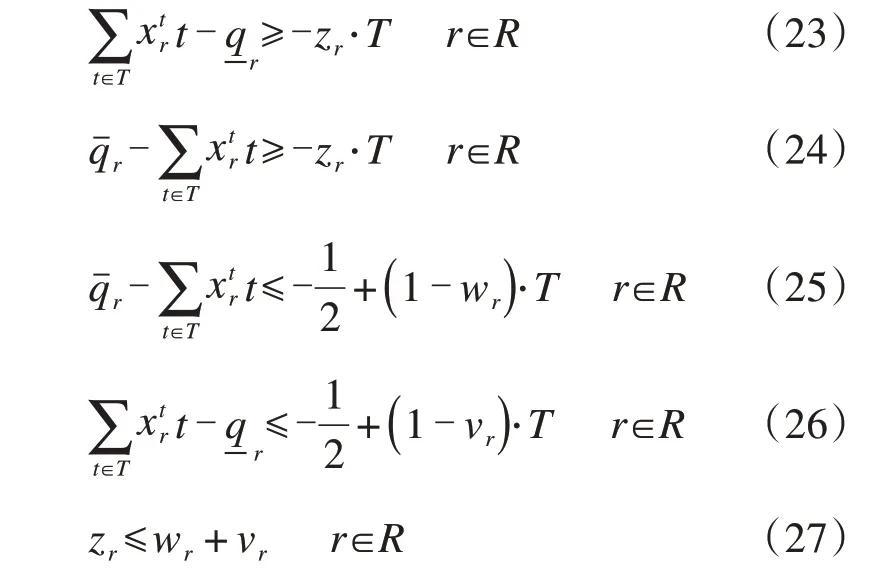
式中:wr是二值变量,如果航班r被分配到的时刻晚于qˉr,wr= 1,否则wr= 0;vr是二值变量,如果航班r被分配到的时刻早于-qr,vr= 1,否则vr= 0。
式(23)、(24)定义了zr,统计了分配给航班r的时刻超过其可接受时刻调整量的情况,航班可接受时刻的区间为[-qr,qˉr]。如果分配的时刻早于下限-qr或晚于上限qˉr,zr= 1,否则zr= 0;式(25)、(26)分别定义了wr和vr,统计了分配给航班r的时刻未超过其可接受时刻调整量的情况;式(27)表示如果wr和vr中有一个为1,则zr= 1。
此外,Androutsopoulos 和Madas[30]考虑到航空承运人在特定机场的市场势力,赋予每个航空承运人一个时刻调整权重,分配给航空承运人的时刻调整量的占比应约等于该权重,从而使时刻配置较为公平。时刻调整权重是根据航空承运人对机场拥挤的贡献度,即航空承运人的时刻申请导致其他航空承运人时刻调整的程度来确定的。
2.2.5 时刻配置优先级约束
WASG 规定航班时刻初级市场配置的优先顺序为:历史航班时刻确认、历史航班时刻调整、新进入航空承运人协调配置以及其他时刻协调配置。因此,一些文章在构建时刻配置模型时,考虑到不同优先级时刻的配置顺序,将总模型分解为4个子模型依次进行求解,得到更符合WASG 要求的时刻配置结果[27,31,42]。
2.2.6 航班连接约束
机场网络的航班时刻配置,需要考虑出发地和目的地的时刻匹配。每个航班的出发地和目的地的时刻要么都得到分配,要么都没有分配,如式(28)所示[26,42]:
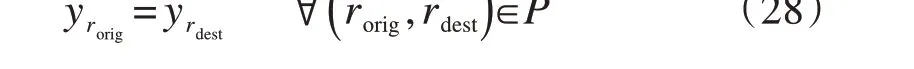
式中:P为航班时刻对集合,包括航班出发时刻和航班到达时刻;rorigrdest分别为航班出发/到达时刻申请;yrorigyrdest是二值变量,如果航班被分配了出发/到达时刻,则yrorig/yrdest= 1,否则yrorig/yrdest= 0。
2.2.7 轮挡时间约束
机场网络的时刻配置,需要用轮挡时间将各机场的航班时刻关联起来。在对多机场进行时刻配置时,为简化考虑,通常认为航班飞行时间是固定的,如式(29)所示[29,42]:

2.3 基于不确定容量的时刻配置
上述研究仅考虑战略分配阶段(得到航班时刻计划)的时刻配置,且采用固定容量约束(多为机场公布容量)。然而,在实际运行中,战略阶段的时刻配置和战术阶段的时隙分配(得到航班实际运行时隙)是相关联的。此外,机场容量容易受到天气等不确定因素的影响,并非一个定值。因此,机场公布容量和实时容量可能存在较大差异,用固定容量约束航班时刻配置可能导致实际运行时发生大规模的延误。因此,一些研究考虑容量的不确定性,将战略分配阶段和战术分配阶段相结合,构建两阶段时刻配置模型。
在传统的容量固定的模型中,只考虑战略分配阶段的时刻配置,且通过公布容量限定时刻配置的上限。而在基于不确定容量的时刻配置模型中,考虑到战略分配阶段机场容量是未知的,而实际运行时(即战术分配阶段的特定情景下)容量是已知的。因此,在战术分配阶段构建多种容量情景,并求出每种情景下的延误成本,结合每种情景发生的概率得到期望延误成本。战略分配阶段的优化目标在原先时刻调整量的基础上,增加最小化期望延误成本的目标,以权衡时刻调整和运行延误。
Corolli 等[43]首先提出一个两阶段的多个机场的时刻分配模型,优化目标为最小化时刻调整总量和期望延误成本的加权和。根据每个机场的历史天气情况,设定不同情景,对应不同的机场容量,从而求出延误的航班数量,并由此得到延误成本。在考虑延误成本时,文章考虑到机场内航班延误的传播。以5个欧洲机场为例,模型相较于容量固定的模型可以减少286.4%的延误成本,目标函数值的提升比例为14.2%。Wang 和Zhao[44]提出了一个机场网络时刻分配的鲁棒模型,通过减少最坏情况下的潜在拥挤来表征鲁棒性。根据机场公布的容量,设定了20个容量减少的情景,通过计划偏差成本(未分配时刻的成本、时刻调整的成本)和运行拥挤成本(超过容量的航班数量)之间的权衡,将时刻配置的战略阶段和战术阶段联系起来,并选取深圳宝安(ZGSZ)、广州白云(ZGGG)、三亚凤凰(ZJSY)三个主协调机场为算例,考虑容量不确定性的模型相较容量固定的模型,目标函数值提升的比例最高可达47.5%。
然而,上述文章中的延误成本仅根据延误的航班数量确定,而未考虑具体的延误时间,限制了模型的实用性。亓尧等[45]从航班延误时间的角度计算延误成本,假设容量服从线性不确定分布,分别构建了单个机场和多个机场的两阶段时刻配置模型。以京津冀、长三角和珠三角机场群为算例,验证了两阶段模型相较于传统的容量固定模型可以有效减少运行延误,目标函数值提升比例均超过10%,最大提升比例达到了71.3%(珠三角)。大部分文章在研究多个机场时刻配置时,为简化考虑,认为航班飞行时间是固定的。Wang和Jacquillat[46]在战术阶段的时隙分配时,将飞行时间限定在一个范围内,用目视或仪表运行代表天气条件,设定不同的容量情景,提出两阶段的机场网络航班时刻配置模型,第一阶段的模型如式(32)~(36)所示:

式(32)表示时刻配置的目标为最小化时刻调整总量和期望延误成本的加权和;式(33)是唯一性约束,表示每个航班只能分配一个时刻;式(34)表示在战略分配阶段,假定航班飞行时间是固定的;式(35)表示最小过站时间约束;式(36)表示决策变量是二值变量。
第二阶段是时隙战术分配阶段,如式(37)~(48)所示。时刻战略分配和时隙战术分配阶段的差别主要在于,战略分配阶段分配的航班计划时刻可以比航空承运人申请的时刻提前或推后,而战术分配阶段分配的实际起飞时隙只能晚于计划起飞时刻。式(37)表示对于每一情景ω,优化目标为最小化该情景下的延误成本;式(38)是唯一性约束,表示每个航班只能分配一个时刻;式(39)和(40)分别定义了出发和到达的延误时间,实际起飞时隙只能晚于计划起飞时刻,而实际到达时隙由于飞行时间的机动性,可以早于计划到达时刻;式(41)、(42)表示航班出发和到达的延误时间不能超过最大允许的延误时间;式(43)表示最小过站时间约束;式(44)、(45)表示飞行时间在一定范围内;式(46)表示特定情景下的容量约束;式(47)表示决策变量是二值变量;式(48)表示延误时间为正。具体如下所示:
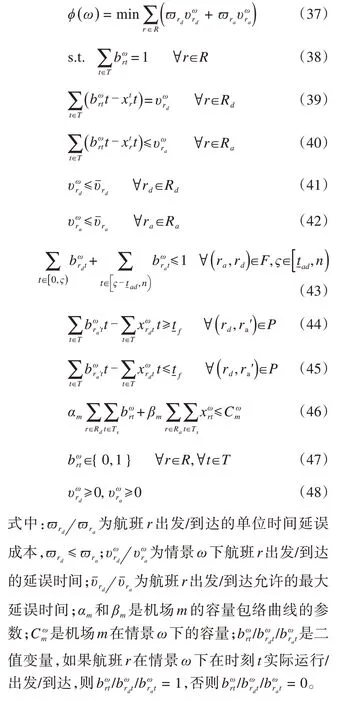
3 基于市场分配的初级市场配置
航班时刻初级市场配置的市场化探索主要包括时刻拍卖和拥挤收费。时刻拍卖是指通过航空承运人的投标竞价,将时刻分配给最重视它的竞拍人。拥挤收费则是通过对高峰时刻起降的航班收取拥挤费用,迫使一部分航班从高峰时刻转移至非高峰时刻。
3.1 时刻拍卖
航班时刻拍卖旨在通过市场价格机制,将航班时刻分配给对其估价最高的航班时刻承运人。对时刻估价高的航空承运人更倾向于充分利用该时刻,因此时刻拍卖能有效减少时刻滥用[16]。由于时刻对航空承运人而言并非相互独立,航班到达时刻和出发时刻需要相互匹配。因此,时刻拍卖应采用组合拍卖的形式[47],将相互关联的时刻(例如航班的出发时刻和到达时刻)捆绑成时刻组合进行拍卖,航空承运人如果中标,则获得时刻组合中的所有时刻。
航班时刻组合拍卖根据拍卖周期数可以分为一次性拍卖和迭代拍卖[48]。一次性拍卖只有一个交易周期,竞拍人需一次性提供所有组合的报价;迭代拍卖由多个交易周期组成,竞拍人可以多次提交投标,并根据交易中所获得的信息,更改报价,直至达到设定的拍卖结束条件。
一些研究建议采用一次性密封拍卖的方式拍卖初级市场时刻。Rassenti等[47]率先提出在航班时刻初级市场开展一次性密封组合拍卖,以修正行政分配不恰当的时刻。航空承运人可以将航班的出发时刻和到达时刻捆绑成一个时刻组合进行投标,从而防止只获得航线的部分时刻。Pertuiset 和Santos[49]基于Vickrey-Clarke-Groves(VCG)密封拍卖机制提出一种欧洲拥挤机场的初级市场时刻拍卖系统,以确保分配效率、激励相容、灵活和透明性。将一天划分为不同的时段,高峰时刻每1小时分为一个时段,非高峰时刻每2 小时分为一个时段,具体如式(49)~(52)所示:

VCG 拍卖最大的优势是竞拍人的占优策略是以其对时刻的估价作为投标价格,而不用考虑其他竞拍人对时刻的估价。但是,VCG 拍卖容易鼓励竞拍人私下串通[50]。
此外,Ball 等[51]考虑到在不同延误水平下,航空承运人对时刻的估价不同,定义了不确定数量的时刻拍卖(Quantity-Contingent Auctions,QCAs)模型,根据竞拍人提供的信息确定时刻的总销售数量。每个航空承运人不仅需要提供时刻组合和报价,还需指定该报价下可接受的每个时间窗口的时刻数量,即提供特定延误水平下对时刻组合的报价。同时引入市场份额限制,分别分析了低、中、高单位延误成本情境下不确定数量的拍卖对社会福利的影响。
一次性密封组合拍卖虽然在一个交易周期内就可以完成,然而,由于竞拍人在拍卖前要列出所有可能的时刻组合以及适当的投标价格,这些要求对竞拍人比较苛刻。此外,一次性密封组合拍卖是对时刻组合报价,而无法获得航空承运人对每个时刻的估价。为解决这些问题,包含多个交易周期的迭代拍卖形式应运而生。时钟拍卖就是一种较常见的航班时刻迭代拍卖形式。时钟拍卖一般分为两个阶段:第一个阶段航空承运人根据拍卖人宣布的价格指定他们想要购买时刻的数量,如果需求超过容量,拍卖人会提高价格,航空承运人根据新的价格重新指定购买时刻的数量,整个过程循环往复,直到任意时间段内的时刻需求都低于容量或前后两轮拍卖收入的增加低于阈值;第二个阶段投标人根据第一个阶段获得的信息,递交最终的投标,拍卖人以此确定赢家。Ball等[16]建议采用时钟拍卖的方式对时刻进行拍卖,并指出给予永久性使用权的时刻拍卖不能提高时刻的利用效率,而有使用时间限制的拍卖会使时刻定期重新分配,有利于创造充满活力的竞争环境。Ball 等[52]、Sheng 等[53]和Araúzo 等[54]也建议采用向上叫价时钟拍卖的方式进行航班时刻初级市场拍卖。然而,Levin 和Skrzypacz[55]指出需谨慎设计拍卖机制,否则竞拍人很可能在时钟拍卖的第一阶段释放虚假信息以误导其他竞拍人。
3.2 拥挤收费
拥挤收费指对特定机场特定时间起降的航班收取费用,增加航班在高峰时刻的运营成本,从而将运行效率较低的航班转移至非高峰时刻运行,减少高峰时刻的航班量。发生延误时,航空承运人只能感知到自身的延误成本,而忽略了给其他航空承运人带来的额外成本,形成外部不经济。外部不经济等于社会边际成本与私人边际成本之差,如图4 所示。拥挤收费能有效弥补外部不经济,实现社会效益最大[56]。在未收取拥挤费用的情况下,航空承运人会选择私人边际成本曲线与需求曲线的交点A 对应的流量,而社会最优的流量是社会边际成本曲线与需求曲线的交点B对应的流量。拥挤收费的目的是通过收取(P2-P3)的费用,使得航空承运人选择社会最优流量L2。
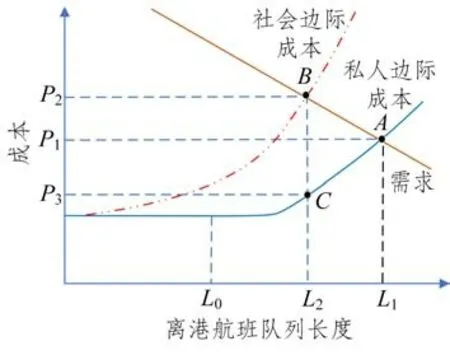
图4 拥挤收费示意图[57]Fig.4 Schematic of congestion pricing
Levine[58]率先提出应设计一种类似于道路拥挤收费的方式,基于航空器对机场拥挤的贡献程度征收拥挤费,来替代现有的基于航空器重量收取起降费的做法。然而,机场的拥挤收费和道路不同。道路用户是相互独立的,而航空承运人所占的市场份额不同,部分外部拥挤成本可能已经内化到航班成本中,故航空承运人之间并非相互独立[56]。但是,Daniel[59]指出拥挤成本内化可以忽略不计,并基于随机瓶颈模型,考虑随机队列、时变交通流率、内生性交通调整,计算均衡拥挤收费价格。通过对明尼阿波利斯-圣保罗机场(KMSP)的仿真模拟,证明拥挤收费能有效调整航班时刻。此后,Daniel[60]将模型进一步拓展,将航空承运人细分为商业航空、支线航空和通用航空,考虑需求弹性、运行时间偏好和成本的异质性,发现拥挤收费将增加大型商业航空承运人、旅客和机场的收益,减少支线航空和通用航空承运人的收益,且增加量大于减少量。
Brueckner[61]指出当航空承运人在机场处于完全垄断地位时,拥挤成本完全内化,故在完全垄断市场中拥挤收费不起作用。Pels 和Verhoef[62]同样认为需要考虑拥挤成本内化,指出基于边际延误成本收取拥挤费并非最优策略,并建立了一个考虑寡头竞争、延误成本内化和机场之间的政策协调的、以社会福利最大化为目标的模型。研究认为拥挤收费的下界应设置为0,且不同机场之间的合作可能是不稳定的,但不合作可能导致福利低于不收拥挤费的情况。Czerny 和Zhang[63]将旅客划分为商务旅客和休闲旅客,商务旅客的时间价值更高。文章指出不同旅客类型对机场拥挤收费有重大影响,可以提高机场收费和机票价格,以保护商务旅客免受过度拥挤。他们进一步考虑对商务旅客和休闲旅客收取不同的票价,建立一个两阶段博弈模型:第一阶段以最大化福利(消费者剩余、航空承运人和机场的利润之和)为目标确定机场收费,第二阶段航空承运人在商务和休闲旅客的数量上进行竞争,发现最优机场收费的基本结构与航空承运人是否采取价格歧视无关[64]。Hu 等[57]建立了一个包括航空承运人成本、旅客延误成本和环境成本的拥挤定价模型,以计算不同时间和队长的拥挤收费。王琨等[65]考虑机场和航空承运人两方利益,将航班划分为直达航班和联程中转航班,建立双层规划模型。上层模型如式(53)~(55)所示,决策者为机场管理方,优化目标为机场收益最大,包括经济收益和延误减少带来的社会效益:


式(53)为目标函数,机场收益等于拥挤收费和航班正常起降收益之和减去延误成本;式(54)为拥挤收费费率范围的限制;式(55)表示拥挤收费应小于预期增量收益。
下层模型的决策者为航空承运人,目标为航班广义时间消耗最小,如式(56)、(57)所示:
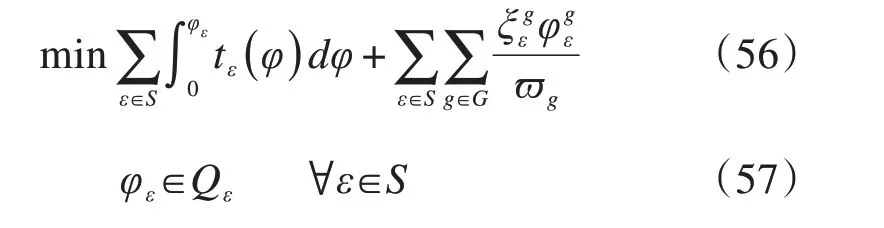
式中:φε为时段ε上的航班量,为所有类型航班量之和;Qε为时段ε上航班量的可行域,上限为时段ε的容量,下限为0。
式(56)表示优化目标为机场内航班广义时间消耗最小,包括实际时间消耗和费用消耗转化的时间消耗;式(57)表示容量约束。
拥挤收费没有严格的容量约束,而是通过收费的方式,使运行效率较低的航班转移至非高峰时刻运行。拥挤收费增加了航班调整的灵活性,能有效提高航班时刻的利用率。然而,拥挤收费定价在实际操作中较为复杂,需要考虑市场模式、拥挤成本的不确定性、航空承运人的不同偏好、交通需求弹性等诸多因素。因此,拥挤收费的研究目前还停留在理论阶段,尚未得到实际运用。
拥挤收费不限制单个时刻航班配置数量的上限,而是通过对外部成本收费的方式,实现航班运行的削峰填谷;而时刻拍卖的时刻数量是根据机场容量和行政分配的时刻数量确定的。一些研究比较了不同市场模式和目标下的时刻拍卖和拥挤收费的有效性。时刻拍卖和拥挤收费各有利弊,如表4所示。

表4 时刻拍卖和拥挤收费比较Tab.4 Comparisons between slot auction and congestion pricing
此外,拥挤收费和时刻拍卖理论上可以同时实施,例如,对新增时刻进行拍卖,同时对高峰时刻运行的航班收取拥挤费。然而,尚未有研究将两种市场分配方式结合考虑。未来可设计一种结合拥挤收费和时刻拍卖的市场分配机制,分析两种方式的相互影响,并与单一的市场分配方式进行比较,探讨该市场机制的特点。
4 未来研究展望
4.1 行政分配模型研究展望
基于行政分配的初级市场配置模型的研究较为完善,能较好地模拟航班时刻配置的实际情况,但仍有如下内容值得深入研究:
(1)研究对象的拓展。大部分文章基于WASG的时刻配置规则,构建单目标或多目标的单个机场时刻配置模型。近几年不少文章考虑到机场网络中出发时刻和到达时刻的相互依赖,构建了多个机场的时刻配置模型。从单个机场拓展到多个机场再拓展到机场群和机场网络,主要增加了航班连接约束、飞行时间约束。然而,大部分文章将飞行时间设定为定值,而未考虑其机动性与不确定性。除航班连接约束、飞行时间约束外,机场群内的机场存在共用航路点,但鲜有研究考虑共用航路点的容量约束。此外,机场群的时刻配置模型求解较为复杂,如何改进算法,快速计算出最优配置结果,值得进一步研究。
(2)时刻配置优先级的调整。一些文章根据WASG 规定,将时刻按照历史航班时刻确认、历史航班时刻调整、新进入航空承运人协调配置以及其他时刻协调配置赋予不同的时刻配置优先级。但在操作中,一些特殊情况的时刻申请往往会给予优先考虑。例如,我国国家基本航空服务和使用国产飞机的航班,在时刻申请时会优先考虑。因而对于新增的航班时刻,采用何种优先级进行分配,以及如何将这种顺序在优化模型中体现,都值得深入研究。
(3)效率性优化目标的深化。行政分配的优化目标主要从效率和公平两个角度考虑,追求航班时刻调整量的总体最优和均衡分配。在效率性指标方面,现有研究大部分从航班时刻调整量的角度考虑,而很少考虑到时刻调整的成本。未来可考虑引入航班时刻价值,进而计算出时刻调整的成本。航班时刻价值受到诸多因素影响,如航班时刻、月份、航班属性、执飞机型,等等,如何计算航班时刻价值并将其融入到时刻配置中,值得深入研究。同时,时刻配置时应考虑航空承运人的历史时刻利用情况。对于航班执行率高、正点率高的,应优先考虑。此外,可以考虑时刻配置对环境承载力和旅客满意度的影响。
(4)公平性优化目标的深化。现有研究更多从航空承运人的角度考虑公平性,追求时刻调整量在航空承运人之间的公平分配,涉及横向公平性和纵向公平性的第一个方面。然而,对于纵向公平性的第二个方面,即对于弱势方应给予帮助(例如,我国对国家基本航空服务时刻、使用国产飞机运行的航班优先配置),尚未有文章将此类考虑融入公平性指标,未来可从此方面进一步扩展公平性评价。此外,鲜有文章从机场的角度考虑公平性。机场群中的机场存在共用进离场航路点,需合理分配航班通过进离场航路点的时刻,避免冲突[68]。因此,可以分析机场在时刻配置中的公平性,并兼顾机场的功能定位。
(5)容量的协同约束。大部分文章仅考虑跑道容量约束(如进场/离场/总滚动容量)。然而,航站楼、停机位、空域及环境等容量也会对时刻配置产生影响。如何构建全过程的容量约束,并考虑时间的差异性,值得深入研究。
(6)时刻配置的不确定性。考虑不确定性是航班时刻配置模型构建的一个重要方向。近几年一些研究从容量不确定性的角度,构建了综合战略分配和战术分配阶段的时刻配置模型。大部分研究根据天气条件对各机场容量的影响,设置容量情景,但没有考虑到机场群中机场容量的相关性。如果机场地理距离较近,受到的天气影响可能相似,对容量的影响也可能相似。同时,跑道运行模式、航空器到达顺序、航空器起降间隔等因素也会对机场容量产生影响,但鲜有研究考虑这些因素。虽然部分研究在计算延误成本时考虑了机场内航班延误的传播,但没有考虑延误在机场间的传播。此外,容量的不确定性仅是时刻配置过程面临的一类不确定性,其他方面的不确定性(如航线网络的不确定性)还未有文章开展研究。
4.2 市场分配模型研究展望
有关航班时刻初级市场的时刻拍卖和拥挤收费研究,未来可从如下角度进一步拓展:
(1)时刻拍卖机制的设计。现有研究提出的航班时刻拍卖机制主要有两种:一次性密封组合拍卖和时钟拍卖。两种组合拍卖机制各有利弊,如何在此基础上改进或提出一种新的拍卖机制,为竞拍人提供便利,同时避免竞拍人私下串通,值得深入研究。在拍卖机制设计时,应明确时刻报价规则、赢家确定程序、交易费用标准等问题。
(2)时刻拍卖机制的评价。现有文章提出了适用于航班时刻拍卖的机制,如密封组合拍卖、时钟拍卖等,但未针对市场的特点,定量比较不同的拍卖机制。未来可开展时刻拍卖机制的多维评价,并针对我国实际情况针对性地提出实施建议。
(3)拥挤收费的公平性。目前对航班时刻拥挤收费的研究主要以总体效率最高为目标,很少从公平性的角度进行评价,可能导致市场份额低的航空承运人需要比市场份额高的航空承运人支付更多的费用,对中小型航空承运人的发展不利。未来可考虑设置指标进行公平性测度,设计兼顾效率与公平的拥挤收费方案。
(4)拥挤收费的实施研究。拥挤收费的概念提出已有一段时间,但尚未实施。如何选择拥挤收费的对象、确定拥挤收费的起点、获得公众的支持以及拥挤收费收入如何再分配等问题,都关系到拥挤收费方案的可执行程度。因此,未来可分析拥挤收费实施中可能遇到的障碍,并针对性地提出对策建议,推动机场拥挤收费从理论走向实践。
(5)时刻拍卖和拥挤收费的比较和结合。一些文章比较了时刻拍卖和拥挤收费这两种基于市场分配的初级市场配置方式,但大部分是定性研究或将市场简化为完全竞争或假设时刻需求是完全弹性的。未来可开展不同市场模式下的两种配置方式的比较与改进研究。此外,现有研究均是分别研究时刻拍卖和拥挤收费的方法设计、实施影响等,尚未有研究融合两种方式的优点、设计出将两种方式结合起来的市场分配机制。未来可分析两种市场分配方式的相互影响,设计出新的市场分配机制,并与单一的市场分配方式比较,分析市场新机制的优劣势。
5 结束语
虽然疫情对民航运输业造成较大的冲击,但从长期看民航运输业仍处在快速发展的阶段,机场时刻资源日益紧张,亟须优化时刻配置,提高航班的运行效率。本文概述了航班时刻配置模式的特点和实施现状,对初级市场配置优化模型进行了梳理总结,主要结论如下:
(1)航班时刻配置的基本模式包括行政分配和市场分配模式。行政分配模式被各国广泛采用,但容易造成时刻滥用。市场分配模式在初级市场主要包括时刻拍卖和拥挤收费两种方式,但可能带来市场垄断、机票价格上涨等不良影响。欧洲、美国和中国等国家正积极探索行政和市场相结合的混合分配模式。
(2)基于行政分配的初级市场配置模型的研究较为完善,往往基于WASG 分配原则,优化时刻配置效率。一些文章引入公平性指标,兼顾时刻配置的效率和公平。为保证分配的有效性,从唯一性、容量、过站时间、轮挡时间等方面进行约束。未来可以通过拓展研究对象,引入新的优化目标(如环境成本、旅客满意度等)和约束条件(如多系统组合容量、时刻配置顺序等),并考虑时刻配置的多源不确定性,进一步优化模型。
(3)基于市场分配的初级市场配置主要有时刻拍卖和拥挤收费两种方式。时刻拍卖应采用组合拍卖的形式,现有研究认为密封组合拍卖或向上叫价的时钟拍卖是比较合适的拍卖形式,但鲜有文章对这两种形式进行综合评价和比较。拥挤收费通过对外部成本收费的方式,优化时刻配置,实现航班运行的削峰填谷,未来可引入公平性目标,并从拥挤收费实施的障碍和对策的角度进一步深化分析。此外,如何融合时刻拍卖和拥挤收费的各自优势,设计与评价航班时刻市场分配新机制亦值得深入探讨。
