响应用户有限理性需求的微电网优化策略

2022-12-27许志荣张高瑞

综合智慧能源 2022年11期

许志荣，张高瑞

（1.华润电力投资有限公司，广东深圳 518000；2.华润电力（广东）销售有限公司，广州 510640；3.华能澜沧江水电股份有限公司，昆明 650214；4.三峡大学电气与新能源学院，湖北宜昌 443002）

0 引言

微电网作为一种集“分布式电源-负荷-储能”于一体的小型电力系统，为社会能源转型提供了一种有效的解决方案［1］。根据用户用电决策有限理性的特点，用户需求响应时除了考虑自身用电成本，其用电舒适度也是需要考虑的重要因素［2］。微电网系统在处理多目标优化问题时，其优化模型中变量多、复杂度高、求解难度大，很难得到系统最优运行状态。因此选择合适的求解方法，以协调微电网运行成本以及用户用电舒适度之间的关系，是微电网需要解决的一个重要问题。

需求响应是指可以灵活调节自身用电时段以及时长的用户参与微电网系统优化的行为［3-5］。文献［6］针对含热电负荷的多能源微电网系统，建立了基于补偿机制的需求响应模型，实现了多种能源的联合需求。文献［7］提出了一种分层需求响应方案，该方案提高了电网的经济效益。文献［8］在研究分布式电源容量优化时考虑了负荷灵活性，实现了微电网系统运行成本最低的目的。然而上述文献将用户用电决策当作完全理性决策，用户需求响应时仅仅考虑了用户用电的经济性。实际生活中用户的用电决策往往是有限理性决策而非完全理性决策，用电舒适度也将影响用户的用电决策［9］。在考虑用户用电决策为有限理性的研究中，文献［10］提出了一种主从博弈模型，该模型实现了用户、服务商以及网络运营商共赢的局面。文献［11］提出了一种考虑用户选择行为有限理性的电力需求响应机制，实现售电公司和用户双赢的目的。然而上述文献在考虑用户用电决策有限理性时仅考虑了用户的用电成本和微电网的运行成本，并未考虑用户用电舒适度对用电决策的影响［12］。

响应用户用电的有限理性需求，以微电网运行成本以及用电舒适度作为优化目标属于微电网多目标优化问题。在微电网多目标问题上，文献［13-14］针对微电网中系统利润以及系统调度偏差的多目标优化问题，提出一种双层多目标鲁棒优化方法。文献［15］为了提高微电网可再生能源消纳能力，提出了一种基于源荷互补的微电网双层优化方法。然而上述双层优化方法求解过程中上下两层优化目标之间需要来回传输大量的信息，增大了系统优化的复杂度。与此同时，本文有限理性优化函数以及微电网运行成本函数之间因量纲不同无法直接对比分析，且两者优化关系模糊无法同时得到最优解。

基于以上分析，本文在灵活性用电决策有限理性的情况下，建立了考虑用电转移量以及用电转移跨度的用户用电决策有限理性优化模型。该模型在用户需求响应时能够同时兼顾用户的用电成本以及用户的用电舒适度。此外，在优化目标求解上，本文提出了一种具备全局优化能力的GOJaya（Global Optimization Jaya）算法，该算法在迭代前期引入非线性权重因子增加了算法的求解速度，在迭代后期引入单纯形变换提高了算法的求解精度。通过IEEE-33 节点测试系统搭建的微电网模型进行算例分析，验证了本文所提优化策略的有效性和优越性以及GOJaya 算法在求解速度和精度方面的优越性。

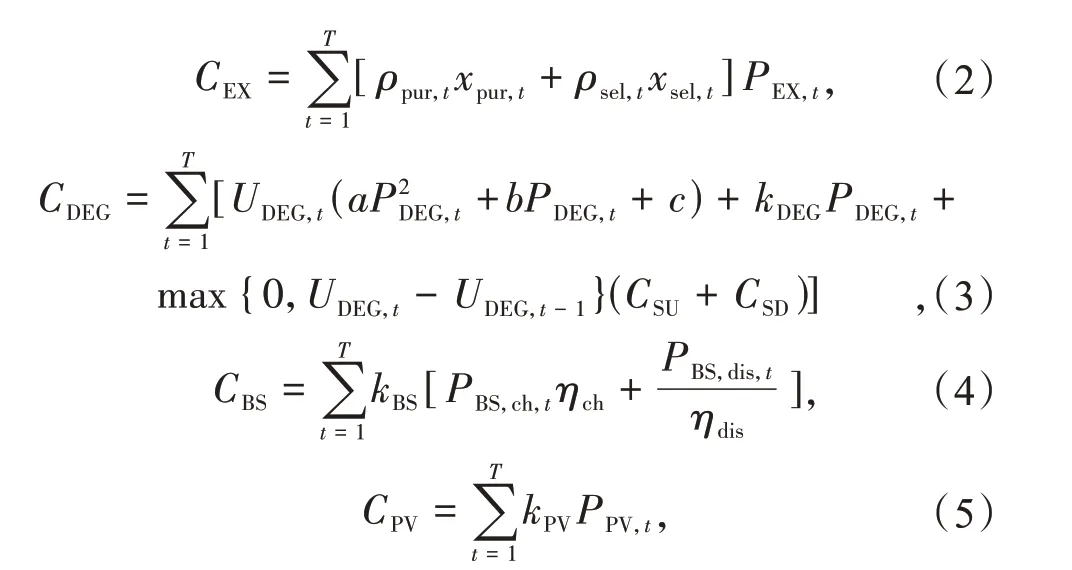
1 微电网多目标优化

微电网结构如图1 所示。图中MGCC 为微电网中央控制器。微电网中的每一部分均与微电网控制中心相连，控制中心收到各设备的信息及配电网相关电价格信息后，统一调度微电网内部各设备出力以满足用户用电需求。

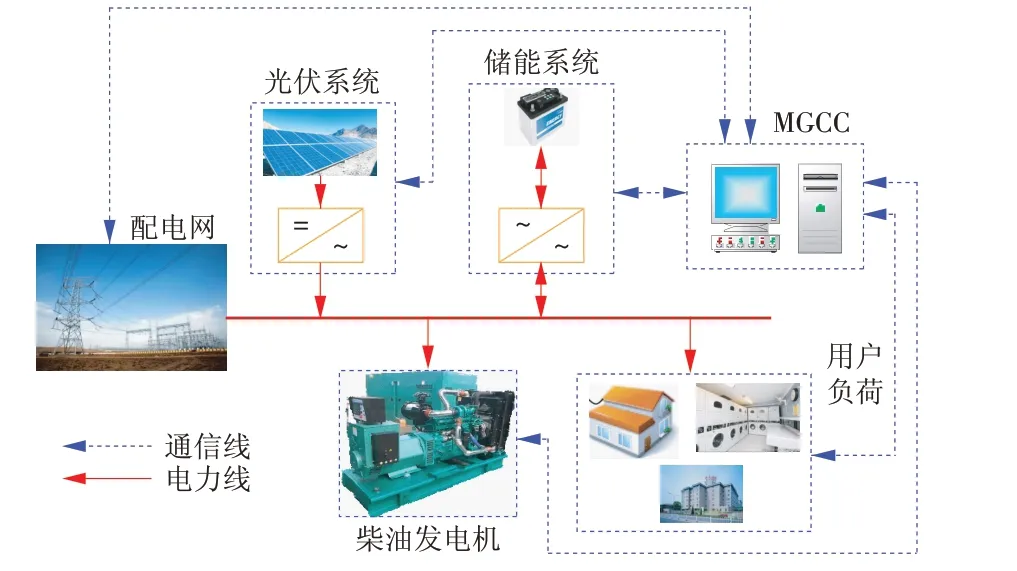
图1 微电网结构示意Fig.1 Structure of the microgrid

1.1 微电网运行成本优化目标

微电网运行成本为

式中：CEX为微电网购售电成本；CDEG为柴油机发电运行维护成本；CBS为储能电池维护成本；CPV为光伏运行维护成本；t为单位优化时间；T为总调度周期时间；xpur，t，xsel，t分别为购、售电状态变量；ρpur，t，ρsel，t分别为购、售电价格；PEX，t为购、售电功率；a，b，c为燃料成本系数；PDEG，t为柴油机的输出功率；UDEG，t为柴油发电机的状态变量，取0 或1；kDEG为柴油机的维护系数；CSU，CSD分别表示柴油机启停成本系数；kBS为蓄电池的维护成本系数；PBS，ch，t，PBS，dis，t分别为蓄电池的充、放电功率；ηch，ηdis分别为蓄电池的充、放电效率；kPV为光伏运行成本系数；PPV，t为光伏输出功率。

1.2 微电网运行成本函数约束条件

微电网运行成本函数约束主要包括联络线功率平衡约束、分布式电源出力约束、蓄电池荷电状态约束。具体为

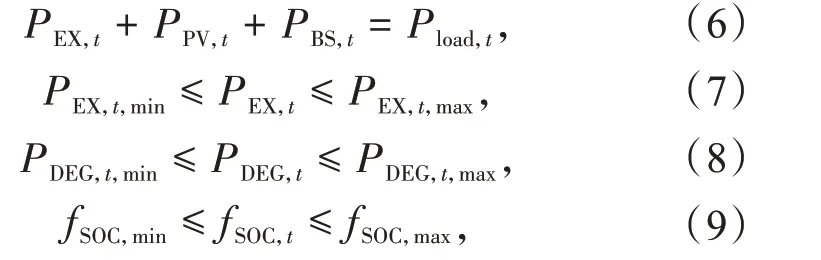
式中：Pload，t为用户用电功率；PBS，t为蓄电池功率；PEX，t，min，PEX，t，max分别为最小、最大购、售电功率；PDEG，t，min，PDEG，t，max分别为柴油机最小、最大输出功率；fSOC，min，fSOC，max分别为蓄电池最小、最大荷电状态。

1.3 用户用电决策有限理性优化模型

根据行为经济学理论，现实中用户的用电决策具有有限理性，用户需求响应时不能仅仅考虑用电成本的问题。本文根据用电习惯将用户分为4 类：第1 类为重要用户，第2 类为可平移用户，第3 类为可转移用户，第4 类为可削减用户。其中2，3，4 类用户统称为灵活性用户并参与需求响应。参与需求响应后，用户的用电舒适度将会降低。为了用户需求响应时兼顾用户的用电舒适度，本文以衡量用电舒适度标准的用户用电转移量比S1以及用户用电转移跨度比S2作为用户有限理性决策的优化目标［16］，即

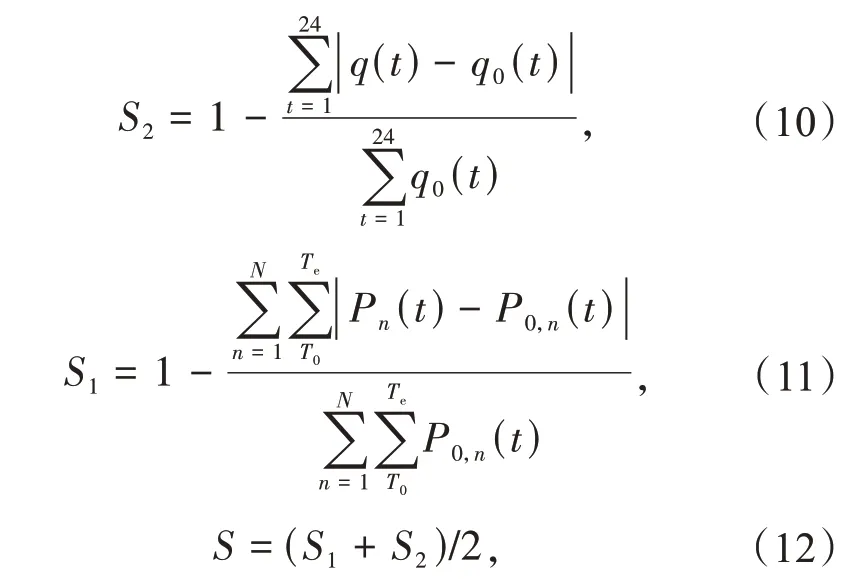
式中：q0(t)为灵活性用户响应前用电量；q(t)为灵活性用户实际用电量；P0，n(t)为灵活性用户n需求响应前功率；Pn(t)为灵活性用户n需求响应后功率；T0为需求响应前时间；Te为需求响应后时间；N为参与需求响应用户的总个数；S为用户有限理性优化函数，并将S作为微电网另一个优化目标，令f2=S。

1.4 微电网多目标优化问题单目标化

微电网运行成本函数及有限理性优化函数之间存在量纲不同以及优化关系模糊的问题。为了解决此问题，本文采用降半Γ 形隶属度函数对微电网各优化目标进行归一化处理，将微电网多目标优化问题转化为单目标优化问题。微电网运行成本隶属度函数μ1及有限理性优化函数μ2为

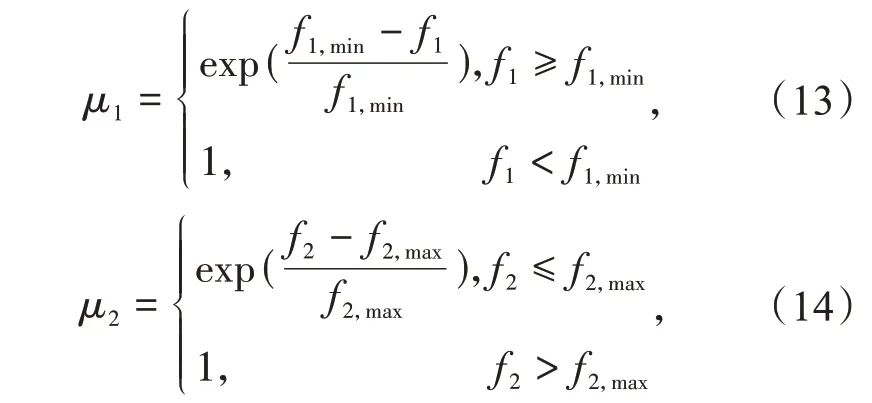
式中：f1，min为微电网运行成本最小值；f2，max为用户用电有限理性优化函数最大值。

定义指标f为微电网系统总优化目标为

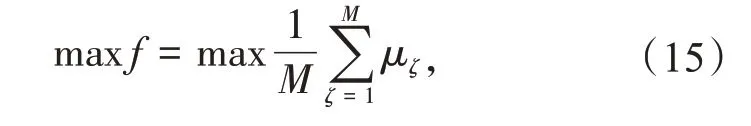
式中：M为子优化目标个数；ζ为子优化目标编号。

微电网系统新增约束条件为

2 微电网优化模型求解方法

本文在Jaya 算法基础上提出了一种全局优化Jaya 算法GOJaya，以求解前文所提的微电网优化目标。GOJaya 算法在Jaya 算法中引入了非线性递减权重因子以及单纯形变换，以解决Jaya 算法求解过程中存在的求解速度慢以及精度低的问题。

2.1 GOJaya算法的非线性递减权重因子

Jaya 算法在迭代过程中算法的搜索范围、速度以及精度由随机值r1，k，i，r2，k，i决定［17-18］。在Jaya 算法迭代前期，当r1，k，i和r2，k，i差值较小时，候选解X'j，k，i改变幅度较小，候选解对于当前最优解Xj，k，i继承程度较大。本文在GOJaya 算法中引入一个非线性递减权重因子ω以平衡r1，k，i和r2，k，i对算法迭代前期搜索速度以及搜索范围的影响。候选解公式更新为

2.2 GOJaya算法的单纯形变换

在算法迭代后期，ωi的值变化幅度小，失去了对GOJaya 算法的影响。当r1，k，i和r2，k，i差值较大时，候选解改变幅度较大，对当前最优解继承程度较小，此时算法局部搜索能力差。在GOJaya算法中引入单纯形变换进行扰动，以解决算法迭代后期求解精度低的问题。以问题f为例，分别计算某一时刻当前最优解Xh，Xs，Xl的函数值fh，fs，fl。假设fs＞fl＞fh，对Xh，Xs，Xl进行单纯形变换。

（1）反射：首先计算出Xh，Xl的中心Xc，然后进行反射变换得到点Xr。若fs＞ft，将Xt替换Xs。

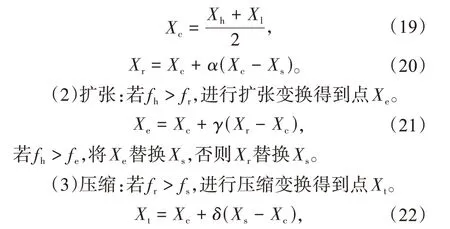
（4）收缩：若fs＞fr＞fh，进行收缩变换得到点Xw。

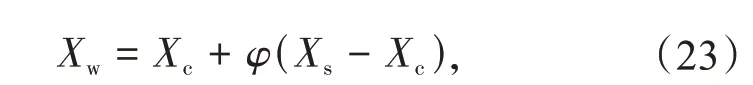
若fs＞fw，将Xw替换Xs，否则将Xr替换Xs。α，γ，δ以及φ为变换系数。

GOJaya 算法详细求解微电网优化目标f的流程如图2所示。

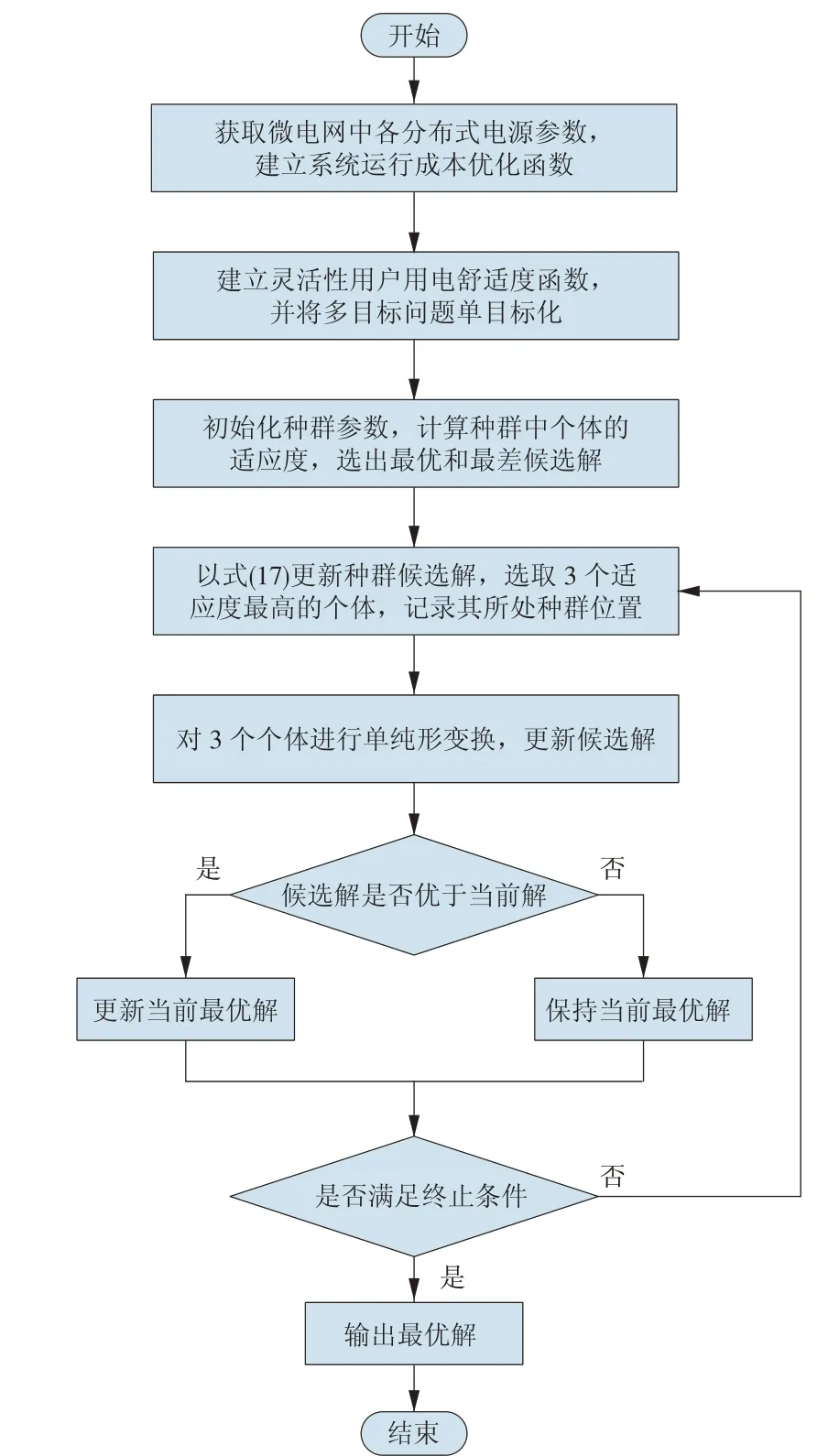
图2 GOJaya算法流程Fig.2 Flow chart of the GOJaya algorithm

GOJaya 算法引入ω以及单纯形变换后，在算法迭代前期ω变化幅度大，候选解改变幅度大，此时候选解对当前最优解继承度较小，候选解的搜索范围变大，加快了算法搜索到最优解附近的速度。算法迭代后期单纯变换增加了算法的局部搜索能力，进而更精准地找到问题最优解。

3 算例分析

3.1 算例概述

为了验证本文所提优化策略的有效性，本文搭建了如图3 所示的微电网仿真模型，该模型为改进的IEEE-33 节点测试系统［19-20］。微电网中各设备相关参数见表1。

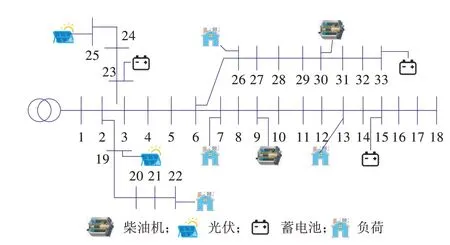
图3 微电网系统结构Fig.3 Structure of the microgrid system

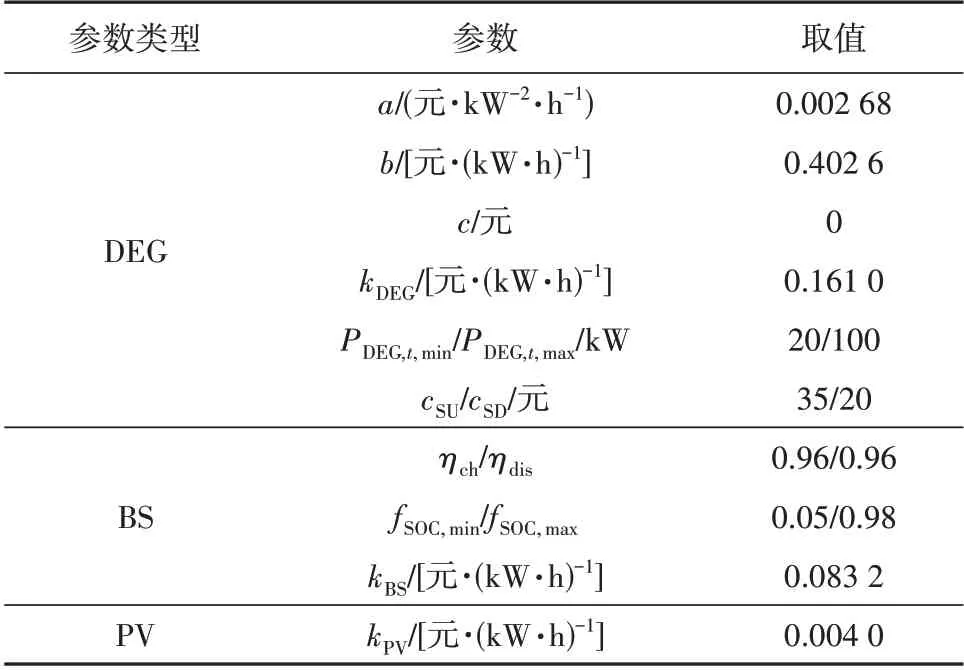
表1 微电网设备参数值Table 1 Parameters of devices in the microgrid

蓄电池初始容量为均为额定容量的50%。配电网分时电价见表2［20］。光伏出力以及用户原始用电分布如图4所示。

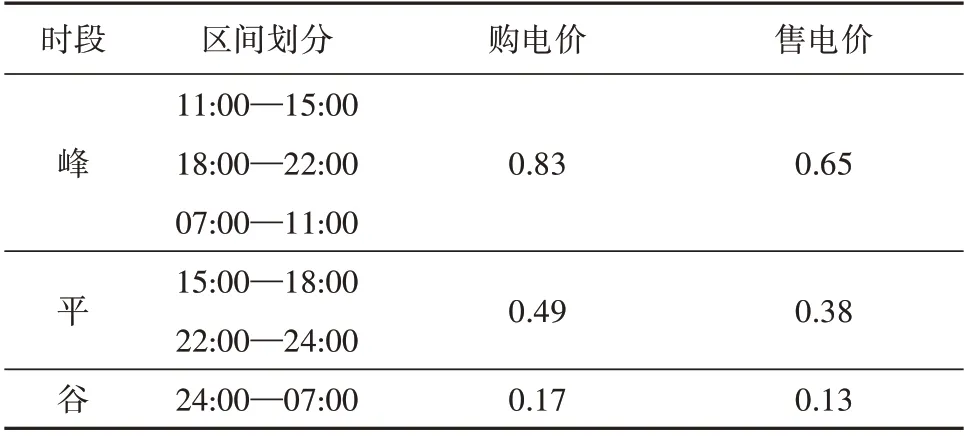
表2 分时电价Table 2 Time-of-use price 元（/kW·h）

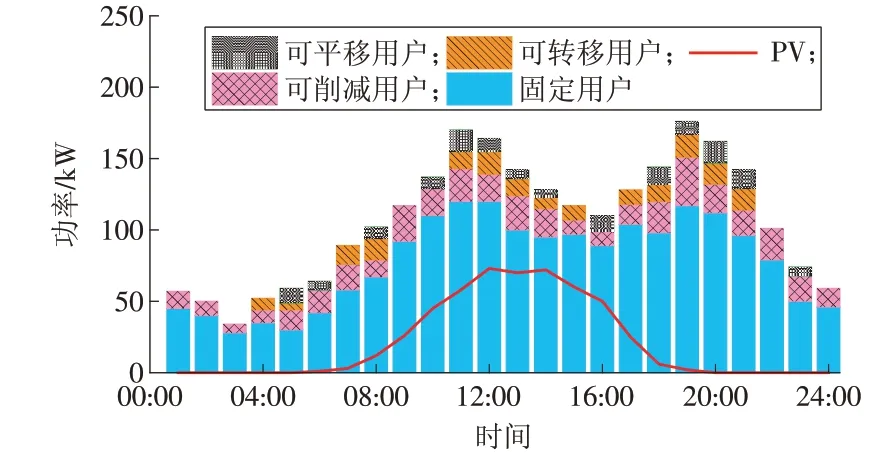
图4 光伏出力以及原始用户用电功率Fig.4 PV output and original user load

3.2 不同策略下分布式电源出力及灵活性用户用电舒适度对比分析

为了验证本文所提优化策略的优越性，本算例采用3种不同策略进行对比。

策略1：不考虑用户需求响应的优化策略。

策略2：考虑用户需求响应的优化策略。

策略3：本文提出的响应用户有限理性需求优化策略。

经过3种优化策略优化后微电网内部各设备出力结果以及灵活性用户的用电舒适度如图5、图6所示。3 种优化策略下的微电网各优化目标结果见表3。

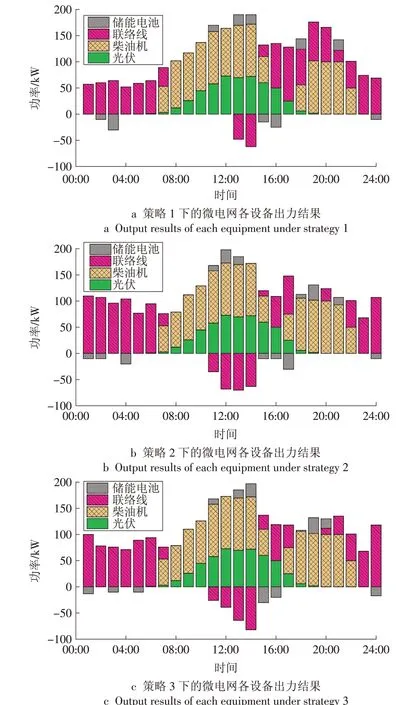
图5 3种优化策略下的微电网各设备出力结果Fig.5 Output of each equipment in the microgrid under three optimization strategies

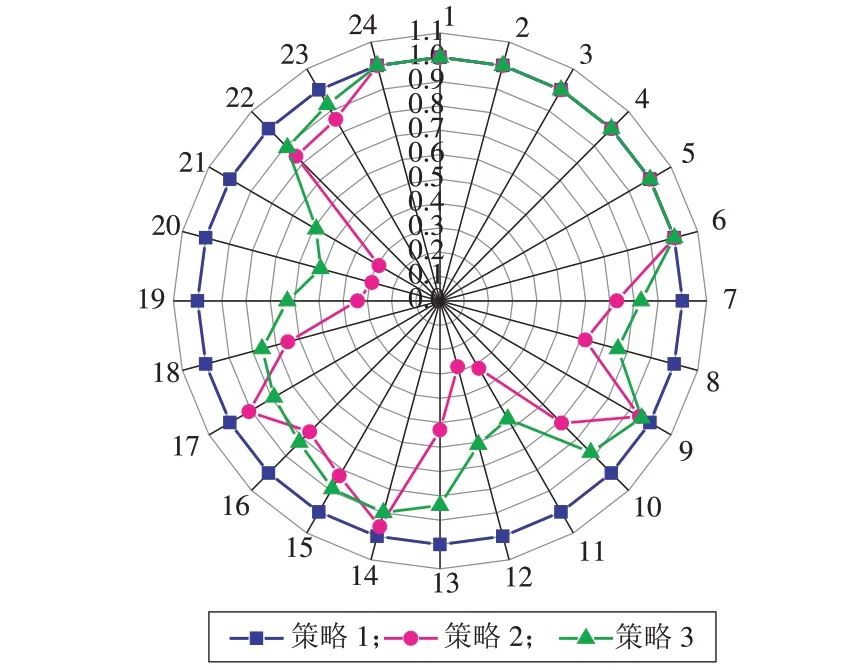
图6 3种优化策略下的灵活性用户用电舒适度Fig.6 Flexible-adjusted user comfort under three optimization strategies

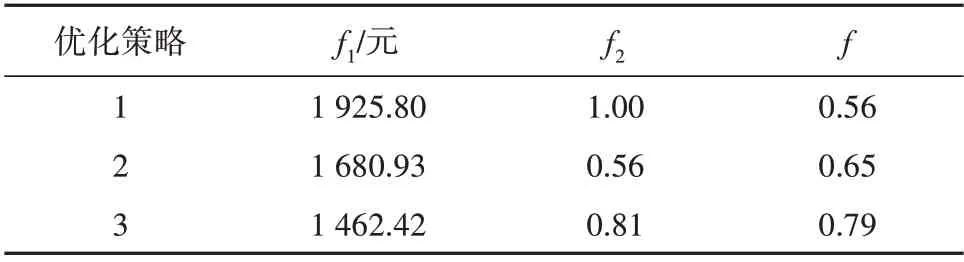
表3 3种优化策略下的各优化目标结果Table 3 Optimization objective results under the three optimization strategies

在11：00—14：00 时段配电网电价处于峰时段，从图5—6中可以看出策略2及策略3中的部分灵活性用户移到其他时段工作，然而策略3 中的用户受有限理性决策的影响并未将该时段所有灵活性用户移出该时段，因此该时段策略3 中的用户用电行为满意度优于策略2；柴油发电机在满足自身用户用电以外向配电网出售电能，以增加微电网自身的经济效益。同样，在18：00 —21：00 时段配电网电价处于峰时段，策略3 中的用户用电行为满意度仍优于策略2。该时段微电网内部用户用电较多，柴油发电机以及储能电池以最大出力不能满足用户的用电需求，需要额外向配电网购买电能，策略1下的微电网向配电网购买的电能大于策略2及策略3。在整个优化周期，策略3 中灵活性用户在降低系统以及自身用电成本的同时兼顾了用电行为满意度，起到了很好的削峰填谷及降低用电成本的作用。

在微电网运行成本方面，从表3 中可以看出策略3下的微电网运行成本最低。相比于策略1、策略2，策略3 下的微电网运行成本上分别减少了24.06%以及13.00%。在灵活性用户用电舒适度方面，可以看出策略2 未考虑灵活性用户用电决策的有限理性，因此策略2 中的灵活性用户用电舒适度最小。策略1 以及策略3 中灵活性用户用电舒适度分别高出策略2 中灵活性用户用电舒适度0.44 及0.25。在整体优化目标f上，策略3 明显优于策略1和策略2。从以上分析可以看出，本文提出的优化策略将多个优化目标融合一起，反映了用户真实用电行为。既降低了微电网的运行成本，也保证了灵活性用户较高的用电舒适度。

3.3 GOJaya算法性能对比分析

为了验证本文所提GOJaya 算法性能的优越性，分别选用遗传算法GA（Genetic Algorithm）［8］、Jaya 算法［18］以及GOJaya 算法进行对比试验。设3 种算法种群大小为100，最大迭代次数为500。单纯形变换中变换系数α取1，γ取2，δ取0.5，φ取0.5。微电网优化目标f1最优解的求解过程如图7 所示。求解的收敛时间、迭代次数以及大小见表4。

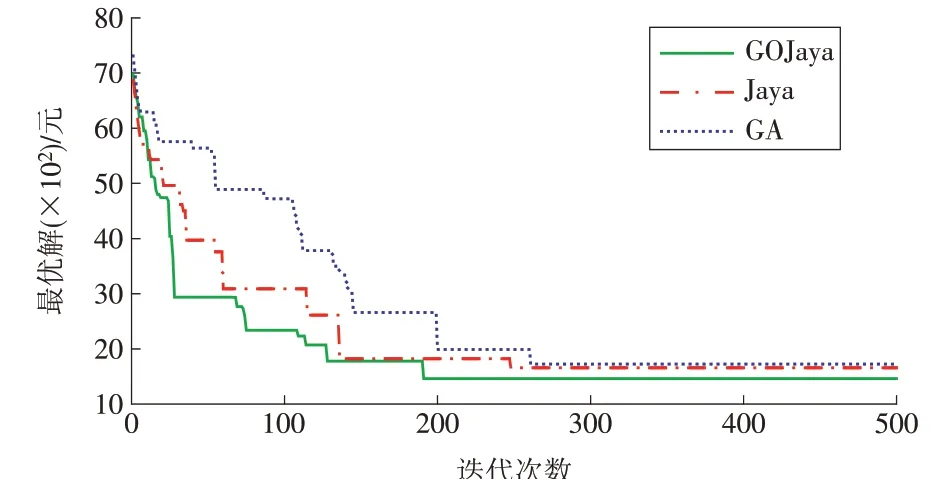
图7 3种算法求解过程Fig.7 Solution process of the three algorithms

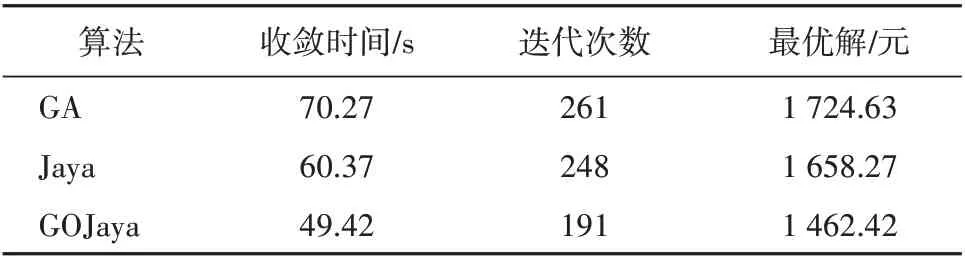
表4 3种算法性能对比Table 4 Performance of the three algorithms

由图7可知，GOJaya算法迭代前期收敛速度快，明显快于Jaya 及GA 算法，这是因为GOJaya 算法迭代前期非线性递减权重因子变化幅度大，候选解对于当前最优解继承程度较小，因此候选解的搜索范围较大，加快了GOJaya 算法的求解速度，使得候选解很快的到达最优解附近。由表4可知，与GA，Jaya算法相比，GOJaya 算法在收敛时间上分别减少了42.19%，22.16%；在迭代次数上分别减少了36.65%，29.84%。在迭代后期单纯形变换增加了GOJaya 算法的扰动能力，增加了算法的求解精度。试验结果表明，本文提出的GOJaya算法在收敛速度上以及收敛精度上均优于GA，Jaya算法。