基于纵横交叉算法-门控循环单元的日前电价预测模型
2022-12-27翟广松王鹏梁鹏勋谢智锋殷豪
翟广松,王鹏,梁鹏勋,谢智锋,殷豪
(广东工业大学自动化学院,广州 510006)
0 引言
随着电力市场的发展,市场耦合范围不断扩大,新能源渗透率不断提高,使得电价变得更加复杂,价格波动更加强烈,建立高准确率的电价预测模型面临着前所未有的挑战[1]。
目前,电价预测方法主要有统计方法与人工智能方法。统计方法包含差分自回归移动平均(Autoregressive Integrated Moving Average,ARIMA)法[2]、广义自回归条件异方差(Generalized Autoregressive Conditional Heteroskedasticity,GARCH)法[3]等,这些方法基于线性模型预测,对非线性电价序列的预测效果难以达到满意的程度。人工智能方法主要有机器学习法和深度学习法。机器学习法包括极限学习机(Extreme Learning Machine,ELM)[4]、支持向量机(Support Vector Machines,SVM)[5]以及神经网络[6]等。相比于机器学习法,深度学习法拥有更为强大的学习能力和特征提取能力。在深度学习模型中,循环神经网络(Recurrent Neural Network,RNN)类更善于处理时序相关问题。文献[7]使用RNN实现了电价的预测,由于RNN存在梯度消失问题,采用长短时记忆(Long-Short Term Memory,LSTM)网络、门控循环单元(Gated Recurrent Unit,GRU)作为RNN 的改进模型,很好地解决了该问题。文献[8]采用纵横交叉(Crisscross Optimization,CSO)算法优化LSTM 网络参数,表明了对网络参数进行优化的可行性。文献[9]表明,相比于LSTM 网络,GRU 内部结构更为简单且高效,但传统GRU 采用梯度下降法更新参数,易陷入局部最优,存在不稳定性的问题。
电力市场条件下,电价的影响因素包括生产、负荷、新能源发电量[10]、市场耦合[11]、天气、人类社会活动等。现有的电价预测研究往往只考虑少数几种特征,建模数据不完全,未能充分考虑电力市场的多维特征因素。但过多的输入特征会带来信息冗余、模型训练困难与过拟合等问题,影响电价预测结果,比如天气、人类社会活动因素不直接影响电价,但会影响电力的供需。
针对电价波动性大的特点,采用模式分解方法将电价分解为若干平稳分量后分别进行建模预测,再将各分量预测结果叠加得到最终预测电价的方法有利于提升电价预测精度。但小波变换[12]、经验模 式 分 解[13]、集 合 经 验 模 式 分 解(Ensemble Empirical Mode Decomposition,EEMD)[14]等分解方法存在自适应性差、模态混叠等问题,而变分模态分解(Variational Mode Decomposition,VMD)是一种自适应、非递归分解方法,具有较强的可靠性与鲁棒性[15-16]。
针对以上问题,本文提出一种基于CSO-GRU的日前电价预测模型。首先利用互信息(Mutual Information,MI)方法分析电价与各特征之间的相关性,提取与电价相关性较高的特征,同时利用VMD方法将电价序列分解为若干分量;然后将各分量分别叠加提取的特征送入GRU 模型进行预测,利用CSO优化模型的部分参数,避免模型陷入局部最优;最后,将各分量预测结果叠加得到最终预测电价。选取北欧Nordpool 电力市场的运营数据进行试验,以验证该模型的预测精度。
1 模型基本原理
1.1 MI方法
MI 可度量变量间的线性和非线性关系,反映2个变量的相关程度[17],MI 值越大,说明变量间的相关性越强。本文采用MI 方法评估电价与各特征间的相关程度,选取MI值较大的特征作为预测模型的输入。
MI定义为

1.2 VMD方法
VMD 是一种自适应、完全非递归的分解方法,具有较强的可靠性和鲁棒性。本文采用VMD 方法将电价序列分解为若干分量,步骤如下。
(1)将模态uk(t)进行Hilbert 变换,得到单侧频谱

式中:{uk}={u1,u2,…,uk}为分解后的k个模态分量;{ωk}={ω1,ω2,…,ωk}为各模态对应的中心频率;α取100。
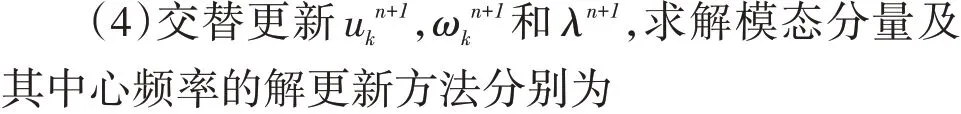
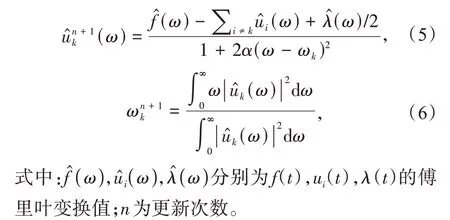
1.3 CSO算法
CSO 算法是一种智能优化算法,包含横向交叉和纵向交叉2种方式[18]。横向交叉更新公式如下
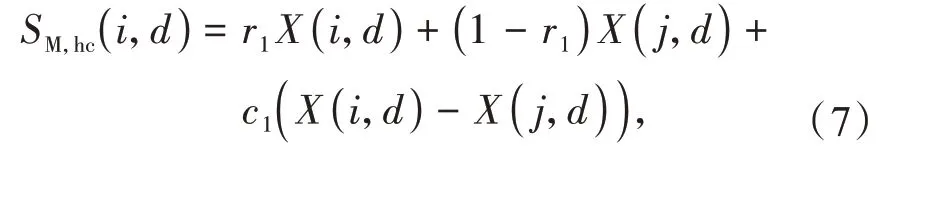

式中:r1,r2为在[0,1]均匀分布的随机数;c1,c2为在[-1,1]均匀分布的随机数,且c1,c2所在项为边缘搜索项;X(i,d),X(j,d)分别为父代粒子X(i),X(j)的第d维;SM,hc(i,d),SM,hc(j,d)分别为粒子X(i),X(j)在第d维交叉产生的子代。
纵向交叉更新公式为
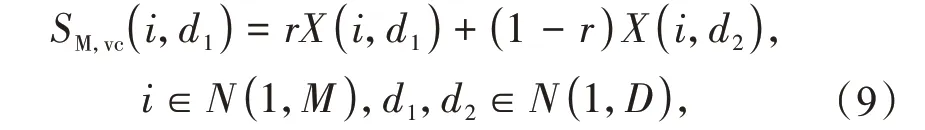
式中:X(i,d1),X(i,d2)分别为粒子X(i)的第d1维和第d2维;r为均匀分布在[0,1]的随机数;SM,vc(i,d1)为粒子X(i)在第d1,d2维交叉产生的子代。
1.4 GRU
GRU 作为循环神经网络的变体,与LSTM 一样,继承了循环神经网络善于处理时间序列数据的优势;同时,通过增加门控机构控制信息的传递,解决了循环神经网络梯度消失的问题。电价时间序列具有一定的时序相关性,GRU 能学习到这种隐藏关系,本文利用GRU作为电价基准预测模型。
LSTM 包含遗忘门、输入门与输出门,而GRU 将遗忘门与输出门优化合并为一个门,只包含重置门与更新门。相比LSTM,GRU 的结构更为简单且效率更高。在GRU 单元中,重置门rt用于控制当前输入与历史记忆信息的融合,更新门zt决定留下记忆信息的量,其内部结构如图1所示。
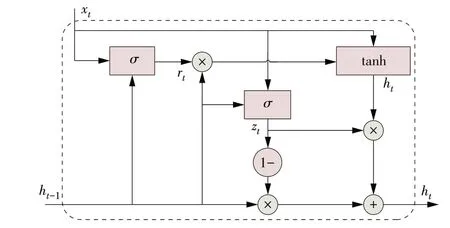
图1 GRU单元内部结构Fig.1 Internal structure of a GRU unit
某一时刻,GRU 通过接受当前输入xt和上一时刻状态ht-1,通过下式得到汇总h͂t并更新输出ht。
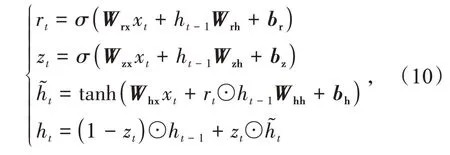
式中:σ为Sigmoid 激活函数;Wrx,Wrh,Wzx,Wzh,Whx,Whh均为权重矩阵;br,bz,bh均为偏置向量;⊙为点乘运算。
2 组合模型的构建
电价的影响因素众多,本文考虑了生产、负荷、风电、计划流量、市场容量、市场耦合等因素,利用MI 方法提取电价相关性较高的特征作为模型的输入。由于电价序列具有较强的波动性与非平稳性,直接建模的预测效果不佳,利用VMD对电价进行分解并利用CSO 优化后的GRU 模型分别对各分量进行预测并叠加,具体步骤如下。
(1)利用MI方法评估各个特征与电价之间的相关性,提取电价相关性较高的特征。
(2)利用VMD将电价分解为若干固有模态函数(Intrinsic Mode Function,IMF)分量,分别与高相关性特征结合构成模型输入。
(3)对各分量分别建立GRU 模型并进行训练,利用CSO 对训练好的GRU 模型输出层的权值和阈值参数进行优化。
(4)将各分量的预测结果相加,得到最终的电价预测值。
MI-VMD-CSO-GRU 模型框架如图2所示。
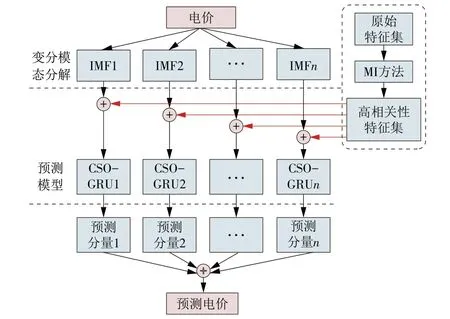
图2 MI-VMD-CSO-GRU 模型框架Fig.2 Framework of the MI-VMD-CSO-GRU model
步骤(3)所搭建的GRU 预测模型如图3 所示。日前电力市场需提前一天提供翌日24 h 电价,本文通过搭建多输入-多输出预测模型,输入前一天的电价与高相关性特征,输出预测日电价。
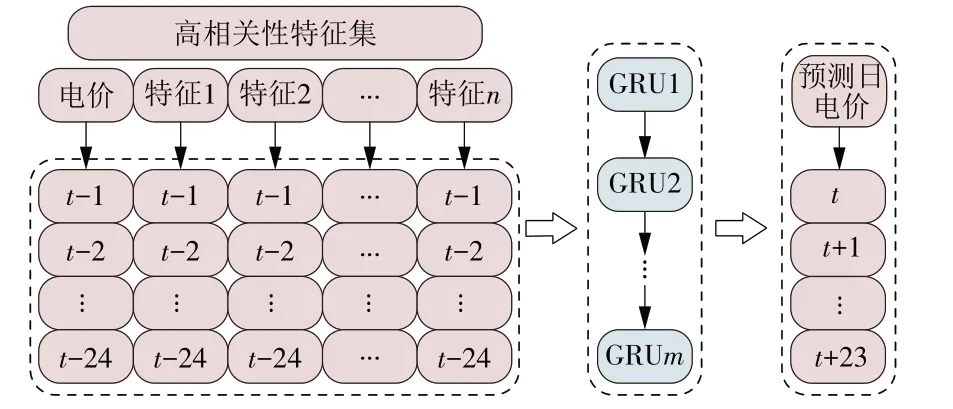
图3 GRU预测模型Fig.3 GRU prediction model
传统GRU 采用梯度下降法更新参数,为避免GRU 模型陷入局部最优,利用CSO 对常规训练好的GRU 模型输出层的权值和阈值进行优化,CSOGRU流程如图4所示。

图4 CSO-GRU流程Fig.4 Framework of the CSO-GRU model
3 算例分析
试验选取北欧Nordpool 电力市场2016 年3 月21 日—5 月14 日的日前电价及其相关特征实测数据,电价特征量包括生产、负荷、风电、计划流量、市场容量、市场内部各国的净交换电量(瑞典、挪威、丹麦、芬兰、立陶宛、拉脱维亚、爱沙尼亚)、与外部市场的交换电量(挪威价区2-荷兰、瑞典价区4-德国、丹麦价区1-德国、丹麦价区2-德国),共计16 维特征。数据采样频率为1 h,共计1 320组数据,划分前1 080 组数据为训练集,后240 组数据(即最后10 d)为测试集。
为避免数据之间的量纲差异影响预测精度,根据式(11)将数据归一化映射到[0,1]。
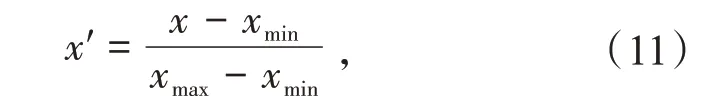
式中:x'为归一化值;x为实际值;xmax和xmin分别为最大值和最小值。
试验中的参数设置为:GRU 模型包括一个神经元数为8 的隐含层,输出层为全连接(Dense)层,优化算法为Adam,损失函数为均方误差(Mean Squared Error,MSE),激活函数为ReLU 函数,迭代次数为500。优化过程中,设置CSO 的横向交叉概率为1.0,纵向交叉概率为0.6,种群数目为20,最大迭代次数为250,适应度函数选用MSE,即优化目标为较小的MSE
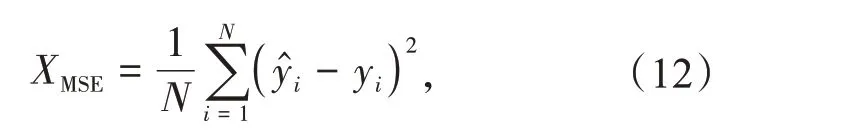
式中:N为样本数目;y为电价真实值;ŷ为电价预测值。
选用均方根误差(Root Mean Square Error,RMSE)、平均绝对误差(Mean Absolute Error,MAE)和对称平均绝对百分比误差(Symmetric Mean Absolute Per Centage Error,SMAPE)来评价各个预测模型的预测精度,公式如下
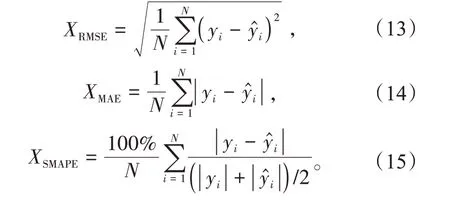
3.1 MI方法有效性验证
为了验证MI方法在电价预测问题上的有效性,分别采用不降维方法、当前较流行的主成分分析(Principal Components Analysis,PCA)方法以及MI方法对原始特征集进行处理,并搭建GRU 模型进行预测。各特征与电价之间的MI 值见表1,不同降维方法的预测误差见表2,不同预测模型的电价预测结果如图5所示。
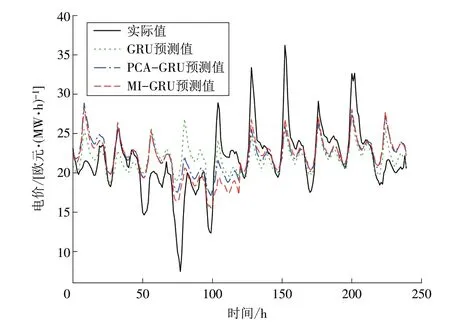
图5 不同预测模型的电价预测值Fig.5 Electricity prices predicted by different models
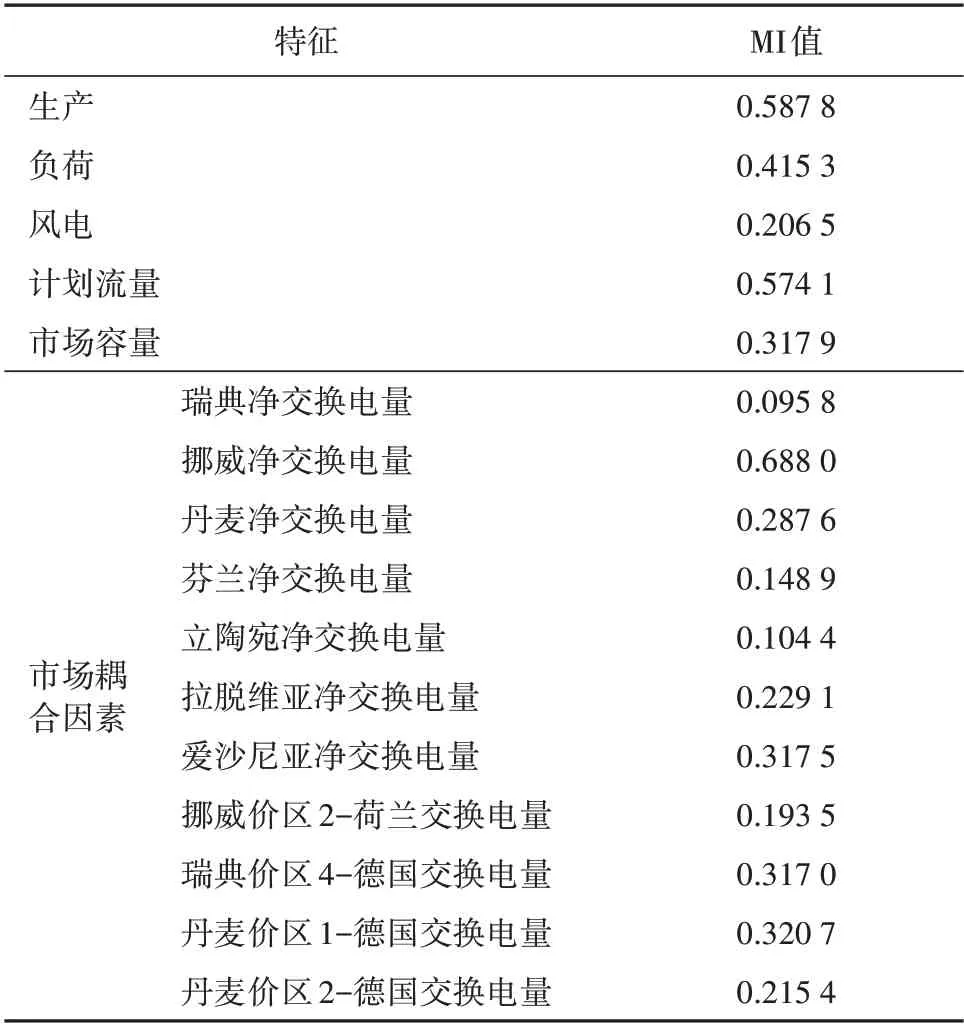
表1 各特征与电价之间的MI值Table 1 MI value between different features and electricity price

表2 不同降维方法的预测误差Table 2 Prediction errors under different dimensionality reduction methods
MI值越大,说明特征与电价之间相关度的概率分布“贡献率”越大,本文特征选取的判断阈值为0.5。由表1可以看出,挪威净交换电量、生产、计划流量这3 个特征量与电价之间的相关性较强,可选作电价预测模型的输入特征。
由表2 和图5 可以看出:相比于不降维的GRU模型,采用降维方法的组合模型预测准确率更高,PCA-GRU 和MI-GRU 模 型 的XRMSE分 别 降 低 了10.75%,11.15%,XMAE分别降低了7.67%,9.63%,XSMAPE分别降低了9.82%,11.05%,说明选取对电价预测更为重要且输入维数较小的特征,可以降低建模难度,提高电价预测精度;采用MI-GRU模型的预测误差相比PCA-GRU 模型更小,原因在于PCA 方法度量的是变量间的线性关系,而MI方法可以度量变量间的线性与非线性关系,MI 评估结果更为准确,验证了MI方法在电价预测问题上的有效性。
3.2 VMD方法有效性验证
为验证VMD方法在电价预测问题上的有效性,分别采用不分解法、EEMD 法及VMD 法将原始电价分解为若干分量,然后将各分量分别叠加提取的特征送入GRU 预测模型进行预测,将各分量预测结果叠加得到最终的预测电价。大量试验表明,EEMD分解层数为6、VMD 分解层数为5 时,组合模型预测效果最好。VMD 分解结果如图6 所示,不同分解方法的预测误差见表3,电价预测结果如图7所示。
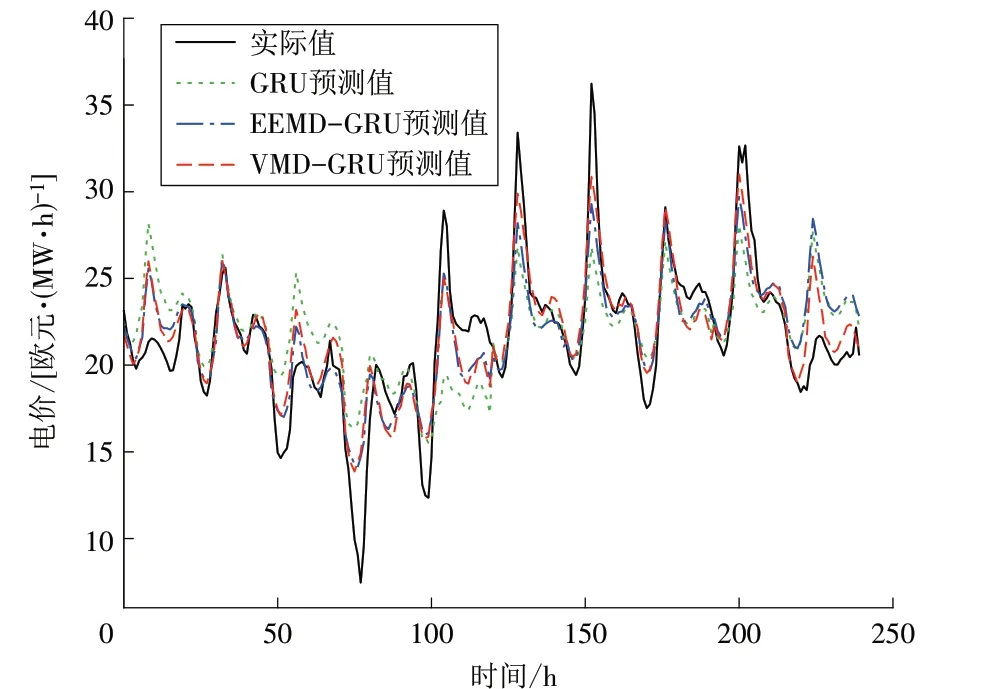
图7 不同分解方法的电价预测值Fig.7 Electricity prices predicted by different decomposition methods
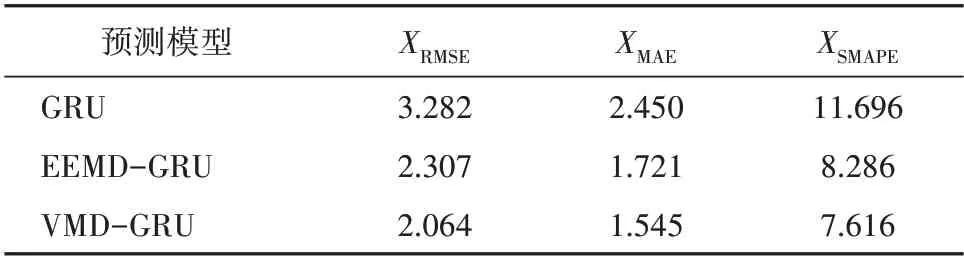
表3 不同分解方法的预测误差Table 3 Prediction errors under different decomposition methods
图6 可以看出:利用VMD 方法将电价序列分解为若干相对平稳的细节分量和趋势分量,可以更清晰地掌握电价的不同周期特性,有助于降低电价预测难度(图中:RES为剩余分量)。
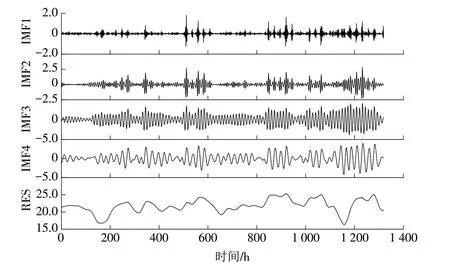
图6 VMD分解结果Fig.6 Decomposition results of VMD
由表3 和图7 可以看出:相比于不分解的GRU模型,采用分解方法的组合模型准确率更高,EEMD-GRU 和VMD-GRU 模型的XRMSE分别降低了29.71%,37.11%,XMAE分 别 降 低 了 29.76%,36.94%,XSMAPE分别降低了29.16%,34.88%,说明通过模式分解方法可以掌握电价的不同周期特性,降低电价的波动性,从而提高电价预测精度;采用VMD 方法组合模型的预测误差相比EEMD 方法要小,原因在于EEMD方法采用递归分解方式,可能出现模态混叠问题,而VMD 方法采用非递归分解方式,可靠性和鲁棒性较好,验证了VMD 方法在电价预测问题上的有效性。
3.3 CSO-GRU有效性验证
为了验证CSO-GRU 预测模型的有效性,分别采用基于MI-VMD 方法的BP 神经网络,RNN,LSTM,GRU,CSO-GRU 模型进行预测,不同模型的预测误差见表4,电价预测结果如图8所示。
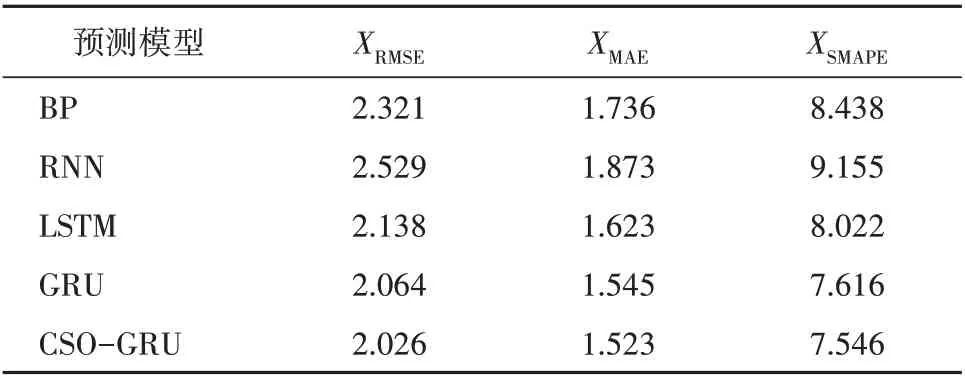
表4 不同模型的预测误差Table 4 Prediction errors of different models
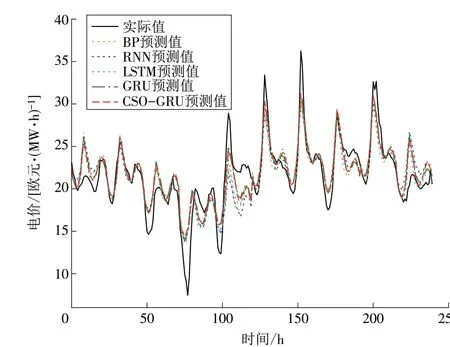
图8 不同模型的电价预测值Fig.8 Electricity prices predicted by different models
由表4和图8可以得出以下结论。
(1)GRU 作为RNN,LSTM 的改进模型,能更好地挖掘电价序列的时间规律,电价预测精度更高。与BP,RNN,LSTM 模型相比,GRU 模型的XRMSE分别降低了11.07%,18.39%,3.46%,XMAE分别降低了11.00%,17.51%,4.81%,XSMAPE分别降低了9.74%,16.81%,5.06%。
(2)CSO-GRU 作为GRU 的改进模型,经CSO 优化GRU 模型的权值和阈值参数后,模型的预测精度得到了一定程度的提高,这得益于CSO 独特的双交叉机制,横向交叉操作中的边缘搜索行为减小了搜索盲区,增强了模型的全局搜索能力,不同维度上的纵向交叉操作避免了模型陷入局部最优。相比于GRU 模型,CSO-GRU 模型的XRMSE,XMAE,XSMAPE分别降低了1.84%,1.42%,0.93%。
(3)本文所提CSO-GRU 预测模型的各项误差均为最小,相比于BP,RNN,LSTM,GRU 模型,CSOGRU 模 型 的XRMSE分 别 降 低 了12.71%,19.89%,5.23%,1.84%,XMAE分别降低了12.27%,18.69%,6.16%,1.42%,XSMAPE分别降低了10.57%,17.58%,5.93%,0.93%,验证了所提CSO-GRU 模型在电价预测问题上的有效性。
4 结论
针对电价特征数目增多和电价波动性大的问题,本文综合考虑了多种电价因素进行建模,提出了一种基于互信息、变分模态分解和纵横交叉算法优化门控循环单元(MI-VMD-CSO-GRU)的日前电价预测方法。通过算例分析,主要结论如下。
(1)采用MI 方法选取电价的高相关性特征,在保证足够信息量的同时降低了输入特征维度,降低了建模难度,提高了预测精度。
(2)采用VMD方法将电价序列分解为若干相对平稳的细节分量和趋势分量,从而掌握了电价的不同周期特性,可有效提升预测准确率。
(3)GRU 网络具有较好的电价预测效果,采用CSO 算法优化GRU 网络的权值和阈值参数,可提升模型稳定性和跳出局部最优的能力,从而提高模型的预测精度。
该方法组合了多种算法的优势,提高了电价预测精度,具有良好的应用前景。
