基于综合可调度潜力评估的电动汽车优先调度策略
2022-12-27李昊季振亚刘晓峰张仕玮包宇庆王维
李昊,季振亚*,刘晓峰,张仕玮,包宇庆,王维
(1.南京师范大学电气与自动化工程学院,南京 210023;2.江苏省气电互联综合能源工程实验室,南京 210023)
0 引言
党的十九届五中全会首次将碳达峰和碳中和目标纳入“十四五”规划建议。在近年来全球节能减排的大趋势下,电动汽车(EV)作为以电力为能源的新一代绿色交通工具迅速发展。大规模EV 的充电负荷成为电网运行中不可忽视的影响因素[1]。研究结果表明,有序充电可为运营商及用户带来丰厚的经济效益[2-4]。而随着EV 规模扩大,参与调度的EV 数量增多,电网对单个EV 分别下发控制指令所伴随的计算与传输量增大[5-6]。如何在保证电网侧需求响应的情况下,减少对EV 的调度次数、提高调度效率、节约调度成本,对电网有着重要的意义。
为提高EV 调度效率、减少调度成本,文献[7]定义了“电动汽车与电网互动(V2G)可用容量”的概念,基于EV 的电池充、放电状况与行为概率模型,对各集群V2G 可用容量进行了实时评估。文献[8]提出了“可调度能力”概念,从用户侧角度考虑了EV自身电池损耗、可放电能力以及用户信用度,构建EV 可调度能力评估体系,并提出EV 日内优先调度策略模型。以上2 种评估均对EV 调度具有较好的效果,但评估方法仅对汽车或用户本身的特征进行分析,并未考虑电网侧需求,在不同特征的基础负荷中适用性略显不足。
目前,多种调度模型以各EV 充电行为概率分布信息已知且完备为前提,简化模型求解,忽视了EV 区域之间的流动性与随机性[9-10]。文献[11-14]通过数据驱动的方式考虑变量的随机性:文献[12]在综合能源领域使用场景生成与削减技术,对多种随机输入变量进行合理利用,减少用能成本;文献[13]使用原始生成对抗网络(Generative Adversarial Network,GAN)技术,在保留EV 流动特性的情况下,对不全面EV 负荷数据进行修补,提高EV 负荷预测上的精度;文献[14]验证了对单个EV 调度将造成计算时间的剧增,并使用k-means 二次聚类方法构建EV 调度模型,证明以EV 群体为调度单位可以减少调度时间。
在以上研究的基础上,本文从用户侧及电网侧2 个角度出发,对不同群体的可调度能力与调度效益进行评估,构建综合可调度潜力评估模型,并根据评估结果划分优先调度区、下发调度指令。考虑区域内EV 流动性,使用基于W-GAN(Wasserstein-GAN)与k-means 聚类算法的EV 群体分类方法,在保留EV 流动性的同时,提高大规模电动汽车接入时的模型求解速度。最后,通过削峰填谷算例验证所建评估模型划分的调度优先区域对减少EV 调度数量的有效性。
1 基于EV综合可调度潜力评估的优先调度方法框架
综合可调度潜力评估模型由可调度能力与调度效益2 部分构成,分别对应电动汽车侧与电网侧角度的评估,并通过熵权法确定其权重。根据评估结果对EV群体划分优先调度区域。
从用户侧出发,电动汽车充电的能力与其自身属性以及充电需求有关,需求的紧急程度主要分为目的地充电需求以及紧急充电需求[15]。目的地需求下的EV 停放时间较长,其可接受调度能力大小与EV 自身入/离网电池荷电状态(SOC)、电池容量等能量特征有关;在紧急需求下,EV停留时间有限,可接受调度能力受停留时间约束较大。
从配电网角度出发,其在负荷峰谷处对EV 的放电及充电需求较大,因此可定义EV 的调度效益评估指数,通过判断EV 在网时段对应的负荷水平,确定此时对电网进行调度的效益。
在模型求解过程中,若对每辆EV 均进行综合可调度潜力评估,则大规模EV 的接入需要高维度计算求解模型[16],使得调度策略求解困难。考虑到GAN技术处理流动性数据的优势[13,17]以及聚类算法对于减少计算时间的优势[14],本文提出一种基于W-GAN 算法与k-means 聚类算法的EV 群体分类方法,基于EV 流动行为上的相似性进行群体划分,从而将对单辆电动汽车的评估转换为对具有相同出行规律群体的综合可调度潜力评估,从而减少计算量。
2 EV可调度潜力评估模型
2.1 可调度能力评估
在满足EV 自身需求的基础上,其与电网可互动电量即为停留时间内除去自身需求的可充入电量[7]。则各EV群体可调度能力评估指数可定义为
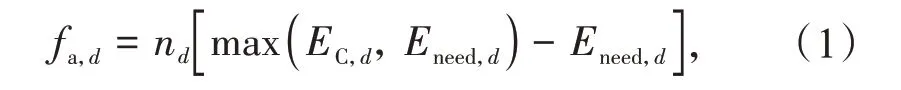
式中:nd为群体d中电动汽车的数量;EC,d为群体d平均停留时间内的可充入电量;Eneed,d为群体d平均需求电量。

式中:PC,d为平均充电功率;η为充/放电效率;TA,d,TD,d分别为群体d内EV 聚合中心的入网时间和离网时间;SOC,0,d为群体d内EV 入网时动力电池的平均荷电状态;SOC,E,d为群体d内EV 用户离网时平均期望荷电状态;En,d为d内EV 平均电池容量;εd为协商系数,调度中心或聚合商可与EV 用户进行不同程度的协商,从而延长一定时间的停留时间。
当fa,d>0 时,表示 群 体d内的EV 可调 度,fa,d越大,其可接受调度能力越强;当fa,d≤0时,表示该群体内EV 不宜接受调度,且fa,d越小,表明该群体内EV的充电需求越紧急,应优先进行补电。
2.2 调度效益评估
群体d下EV标准化的调度效益指数定义为
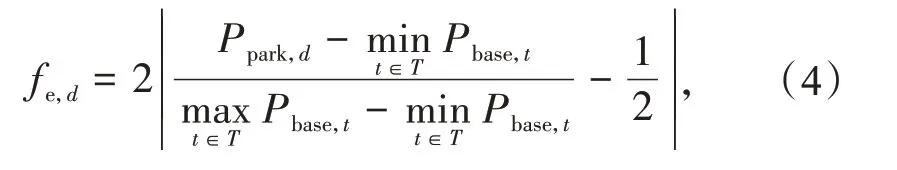
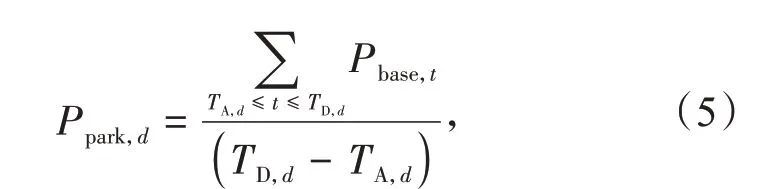
式中:T为最小调度周期;t为当前时间;Pbase,t为t时刻的基本负荷;Ppark,d为群体d停留时间内的基础负荷平均值。fe,d越大,表明EV 充电时越接近基础负荷的极端值,其调度效益也越高。
2.3 综合可调度潜力评估模型
综合潜力评估模型由可调度能力评估与调度效益评估2部分综合而成。在一般的多参数评估模型中,为防止不同量纲参数对评价结果造成的影响程度不同,需对参数去除量纲。
对可调度能力评估指数fa,d做无量纲化处理,得到
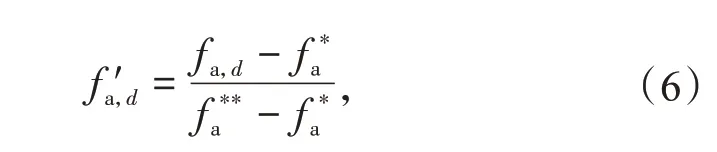
式中:f**a为所有场景下fa,d的最大值;f*a为所有场景下fa,d的最小值,同时f'a,d∈[0,1]。同理,fe,d对应的无量纲指数f'e,d可参照式(6)求出。
在对EV 可调度潜力进行综合评估时,需要将可调度能力评估指数与可调度效益评估指数相结合。为了客观确定2种指标参与潜力评价时的权重值,引入熵权法进行权值计算。
可调度能力指标的熵值为ea,d,
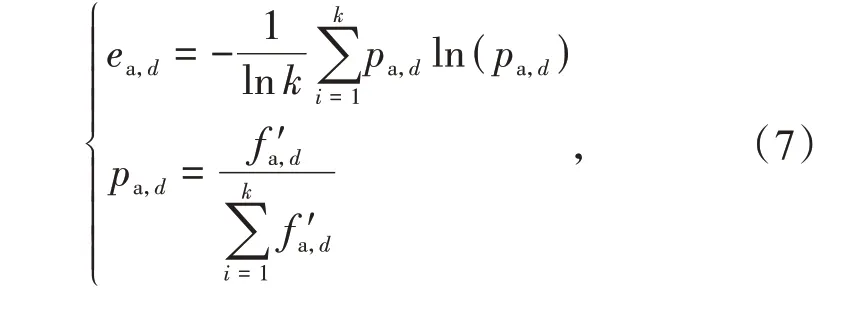
式中:k为电动汽车群体的数量;pa,d为群体d的指标f'a,d的评价值。
同理,可调度效益指标的熵值为ee,d,其评价值为pe,d。因此,该区域中指标f'a,d与f'e,d的熵权分别为

最终得到群体d内EV 的综合可调度潜力评估指数
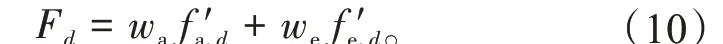
Fd越高,则代表该群体中此EV 参与调度时,用户侧与电网侧的综合效益越高。
2.4 综合可调度潜力评估阈值确定
为提供更直观的调度参考,应设置一定的参考阈值,传统的阈值设定往往采用单一阈值线的方式。但考虑到随着聚合数目的增长,EV群体内成员的充电行为特征将呈现更多的不确定性,若设置某一阈值线,可能面临部分群体的综合可调度潜力评估值经常在阈值线两侧徘徊,这样的调度不确定性可能会给EV用户造成困扰。
因此本文采用三级阈值的方式,设置优先调度区、备用调度区以及不宜调度区。基于标准化方法的可调度阈值指数Qd∈[0,1],

所有场景中Fd最大的EV 群体可调度阈值指数为1,可进行最优先调度;Fd最小的EV 群体可调度阈值指数为0,表明其最不宜参与调度。通过标准化的Qd,保证至少存在1 组EV 群体处于可调度状态。
在剩余可调度电动汽车群体中,根据实际配电网需求紧急情况,设置备用区可调度阈值线
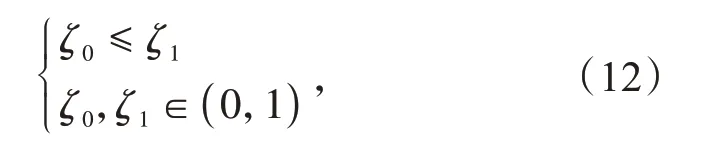
式中:ζ1,ζ0为备用调度区可调度阈值的上、下限。当ζ0=ζ1时,表明不设置备用可调度区域,此时可将其作为可调度与不可调度的临界状态,根据该区域几日内临界状态附近电动汽车群体的跨线变化状态,灵活制定其备用调度区可调度阈值范围。ζ1-ζ0越小,表明临界状态附近电动汽车群体内成员充电行为特征越稳定。
基于电动汽车综合可调度潜力评估的优先调度方法框架如图1 所示(其中群体1—4 的综合可调度潜力评估指数为F1,F2,F3,F4)。
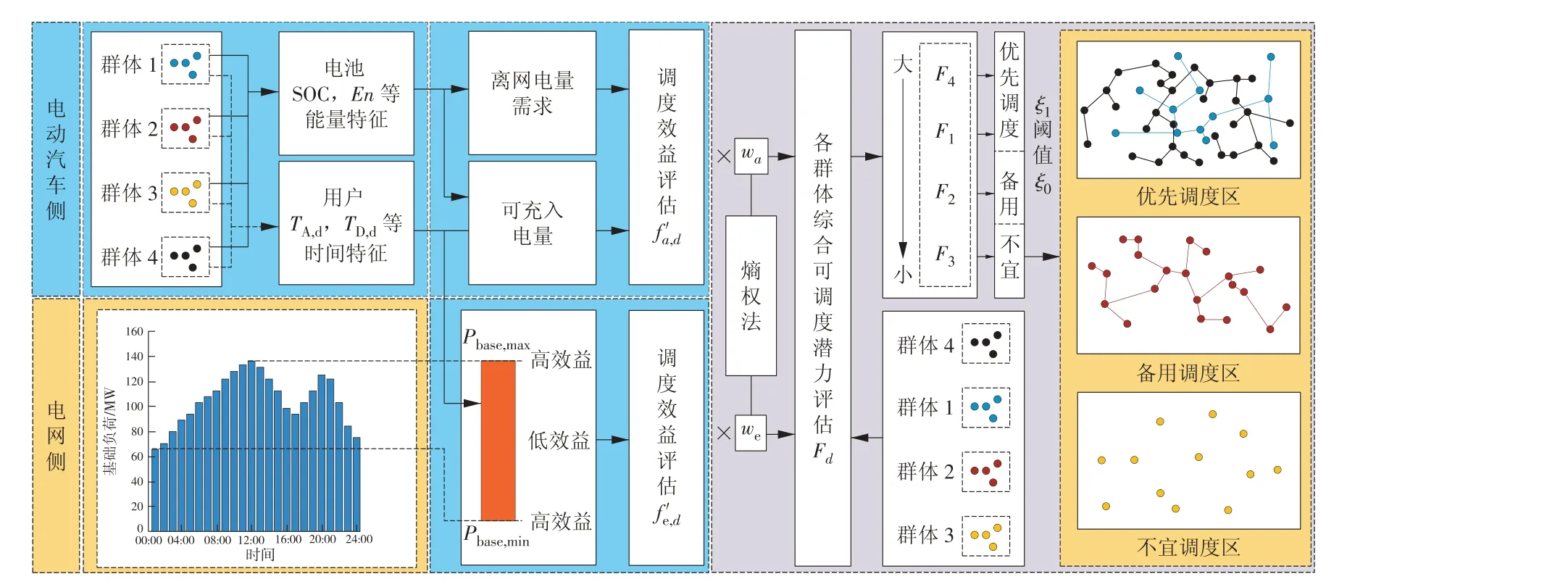
图1 基于电动汽车综合可调度潜力评估的优先调度方法框架Fig.1 Framework of the priority scheduling method based on comprehensive dispatchable potential assessment for EVs
3 考虑可调度潜力评估的EV削峰填谷策略
3.1 目标及约束
削峰填谷控制目标实质是令负荷曲线尽量平滑[7]。传统的削峰填谷策略通常采用最小化负荷曲线方差的方式[18],但该非线性化目标函数难以采用分段线性化方法求解,在某些约束条件的限制下难以收敛。因此,本文采用负荷参考曲线法[19]进行削峰填谷优化调度,即为使总负荷贴近目标负荷曲线的过程,其目标函数为
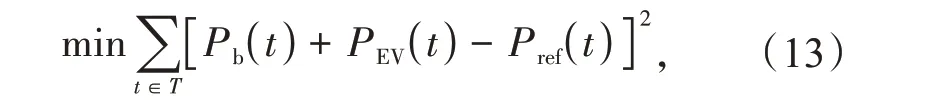
式中:Pb(t)为t时刻基础负荷;PEV(t)为t时刻电动汽车充放电负荷;Pref(t)为t时刻削峰填谷目标。
相关的约束条件见式(14)—(15)。
放电功率约束为
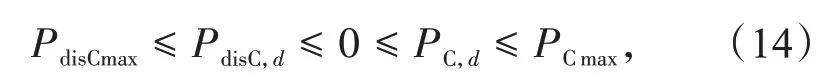
充电过程中的SOC约束为
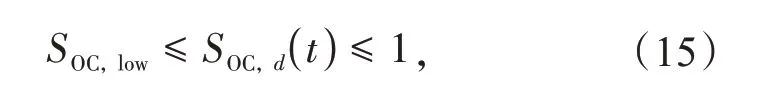
式中:PdisC,d为d内电动汽车平均放电功率;PCmax与PdisCmax分别为电动汽车最大充、放电功率限制,充电为正,放电为负;SOC,d(t)为任意时刻群体d中EV 荷电状态;SOC,low为对EV调度的最低荷电水平。
3.2 削峰填谷调度策略
以某基础负荷达到峰值的时段为例,该峰时段电动汽车总的放电需求电量为

式中:Pdneed(t)为t时刻的放电负荷需求,时间t∈[tout,tin],tout,tin分别为基础负荷开始超出和进入目标负荷区域的时间。
此时,恒功率放电下,该时间段群体d中所有EV所能完成的放电量为

式中:nd为d中EV的数量。
则处于优先调度区、备用调度区的EV 能完成的放电量分别为
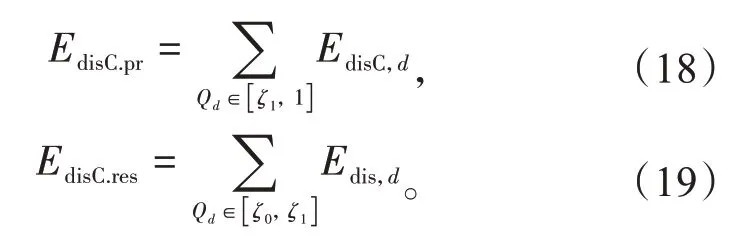
根据所需求的Edneed(tout)与各区能完成的放电量进行削峰填谷策略安排。各电动汽车群体电动汽车放电功率PdisC.d可表示为[16]

式中:EdisC.total为总可放电容量,根据可调度潜力确定的区进行分级;Δt为计算的最小时间间隔;ΔEpeak(t)为t时刻开始Δt内需要完成的削峰电量。
(1)若Edneed(tout)≤EdisC.pr,仅需要优先调度区的EV即可完成削峰任务,则其总可放电容量定义为

(3)若EdisC.pr+EdisC.res<Edneed(tout),则需要对不宜调度区的EV 进行调度。为减小不宜调度区EV 的调度,无论该区是否能够完成削峰任务,都可将削峰总需求分摊给全部EV,即

为保证各EV 群体中EV 离网时的SOC 水平,对各群体下具体EV 调度时,倾向于优先调度SOC 较大的EV。
4 基 于W-GAN 与k-means 算 法 的EV 群 体分类方法
传统的EV 群体分类方法基于区域概率模型。考虑到EV 区域之间的流动性与随机性,本文采用了基于W-GAN 与k-means 算法的EV 群体分类方法,GAN 技术强化其原始数据的行为特征,并根据行为特征使用k-means算法进行群体划分,如图2所示。图中不同颜色圆点表示具有不同行为特征的电动汽车,其上箭头表示EV 的流动,连线表示找到具有相同行为特征的EV的联系。
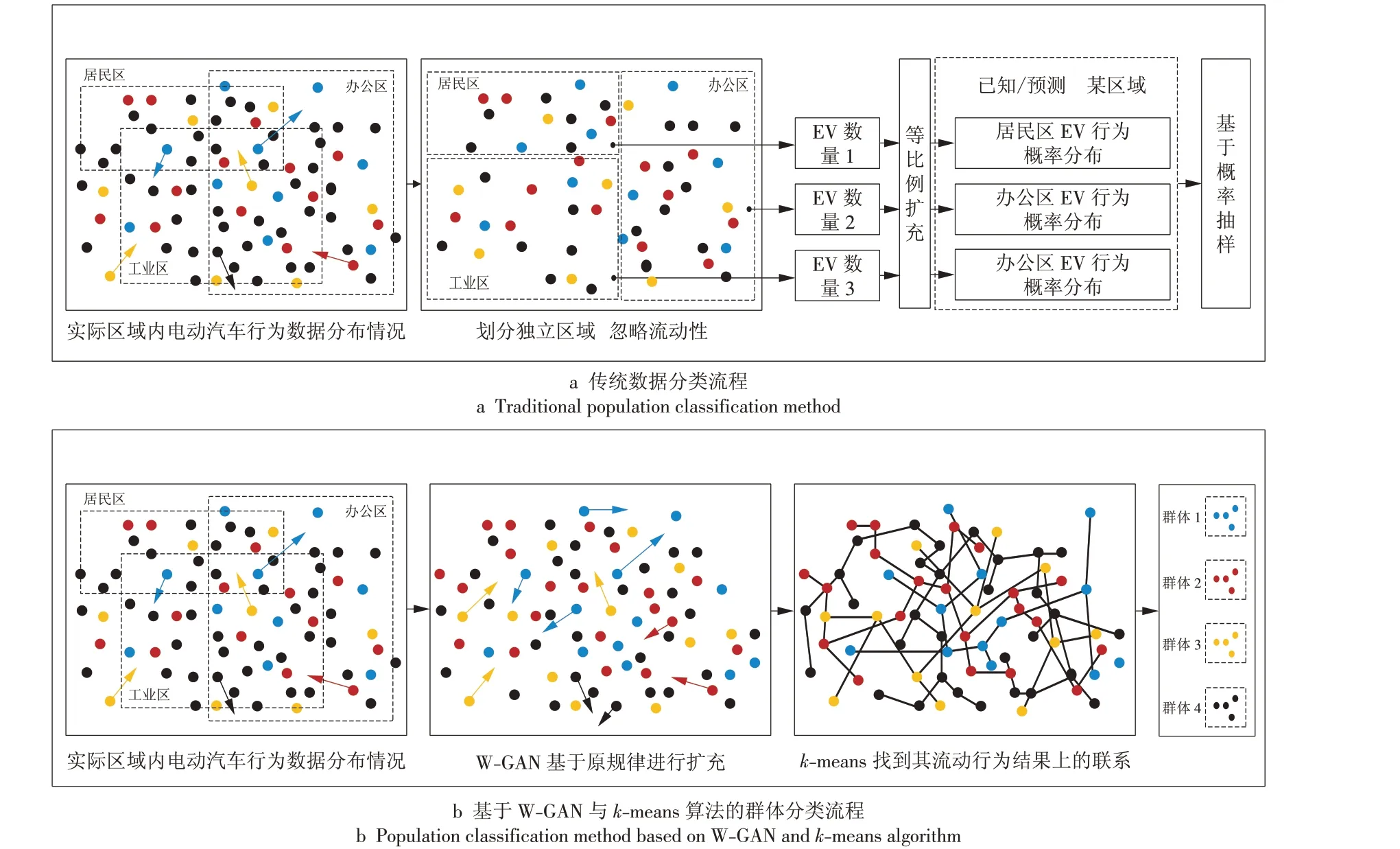
图2 2种算法下的EV行为数据群体分类方法流程对比Fig.2 Comparison between two population classification methods for EV behavior data
GAN 通过生成器与判别器博弈,学习输入数据的特征从而产生具有与输入数据相同特征分布的数据。
生成器损失函数Lz~pz=Ez~pzlg(1-D(G(z)))。判别器给生成器的评分越高,则生成器性能越高,则Lz~pz越小,生成的伪数据分布更符合真实分布。
原始GAN生成器的目标函数为
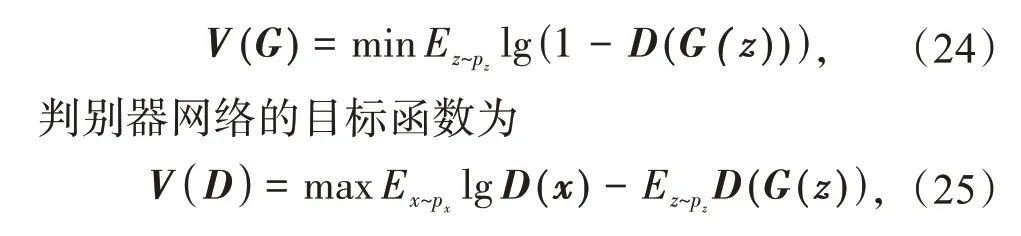
式中:D(x),G(z)分别为真实数据与伪数据,二者输入维度一致,输出维度为1,输入/输出维度是介于0与1 之间的张量,输出越接近1,则表示生成器生成的数据越接近真实数据;D(G(z))代表判别器给生成器的评分;pz为噪声分布;px为真实数据的分布。
综上所述,原始GAN的目标函数为
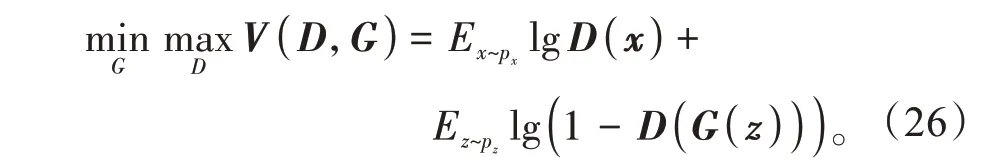
处理原始GAN 的目标函数会导致网络存在梯度消失、训练困难等问题[20],因此,采用Wasserstein距离代替原目标函数,得到
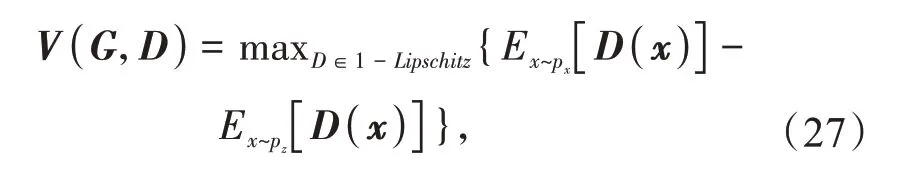
Lipschitz约束为函数f(x)在任意两点之间的连线斜率小于等于K,即
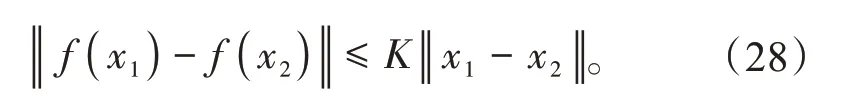
为了进一步提高神经网络的学习能力,以卷积神经网络代替原有的全连接神经网络,最终形成改进的网络W-GAN。
k-means 聚类算法通过计算各元素与随机选取的聚类中心的之间的“距离”,将元素划分到k个聚类中,聚类效果与数据精确程度以及聚类个数k的选取有关[21]。
为获得更好的聚类效果,本文一方面通过WGAN 算法强化数据特征,削弱干扰数据对数据集中的影响;另一方面通过基于畸变程度分析的手肘法(Elbow Method)缩小k值选取范围[22],并通过引入轮廓系数(Silhouette Coefficient)[23]确定合适的k值。结合W-GAN,Elbow Method 与Silhouette Coefficient的k-means聚类过程如图3所示。
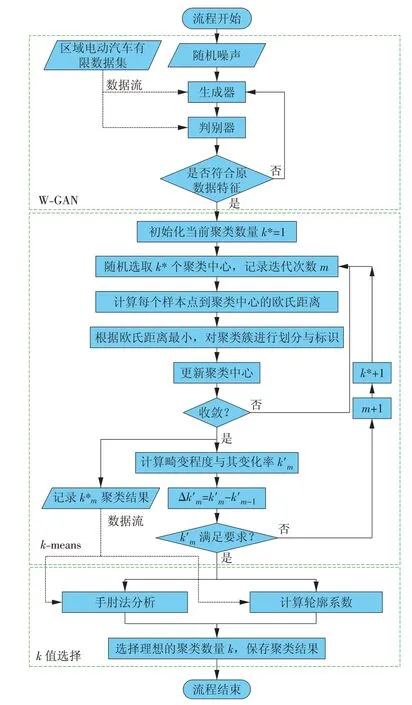
图3 电动汽车群体聚类算法流程Fig.3 Electric vehicle population clustering algorithm flow
轮廓系数
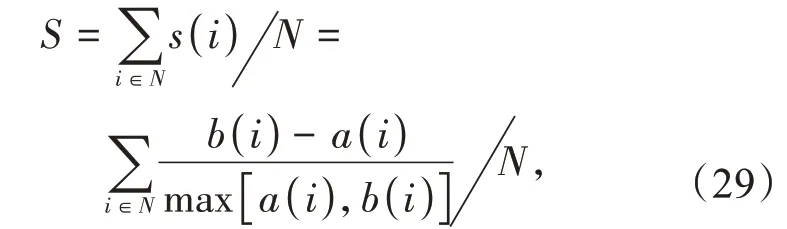
式中:N为总样本数;s(i)为样本i的轮廓系数,s(i)∈[-1,1];a(i)为样本i到同簇其他样本欧式距离的平均值;b(i)为样本i到其他簇所有样本欧氏距离的最小值。s(i)越接近1,则表示样本i越靠近所在簇的聚类中心,对i的聚类越合理;s(i)越接近-1,则表示样本i越靠近其他簇的聚类中心;s(i)=0,表示其位于两簇的交接处,可被分到任意一个簇中。式(29)表明,聚类结果的轮廓系数S∈[-1,1]为每个样本轮廓系数的均值,可度量聚类结果的合理性。
5 算例分析
5.1 参数设置
以某区域典型日负荷为例,对零散EV 充电行为数据(如图4 所示)[24-25]进行处理,提取本文所需参数,并通过W-GAN 数据增强算法扩充为贴近原始分布的1万辆电动汽车充电行为数据。

图4 某区域典型日负荷分布Fig.4 Typical daily load distribution for an area
根据QC/T 841—2010《电动汽车传导式充电接口》中的常规充电要求计算[26],设定该区域EV 充放电功率为恒定7 kW,充放电效率为90%。
算例设定调度策略规划的SOC,E为0.8,SOC,low为0.2,仿真周期为24 h,单位时间间隔为1 h。本文在CPU AMD R7 5800H,16 GB内存的计算机上完成仿真。
5.2 仿真结果
5.2.1 电动汽车群体分类结果
采用W-GAN对原始数据进行扩充,得到1万辆电动汽车充电行为数据,其中电动汽车入/离网时间分布如图5所示。
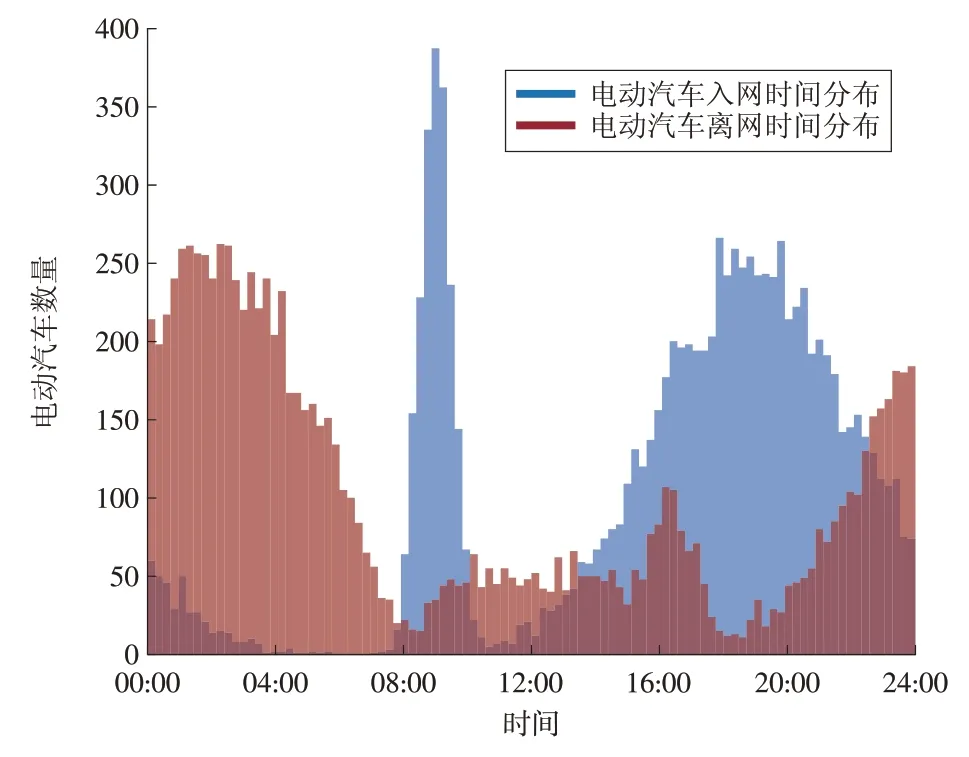
图5 基于W-GAN的区域电动汽车入离网时间分布Fig.5 Distribution of on-grid and off-grid time of electric vehicles by W-GAN
采用Elbow Method 与Silhouette Coefficient 综 合评估,通过基于k-means 聚类算法二次聚合,根据其充电行为参数分布特征将EV 分为4个群体,其聚合效果如图6所示。
从图6 的稳定结果上看,EV 的充电行为数据具有一定的聚集特征,可将其划分入不同的EV 群体中。

图6 电动汽车充电行为参数聚类(截图)Fig.6 Clustering of charging behavior parameters of EVs(screenshot)
5.2.2 算例1仿真结果
算例1 对可调度能力与调度效益2 部分进行了综合可调度潜力评估。不同群体EV 可用于削峰及填谷的负荷如图7所示。
图7显示,不同EV 群体下的汽车在不同时间段具有不同的削峰或填谷能力,处于群体1 与群体2的EV 可用于削峰的容量仅在3 MW 左右,与电网互动能力较差,即可调度能力较差;而群体3 与群体4的EV 可调度容量较群体1 与群体2 均有所提升,说明群体3 与群体4 参与调度后与电网的互动能力较高。
将上述群体分别运用于削峰填谷,实际效果如图8所示。
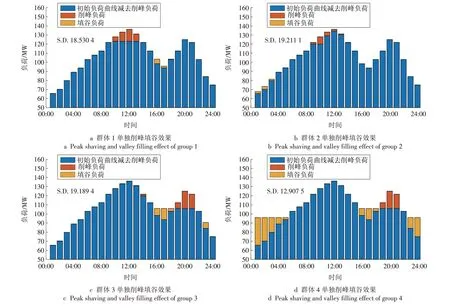
图8 不同电动汽车群体单独削峰填谷效果Fig.8 Peak-shaving effect of different EV groups individually
结合图7—8 可见,虽然群体1 相较于群体3 可调度容量较小,但由于处于群体1的EV 停留时间范围更贴近负荷的峰值,因此利用群体1的EV 进行削峰填谷调度后,剩余负荷需求的标准差仅为18.530 4(基础负荷标准差为20.532 2),小于群体3的19.189 4,削峰填谷效果更好。而群体4 电动汽车不但具有较高可调度容量,停留时间段又处于负荷波动较大位置,因此削峰填谷效果最好,调度后的负荷标准差为12.907 5。算例结果验证了通过可调度能力与调度效益2部分建立综合可调度潜力评估模型的合理性。
5.2.3 算例2仿真结果
算例2对本文所提出的综合可调度潜力评估模型评估结果进行分析验证。运用所提综合评估模型,对不同群体根据其削峰填谷能力以及其与基础负荷峰谷之间的距离关系进行综合评估,各评估指标见表1。
结合图7的各电动汽车群体实际削峰填谷能力以及表1 的评估结果进行分析。该区域的4 个群体中,群体4 可调度容量最高,群体3,1,2 可调度容量依次递减,指标f'a,d评估结果与实际情况相符。
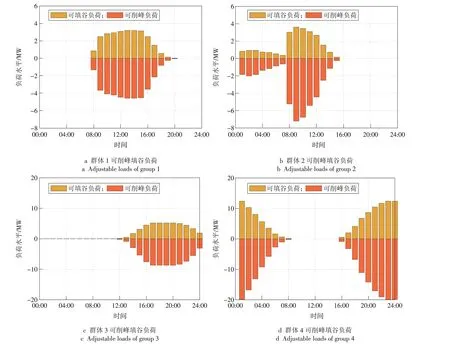
图7 不同电动汽车群体削峰填谷能力Fig.7 Peak-load regulation capacity of different EV groups
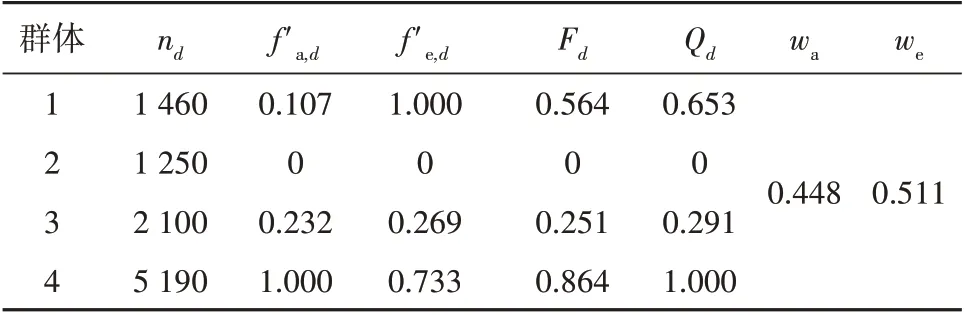
表1 不同电动汽车群体综合可调度潜力评估Table 1 Evaluation table of the comprehensive accessibility potential of different scenarios
指标f'e,d对应各群体EV 停留时间范围与基础负荷峰谷之间距离的综合评估。图7 显示群体1 中电动汽车在09:00—14:00 停留,与10:00—13:00的基础负荷峰值对应较好,同时表1 中群体1 的指标f'e,d最高,表明对其调度效益最高;群体3 和4 中EV 停留时间内均包含基础负荷中不同时长的峰值或谷值,其指标f'e,d也较高;而群体2的EV停留时间段处于基础负荷上升的中间阶段,对其进行调度效益较低,效益评估对应也最低。其对应关系表明,指标f'e,d评估结果与实际情况相符。
根据f'a,d与f'e,d的无序程度使用熵权法确定其权值,计算得到各群体综合可调度潜力评估指数Fd,Fd越大表明对该群体EV进行调度后削峰填谷效果相对越好,应进行优先调度。将表1 中各群体评估结果与图8 各群体实际削峰填谷后的标准差比较,所得调度顺序对应相符。
5.2.4 算例3仿真结果
算例3对采用划分优先调度区与传统集中式调度的EV进行调度效果对比,如图9所示。
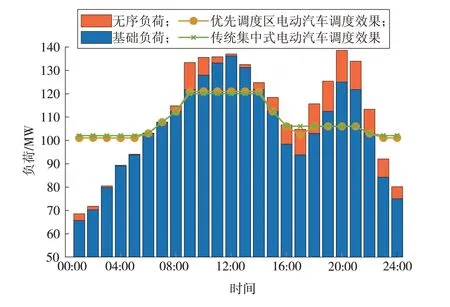
图9 不同电动汽车调度方式下削峰填谷效果Fig.9 The effect of peak shaving and valley filling under different electric vehicle dispatching methods
根据表1 评估结果,基于Fd的归一化指标Qd选择群体1与群体4为优先调度区,群体3为备用调度区,群体2 为不宜调度区。将优先调度区的电动汽车用于削峰填谷,并与传统集中式调度效果进行对比,如图9 所示。对优先调度区的电动汽车下发调度指令,即可使最终负荷曲线贴近传统集中式调度下的理论最优调度曲线。
从标准差角度,仅对优先调度区电动汽车下发调度指令,即可将总负荷的标准差由最初的20.532 2降低到8.049 0,即用66.5%的电动汽车即可完成传统集中式调度效果的94.1%,但相较于传统的集中式调度,减少了33.5%的电动汽车调度数量。
可见对优先调度区电动汽车调度即可用较少的调度量完成较好的调度效果。而加入备用调度区后,调度效果如图10所示。
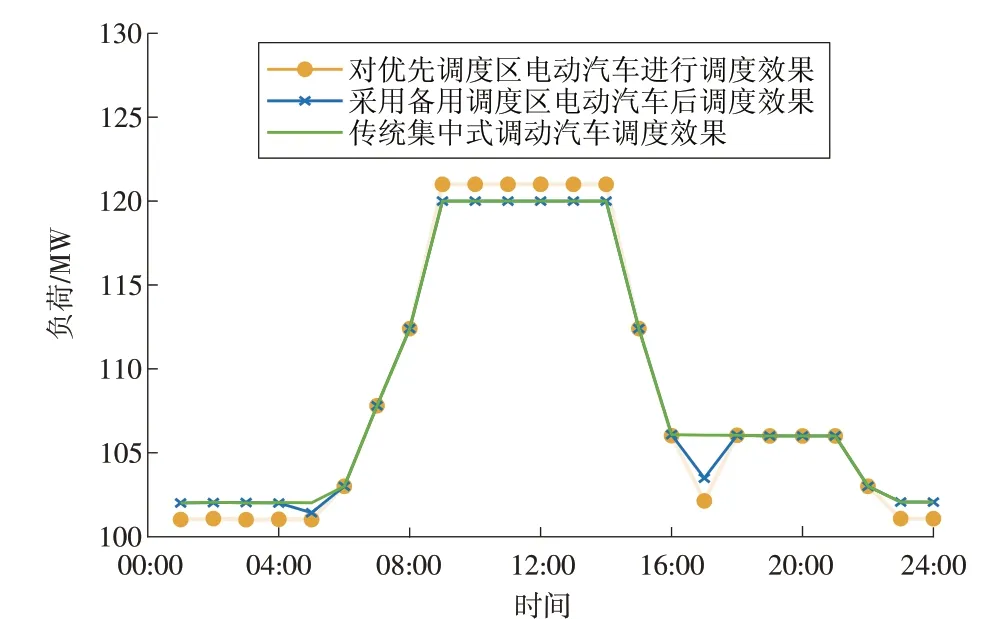
图10 加入备用调度区电动汽车后削峰填谷效果Fig.10 Peak shaving and valley filling effect after adding EV backup dispatch zones
加入备用调度区的电动汽车对削峰填谷的作用效果已经较低,仿真结果表明,对备用调度区内占总EV 数21%的电动汽车进行调度,仅将标准差由8.049 0 降低到7.409 5,完成度提升仅为4.8%,调度价值较低,仅作备用设置。
综上可知,所建综合可调度评估模型具有一定的合理性,且根据评估结果划分优先调度区,可在取得较好调度效果的前提下大大减少电动汽车调度数量。
6 结束语
考虑到当前电动汽车调度中对单个电动汽车调度造成的控制指令下发数量较大的问题,本文首先结合电动汽车侧的调度能力与电网侧的需求紧急程度,提出电动汽车综合可调度潜力评估模型,并根据评估结果筛选具有较高调度价值的电动汽车,划分优先调度区下发调度指令,缓解电网下发的调度指令数量需求。
模型求解过程中考虑电动汽车的流动性以及运算量较大的问题,使用基于W-GAN 数据增强算法以及k-means 聚类算法的群体构建方法,在电动汽车跨区域流动情形下,减少评估模型对电动汽车逐次计算的资源占用。
以削峰填谷为算例分析证明,所提评估模型在满足削峰填谷要求的情况下,可减少所需调度的电动汽车数量,提高电动汽车调度效率,为电动汽车调度提供参考与指导。
