智慧仓储设施选址及评价研究

0 引言

选址是企业进行实际投入运营前的重要一步，选址的决策问题通常会影响到企业的投资收益、运营成本、税收政策优惠、销售渠道、企业竞争力、企业资源利用以及企业的持续发展等多个方面[1]。仓库作为货物的储存中转中心，除了具有保证货物完整性，直接影响物流各功能衔接的紧密性，表现为影响配送速度和配送成本进而影响整个物流的成本与效益。传统的选址仅凭以往经验加上信息的传递不及时容易造成货物供应与需求的不平衡，会造成部分仓库货物大量沉积，相反有的仓库经常断货等。目前在智慧物流的背景下，用累积的用户与商家数据如不同地区的物流量大小进行需求预测，结合人工智能相关的规划技术，给模型赋予针对性的约束条件（顾客、生产商和供应商地理位置，土地建筑成本、税收、运输成本等），最终再由计算机自动进行优化和学习[2]。

国内对仓储设施选址问题有着深入的研究，程珩在《物流配送中心选址的重心法探讨》中指出仓储中心选址的重点即追求成本的最小化，包括建设运营成本、运输成本等[3]；王朋、王晓强等学者从服务业、家电零售业等方面对仓储的选址问题进行了探讨，表明仓储的选址问题是企业发展的关键问题[4]；张倩在《智慧农产品仓储选址及追溯研究》中构建了农产品仓储选址的数学模型和地理模型，设计了农产品物流配送的实用方案[5]；王佳在《基于AHP的长沙农产品物流园选址评估》中通过单因素评分评估备选地建设农产品物流园区的可行性[6]；楚哲宇在解决生鲜仓储选址问题中应用了0～1规划及麻雀搜索算法[7]；赵俊逸、姜岩在《基于AHP的施工方项目部仓储物流园区选址评估》中使用层次分析法对仓储园区进行评估，为施工单位项目部选址提供依据，但均未与涉及结合实际地址对比分析[8]。本文主要研究智慧仓储选址的理论方法及方法的实际应用，之后在总结前人研究成果的基础上，结合实际情况对案例中公司的智慧仓储选址进行深入研究。

选址方法有很多，通过具体数据建立数学模型求解归为定量分析，计算复杂但精确性高，缺点是对一些不能数量化的指标无法操作，定量分析方法可以求出较为准确可靠的解，主要有重心法[9-11]、混合0～1整数规划方法[12]、乘权Voronoi图[13]等。定性分析结合较为全面的各影响因素与前人经验加以分析，简单直观，比定量分析具有一定优势，但缺点是结果具有主观性，误差较大，一般不会单独使用此方法。本文采用定量分析方法中的重心法构建模型，并用定性分析中的层次分析法对求解的结果进行评价。

1 智慧仓储选址模型建立

1.1 问题描述

综合考虑各方面因素能为选址提供充足依据，仓储的地址对商品流转费用和流通速度产生直接的影响，并关系到企业对客户的服务质量和服务水平，最终影响企业的销售量和利润，一旦选择不当将对企业产生很多不良后果，且很难改变[14]。成本分析主要体现在承包土地使用权费用、人工成本、水电成本及其他手续费。仓储用地需要较大的场地，目前所租用的场地面积较小，技术设施不够齐全，经常使用的叉车、加包机、液压车数量较少，不能满足A公司建设智慧物流园及仓储系统的使用运行，故必须自己建设仓储用地而不是租用。

对仓储选址采用定量分析法，最常使用的理念包括成本最低、效益最高以及投入产出比三种，先设定若干变量和参数，根据实际情况和需要设置范围或限制条件，然后以数学公式的形式建立起数学模型[15]。重心法理念是将需求地点与资源地点之间的运输距离及需求量放在同一个平面，给每个需求点确定平面坐标，根据需求量、距离、单位运量费用得出运费函数表达式，最后使运费最小进行微分求解，得到最佳位置坐标即可。利用物流系统重心的方法来确定物流网点的位置[16]。如图1所示。

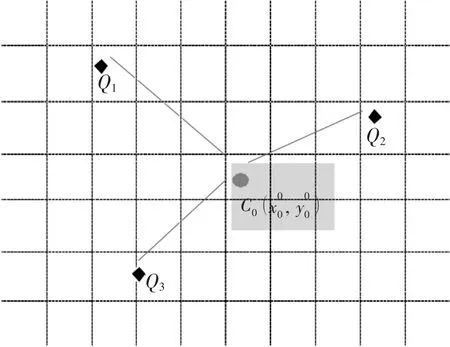
图1 重心法示意图

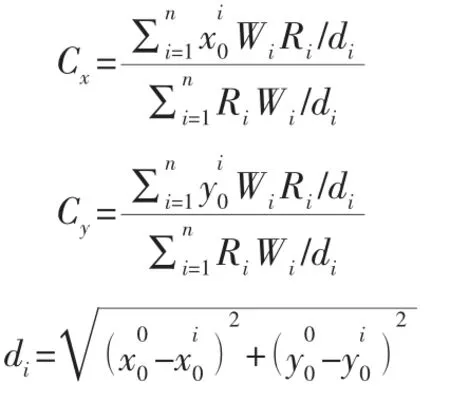
运输总费用（运输费率乘以运输量再乘距离）用H0表示，则：

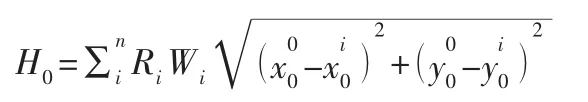
选址的目标是使运输总成本最少，则重心选址模型可以表示为：

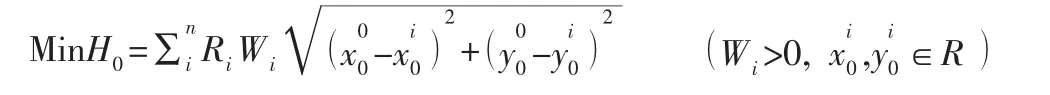
1.2 选址原理与原则

（1）协调性原则：即相互协调，将企业现有的物流网络系统看成一个整体，其中仓储用地选址的基础设施、设备维护、技术手段等要相互协调[17]。（2）经济性原则：即要保证同等约束条件下建设费用、物流费用最小化。如在选择市区或郊区时不仅考虑土地费用，还需考虑运输费用。（3）战略性原则：一要考虑整体，二要考虑长远。即眼光要放长远，不能只局限于局部的利益，要用长远的眼光进行决策。（4）可持续发展原则：就是在保护环境的基础上，结合公司的长远利益，维护生态环境，促进一体化发展。

2 结合实例的选址方案求解

由于A公司的主要供应商位于省外且相对分散，收集的资料不够全面，所以本文研究的仓储中心选址主要根据需求点的情况，先把A公司现有的三个主要需求方作为建模的需求点，围绕这三个需求点选择一个地址，建立一个智慧仓储中心。目标是依靠仓储中心与需求点关系所建立的智慧仓储中心总费用最低。本文将通过重心法模型做具体的计算，且A公司主要供应商位置已知。

综合以上分析可知：A公司在市区的服务网络可归纳为单设施选址理论。理论结构图如图2所示：

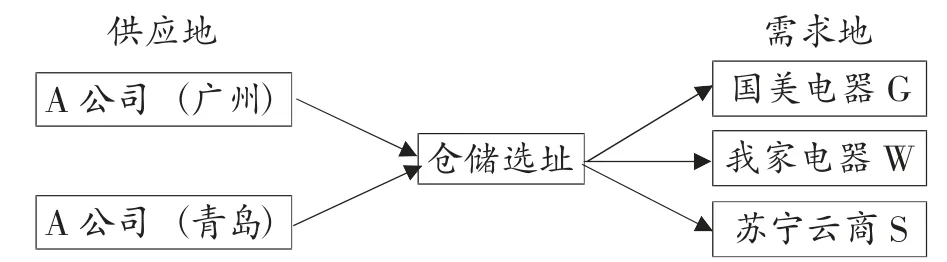
图2 理论结构图

2.1 模型假设

（1）需求地的需求量和位置为已知；

（2）拟建仓储中心的容量能够满足客户的需要；

（3）运输费用与运输量、运输距离的关系是线性的；

（4）仓储中心与需求点间的单位运输费用为已知。

2.2 模型构建

由前文相关理论结合实例具体情况，以最小化成本为目标的函数模型如下：

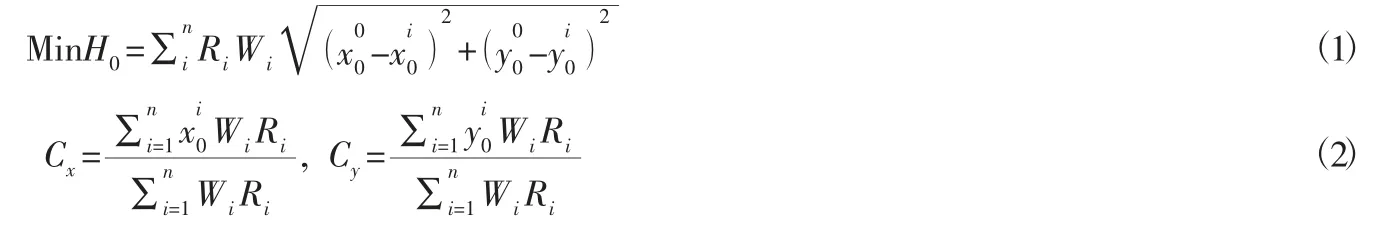
根据式（1）、式（2）并结合相关资料，在模型实例数据基础上计算初始仓储中心坐标及初始运输成本如表1所示，其中运输费率Ri（元/公里）取0.5：

表1 计算运输成本

多次迭代可得出需求点与仓储中心新坐标的距离di以及新的运输成本WiRidi，若迭代之后选址位置的运输成本小于初始的运输成本则继续迭代，最终迭代结果如表2所示：

表2 迭代最终结果

此时，第八次迭代的运输成本=4 806.3401＞第七次迭代的运输成本=4 806.1241，可知若继续迭代成本增加，故停止迭代，得出A公司智慧仓储的最佳位置坐标为(5.57,8.844)，此时能保证到3个需求地点的总运费最省。

3 选址的评价及相关建议

3.1 评价理论—采用层次分析法

目前A公司智慧仓储的选址地点与本文采用重心法算出的坐标地址存在一定误差，因为在实际进行选址建库的时候，会综合地价、运价、流量、政策及不可抗因素（如模型所求出仓储的地址并无可用土地等）。为使差距的合理性具有一定说服力，采用层次分析法以及前文提到的A公司仓储选址影响因素分析，对仓储选址指标进行评价。

建立选址指标层次结构模型如图3所示。

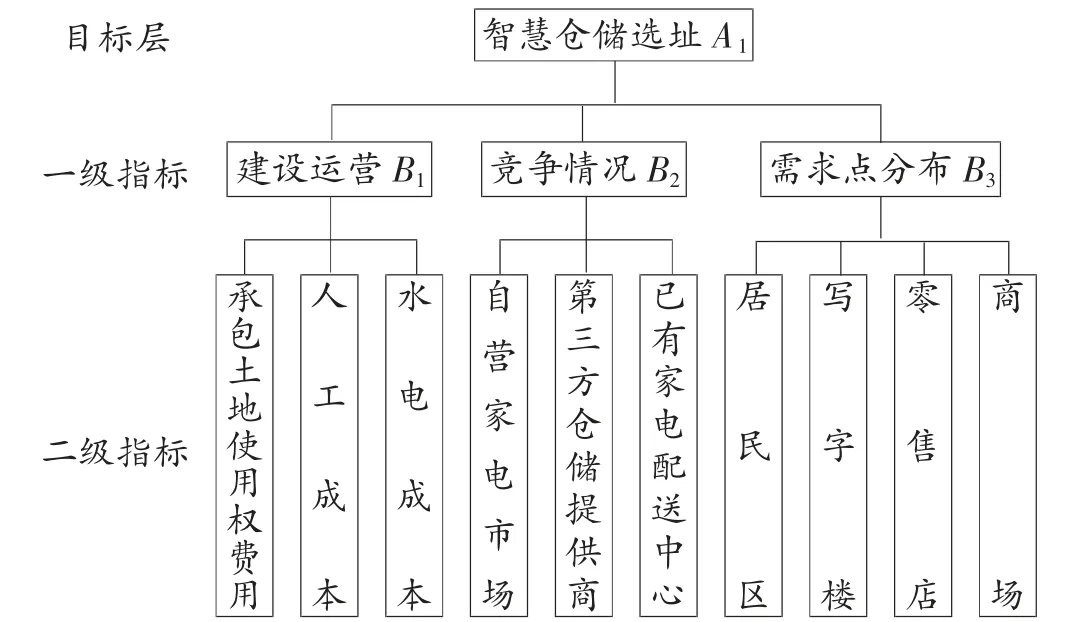
图3 选址指标层次结构模型

通过专家打分以及实地调查资料得出各指标判断矩阵，经过排序做出决策。矩阵的λmax与一致性检验如表3所示，CR＜0.1，层次结构模型对应各指标矩阵均通过一致性检验。

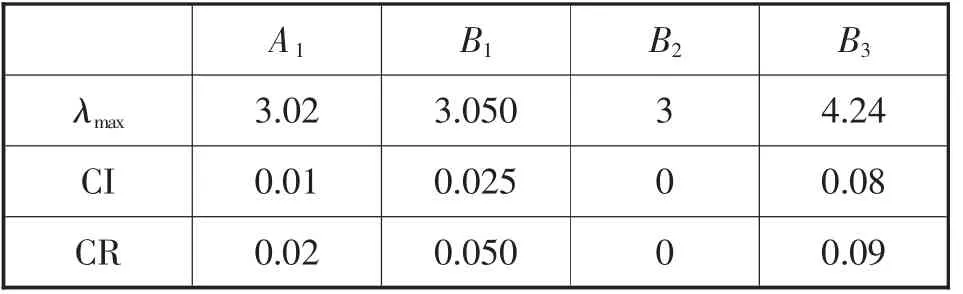
表3 权重相关系数表

通过计算各影响要素的相对权重，并进行一致性检验，得到影响因素总排序，权重大小由轻到重分别是建设运营成本、需求点、竞争因素。故在对比目前A公司智慧仓储的选址地点与本文采用重心法所求地址时，优先考虑成本因素，在搜集目前当地各区域市场价后，得出A公司目前在高新北区果业科技园附近的选址是合理的。

3.2 A公司智慧仓储已选址地点的评价

目前公司在建的智慧仓储物流园位于该市高新北区公交车场附近，总占地面积为73 726.32平方米，国有建设土地使用权出让年期为商业40年，出让价款为4 930万元。

3.2.1 同地址范围内分析

就A公司来讲，所选的智慧仓储建址地点在开发区北边，周围并没有已建成或待建的仓储中心，且建址地点所属国际合作产业园，附近还有科研大厦、升晟股份有限公司、蓝天丽苑住宅区等潜在合作伙伴或客户，它们已经在该地产生了固定人流量、客流量等，对A公司智慧仓储物流园建成带来一定帮助。

3.2.2 交通运输环境分析

A公司的选址位置紧接乌阜城际铁路以及乌奎北联络线，且在沙河沿火车站点附近，方便从省外运输家电等货物，交通便利，具有地域优势。除此之外，A公司智慧仓储物流园正好建筑在当地轨道交通6号线上，且位于吐乌大高速与乌奎高速交汇角，为给国美、我家、苏宁云商等需求点派送货物提供极大便利。

3.2.3 政策因素分析

A公司注册地点就在高新技术开发区，熟悉市区的相关政策规定，再根据高新区北边区域土地的使用费用较低，且位于城镇边缘，为选择到目前所建地址加分。且选址地点在高新区国际产业园内，享受国家及自治区优惠政策。除此以外，A公司的选址地点离市中心较远，一定程度上减轻了交通压力、降低了对生活环境的影响。

4 结 论

通过对智慧仓储选址的研究，了解智慧仓储的基础知识，将选址的重心法应用于现实生活中，综合考虑各方因素灵活的处理问题。在研究过程中框架清晰，内容丰富，构建了合理的数学模型，并对实例进行了求解分析，结构完整。在研究的过程中，由于学习经验不够丰富，相应的研究技术掌握不完善，在对课题的数学模型构建中只考虑了同地址下的竞争关系、供需点、运营成本、政策法规等影响选址的因素，未涉及供需波动、环境变化等因素，与现实生活中的实际运送情况不够贴合。

在未来的研究中，将学习更多的技能，不断丰富数学模型的约束，使其更加贴近现实的选址过程，将更多因素考虑入内，使选址结果更具有可行性，运用更加复杂的算法来求解本文的路径优化问题，以更迅速地得到更加优良的解。此外，在运用层次分析法上，尤其是各个因素的打分标准以及标准的采样，存在一定难度，因此，需要寻求更加客观、理性的决策方法，这也是后续有待学习的地方。