基于Shapley值组合模型的我国快递业务量预测

赵桂红，孙 曜

（1.中国民航大学 经济与管理学院，天津 300300；2.中国民航大学 交通科学与工程学院，天津 300300）

0 引言

中国目前已经成为全球最大的网络零售市场，这主要得益于我国线上零售业及快递行业的快速发展。过去十年我国快递业务量已经由2012年的56.85亿件增长到2021年的1 083亿件，快递行业收入也从2012年的1 055亿元爆发式增长至2021年的10 332亿元。快递业已经成为现代服务业高效运行的重要保障，也成为社会经济发展的重要支撑。《“十四五”邮政业发展规划》中提出邮政业发展仍然处于重要战略机遇期，到2025年要努力实现我国邮政业在规模实力、基础网络等方面的新跃升，这也对我国快递行业提出了更高层次的挑战[1]。为实现高质量发展目标，不仅需要快递企业提高服务能力，更需要政府及邮政管理部门营造良好的外部环境，精准有效的把握快递行业发展动态及趋势，推动快递业迈向高质量发展阶段。

快递业务量是衡量一个国家或地区邮政快递规模、评价快递行业发展的重要指标。一般情况下，快递业务量较大时说明快递业发展水平较高，快递业务量增长较快时则说明快递行业发展迅速，此时快递企业需要调整策略以满足增长的快递需求。科学准确的快递业务量预测对快递企业优化人力设备资源配置、提高运输效率具有重要作用，对邮政业乃至城市经济高质量发展均有重要意义，同时也可以为政府规划快递业发展方向、制定发展战略提供参考，助力快递行业更快更好的实现高质量发展的目标。

目前，国内外学者关于如何科学合理预测快递业务量展开了众多研究，所运用的方法主要包括灰色预测法[2]、多元回归模型法[3]、BP神经网络算法[4]、深度学习法[5]等。这些预测方法在本质上都是基于原始数据建立拟合模型进行预测，应用均有一定的局限性。如灰色预测法虽然能在缺少数据时有很好的预测结果，但该模型在原始数据离散程度过大时预测精度会大大降低；回归模型法需要在快递业务量数据变动平稳、趋势较为明显的情况下才会使结果具有很高的精准度等。电子商务的兴起及“四通一达”的成立带动了我国快递行业的快速发展，我国快递业务量呈现出极速增长的特征，2012年以来我国快递业务量年增长率最高达到了61.5%，因单一预测方法存在局限性，会导致预测精准度不够高。Bates和Granger[6]提出了组合预测模型，即将两种或两种以上不同的预测方法进行组合建模，可以充分发挥单一预测模型优势，同时减少由参数错误或模型错误带来的预测误差[7]，以其较高水准的预测精度受到了国内外众多学者的青睐。在组合模型预测研究中，重点是选择合适的组合方式，即选择组合时的权重分配方法。Shapley值法常用于研究合作中的利润分配问题，其分配结果的公平性得到了高度认可。在组合预测权重分配中，可以将总误差视为收益，分配结果则为各方法的所占权重。

结合国内外研究学者对组合预测模型的研究成果，本文选取2012—2021年我国快递业务周转量数据，先分别构建灰色GM（1,1）预测模型、多项式趋势外推预测模型及指数平滑预测模型，再将三种模型采用Shapley值法进行组合，并比较分析三个单一模型与组合模型的预测效果，最后采用预测精准度更高的预测方法对2022—2025年我国快递业务量进行预测，分析快递业务量的变化趋势与波动规律，为我国快递业务量的预测提供新方法与思路。

1 三种单一预测方法对我国快递业务量的预测

1.1 样本数据说明

本文采用灰色GM(1,1)预测、多项式趋势类推预测、指数平滑法的组合预测方法进行预测，选取2012—2021年我国快递业务量为样本。原始数据来源于《中国统计年鉴2021》，具体数据见表1。

表1 2012-2021年我国快递业务量统计数据单位：万件

1.2 基于灰色GM（1,1）的我国快递业务量预测

灰色GM（1,1）模型可以通过对原始数据进行累加处理，削弱原始数据的随机性，生成有较强规律性的数据序列，进而建立微分方程模型并求解，以此探究系统变动的规律并对事物未来发展趋势进行预测。本模型适用于快递业务量的预测，其模型步骤如下：

将各年度的快递业务量构成原始数据序列x(0)：

对各年度快递业务量原始数据进行一次累加，生成1-AGO序列

其中x(1)：

新序列可以增加快递业务量原始数据的规律性，然后构建累加矩阵B与常数向量Yn：

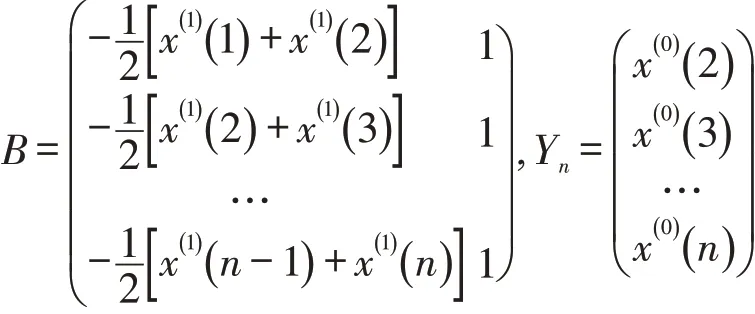
对新序列建立微分方程：

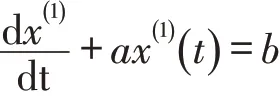
其中a为发展灰数，b为内生控制系数。

然后计算参数:

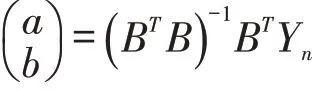
代入得预测模型为：

最后还原为预测值。

对我国2012—2021年快递业务量进行灰色GM(1,1)模型构建，通过级比检验判断数据序列进行建模是否适用。当原始快递业务量数据序列的级比在可容纳区间内时，则表明原始数据为光滑序列，此时可以采用灰色模型进行预测，而原始数据样本并没有通过级比检验，因此需要进行平移转换，在原始数据基础上加上平移转换量10 830 000，最终平移转换后的数据级比检验均在标准范围区间[0.834,1.199]内，此时可以选用灰色GM(1,1)模型进行预测。

采用SPSS 25.0软件对平移转换后的快递业务量进行分析，可得a=-0.265 9、b=102 603 9.133 5。将其代入到模型公式中，得到灰色GM(1,1)模型预测结果及误差情况见表2。

表2 基于灰色GM(1,1)我国快递业务量预测结果

选用平均相对误差作为我国快递业务量灰色预测模型精度的检验标准，采用灰色预测模型时的平均相对误差为10.44%，意味着模型精度等级较好，但根据表2中预测结果可以看出，2013—2015年的误差较大，导致整体的相对平均误差较高。

1.3 基于多项式趋势外推法的我国快递业务量的预测

多项式趋势外推法是以已知的统计数据为基础，构建多项式模型，推断未来发展趋势，实现对未来数据精准预测的一种方法，适用于经济、科技和社会发展的预测。当快递业务量随时间变化呈现出上升的趋势，且能找到一条能反映此变化的多项式函数曲线时，可以采取此方法进行预测。其表达式如下：

一次线性预测模型:

二次抛物线预测模型:

三次抛物线预测模型:

其中，yt为预测值，b0为常数项，b1、b2、b3为时间t的系数。由此类推多项式趋势外推模型的一般形式为：

采用SPSS 25.0软件对2012—2021年快递业务量进行回归分析，以时间t为自变量，快递业务量y为因变量建立一元多项式方程进行拟合。经各类多项式拟合后发现一元二次曲线方程拟合度最好，此时R2=0.996，表明模型适合快递业务量的预测，拟合方程为：y=447 622 717 696-445 041 237.250*t+110 618.833*t2

其预测值与误差情况见表3。

表3 基于多项式趋势外推模型的我国快递业务量预测结果

由表3可以看出，二次多项式预测模型的结果与实际值之间的误差较小，满足精度要求，但是二次曲线函数在对初始年份的预测中误差较大，且后期对快递业务量的预测值普遍偏大，因此只适用于短期预测。

1.4 基于指数平滑法的我国快递业务量预测

指数平滑法是所有预测方法中最常用的方法，适用于对快递业务量的预测。指数平滑法可以分为一次指数平滑、二次指数平滑和三次指数平滑（Holt-Winters）方法，其基本公式是：

其中St为第t期的预测值，yt为第t期的实际值，St-1为第t-1期的预测值，α为平滑常数，取值范围为[0,1]。

一次、二次、三次指数平滑方法的使用可以由时间序列有无明显的趋势变化进行选择，一次指数平滑适用于时间序列无明显的变化趋势；二次指数平滑适用于具有线性变化趋势的时间序列，是对一次平滑的再平滑；三次指数平滑适用于趋势线性且周期稳定的场景。

本文采用SPSS 25.0软件对我国快递业务量进行预测，改变不同的平滑系数α来找出最佳平滑类型，通过对输入不同α所得到的预测结果进行比选，发现α取值为0.8时为最优，平滑类型为三次指数平滑，模型预测结果见表4。

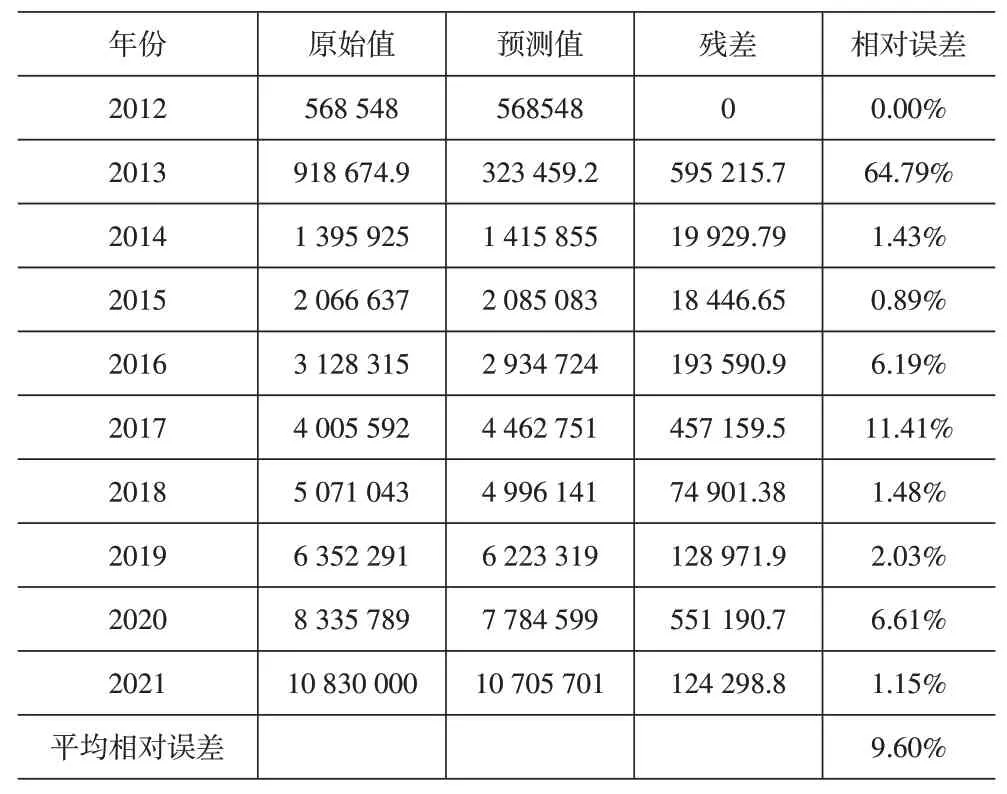
表4 基于指数平滑法的我国快递业务量预测结果

经测算，三次指数平滑法预测结果中的平均相对误差为9.60%，拟合效果较好，但精度相比二次曲线较弱，且在2013年预测相对误差较大。

2 基于Shapley值法的我国快递业务量组合预测

2.1 Shapley值法基本原理

组合预测基于两种及两种以上的单一预测模型，其计算公式可以表示为：

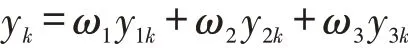
其中，yk为组合后的预测值，ω1、ω2、ω3分别为灰色GM（1,1）预测模型、多项式回归预测模型与指数平滑法预测模型在组合预测中所占权重，且ω1+ω2+ω3=1，y1k、y2k、y3k分别为灰色GM（1,1）预测值、多项式趋势外推模型预测值、指数平滑模型预测值，k为时间序列。其中权重分配即ω1、ω2、ω3的取值是组合预测中最为重要的一环，本文通过Shapley值法来对各项预测模型权重进行合理分配，以达成对快递业务量精准预测的目标。

首先假设有N种单一预测方法，记Ag={1,2,…,n}。s、v为集合Ag中的子集，E(s)、E(v)为各组合的误差，且有E(s)+E(v)≥E(s⋃v),令yi为第i种预测方法最终分配误差，且yi≤E(i)，则n种预测方法组合预测后的总误差E(n)会在这n种预测方法中分摊，即，假设i种预测方法的相对误差均值为Ei，组合预测的总误差为E，则有：

其中|eij|为第i种预测方法对样本j的相对误差值，m为样本数量。

则按照Shapley值误差分配公式为：

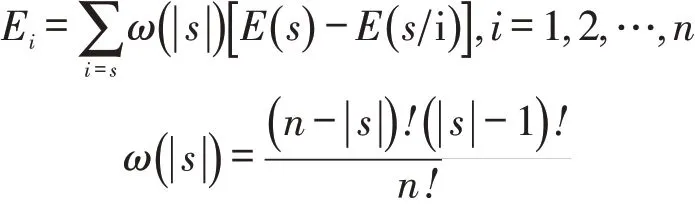
其中ω(|s|)为单预测方法i的边际贡献值；|s|为子集s中单预测方法的个数；E(si)为子集s中除去i后的绝对误差值。

则第i种预测方法在组合预测中的权重公式为：

然后将得出的ωi值代入组合预测模型公式中即可求得基于Shapley值的组合预测值。

2.2 基于Shapley值法的我国快递业务量组合预测实现

根据上文对我国快递业务量的三种预测结果，可以得到总的平均相对误差为E=(10.44+6.10+9.60/3=)8.71。按照Shapley值法，记所用的三种预测模型集合为Ag={1,2,3}，则可以得到组合模型所有子集误差分摊结果，见表5。

表5 误差分摊结果

按照2.1小节的方法计算，可以得出三种方法的Shapley值为：E1=4.20，E2=3.57，E3=0.95。此时E1+E2+E3=E=8.71，即三种预测方法分摊的误差之和等于总误差，然后计算三种预测方法在组合预测中的权重ω1=25.90%，ω2=29.53%，ω3=44.57%。根据所计算的权重，则组合预测模型为：yk=0.259y1k+0.295 3y2k+0.445 7y3k。

可以得到组合预测结果见表6。

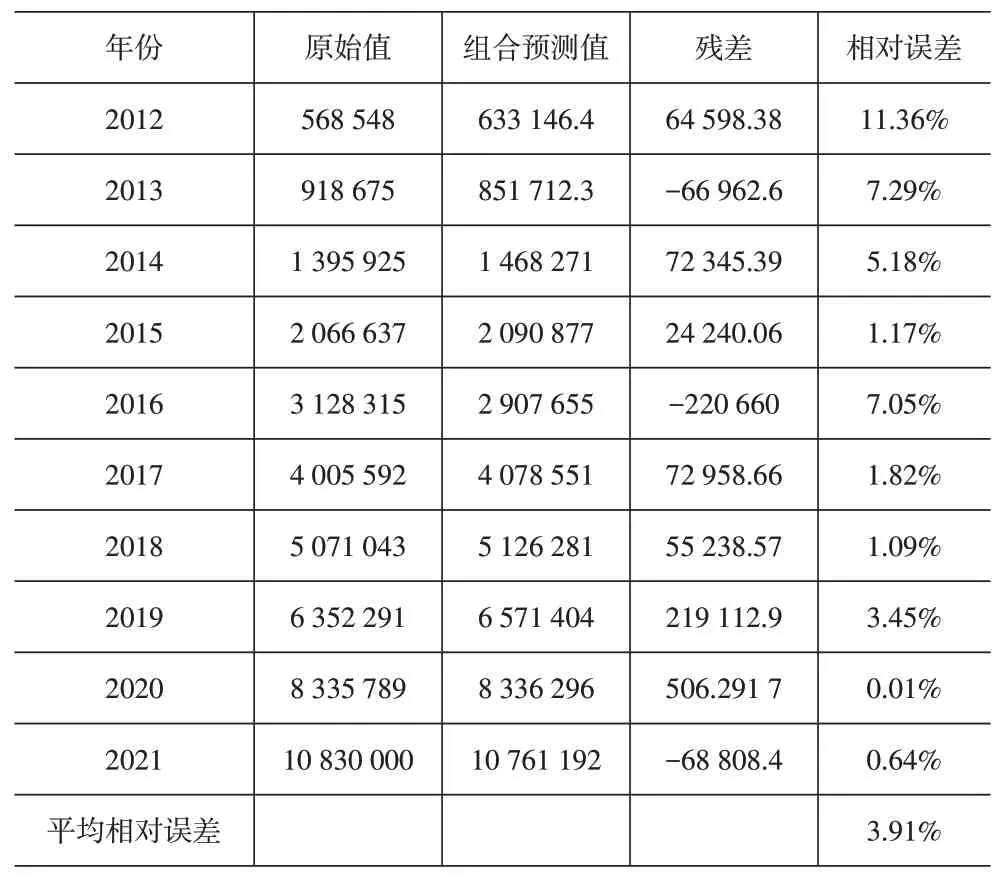
表6 2012-2021年基于Shapley值的我国快递业务量组合预测结果

根据表6可知，基于Shapley值法计算出的各年份预测残差较小，平均相对误差值仅为3.91%，也就是说，与单一预测模型相比，采用Shapley方法对我国快递业务量进行组合预测精度更高。

2.3 “十四五”期间我国快递业务量组合预测

为了对2022—2025年我国快递业务量进行综合预测，首先采用三种单一预测方法进行分年度预测，再根据基于Shapley值法的组合预测模型得出组合预测值，见表7。

表7 2022-2025年我国快递业务量预测结果

由表7的组合预测值可以看出我国快递业务量在“十四五”期间将持续增长，未来几年快递行业将维持高速增长态势。

3 结语

（1）2012-2021年我国快递业务量总体呈上升趋势，且增长速度较快。根据快递业务量原始数据建立了灰色GM(1,1)模型、多项式趋势外推模型和指数平滑模型三种传统单一预测模型，其中灰色GM（1,1）预测模型对初始年份的预测误差较小，但对2013—2015年的误差较大，导致总体的平均相对误差较大；多项式趋势外推模型平均相对误差较小，拟合曲线也比较平稳，但对后期快递业务量的预测值普遍偏大，且只适用于短期预测；指数平滑预测模型预测精度较高，但对初始年份的预测结果误差较大。

（2）本文建立了基于Shapley值的组合预测模型，通过对2012—2021年快递业务量进行组合预测实证分析，证明该组合预测模型可以提高预测精度，为我国快递业务量的预测提供一种有效的方法，有利于决策者准确了解快递业发展趋势，为制定邮政业发展规划提供依据。

（3）本研究有一些不足之处：如组合预测模型中多项式趋势外推方法仅适用于快递业务量的短期预测，在中长期预测时会出现预测值较大的情况；快递业务量会受到多种因素的影响等。未来对快递业务量预测研究中应对这些问题进行优化，以求得更准确、更全面的预测结果。