非对称翼型叶片水力不平衡力的非线性动力学模型及计算分析
2022-12-26向文平黄社华庄克云
向文平,黄社华,庄克云
(1.国能大渡河瀑布沟水力发电总厂,四川汉源 625300;2.武汉大学水利水电学院,湖北武汉 430072)
0 引言
近年来,随着制造业和能源工业的快速发展,水电站向着大容量的方向发展[1],例如2015 年底,水电站装机容量已经达到320.03 GW。但是这些变化将增加水轮发电机组轴系统因水力、机械和电气因素引起的不稳定振动[2-12],这不仅影响了机组正常运行,有的还危及到机组的安全。而且水轮发电机组轴系统在运行过程中,机械、水力和电气因素相互作用。例如,当水流作用于水轮发电机组旋转部分时,会造成发电机转子与定子间的气隙不对称,从而产生磁力,加剧振动。并且,当旋转部件运动状态变化时,也会影响水轮机流场和发电机磁场。因此,为保证水电站的安全稳定运行,对不稳定因素下的水轮发电机组进行非线性动力特性研究是十分必要的。
长期以来,为了研究机械和电气不稳定因素的影响,学者们提出了大量的非线性数学模型[13-18]。一方面,关于机械不稳定因素,Yan等[13]将分数阶导数引入水轮发电机机组,研究了多故障下弯扭耦合发电机转子轴系统的动力学行为。Huang等[14]建立了不对中和碰摩故障下,转子系统的动力学模型,并采用数值积分法对系统的动力学行为进行了分析。Ma等[15]系统地研究了具有平行不对中和角度不对中的悬架转子系统在起降过程中的油膜失稳规律。另一方面,关于电气不稳定因素,Perers等[16]报道了对静态偏心量为20%的水轮发电机的不平衡磁拉力的饱和效应的研究,并采用有限元法和一个简单的解析模型并行计算了各种空载电压和负载下的磁拉力。基于Jeffcott 转子模型,Xiang等[17]分析了永磁同步电机转子系统的刚度特性,研究了不平衡磁拉力影响下的非线性动态行为。Zarko等[18]利用有限元方法计算了凸极同步发电机转子轴在有磁场存在下的偏心运动所产生的不平衡磁力。
水力不平衡是引起水轮发电机组振动的一个复杂而不可预测的因素,其机理是流动沿圆周分布不均匀。可能的原因包括叶片流道不一致、叶片型线不一致、叶尖间隙不一致和叶片接力行程不一致[5]。特别是对于叶片流道不一致来说,主要是由于叶片出口安装角、接力行程和导叶开度不一致造成的。目前为止,虽然对水力不平衡有了一些研究,但主要集中在水力不平衡故障的监测与诊断方面[19-21]。这种方法不能很好地满足水电机组的经济和安全需求。因此,为了研究水力不平衡对水电机组非线性动态特性的影响,本文以非对称翼型NACA2415 为研究对象,在雷诺数为0.5×105到3.5×105的范围内,对NACA2415 翼型非恒定绕流进行CFD 数值模拟,并根据儒可夫斯基定理,建立适用于非对称翼型水力不平衡力的非线性动力学数学模型。进而根据拉格朗日方程建立水机电耦合故障下水轮发电机组非线性动力学数学模型。然后通过MATLAB 对该模型进行计算分析,研究不同雷诺数下水轮发电机组随叶片出口安装角偏差变化的动力学特征。
1 翼型NACA2415非恒定绕流
1.1 计算条件和网格划分
模型建立在C 型的计算域中,计算域的左边界距翼型尖端9c(c为翼型的特征长度),右边界与翼型尾端相差14c,上下边界到弦线各差10c。计算区域采用不同尺寸的四边形结构化网格进行划分,如图1所示。

图1 翼型NACA2415计算网格区域Fig.1 Calculation grid region of the NACA2415 asymmetric airfoil blade
本文湍流模型采用Spalart-Allmaras 模型,边界条件为为压力远场边界条件,离散方法为有限体积法,压力和速度耦合采用SIMPLEC 算法;非定常计算时间步长取0.001 s,最大迭代为20次,迭代步数为2 000 步。
1.2 升阻力特性分析
升力是流体流经翼型表面时翼型受到的垂直于流动方向的作用力,阻力则是翼型受到的与流向相反的作用力。为便于分析,基于无量纲的升力系数(CL),阻力系数(CD)进行讨论,其表达式为:

式中:L为翼型升力;D为翼型阻力;ρ为介质密度;V∞为自由来流速度;c为特征尺度,取为翼型弦长。
图2 给出了雷诺数为3.5×105时,升、阻力系数仿真数据与实验数据[22]的对比。

图2 升、阻力系数仿真值与实验值[22]对比Fig.2 Comparison of lift and drag coefficients between the numerical calculation and experiment data[22]
由图2可以看出,在研究攻角范围内,基于S-A湍流模型所得到的升阻力值随攻角的变化曲线与实测值变化曲线基本一致,仅在临界失速角附近误差较大,说明本文采用S-A 湍流模型开展翼型非定常绕流研究是准确可靠的。
基于此,通过MATLAB 进行拟合,得到升力系数CL和升阻比λ近似计算公式如下:

改变马赫数和来流速度,使雷诺数相应变化为2.2×105和0.5×105,通过MATLAB 拟合得到的升力系数CL和阻力与升力比λ近似计算公式如下:
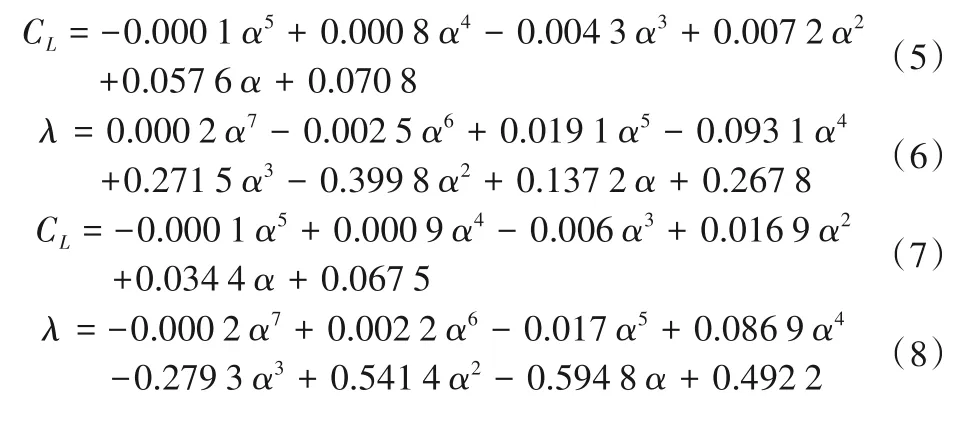
2 水力不平衡力非线性动力学数学模型
2.1 单个叶片受力分析
将转轮内水流绝对速度V沿叶片方向和转轮圆周方向进行分解,分别定义为相对速度W和圆周速度U。对于单个叶片,由儒可夫斯基定理得叶片的径向力如下[21]:

式中:CL为转轮叶片升力系数;F为水轮机叶栅中叶片最大投影面积;λ为升阻比;Wm为叶片前后相对流速矢量平均值;βm为平均相对速度的方向角;γ是转轮叶片周围液体的单位重量。
设叶片进、出口水流相对速度分别为W1和W2,叶片进、出口安装角分别为β1和β2,将x轴设为圆周方向,y轴设为x轴垂直方向,则W1,W2和Wm可记为x轴和y轴方向速度分量的矢量之和:

假设叶片位置角为ζ,可得叶片径向力在X和Y方向的分力为:

式中:ξ=ξ0+ωt,ξ0为所选叶片的初始位置角。
2.2 叶片水力不平衡力
在实际工程中,对于水轮机叶片,由于制造误差、运行中的变形和磨损,出口水流角总是存在差异,导致总径向水推力不为零。这里假设转轮所有叶片中只有一对叶片出口开口不均匀,即存在偏差。定义这一对叶片出口安装角分别为β21,β22,且β22-β21=χ 为安装角偏差。基于式(9)、(13)、(14)和(15),转轮的径向不对称力即水力不平衡力如下:

式中:βm1,βm2分别为这对叶片的平均相对速度的方向角,且表达式如下:


其中,雷诺数为3.5×105,2.2×105和0.5×105时,升力系数CL和升阻比λ分别按式(3)~(8)计算。
2.3 水轮发电机组非线性动力学数学模型
发电机转子(o1)与水轮机转轮(o2)的坐标关系[23]如图3所示。

图3 水轮发电机轴系统的坐标关系Fig.3 Coordinate relationships of the HGU shaft system
根据图3,发电机转子(o1)与水轮机转轮(o2)的坐标关系如下:
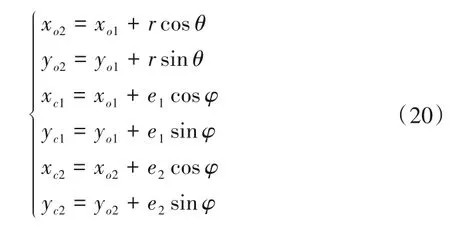
式中:(xo2,yo2)为水轮机转轮轴坐标;θ0为水轮发电机组的初始角度,θ=ωt+θ0;Φ0为发电机转子的初始角,Φ=ωt+Φ0;r是o1和o2之间的距离;e1和e2分别为发电机转子和水轮机转轮的质量偏心量。
水轮发电机组的拉格朗日函数定义为动能和势能之差,可表示为:

进而可得水轮发电机组轴系统非线性动力学数学模型如下:

式中:Fx-ump,Fy-ump为不平衡磁拉力[23];Fx-oil,Fy-oil为油磨力[23];Fx-f,Fy-f为阻尼力[23];Fx-rub,Fy-rub为碰磨力[25]。
3 计算与分析
采用龙格-库塔法进行数值模拟,分析了雷诺数为0.5×105,2.2×105和3.5×105三种情况下,叶片出口安装角偏差(χ)对水轮发电机组非线性动态特性的影响。步长为0.01,每次模拟迭代步长为5 000 步,计算指定的初始值[23]为[xo1,vx,yo1,vy]=[0.000 1,0.000 1,0.000 1,0.000 1]。此外,根据参考文献[23-26],计算中涉及的参数取值如下:m1=1.5×104kg,m2=1.1×104
kg,c=6.5×104N·s/m,k1=8.5×107N/m,k2=6.5×107N/m,e1=0.000 5 m,e2=0.000 5 m,i=800 A,m3=1.0×103kg,ω=3.925 rad/s,Δd=0.000 106 8 m,l=5.0 m,Δl=0.000 2 m,μ0=4π × 10-7H/m,δ=0.008 m,f=0.012,Kc=3×107N/m,Q=42.86 m3/s,D1=2.0 m,b0=0.5 m,Φ=0 rad,θ0=1 rad,φ0=0.8 rad,α=0.136 rad。
3.1 模型动态特性比较
为了研究水力不平衡力对HGSS 振动性能的影响,并验证本文模型的合理性,将本文模型与文献[23]模型的结果进行了对比,如图4所示。文献[23]中没有考虑水力不平衡力因素,本文模型的轴心坐标(xo1和yo1)的振动幅值远远大于文献[23]中模型的振动幅值,说明水力不平衡力会加剧HGSS 的振动。事实上,在实际水电站中已经检测到水力不平衡力的影响,其典型特征正是HGSS的振动幅值被放大。

图4 轴心位移动态特性比较Fig.4 Comparison of dynamic characteristics for axis coordinates(xo1 and yo1)
3.2 叶片出口安装角偏差(χ)对机组振动的影响
在雷诺数为0.5×105,2.2×105和3.5×105三种工况下,水轮发电机组轴心坐标(xo1和yo1)随叶片出口安装角偏差(χ)变化的分岔图如图5、6和图7所示,其中图5(a)、图6(a)和图7(a)为轴心横坐标(xo1),图5(b)、图6(b)和图7(b)为轴心纵坐标(yo1)。

图6 轴心坐标分岔图(Re=2.2×105)Fig.6 Bifurcation charts of axis coordinates(Re=2.2×105)
由图5、6和图7可得,随着叶片出口安装角偏差(χ)从0 rad增大到0.091 rad,水轮发电机组轴心坐标(xo1和yo1)一开始保持幅值较小的两周期振荡,然后进入短暂的且幅值较小的混沌1状态,紧接着又从混沌状态1进入周期振荡,且振动幅值越来越大,并且还出现了HOPF分岔现象,最后从分岔进入永久的混沌状态2,且振动幅值较大。

图5 轴心坐标分岔图(Re=0.5×105)Fig.5 Bifurcation charts of axis coordinates(Re=0.5×105)
除此之外,比较图5、图6和图7可以发现,Re=0.5×105时,水轮发电机组轴心坐标(xo1和yo1)在0.008 754 rd<χ<0.015 87 rad时进入混沌1 状态,在χ>0.084 25 rad 时进入混沌2 状态;Re=2.2×105时,水轮发电机组轴心坐标(xo1和yo1)在0.008 206 rd<χ<0.014 04 rad 时进入混沌1 状态,在χ>0.075 86 rad 时进入混沌2状态;Re=3.5×105,水轮发电机组轴心坐标(xo1和yo1)在0.006 383 rd<χ<0.011 31 rad 时进入混沌1 状态,在χ>0.055 07 rad 时进入混沌2 状态。基于以上分析,随着雷诺数的增大,一方面我们可以得到水轮发电机组轴心坐标(xo1和yo1)的混沌1和混沌2 现象都前移了;另一方面,混沌1 的区间范围变化不大,但是混沌2 的区间范围明显增大了,意味着随着雷诺数增大,水轮发电机组轴心坐标(xo1和yo1)在叶片开口不均匀下更容易出现运行不稳定现象,也就是说随着雷诺数的增大,很小的叶片出口不均匀的误差就能对机组的稳定运行构成威胁。
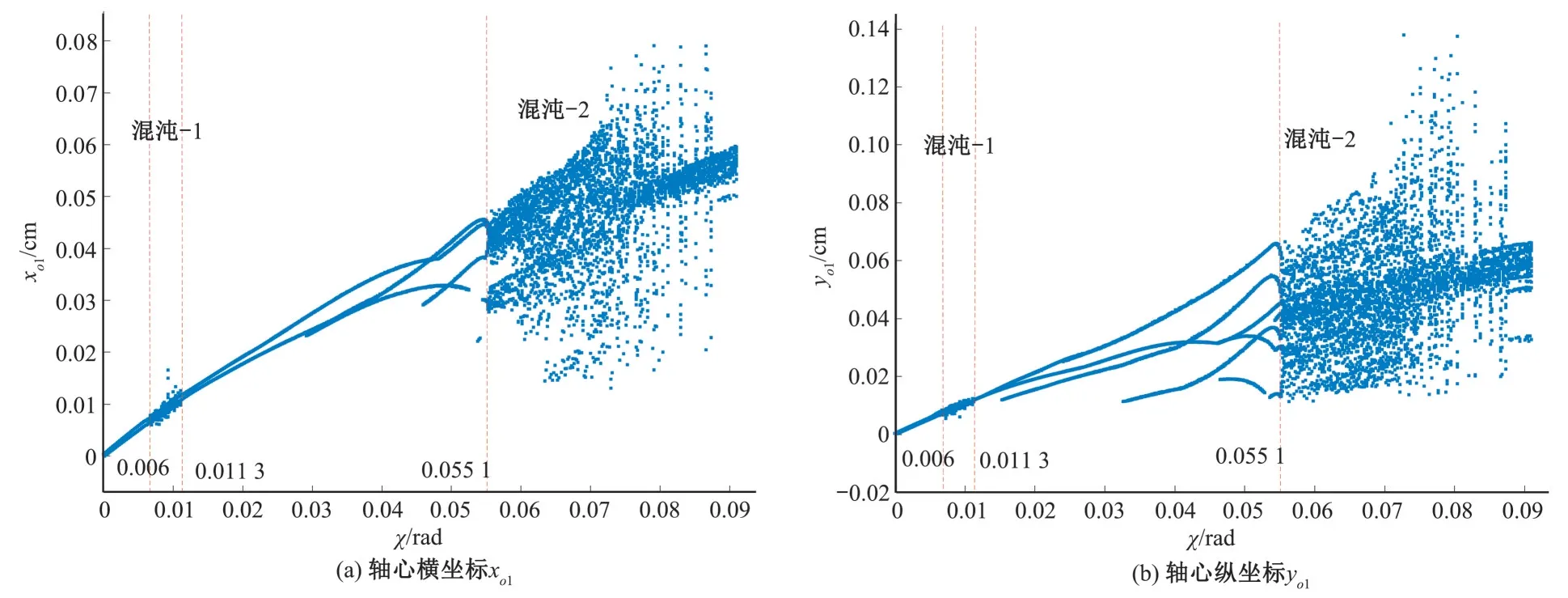
图7 轴心坐标标分岔图(Re=3.5×105)Fig.7 Bifurcation charts of axis coordinates(Re=3.5×105)
4 结论
本文首先提出一种采用SA 单方程紊流模型计算NACA2415 翼型升、阻力系数的方法,然后基于儒可夫斯基定理,建立了非对称翼型叶片的水力不平衡力数学模型。结合不平衡磁拉力和碰磨力,建立了一个包含攻角和雷诺数的水轮发电机组水机电耦合故障非线性数学模型,并通过计算分析,研究了雷诺数和叶片出口安装角偏差(χ)对水电机组振动特性的影响,且得到了以下结论:
(1)随着叶片出口安装角偏差(χ)从0 rad增大到0.091 rad,水轮发电机组轴心坐标(xo1和yo1)都经历两周期振荡-混沌1 状态-两周期振荡-多周期振荡-HOPF分岔-混沌2状态。
(2)Re=0.5×105时,水轮发电机组轴心坐标(xo1和yo1)稳定范围为0 rad<χ<0.008 754 rad,0.015 87 rad<χ<0.084 25 rad;Re=2.2×105时,稳定范围为0 rad<χ<0.008 206 rad,0.014 04<χ<0.075 86 rad;Re=0.5×105时,稳定范围为0 rad<χ<0.006 383 rad,0.011 31 rad<χ<0.055 07 rad。
(3)随着雷诺数的增大,水轮发电机组轴心坐标(xo1和yo1)的混沌现象前移,即在高雷诺数情况下,水轮发电机组轴心坐标(xo1和yo1)在叶片开口不均匀下更容易出现运行不稳定现象。本文研究成果将有利于水轮机的优化设计,并对水轮发电机组安全运行提供参考依据。
