一种角度自适应的椭圆模板检测器

胡永利，武剑，孙艳丰

（北京工业大学人工智能与自动化学院，北京 100124）

1 引言

近年来，随着深度学习的兴起，基于卷积神经网络［1］［2］(Convolutional Neural Networks,CNN）的 深 度学习算法不断刷新诸如图像识别、目标检测、语义分割、姿态估计等各类视觉任务的性能上限。相较于传统的特征提取器，卷积神经网络能够自动从图像数据中学习到各个层次的视觉特征，浅层的卷积神经网络可以提取图像的边缘、纹理等低级特征，深层的卷积神经网络则可以提取出图像的高级抽象特征。整个网络的学习过程无需手工设计参数，与此同时，随着硬件性能的不断提高，加快了卷积神经网络算法的落地和应用。

自2014年以来，涌现出了许多基于卷积神经网络的目标检测算法，这类算法大体上都包含三个部分：首先利用卷积神经网络提取图像特征，之后处理图像特征信息从而完成对物体的类别预测和定位。目前已有的优秀目标检测算法包括，基于锚框的目标检测算法Fast RCNN［3］、Faster RCNN［4］、SSD［5］、YOLO［6］［7］［8］等，以及摆脱锚框的目标检测算法CenterNet-Keypoint［9］、CenterNet［10］、FCOS［11］、Corner-Net［12］等。这些优秀的方法为目标检测的应用及落地创造了可能，具有很高的应用价值。

虽然上述目标检测算法均采用了不同的模型结构，但受限于数据集的影响，这些算法通常使用矩形框来进行检测。例如，现有常用的两个公开目标检测数据集VOC［13］，COCO［14］均采用矩形框进行标注。如图1(a）所示，如果检测对象存在倾斜的角度，那么矩形框将会包含很多背景区域。在提取图像特征的过程中，由于目标物体包含了大量的背景区域，势必会对网络的分类性能造成影响。于是近些年在遥感和文本图像检测方面，出现了一些基于旋转矩形框的目标检测算法，例如R3Det［15］、RoI Transformer［16］、GlidingVertex［17］、RRPN［18］等。旋转矩形框改善了矩形框的问题，但在面对自然图像中复杂的物体时候，依然会包含较多的背景区域，如图1(b）所示。另外，这类算法由于需要额外学习一个倾斜角度参数，导致锚框的使用成倍增加，进而使计算复杂度大幅上升。因此，设计一种能够在不同场景、姿态和方向上均能准确检测物体边界的模型是非常有价值和现实意义的工作。如图1(c）所示，若采用旋转椭圆框进行检测则能够更好地适配物体的轮廓。另外据我们所知，目前没有以椭圆框进行标注的自然场景下的数据集。因此，我们希望通过构建一个以旋转椭圆框标注的自然场景下的数据集，推动越来越多的研究者研究椭圆框目标检测器。

图1 不同形式检测框

2 椭圆模板检测器

2.1 符号表示

图2 EllipseNet网络结构图

2.2 网络结构

如图2所示，原始图像首先经过ResNet50来提取出不同尺度大小的特征图C3-C5。其中C5包含了丰富的语义信息，但随着下采样率的增加导致C5上包含的小物体的有效信息逐渐较少。而浅层特征图C3包含了小物体的边缘信息但语义信息不足。为了融合不同特征层之间的语义信息，本文采用特征金字塔网络（Feature Pyramid Network，FPN)，FPN首先使用一个的卷积核来将C2-C5的通道数目统一变成256，之后相邻特征层借助上采样来自上而下的融合不同特征层之间语义信息，最终经过FPN得到了四张融合后的特征图F1-F5，后续分别用于完成图像的分类和定位。

在得到F1-F5之后，EllipseNet的回归层部分则是在各个特征层的基础上用以预测椭圆的类别及属性（圆心位置、长短轴长和旋转角度)。然而在实际实验过程中，如图3(a）所示，观察到FCOS预测出物体的中心位置会跟实际的中心发生偏移，究其原因是由于特征图下采样丢失精度以及FCOS会在中心区域附近选择正样本。为了弥补圆心偏移的损失，在预测层中额外回归了圆心偏移量。假设第i个特征图Fi中的某个位置坐标为，则该位置和圆心之间的真实偏移量如公式（1）所示：

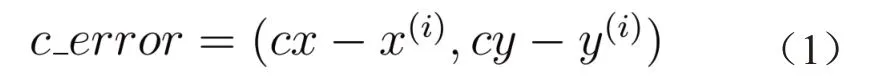
图3 FCOS和EllipseNet检测效果图

2.3 正负样本选择

EllipseNet正样本的选择采用了FCOS算法的思想，即首先将每个特征图的像素位置映射回原图尺度，若特征图的某个位置落在了真实框内，则将其视为正样本的一个必要条件；之后如公式（2）所示，设计了一个中心采样比例系数，分别为每个特征层Fi根据其下采样步长设定了一个半径r，将特征图上的像素位置在半径范围内的视为正样本的另一个必要条件；

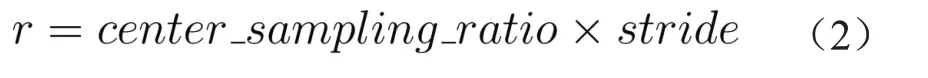
但此时并没有考虑FPN结构按照各自特征图尺度分配正样本的原则，故又额外设计了regree_ranges参数，该参数为每个特征图Fi设计了一个尺度范围scale，若正样本的最长边落在某个scale内，则该特征层负责预测该物体，其余特征层则视为负样本。

在完成上述正样本分配后，如图4所示，此时依然存在一个正样本点可能同时匹配两个真实框的情况，而本文做法则是直接按照面积匹配最小原则将当前正样本点匹配给面积最小的真实框。

图4 正样本点匹配两个真实框示意图

2.4 损失函数

EllipseNet整体损失函数如公式（3）所示：

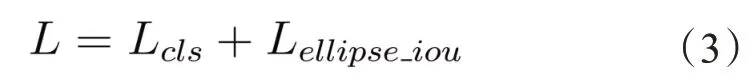
其中Lcls表示类别损失，而表示椭圆的交并比损失。考虑到任意形状的两个椭圆的交并比存在运算强度大的缺点。因此，为了加速网络的训练，重新定义的损失函数为：

另外，本文还额外引入了一种椭圆交并比损失函数，如图5所示，令和分别表示椭圆的真实长短轴长和预测长短轴长，则

图5 椭圆交并比损失函数

两个椭圆的近似交并比如公式（8）所示：

由于交并比需要优化到1，最终的椭圆交并比损失为：

当然在模型训练初始阶段，网络还不能够准确的预测椭圆的旋转角度和中心偏移量，因此椭圆交并比损失是在模型训练稳定后才被添加进去的。

2.5 推理过程

给定一张输入图像后，经过FPN得到五张特征图，之后经过回归层之后每张特征图的每个位置会得到五个预测值：类别置信度分数、中心度分数、椭圆中心偏移量、长短轴长以及旋转角度。然后将特征图所有像素点映射回原图，将类别置信度分数和中心度分数相乘得到最终每个像素点的置信度分数，另外，本文设定一张图最多只检测个物体，并通过一个分数阈值来过滤掉低于阈值的像素点。在得到预测点之后，再通过公式（1）来修正这些点的位置便得到了椭圆圆心的位置，另外在结合对应位置其他预测值（长短轴长，旋转角度）便得到了预测椭圆框，最终经过椭圆的NMS便得到了最终的输出结果。

3 实验结果

3.1 数据集

据本文所知，目前没有用旋转椭圆框标注的自然场景下的数据集。为了测试EllipseNet在自然场景数据集上的性能，本文在PASCAL VOC2007数据集基础上构造了一个旋转数据集，其中原始的PASCAL VOC2007数据集包含了丰富的自然场景，该数据集总共标注了20个类别的物体。但由于PASCAL VOC2007数据集中物体大多数垂直于地面，为了增加角度的多样性需要对该数据集进行旋转。本文通过使用传统的图像处理算法等比例的旋转图像并人为的用旋转椭圆框对物体进行了标注。本文将构造完成的数据集称为Rotate VOC2007数据集，该数据集总共包含了5,747张图像，其中4,981张图像用于训练，766张图像用于测试，总共包含了隶属于20个类别的18,445个旋转的物体。

3.2 对比方法

本文选择了目前性能优异的旋转检测算法和EllipseNet做对比，包括一阶段旋转检测算法和二阶段旋转检测算法。其中，一阶段检测算法包括：

(1)RetinaNet-OBB［21］，一种借助水平锚框的高效旋转检测算法。

(2)FCOS-Poly［11］：在FCOS算法基础上结合Poly-IoU-Loss损失函数进行旋转检测的算法。

(3)Gliding Vertex［17］：一种在预测水平矩形框基础上额外再预测四个角点偏移量的旋转检测算法。

(4)R3Det［15］：一种通过引入特征微调模块来克服旋转候选框特征不对齐的旋转检测算法。

与上述一阶段旋转检测算法相比，二阶段旋转检测算法由于额外增加了一个RPN模块其性能普遍较好，但随之带来的缺点就是检测速度相对较慢。本文选择的二阶段检测算法包括：

(1)R2CNN-OBB［4］：一个在FasterRCNN基础上改造的直接预测旋转框的二阶段检测算法。

(2)RoI Transformer［16］：一种借用水平锚框并借助RoI Learner模块学习水平锚框到旋转锚框变换的二阶段检测算法。

(3)Oriented RCNN［22］：一种借助Oriented RPN模块学习水平锚框到旋转锚框变换的二阶段目标检测算法。

3.3 超参数设置

本文将数据集R-VOC2007中图像统一变换成［512,800,3］大小。另外，在模型训练过程中，使用了随机上下、左右翻转的图像增强方法。模型总共迭代了100轮，并将初始学习率设置为5e-5。使用Adam［23］优化器并以批次2对模型进行训练。在正负样本选择过程中，令中心采样率，各特征图下采样率为。在损失函数计算过程中，将Focal Loss的两个超参分别设置为和，将权重系数分别设置为，。

本文采用的硬件平台为因特尔的i9-10900X CPU和一块显存为24GB的英伟达3090显卡，Pytorch采用的版本为1.7.1。

3.4 实验结果分析

表1展示了EllipseNet和其他旋转检测算法的性能比较。从表中可以看出，二阶段目标检测算法RoI Transformer和一阶段目标检测算法Gliding Vertex分别以48.27%和46.06%的mAP值取得了最优的性能。虽然EllipseNet仅取得了38.71%的mAP值，但在汽车和自行车两个类别上分别击败了其余所有的方法，这也在一定程度上验证了本文方法在面对复杂的自然场景时也具有一定的性能优势。

表1 RVOC2007数据集实验结果对比

3.5 消融实验

(1）椭圆中心回归：一个椭圆的中心对确定一个椭圆框的位置非常重要。虽然FCOS能够预测物体的中心区域，但在一定程度上，如图3(a）所示，依然会存在一定的偏差。表2展示了是否添加椭圆中心偏差分支的消融实验，从中可以看出，在额外回归椭圆圆心偏差后mAP有1.4%的提升，从而验证了椭圆中心对预测椭圆位置的重要性。

表2 椭圆中心偏差分支消融实验

(2）椭圆交并比损失函数：表3展示了不同损失函数对EllipseNet性能的影响，从表中可以看出，相较于仅使用Smooth L1 Loss［4］，在添加了椭圆交并比损失后EllipseNet的mAP涨了0.9%，从而验证了椭圆交并比损失函数能够进一步的提升模型的性能。

表3 损失函数消融实验

3.6 可视化分析

如图6所示，本文可视化了EllipseNet在RVOC2007数据集上的部分检测结果，可以看出，在复杂的自然场景下EllipseNet能够较好的检测各个角度姿态下的物体。

图6 RVOC2007可视化

4 结论

本文提出了一种能够更加精确检测物体的旋转椭圆目标检测器EllipseNet，设计网络结构使其预测椭圆的圆心偏移量、长短轴长以及旋转角度来完成旋转椭圆的预测。另外在损失函数部分，考虑到椭圆框本质上应该作为一个整体来进行损失计算，而不应该用Smooth L1 Loss来单独回归椭圆框的各个属性，因此本文额外又提出了一种椭圆交并比损失函数来进一步提升了模型的性能。最终实验表明，EllipseNet具有一定的应用价值。