基于康达效应的电源箱体散热优化研究

2022-12-26高海军张林华马桤政宋永兴

山东建筑大学学报 2022年6期

高海军张林华马桤政宋永兴

(山东建筑大学热能工程学院，山东济南 250101)

0 引言

电磁感应加热技术是利用电磁感应原理产生交变磁场，将被加热工件置于交变磁场中，工件内产生涡流从而使得工件发热的方法，是一种非接触式的加热方式，相比于传统接触式加热方式，电磁感应加热具有安全可靠、节能环保、加热效率高、智能可控等优点[1]，已广泛应用在航空航天、金属材料热处理、车辆制造、和焊接等领域[2-3]。

近年来，随着电力电子技术和器件的迅速发展，如绝缘栅双极型晶体管(Insulated Gate Bipolar Transistor， IGBT)的问世，以及集成电路的不断发展，极大地促进电磁感应加热电源向着高效率、高性能方向发展。电源频率和功率也越来越高，箱体结构也越来越紧凑，各器件的产热量迅速增加，箱体内部空气流动不畅导致元器件温度迅速升高，而电子设备的可靠性与设备的温度息息相关。根据研究[4]表明，近60%的电子设备故障是由温度引起的，并且在工作环境温度每升高10 ℃，故障率几乎增加了一倍，箱体的散热问题成为亟需解决的问题。

有关IGBT 模块散热，林媛等[5]提出一种新型适用于高散热量电子元件的热翅板式散热器，并运用FLUENT 软件模拟分析了该新型散热器的散热性能，最终得到了不同热功率下对应的最佳冷却风量。李阳等[6]针对IGBT 模块散热问题，通过实验和模拟研究了IGBT 风冷散热器散热特性，分析了翅片高度和厚度以及风机风量对散热器热阻的影响，最终得到最优方案。DONG 等[7]设计了一种针状形翅片结构的新型散热器，增强了IGBT 元件冷却效果，结果表明针状翅片直径比高度对传热量的影响更大，而对于冷却均匀性而言，翅片高度比直径影响更大。关于干式变压器散热，王凯东等[8]基于热-流耦合方法，通过数值模拟研究了箱式变压器室的通风散热特性，分析了风速、进风口个数和出风口面积对通风散热效果的影响。吴红菊等[9]模拟计算强迫风冷条件下变压器温度场并优化不合理位置，通过改变风口位置使变压器温度下降了约8℃。

在贴附射流方面，邱少辉等[10]提出一种条缝型送风口形成的竖壁贴附射流，利用二维粒子图像测速技术研究了送风速度对气流组织和贴附距离的影响，结果表明送风速度越大，贴附效果越强，贴附距离越长。JANBAKHSH 等[11]通过实验研究了喷嘴送风形式下的壁面贴附射流，发现速度和温度分布具有自相似性。CAO 等[12]利用粒子图像测速技术研究了顶壁贴附射流的湍流流动特性。尹海国等[13]提出了一种基于方形柱面的竖壁贴附射流，得到了轴线速度、温度分布的计算公式。

文章针对采用强迫风冷式散热的电源箱，根据康达效应修改进风口形状，从而优化箱内流场，运用FLUENT 软件进行数值模拟获得箱体内部温度场和流场，以期为解决电源箱内部元件温度过热问题提供依据。

1 康达效应基本原理

康达效应(Coanda Effect)亦称为附壁效应，即射流流体偏离原来方向，趋向于相邻固体壁面的现象[14]，如图1 所示。当流体从孔口射入周围环境时，会对周围环境流体产生卷吸作用，导致射流两侧产生压力差，并且附壁侧低于另一侧，使得射流趋向固体壁面侧[15]。利用康达效应在变压器表面形成贴附射流，可提高变压器表面流速。

图1 康达效应示意图

射流主体断面速度分布由式(1)[16]表示为

式中u为射流主体断面速度，m/s；um(y)为距送风口y处断面上的轴线速度，m/s；y为竖直方向距送风口的距离，m；η为无因次距离，等于对应断面上某一速度所在位置高度与0.5um速度所在位置高度(h0.5)的比值，即y/ h0.5。

竖壁贴附射流的轴线速度衰减公式由式(2)[17]表示为

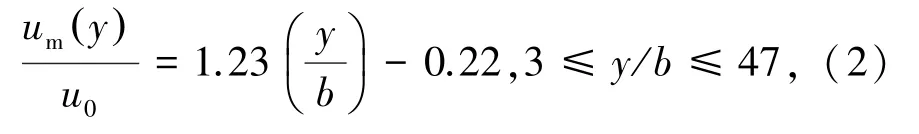
式中u0为送风口速度，m/s；b为送风口的宽度，m。

2 模型建立

2.1 物理模型

功率为80 kW 的中频感应加热电源结构如图2所示，其尺寸为600 mm×720 mm×800 mm(长×宽×高)。电源箱体内包括主控板、中频变压器、布线、电源开关、IGBT、散热器、电抗器、谐振电容组、隔直电容组、风机等，其中主要发热元器件为中频变压器和两个IGBT 模块。箱体内部元器件尺寸见表1。箱体内部结构复杂、元器件较多，全部建模数值模拟比较困难，因此把体积较小、无发热量的、对流场和温度场影响不大的元器件忽略，简化了模型。

表1 箱体内部元器件尺寸参数表

图2 箱体内部结构示意图

根据中频变压器的形状，依据康达效应修改原模型底部进风口的形状。修改前、后的底部进风口形状分别如图3(a)、(b)所示，图中阴影部分为进风口形状。在模拟箱体内部温度场和流场时，只改变底部进风口形状，其他参数均保持不变。

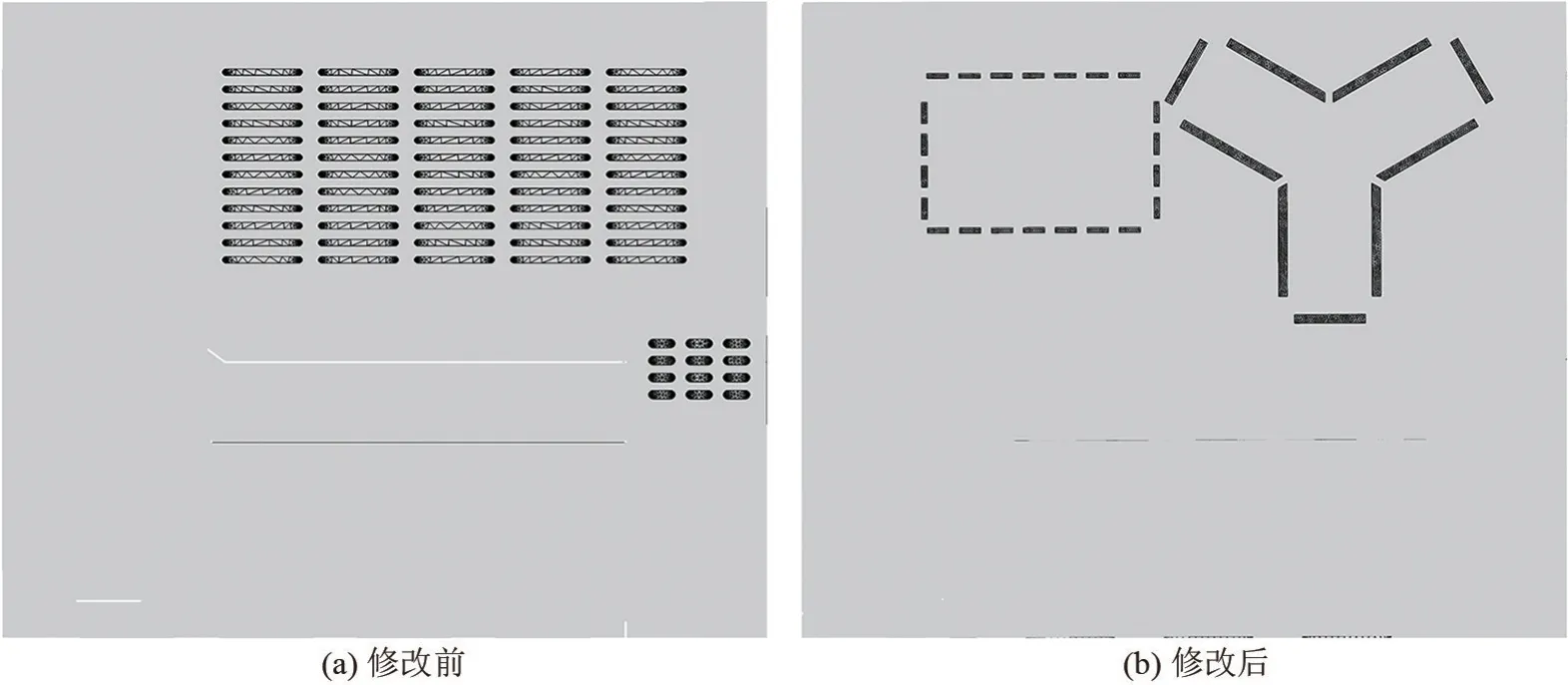
图3 底部进风口形状示意图

2.2 数学模型

流体流动与传热过程中基本遵循质量守恒定律、动量守恒定律和能量守恒定律[18]。

连续方程由式(3)表示为

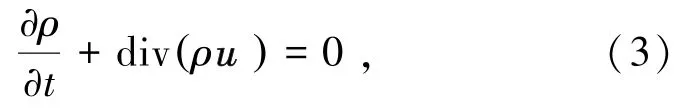
式中ρ为密度，kg/m3；t为时间，s；u 为速度矢量，m/s。

动量守恒方程由式(4)～(6)表示为

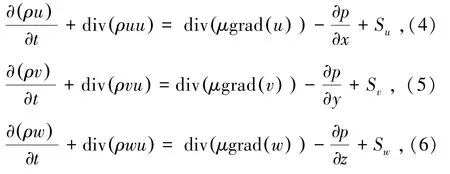
式中u、v、w为速度矢量在x、y、z方向上的分量，m/s；μ为动力黏度，Pa·s；p为压强，Pa；Su、Sv、Sw为广义源项。

能量守恒方程由式(7)表示为

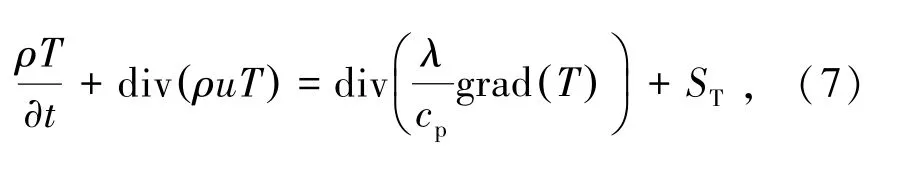
式中λ为导热系数，W/ (m·K)；ST为源项；cp为定压比热容，J/ (kg·K)；T为温度，K。

选择标准k - ε湍流模型，湍动能k方程由式(8)表示为

湍动耗散率ε方程由式(9)表示为

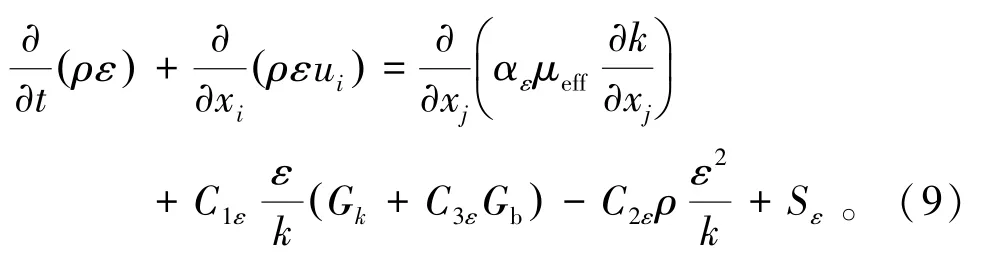
式中Gk为层流速度梯度所产生的湍流动能，J；Gb为浮力所产生的湍流动能，J；Ym为可压缩湍流中脉动动量增益；C1ε、C2ε、C3ε为经验常量；αk和αε分别为k方程、ε方程的湍流普朗特数；Sk和Sε为源项；μeff为有效动力黏度，Pa·s。

2.3 边界条件的设定

进口设置为压力入口，进口温度设置为300 K；出口设置为质量流量出口，质量流量为1.93 kg/s。将中频变压器和两个IGBT 模块设置为内热源，假定变压器与IGBT 散热是一个稳态过程，其散热量分别为2.0和1.5 kW，热释放率分别为254.7 和1 071.4 kW/m3。元器件与空气的传热采用流固耦合传热。散热方式主要为强迫对流换热，忽略元件之间的辐射换热；同时也忽略箱体外壁面的辐射换热，采用绝热边界。采用coupled 算法求解。修改前与修改后模型均采用相同边界条件。模型修改前网格数量为8 439 399，修改后网格数量为9 272 347。

3 数值模拟结果分析

3.1 温度分析

3.1.1 变压器温度

选取变压器某一表面进行温度分析，提取表面上点做温度随进风口距离变化的曲线图，如图4 所示，横坐标正方向表示距底部进风口的距离越来越大。修改前后的温度变化趋势大致相同，随着距离的增加，温度先逐渐升高后略微下降。因为变压器散热方式主要为对流换热，空气从底部进风口进入温度较低，与变压器的温差大，且底部换热面积大，则散热效果好、温度低。随着距离的增加，空气温度也随之升高，导致温差逐渐减小，散热效果减弱，所以温度逐渐升高。但到达一定距离，变压器上表面与空气进行换热，增大了换热面积，散热效果有所提高，所以温度开始有略微下降。对比修改前后的温度变化曲线，修改前最高、低温度分别约为384、377 K，修改后最高、低温度分别约为355.5、353 K，温度整体大约降低了25 K。

图4 变压器表面温度变化曲线图

取变压器中心上的点，做温度随进风口距离变化的曲线图(如图5 所示)。修改前后的温度变化趋势与表面温度变化趋势基本相同，但整体温度比表面温度高约3 K。因为中频变压器内部不能与空气直接接触，散热先要通过导热的方式将热量传递到变压器表面，再通过对流换热将热量带走，内部散热热阻比表面散热热阻大，所以散热效果差，温度较表面温度高。对比分析修改前与修改后的温度变化曲线，可以明显看出修改后的中心温度整体低于修改前的温度，大约降低了25 K，与变压器表面结果相一致。

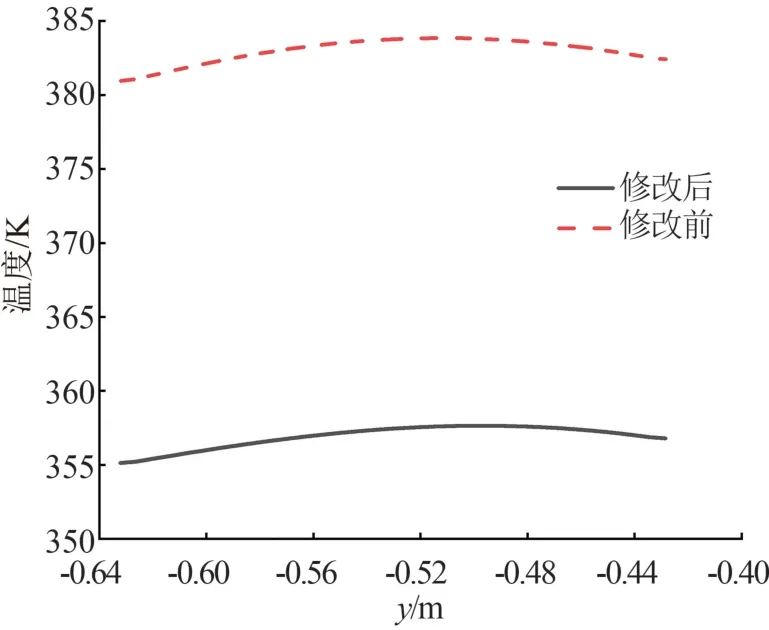
图5 变压器中心温度变化曲线图

在变压器的上、中、下3 个位置做剖面，在y方向的坐标分别为-0.6、-0.53 和-0.45 m，得到温度变化云图，分别如图6～8 所示。从变压器中心到变压器表面成逐渐降低的温度梯度，内外温差大约在3.0 ～4.0 K，这与温度曲线得出的结果一致。选择3 个截面的最高温度进行比较，在y＝- 0.60、-0.53 m、-0.45 m 处，最高温度分别为383.0、384.0、383.0 K。距离底部进风口越来越远，温度先升高后降低，与变压器温度变化曲线图结果相吻合。

图6 y＝-0.60 m 处温度分布图

图7 y＝-0.53 m 处温度分布图

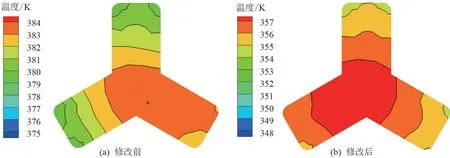
图8 y＝-0.45 m 处温度分布图

对比相同位置修改前、后温度云图进行对比。y＝-0.60 m处，修改前最高、最低温度分别为383 和379 K，而修改后最高、最低温度分别为357 和353 K，变压器温度发生明显的下降，温度约降低了26 K。对比最高温度所占区域，修改前的最高温度区域远大于修改后的，说明修改后温度更加均匀，变压器的整体温度更低，散热效果更好。

3.1.2 IGBT 模块温度分析

IGBT 模块的温度变化曲线如图9 所示，横坐标正方向表示距离散热器越来越近。修改前后的IGBT 模块的温度都是随着距离减小而逐渐降低。IGBT 模块的热量主要通过导热的方式传导至IGBT的基板上，再传递到散热器上，最终通过散热器散热片与空气进行对流换热。散热器的翅片增加了换热面积，提高散热量。远离散热器靠近空气的一侧，相对导热热阻较大，所以散热效果较差，故随距离的减小，温度逐渐降低。

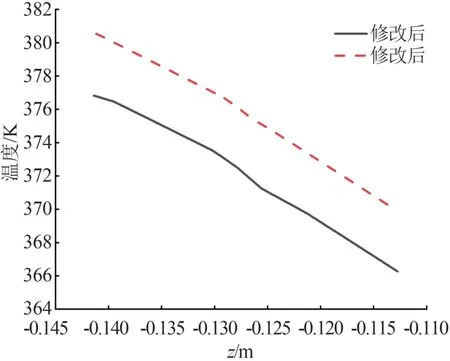
图9 IGBT 模块温度变化曲线图

比较修改前后IGBT 的温度变化，可以看到修改前的温度曲线均在修改后温度曲线的上方，说明修改后整体低于修改前的温度，大约降低了4 K，修改后的散热效果比修改前更好。

沿IGBT 模块和散热器中心做剖面，得到温度云图，如图10 所示。可以更加直观地看到IGBT 的温度梯度，距离散热器越近，温度越低。对比修改前与修改后IGBT 温度云图，发现修改后比修改前温度降低4 K，与温度变化曲线结果相一致。

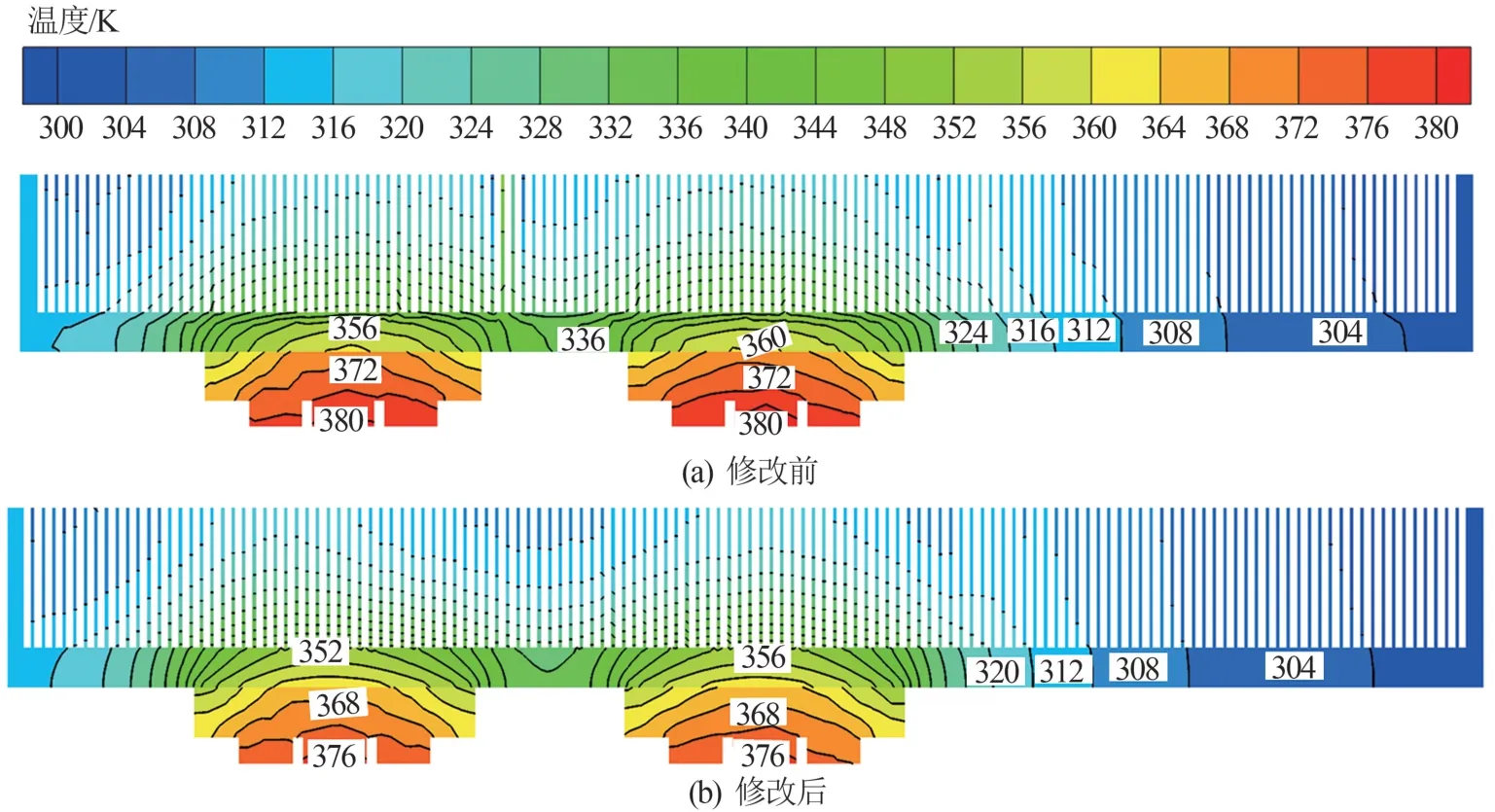
图10 IGBT 及散热器温度分布图

3.1.3 整体温度分析

沿IGBT 和变压器的中心(x＝0.12 m 处)剖面，可以同时看到主要的发热元件，能更加直观看到箱体内部的温度场，其温度变化云图如图11 所示。通过局部温度场和整体温度场，均可发现修改后的温度更低，散热效果更好。

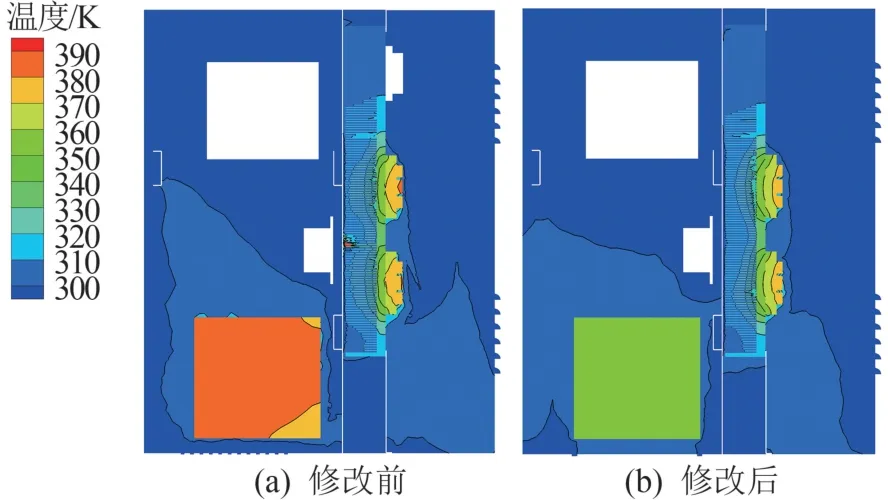
图11 x＝0.12 m 截面箱体内部温度分布图

各元器件的平均温度见表2。修改前，中频变压器和IGBT 模块的平均温度分别为382.3 和369.0 K，修改后的平均温度分别为356. 1 和365.0 K，分别下降了约26.2 和4.0 K。

表2 各元器件平均温度表单位:K

3.2 速度分析

随机选取变压器某一表面附近的点，进行数据拟合得到速度曲线图，如图12 所示。修改前的速度先迅速降低，后在6 m/s 上下波动，最大、最小速度分别约为15、5 m/s；修改后速度趋势呈下降趋势，最大、最小速度分别约为35、25 m/s。可以看出修改后的速度明显大于修改前的速度，速度的大小影响对流换热系数，速度越大，对流换热系数就越大，对流换热量也就越大。

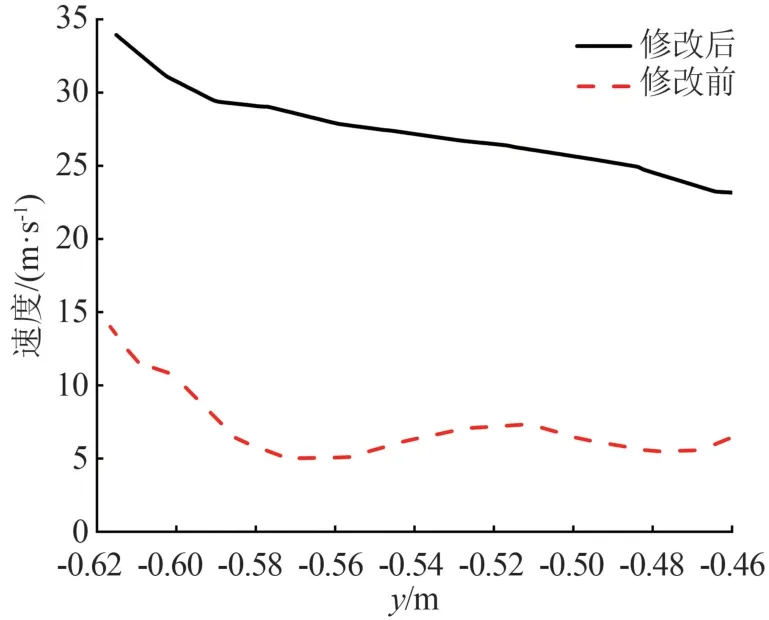
图12 变压器表面速度变化曲线图

同样选取x＝0.12 m 处做速度云图，如图13 所示。修改前，空气进入箱体内部后，气流并未有效地流过变压器表面(红色椭圆)，变压器表面的平均速度约为7 m/s。而修改后，依据康达效应，风口形状和变压器外形相同，空气从风口进入在变压器表面形成贴附射流，提高了变压器表面的平均流速，平均速度约28 m/s，增加了对流换热量。

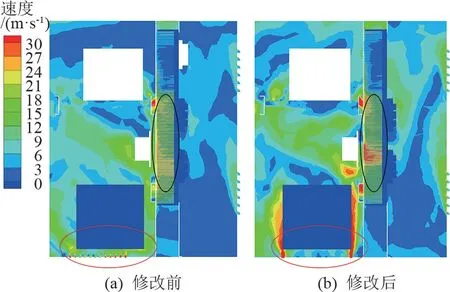
图13 箱体内部速度分布图

对比修改前与修改后散热器(黑色椭圆)的速度，可以看出修改前的最大速度约为23 m/s，而修改后的最大速度约为28 m/s。修改后底部进风口面积减小，前面和侧面进风口的面积保持不变，在总风量不变的情况下，则相对会增加前面与侧面进风口的风量，提高了散热器表面的速度，增强对流换热量。

3.3 对流传热系数分析

选取与速度曲线图相同位置，进行数据拟合得到对流换热系数曲线图，如图14 所示。修改前后对流换热系数变化趋势基本一致，随着距离增加对流换热系数逐渐减小。结合速度变化曲线图，可以观察到对流换热系数的变化趋势与速度变化曲线相一致，影响对流换热系数的因素很多，由于元器件材料、换热表面的形状、部位、流体的物理性质修改前后基本相同，所以换热表面的流速是对流换热系数的主要影响因素。

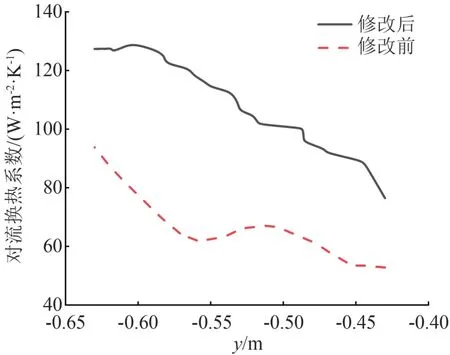
图14 变压器表面对流换热系数变化曲线

对比修改前后的对流换热系数发现，修改前最大、最小换热系数分别约为95 和50 W/(m2·K)；修改后最大、最小换热系数分别约为130 和80 W/(m2·K)。修改后的对流换热系数大于修改前的对流换热系数，因为依据康达效应，修改底部进风口后，空气在变压器壁面形成贴附，有效提高了变压器表面的风速，进而使得对流换热系数得到显著提高，增强散热效果。