中深层地埋管换热器变延米传热模型研究

2022-12-26刘杨贾林瑞崔萍

山东建筑大学学报 2022年6期

刘杨贾林瑞崔萍

(1.山东建筑大学热能工程学院，山东济南 250101；2.香港理工大学建筑环境及能源工程学系，香港 999077)

0 引言

在我国双碳目标下，地热能作为可再生能源，利用其作为建筑暖通空调系统的冷热源具有节能减排的优势，故其规模化开发利用势在必行。根据地热能所处深度，一般将其分为浅层地热能和中深层地热能。浅层地热能是储存在地表至一定深度范围内(一般为200 m)，其温度＜25 ℃，具有一定开发利用价值的地热能[1]。对于浅层地热能开发利用技术而言，地埋管换热器埋深一般为80 ～150 m，且浅层岩土温度通常＜20 ℃，存在可利用温差小的缺点，因此浅层地埋管换热器通常需要一定的占地面积来钻孔埋管[2-4]。除此之外，浅层地热能利用系统还存在由于全年冷热负荷不平衡造成的地下冷/热堆积问题，限制了其地域性应用范围，尤其在寒冷地区的应用。中深层地热能是指贮存在200～3 000 m 地层中的储量丰富、分布广泛、环保清洁的地热能资源。与浅层地热能可利用的地温相比，中深层地埋管换热器能利用的地温可以达到70～90 ℃，相同取热负荷下，所需的占地面积远小于浅层地埋管的面积。同时，由于其较高的地温和较大的换热体，中深层地埋管换热器本身具有良好的地下热平衡性，非常适合用于寒冷地区有单独供热需求的建筑[5-7]。

中深层地埋管传热问题复杂，多数学者采用数值解分析法研究中深层地埋管换热器传热问题。HOLMBERG 等[8]借助有限差分法构建循环液以及岩土节点方程，研究了循环液流向对延米换热量的影响。FANG 等[9]利用交叉差分法构建岩土内部节点方程，采用追赶法求解差分方程组得到岩土温度场。对于地埋管换热器的实际应用而言，简捷的设计计算方法是利用直观的循环液温度解析解模型。PAN 等[10]和FANG 等[11]基于套管式准三维解析解模型，建立综合考虑地温梯度的钻孔内循环液传热解析解模型并验证了其计算精度，该模型可在一定程度上有效提高计算效率。然而，上述解析解模型中未考虑钻孔深度方向换热量不均匀的真实条件。

要实现中深层地埋管换热器的有效应用，关键是要在设计阶段对系统的可持续换热量进行定量计算，进而对工程开展提供有价值的参考意见和改进措施，避免造成不必要的经济、土地浪费等。孔彦龙等[12]采用Beier 解析解法和双重连续介质数值模拟法评估了深井换热技术的换热量，发现无论是短期(4 个月)还是长期(30 a)每天连续从深井取热，延米换热功率上限均≤150 W。方亮[13]、邵珠坤[14]利用交叉差分法对套管式地埋管换热器传热过程进行了数值分析，并通过“名义取热量”评估了地埋管换热器的换热性能。满意等[6]模拟研究了利用弃井开采的中深层地热能，分析了多种因素对地埋管换热器名义取热量的影响，结果表明名义取热量会随着外管管径和外管导热系数的增大而增大，随着内管管径和外管导热系数的增大而减小。

传统的解析解模型将地埋管换热器分为钻孔内与钻孔外两个传热模型，然后以均匀的孔壁温度为耦合温度进行求解。其中在钻孔外的传热模型中，往往将钻孔深度方向的换热量设定为均匀分布，对于地温变化范围高达30～40 ℃的中深层岩土而言，将导致较大的计算误差。因此，文章提出的中深层地埋管换热器解析解模型将基于变延米换热量的真实条件，引入无限长线热源的瞬态热阻，建立由钻孔内循环液至远端岩土的一体化传热模型，通过拉普拉斯变换以及温度叠加原理，得到了中深层地埋管换热器循环液的温度响应解析解。一体化传热模型取消了传统中深层地埋管换热器模型中钻孔壁温均匀的假设，更加符合工程实际。为探讨中深层地埋管换热器的换热性能，利用模型分析多个参数对地埋管换热器最大换热功率以及出口水温的影响。

1 地埋管换热器变延米换热量模型

1.1 物理模型及其传热模型假设条件

在中深层地埋管换热器中通常采用套管式地埋管，钻孔深度一般为1 000～2 500 m。套管式换热器采用同心埋管，携带能量的循环介质从套管外管流入内管流出，或者从内管流入外管流出，完成与周围岩土的热量交换。

为了简化中深层地埋管换热器解析解模型及求解过程，在后续推导模型过程中采用以下假设条件:

(1)岩土热物性参数为常量，不受温度影响；

(2)不考虑地表边界条件影响；

(3)不考虑钻孔内流体、回填材料热容影响；

(4)忽略地下水的渗流对传热的影响；

(5)不考虑循环液、回填材料以及管材在深度方向上的热传导。

模型重点求解循环液的温度响应。利用线性叠加原理，模型中将循环液温度响应看作由初始地温均匀作用下给定热流引起的温度响应与初始地温梯度对循环液温度引起的温度响应之和。

1.2 忽略岩土地温梯度的传热解析解模型

在取热工况下，换热器内循环介质最优流动方向为外进内出式[5，9]。模型中的热阻示意图如图1所示。传统模型往往将地埋管换热器求解区域分为钻孔内与钻孔外两部分分别求解，然后在孔壁处耦合，如图1(a)所示。文章提出的模型不再区分钻孔内外两个求解区域，而是基于线热源模型将外管流体与岩土换热作为一个整体考虑，建立传热一体化模型，如图1(b)所示。

图1 模型中热阻示意图

将埋管视作无限长线热源，钻孔外岩土的瞬态传热热阻R1(t)由式(1)表示为

式中Ei为指数积分函数；rb为钻孔直径，m；a为岩土热扩散系数，m2/s；t为时间，s；ks为岩土导热系数，W/(m·K)。

外管流体至钻孔壁的热阻Rp由式(2)表示为

式中ku为外管导热系数，W/(m·K)；kg为回填材料导热系数，W/(m·K)；ro为外管外径，m；ri为外管内径，m；h为对流传热系数，W/(m·K)。

将外管流体至钻孔壁的稳态热阻与钻孔壁至远端岩土的瞬态热阻进行简单的叠加，即可获得流体至远端岩土的瞬态热阻R′11(t)，由式(3)表示为

内外管循环液之间的热阻R12与传统模型一致，由式(4)表示为

式中ku2为内管导热系数，W/(m·K)；rii为内管内径，m；rio为内管外径，m。

在求解过程中，选取远端岩土初始温度作为过余温度的参考温度，即θ ＝Tf-T0，其中T0为零初始条件下的初始地温，该数值可取钻孔深度方向岩土平均温度。两股循环介质在横截面中的净传热量将各自与其所在轴向的对流传热量平衡，根据能量守恒定律以及假设条件可以得到流体能量平衡方程，由式(5)表示为

令

故内外管温度由式(7)表示为

边界条件由式(8)表示为

式中M为循环液质量流量，kg/s；c为循环液比热容，J/(kg·K)；θf1为外管流体温度，℃；θf2为内管流体温度，℃；q1(z，t)为外管每米取热量，W/m；q2(z，t)为内管每米取热量，W/m；Q为钻孔总取热量，W；H为钻孔深度，m；z为深度坐标，m。

对式(5)进行关于z的拉普拉斯变换，结合式(6)以及边界条件(8)，拉普拉斯变换后得到内外管循环水温度公式，由式(9)表示为

其中，

根据式(6)，延米换热量q1(z，t)、q2(z，t)由式(14)和(15)表示为

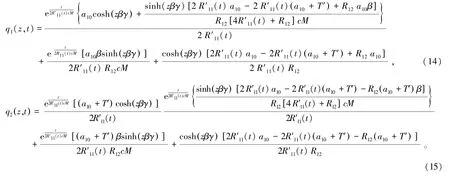
总取热量Q与q1(z，t)、q2(z，t)之间关系由式(16)表示为

1.3 考虑地温梯度的解析解模型

对于浅层埋管而言，地温梯度影响较小，但对于中深层地埋管而言，地温梯度则不可忽视[15]。假设岩土初始地温梯度为初始时刻的热源，并将岩土视为半无限大物体，即z＝0 的表面，始终维持恒定温度T0。假设地温梯度为ΔT，则岩土初始过余温度为θg(z)＝ΔT·z。则初始地温作为假想的虚拟热源所引起的温度响应可由式(7)表示为

该问题的初始条件由式(18)表示为

所以地温梯度对岩土体的温度响应可由式(19)表示为

式中z′为积分坐标。

基于岩土体温度响应已知，即假设钻孔壁温已知，在计算地温梯度对钻孔内循环液温度响应时，可将钻孔内及循环液简化为均匀的回填材料，则钻孔内回填材料传热由式(20)表示为

该问题的边界条件由式(21)表示为

运用分离变量法求解得式(22)

式中Δθ1(r，z)、Δθ2(r，z)分别由式(23)和(24)表示为

式中βm、μm均为特征值；Jn(x)、In(x)为n阶贝塞尔函数。

故考虑地温梯度影响下的循环液温度由式(25)表示为

2 模型验证对比

为验证解析解模型的有效性，利用FANG 等[9]建立的数值模型进行验证。用于模型验证的基本参数见表1。

表1 基本参数表

连续2 880 h 从岩土提取热量150 kW，数值解及解析解计算所得的循环液进出口温度随时间的变化曲线如图2 所示。可以看到，循环液外进内出取热时，解析解模型计算得到的温度与数值解模型计算的结果具有相同的变化趋势，计算结果吻合较好。运行2 880 h 后，循环液进出口温度误差分别为0.72%、0.55%。因此，该解析解模型可有效预测中深层地埋管换热器中循环液的温度分布。

图2 循环液温度随时间的变化曲线图

3 影响因素分析

3.1 最大换热功率

以“最大换热功率”来衡量中深层地埋管换热器换热性能。根据文献[5]和[13]规定的最大名义取热量，地埋管进口温度在取热期间不得＜5 ℃，此时达到最大换热功率。

以表1 基本参数为例，利用上述解析解模型反复试算求得，当恒定取热为225.5 kW 时，2 000 m 钻孔深度连续运行2 880 h，地埋管进、出口水温分别为5.00、9.45 ℃，所以该工况下2 000 m 钻孔深度的换热器最大换热功率为225.5 kW，每米钻孔最大换热功率为112.75 W/m。流体进出口温度随时间的变化如图3 所示。

图3 不同时刻地埋管进出口水温随时间变化曲线图

3.2 钻孔深度的影响

保持基本参数不变，改变钻孔深度，不同钻孔深度地埋管换热器的最大换热功率如图4 所示。可以得出，随着钻孔深度的不断增加，地埋管换热器的最大换热功率也随之增加。这是因为在地温梯度的影响下，随着钻孔深度增加，岩土的平均温度随之升高，地埋管换热器单位长度的换热温差逐渐增大，即地埋管的最大换热功率也随之增加。在基本工况下，当钻孔深度为1 000～2 000 m 时，钻孔每米最大换热功率范围为72～113 W/m。

图4 不同钻孔深度地埋管换热器最大换热功率图

以每米钻孔恒定换热功率为50 W/m 从钻孔取热，地埋管出口水温随时间的变化曲线如图5(a)所示，当钻孔深度分别为1 000、1 200、1 400、1 600、1 800、2 000 m 时，运行2 880 h 后地埋管出水端温度较最初时刻分别下降了11.85、11.65、11.26、10.66、9.85、8.83 ℃，这说明当每米钻孔换热功率一定时，钻孔深度对地埋管出水温降影响不大。以钻孔总恒定换热量100 kW 从岩土层取热时，地埋管出口水温随时间的变化曲线如图5(b)所示，地埋管出水温降会随着钻孔深度的增大(即每米换热功率减小)而逐渐减小。同时，随着深度的增大地埋管出口水温虽逐渐提升，但这种提升的幅度逐渐趋缓。

图5 不同钻孔深度下地埋管出口水温随时间的变化曲线图

当换热功率恒定时，深度每增加200 m，相应的地埋管出口水温升高约2.9 ℃，即等幅度改变钻孔深度时，地埋管出口水温也近似等幅改变，这说明在每米换热功率恒定时钻孔深度与地埋管出口水温近似呈线性影响关系，如图6 所示。

图6 恒定换热功率下不同深度对应的地埋管出口水温图

3.3 地温梯度的影响

地温梯度主要受地质构造等因素影响。不同地区地质情况不同，地温梯度也有一定的差异，由于地温梯度是影响地埋管换热器换热效率的重要因素，因此有必要对其影响程度进行量化分析。以表1 基本参数为例，不同钻孔深度下，不同地温梯度对应的最大换热功率如图7 所示。随着岩土地温梯度的不断增加，中深层地埋管换热器的最大换热功率不断增大。当地温梯度为0.02 ℃/m、钻孔深度为1 000 m时，地埋管换热器最大换热功率仅为57 W/m，当地温梯度为0.04 ℃/m、钻孔深度为2 000 m 时，地埋管换热器最大换热功率可达148 W/m，约为前者的2.6 倍。由此可见，地温梯度对地埋管换热效率的影响不可忽视。当地温梯度为0.020 ～0.040 ℃/m，1 000～2 000 m 地埋管换热器的最大换热功率范围约为57～148 W/m。

图7 不同钻孔深度下地埋管最大换热功率与地温梯度的关系曲线图

当地温梯度为0.020 ℃/m、钻孔深度为2 000 m时，地埋管换热器所对应的地埋管最大换热功率与地温梯度为0.030 ℃/m、钻孔深度为1 200 m 及地温梯度为0.035 ℃/m、钻孔深度为1 000 m 的地埋管换热器所对应的最大换热功率相近，因此在获取相同最大换热功率的条件下选择较大岩土地温梯度的地区可以大大缩短钻孔深度从而减小初投资。

以基本工况为例，连续120 d 以恒定75 W/m换热功率从岩土取热，不同地温梯度的地埋管出口水温随时间的变化如图8 所示。

图8 不同地温梯度下地埋管出口水温随时间的变化曲线图

当地温梯度以0.005 ℃/m的步长依次增大时，地埋管出口水温依次升高约5 ℃，即在等步长改变地温梯度的情况下，地埋管出口水温也近似等幅度改变，这说明地埋管出口水温与地温梯度近似呈现正比的关系，地温梯度较大工况下地埋管出口水温明显高于地温梯度较小的工况。这是因为地温梯度的改变直接影响了岩土温度，进而影响地埋管与周围岩土之间的换热。相同条件下，地温梯度为0.04 ℃/m时的地埋管出口水温约为地温梯度为0.02 ℃/m 时的3 倍，由此可见，地温梯度变化对地埋管出口水温的影响比较明显。

3.4 岩土导热系数的影响

在对地埋管换热性能影响参数的考量中，不同岩土导热系数对整个地埋管系统换热性能的影响也不容忽视。以表1 基本参数为例，不同钻孔深度下，地埋管换热器最大换热功率与岩土导热系数的关系曲线如图9 所示。随着岩土导热系数的增大，中深层地埋管换热器的最大换热功率也随之增大。这是因为增大岩土导热系数相当于增强了岩土与地埋管之间的换热效果，地埋管最大换热功率与岩土导热系数呈正相关影响关系。同样，在岩土导热系数相同的条件下，2 000 m 钻孔深度的地埋管换热器最大换热功率约为1 000 m 深度地埋管换热器最大换热功率的1.5 倍。在岩土导热系数范围为1.5 ～3.0 W/(m·k)时，1 000～2 000 m 钻孔深度的地埋管换热器最大换热功率范围约为53～130 W/m。

图9 不同钻孔深度下地埋管换热器最大换热功率与岩土导热系数的关系曲线图

以基本工况为例，连续120 d 恒定换热功率50 W/m从岩土取热，改变岩土导热系数，地埋管出口水温随时间的变化如图10 所示。

图10 不同岩土导热系数下地埋管出口水温随时间的变化曲线图

岩土导热系数越大，地埋管出口水温越高。但随着岩土导热系数的增大，地埋管出水温度升高的幅度逐渐缓慢。因此，准确获取钻孔周围岩土导热系数对评价地埋管换热效果而言十分关键。

3.5 质量流量的影响

循环液质量流量也是地源热泵研究及设计过程中的一个重要参数。不同质量流量对地埋管换热器最大换热功率的影响如图11 所示。可以看出，地埋管换热器最大换热功率随循环水流量的增大而增大，但增大的趋势越来越慢。质量流量由8 kg/s 增加到10 kg/s，地埋管换热器的最大换热功率提升了约8.6%，而质量流量由14 kg/s 增加到16 kg/s 时，最大换热功率仅提升2.4%。在质量流量为8 ～16 kg/s范围内，2 000 m 钻孔深度的地埋管换热器最大换热功率约为101～123 W/m。