超声波作用下的毛细现象
2022-12-25张天宇邓欣雨陆建隆
张天宇,邓欣雨,陆建隆,王 巍,钟 鸣
(南京师范大学 a.物理科学与技术学院;b.教师教育学院,江苏 南京 210023)
生活中常见的毛细现象是指将细小的玻璃管插入水中,水会在管中上升一定高度的现象. 而超声毛细现象是指将毛细管的一端浸没在超声波浴中,毛细管内的液面出现显著上升的现象,同时液面上升高度通常高于未加超声波时由于毛细现象导致液面上升的高度. 超声毛细现象未来可应用于医学领域制作微型泵装置、或大型压力泵等工业领域. 1981年,N.V.Dezhkunov和P.P.Prokhorenko 对超声毛细现象与润湿性、表面张力、含气量、蒸汽压的关系进行了实验探究并给出了相应解释,提出毛细管底部的空蚀区是导致超声毛细现象的原因[1]. 2004年,N.V.Dezhkunova和T.G.Leightonb在不同振幅大小的超声波作用下,拍摄得到了毛细管底部空蚀区的照片[2],进一步说明了超声空化是导致超声毛细现象的主要原因. 但目前对于超声毛细现象尚存在理论不够完善、影响参量研究较少、缺乏具体相关参量对毛细管内液面上升高度直接影响的实验研究.
本文利用超声空化理论对超声毛细现象进行了解释,探究了超声毛细现象的影响因素,利用一定频率的超声波产生周期性的正压与负压,在毛细管下方激发出大量空化气泡聚集破裂的空蚀区,推动毛细管中液面不断上升,从而产生超声毛细现象. 通过设计实验,探究了声压、温度、毛细管内径等参量对毛细管内液面上升高度的影响,进一步证明了超声空化理论的合理性.
1 超声毛细现象的理论分析
1.1 超声毛细现象的定性解释
根据超声空化理论[1-3],超声毛细现象是由于玻璃毛细管底部机械切割造成大量微裂缝,在超声波作用下这些微裂缝导致在毛细管底部一定区域内存在空蚀云(大量空化气泡的云状聚集区),空蚀云内的大量气泡不断经历生长、收缩、溃灭的空化过程,由于这些空化过程发生的周期非常短[一般为几个超声周期内(0.1 ms内)],从而推动毛细管内液面显著上升.
1.2 超声波声压对超声毛细现象的影响
采用热力学理论,通过导出超声波作用下的单泡空化运动方程(单个气泡半径R与时间t的函数关系),并通过数值模拟,即可推测出超声波的空化阈值.探讨在不同超声波声压下,超声波声压大小对超声毛细现象的影响.未加超声波时,假设初始气泡内部压强为pin,初始气泡外部压强为pout,则未加超声波时,单一气泡内部压强和外部压强的表达式:
pin=pv+pg0,
(1)
(2)
其中,pv为水蒸气压强,pg0为气泡内除水蒸气外其他气体的压强,p0为液体压强,2σ/R0为表面张力带来的附加压强,σ为表面张力系数,R0为气泡初始半径.
根据气泡内外力学平衡可知,初始气泡内部压强等于初始气泡外部压强,即pin=pout,由式(1)~(2)可得气泡内除水蒸气外其他气体压强为
(3)
将声压为pa的超声波声场作用于气泡后,气泡半径由R0变为R,气泡内除水蒸气外其他气体压强由pg0变为pg.此时气泡内外压强变为
pin′=pv+pg,
(4)
(5)
其中,pin′为外加超声波后气泡内部压强,pg为外加超声波后气泡内除水蒸气外其他气体的压强,pout′为外加超声波后气泡外部压强,pa为超声波声压.
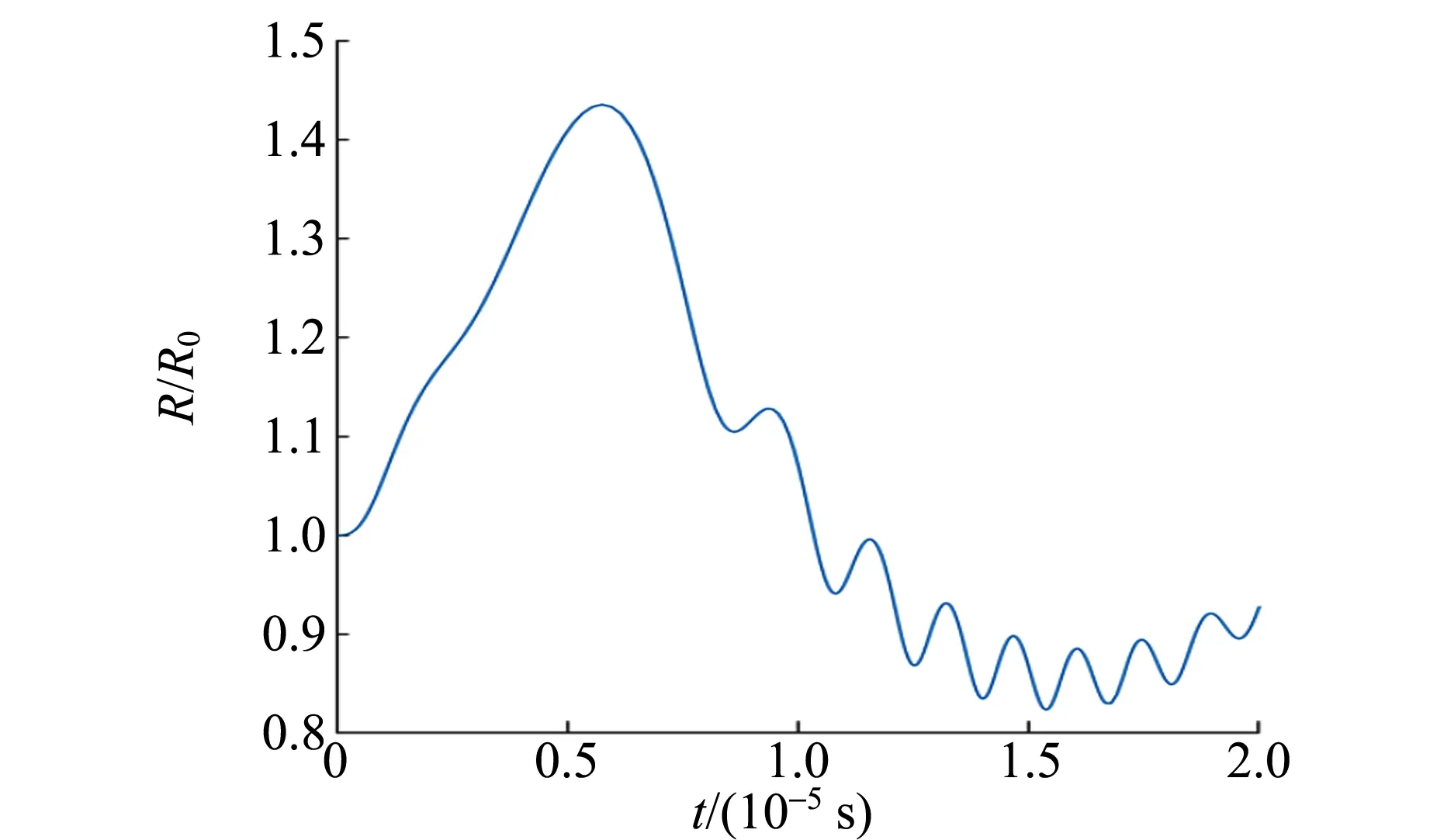
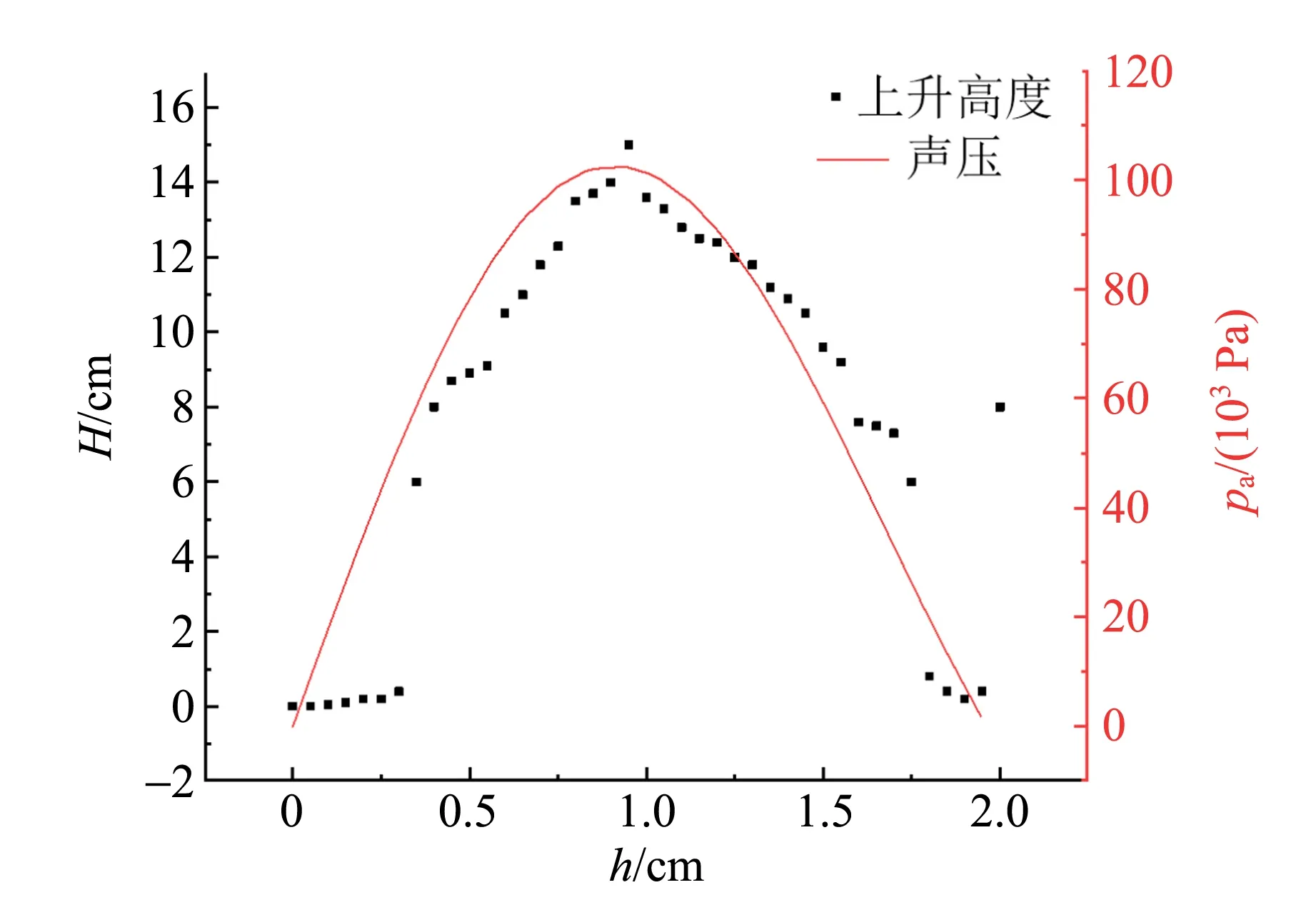
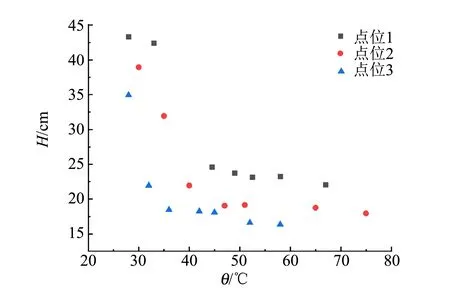
当加超声波后,气泡内部压强大于气泡外部压强,即pin′>pout′时,气泡膨胀;当加超声波后气泡内部压强小于气泡外部压强,即pin′ 假设气泡在施加超声波前、后经历了多方过程[4],则施加超声波后,气泡经历多方过程前后,压强与体积的关系为 pVn=C, (6) 其中,n为绝热系数,C为常量. 根据式(6)可得气泡在施加超声波后,气泡内除水蒸气外其他气体压强pg与未施加超声波时的压强pg0满足如下关系: (7) 其中,R为施加超声波后的气泡半径. 当空化气泡收缩时,周围整个空间的液体将移向气泡收缩所释放的空间,其动能为 (8) 其中,v为液体移动的速度,ρ为液体(水)密度,m为周围液体质量. 液体获得的动能即为气泡受到的外部压力pout′克服内部压力pin′所做的功,具体表示为 (9) 式(9)等号左边为液体移向气泡收缩空间获得的动能;右边为气泡外部压力克服内部压力所做的功.上式两边对R微分后整理得: (10) 将式(4)~(5)代入式(10),得到在不考虑气泡内部蒸汽压的情况下[4]空化气泡的运动方程: (11) 在式(11)的基础上,考虑运动能量的黏滞损耗和声波辐射阻尼,可以得到最终气泡运动表达式[5-6]为 (12) 由式(12)可知,气泡半径随时间的变化与超声波声场的声压振幅pa有关.在不同超声波声压振幅下,气泡半径随时间的变化关系较复杂.因此,使用替换法可将式(12)的二阶常微分方程化简为一阶微分方程组,再利用Matlab进行四阶Runge-Kutta法数值模拟,最后即可得到不同超声波作用下气泡半径比R/R0随时间t的变化图像. 假设气泡经历等温过程[7-8],即n=1,在Matlab仿真中选取的各参量取值如表1所示.实验采用的液体为水,故液体相关参量均取水的参量值.通常情况下,作用到气泡的是正弦或余弦声波,故取超声波声压pa=-pAsin (2πft) Pa,气泡初始半径取值可以参考其他相似文献[4,8],超声频率采用实验仪器的频率,图1为在超声波振幅pA分别为0.7×105Pa,1.0×105Pa和1.5×105Pa的情况下,气泡半径比值随时间的变化图像. 表1 Matlab仿真选取的参量值 由图1可知,气泡半径比值从1开始,随着时间不断增加,在超声波作用下,经历了生长、收缩,最后半径迅速缩小至发生高速溃灭的过程. 超声波作为物质波在水中传播会引起局部区域水分子疏密程度的变化,从而在宏观上呈现出周期性的正压与负压. 气泡在超声波的负压作用下,随着声压逐渐增大,气泡崩溃前R/R0增大,单一气泡的空化剧烈程度随之增加. 不同声压大小下,气泡膨胀的半径比分别为1.4[图1(a)]、2.5[图1(b)]和6.6倍[图1(c)];当超声波的正压作用时,气泡收缩并高速溃灭至半径接近0,此过程中将会释放强大的冲击波,该冲击波引起的高速冲流是毛细管内液面上升的主要因素. (a)pA=0.7×105 Pa 通过Matlab可以进一步得到图2,即气泡崩溃时R/R0与超声波声压p的关系图像. 可以发现:在p<1×105Pa时,气泡溃灭时R/R0的值相对较小;在p>1×105Pa时,R/R0的值迅速增长,说明气泡超声空化现象存在明显的空化阈值. 从图2可以看出表1相应数据下的空化阈值约为1×105Pa. 当声压低于空化阈值,难以发生空化现象;当声压高于空化阈值,气泡超声空化现象的剧烈程度将会随着声压增大而迅速增加. 图2 气泡崩溃时R/R0与p的关系图像 通过以上分析,声压大小是影响单泡空化强度的决定性因素,对超声毛细现象具有重要影响. 在声压大小低于空化阈值时,附加压强小,超声毛细现象难以发生;当声压大小超过超声空化阈值时,声压大小增大,附加压强增加,超声毛细现象随之变得剧烈. 空化气泡运动方程[式(12)]中的参量包含液体的表面张力、黏度、密度等参量,而温度对于水的表面张力、黏度、密度等都有影响,因此温度对超声毛细效应也具有一定影响[1]. 对水而言,温度上升导致水的蒸汽压迅速上升(从20 ℃增加到80 ℃,对应蒸汽压增长20倍),气泡半径虽有一定增长,但是溃灭用时大幅延长,导致单泡空化能量下降,半径对气泡内压力影响变小,部分气泡膨胀过度,在1个压缩相中难以崩溃,气泡崩溃比例下降[1,9],引起超声毛细附加压强下降,从而导致超声毛细现象减弱. 由于在超声毛细现象中,毛细管口的众多微裂缝对空化有着决定性作用,当毛细管内径增大时,单位面积存在的微裂纹数目下降,从而导致空蚀区内空化气泡数密度下降,附加压强减小,超声毛细现象进而减弱. 除了上述讨论的声压、温度和毛细管内径对超声毛细现象有影响外,还有其他因素对超声毛细现象有影响. 根据Blake对空化阈值的结论[10-11],频率对空化阈值没有影响,但随着频率的增大,气泡膨胀时间缩短,气泡不能很好地膨胀,导致超声作用下气泡溃灭时的气泡半径减小;同时过高的频率会大幅缩短气泡压缩时间,导致气泡来不及崩溃而转入下一周期的膨胀,最终使得产生的附加压强减小,超声毛细现象减弱[8,12]. 推荐理由:从科学哲学的根本问题,到科学史上的历史事件和哲学主题,彰显了历史、科学、哲学的无止境魅力。本书化繁为简,剖析根本,纵观西方科学两千年,探讨近代科学发展,它拥有的不仅是知识,更是一套新的认知体系。“如果你每天都读你看得懂的书,你就只知道已知的世界观”。所谓成长,就是用《世界观》升级认知。 液体的含气量是决定空化气泡数量的重要因素,在超声振幅较小时,毛细管端口附近的空化气泡密度随液体含气量的增加而增加,进而能够增大超声毛细现象的剧烈程度;而在超声振幅较大使端口附近的空化泡密度接近饱和时,含气量的增加将会导致气泡内压强增加,其效果与增加蒸汽压相同,会减小附加压强,从而减弱超声毛细现象. 目前,通过脱气、沉降、沸腾等措施均可以改变水的含气量[1]. 如图3所示,实验装置由超声波清洗仪、玻璃毛细管、铁架台、刻度尺组成. 超声波清洗仪提供超声波,铁架台用于固定长玻璃毛细管及调整毛细管入水深度,刻度尺用于测量毛细管内液面高度. 超声波清洗仪选用朗菲的CS-601单源版成品超声波清洗仪,其额定电压12 V,功率24 W,超声频率47 kHz,最大容积0.5 L. 玻璃毛细管为定制的内径为0.4 mm、外径为2.7 mm、长50 cm的石英毛细管. 上下固定装置均为带有2.7 mm孔径的3D打印固定板并通过夹子夹持固定于铁架台上. 图4为实验装置实物图. 图3 实验装置示意图 图4 实验装置实物图 运用COMSOL软件中声学仿真模块,对超声波清洗槽建模,添加压力声学组件并进行超声波振动面的参量设定,对实验选用的超声波清洗仪中的超声波声压场进行有限元仿真,得到如图5~6所示的声压剖面图,声压剖面图即为超声清洗仪内部各处声压与位置之间的关系图. 图中横坐标表示以超声清洗仪中心为坐标原点的长度方向位置,左纵坐标表示宽度方向位置,右纵坐标表示声压大小. 图5为水下2 cm的处声压大小剖面图,图6为超声清洗仪中心对称面处的声压大小剖面图,即装置长度方向中心对称面所在平面. 由图5可见,超声清洗仪的大部分区域(蓝色部分)中声压大小不能达到1×105Pa的超声空化阈值. 图6中的少数区域(长度方向对称面上距中心2 cm处的底部以及仪器正中水下1 cm处)可以得到超过空化阈值的声压大小,此区域应为超声空化现象剧烈地带. 图5 超声清洗仪水下2 cm处声压大小剖面图(图中标注的4个点为局部声压大小的极大值) 图6 超声清洗仪中心对称面处声压大小剖面图(图中标注的4个点为局部声压大小的极大值) 将COMSOL仿真得到的超声清洗仪内水下2 cm处声压仿真剖面图数据导入Origin软件绘制三维图像,如图7所示,沿超声波清洗仪内槽的长边建立x轴,沿超声波泵内槽的短边建立y轴,用(x,y)坐标表示超声波清洗仪内的对应位置,z坐标表示超声波声压大小. 图7中红色框区域为选定的实验区域,即玻璃毛细管放置区. 实验区没有选择中央2个最大的声压区进行实验(对应图7中2个对称红色峰值区域),因为在此区域内的毛细管存在溢出情况,不便于定量探究. 图7 超声波清洗仪水下2 cm处声压与位置关系仿真图 在所取图7红色框区域的实验范围内沿长度和宽度2个方向分别间隔2.5 mm取实验点(在峰值附近取1 mm间隔),并控制内径为0.4 mm的毛细管入水深度2 cm,待毛细管内液面通过一般的毛细现象逐渐上升至稳定位置,打开超声波清洗仪,通过视频拍摄记录在超声波作用下1 min内毛细管内液面所能到达的最高位置,与原先由于毛细现象导致的上升高度相减,得到剔除毛细现象后超声波浴作用于水下2 cm处所取范围内毛细管内液面上升高度的数据,导入Origin绘制三维图像,如图8所示. 图8 超声波清洗仪水下2 cm液面上升高度与位置关系实验图 将图7中红色框区域与图8对比可以看出:图7中的3个声压峰值聚集区域,在图8中同样可以观察到相应的上升高度的峰值. 而在声压模拟分布图像中,在其余声压相对较低的区域,实验所获得的图像中同样没有出现明显的超声毛细现象. 据此可以得出结论:在声压峰值处,超声毛细现象剧烈程度明显高于声压较低处,声压是超声毛细现象的重要影响因素. 为进一步验证声压对超声毛细现象的重要影响,改变毛细管的入水深度,比较同一位置处[平面坐标(0,0)处,声压分布如图6中对称线所示]声压与毛细管内液面上升高度随入水深度的变化. 图9为毛细管内液面上升高度与模拟声压大小分别与入水深度的关系图像,横坐标为毛细管入水深度h,左纵坐标为毛细管内液面上升高度H,右纵坐标为COMSOL模拟得到的声压大小. 观察图9发现:确实存在声压大小的空化阈值. 在声压较低时,毛细管内液面上升高度很小;当声压随入水深度改变而增大到大于空化阈值后,毛细管内液面上升高度与声压随入水深度的变化趋势基本一致,即与声压大小成比例. 上升高度随入水深度的变化相较于声压随入水深度的变化有一定的滞后,其原因可能是超声波在水中超声空化效应而存在一定的衰减,从而导致模拟声压图像整体向入水深度小的方向偏移. 因而可以得出结论:入水深度主要通过影响超声波的声压,间接影响超声毛细现象的剧烈程度,这也进一步证实了声压对超声毛细现象具有重要影响. 图9 上升高度与模拟声压和入水深度的关系图像 为探究温度对超声毛细现象的影响,根据先前声压实验中不同位置处毛细管内液面上升高度的情况,选取了3个位置,即超声毛细现象较强而又恰好不导致毛细管内的水柱溢出毛细管现象,选取入水深度2 cm的3个点位,水平位置分别为:点位1(4.75,-2)、点位2(5,1.75)、点位3(6.25,0),并选取70 ℃的温度为起始点,进行实验. 通过水的自然冷却降温以部分抵消因超声波能量耗散导致的水温上升,并严格控制毛细管内液面上升高度,保证测量过程中的前后水温相差不超过1 ℃,得到如图10所示结果. 图10 3个不同点位处不同水温对应的毛细管内液面上升高度 图10中不同颜色点代表了不同的取点位置,分析不同取点位置温度与毛细管内液面上升高度的关系存在共性:毛细管内液面上升高度在30~40 ℃之间随温度上升迅速下降,在40 ℃之后随温度上升缓慢下降. 根据超声空化理论的解释为温度的上升减小了空化气泡的能量,升高了空化区气泡的空化阈值,从而导致液面上升高度在降温前段迅速下降,在降温后段缓慢下降. 因此在实验选取的温度范围内,实验结果验证了温度对毛细管内液面上升高度影响的理论分析,即一定温度范围内超声毛细现象与温度呈负相关. 选用内径分别为0.3,0.4,0.5,1.0 mm的毛细管,进行毛细超声现象的实验,为避免溢出,在声压较弱的同一点位进行不同内径的对照实验,得到如图11所示的实验结果. 可以看出,毛细管内径越大,液面上升高度越低. 由于理论分析中毛细管口周长与管口面积之比随半径增大而反比例减小,因此采用反比例函数拟合数据点,实验结果与理论相符,在一定程度上进一步验证了超声空化理论对毛细管内径影响因素分析的正确性. 图11 毛细管内液面上升高度与毛细管内径的关系图 本文选用超声空化理论对超声毛细现象进行了解释,利用Matlab计算得到单一空化气泡运动方程,并研究了声压对单泡空化气泡运动破裂强度的影响,通过超声空化理论分析了相关参量对超声毛细现象的影响. 研究表明:声压是影响超声毛细现象的重要因素,只有声压高于某一阈值时,超声毛细现象明显,且声压大小与液面上升高度呈正相关;在实验范围内(30~75 ℃),温度与超声毛细现象剧烈程度呈负相关,在30~40 ℃之间迅速下降,在40 ℃之后缓慢下降;毛细管内径与超声毛细现象呈负相关.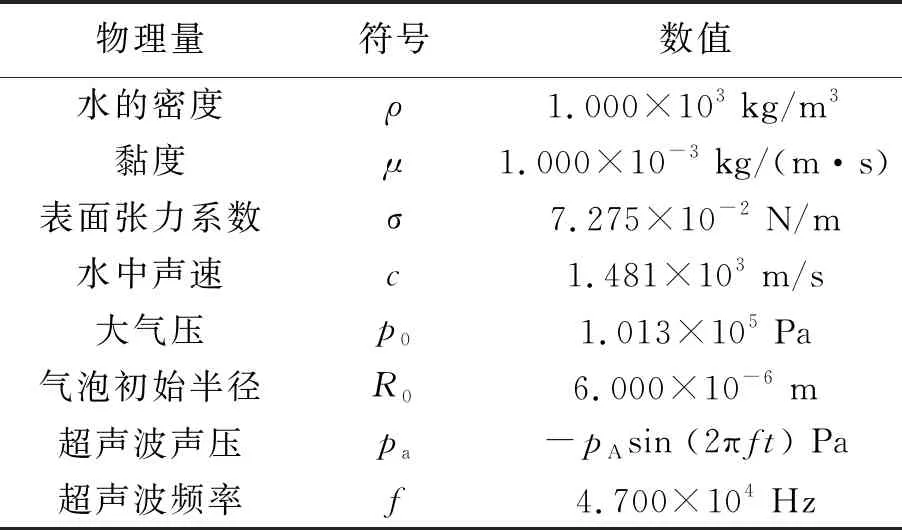
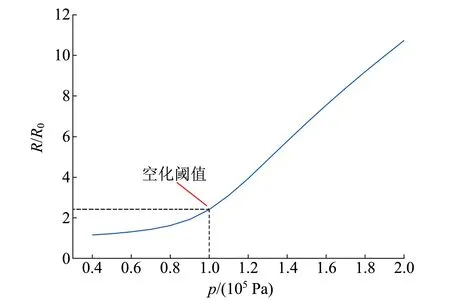
1.3 温度和毛细管内径对超声毛细现象的影响
1.4 其他因素对超声毛细现象的影响
2 实验探究
2.1 实验装置
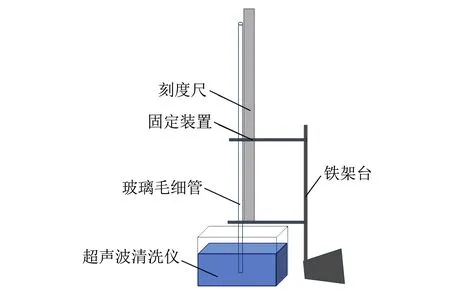

2.2 仿真超声波清洗仪声场声压分布
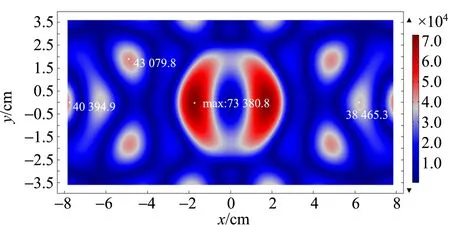
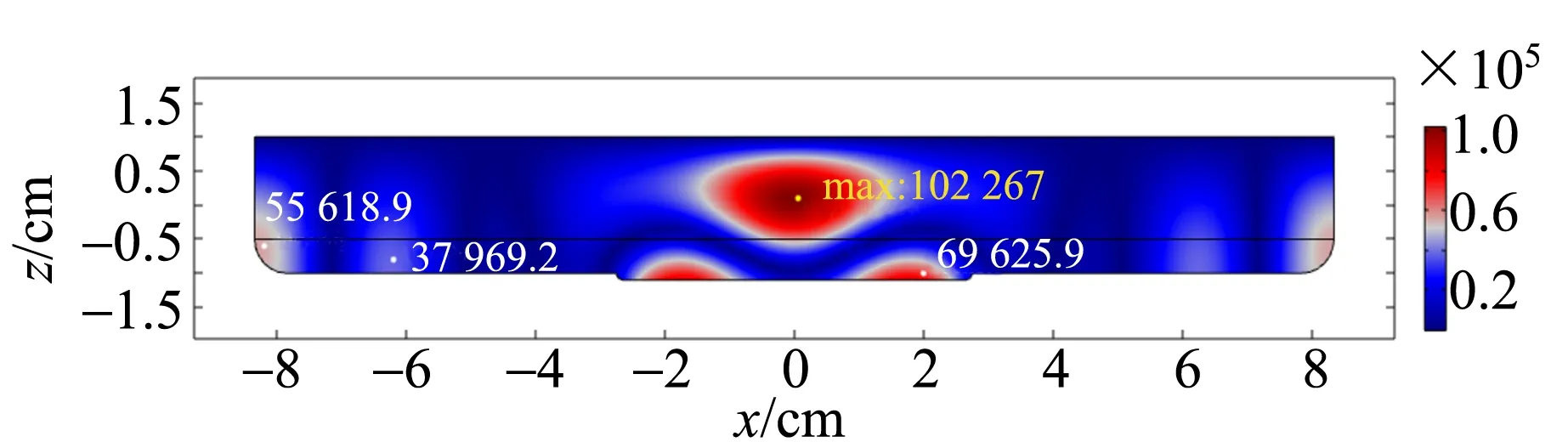
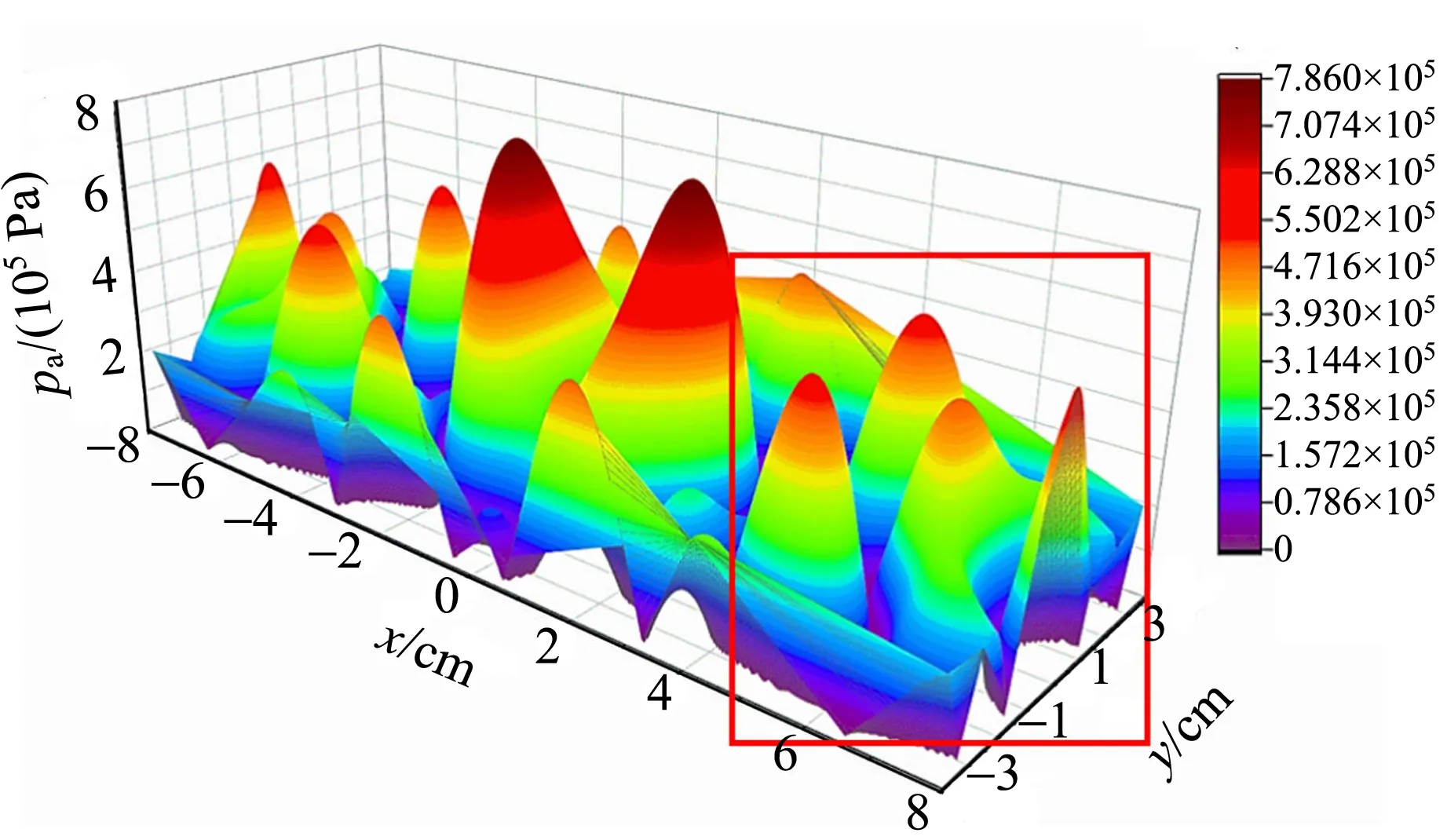
2.3 探究声压与毛细管内液面的上升高度关系
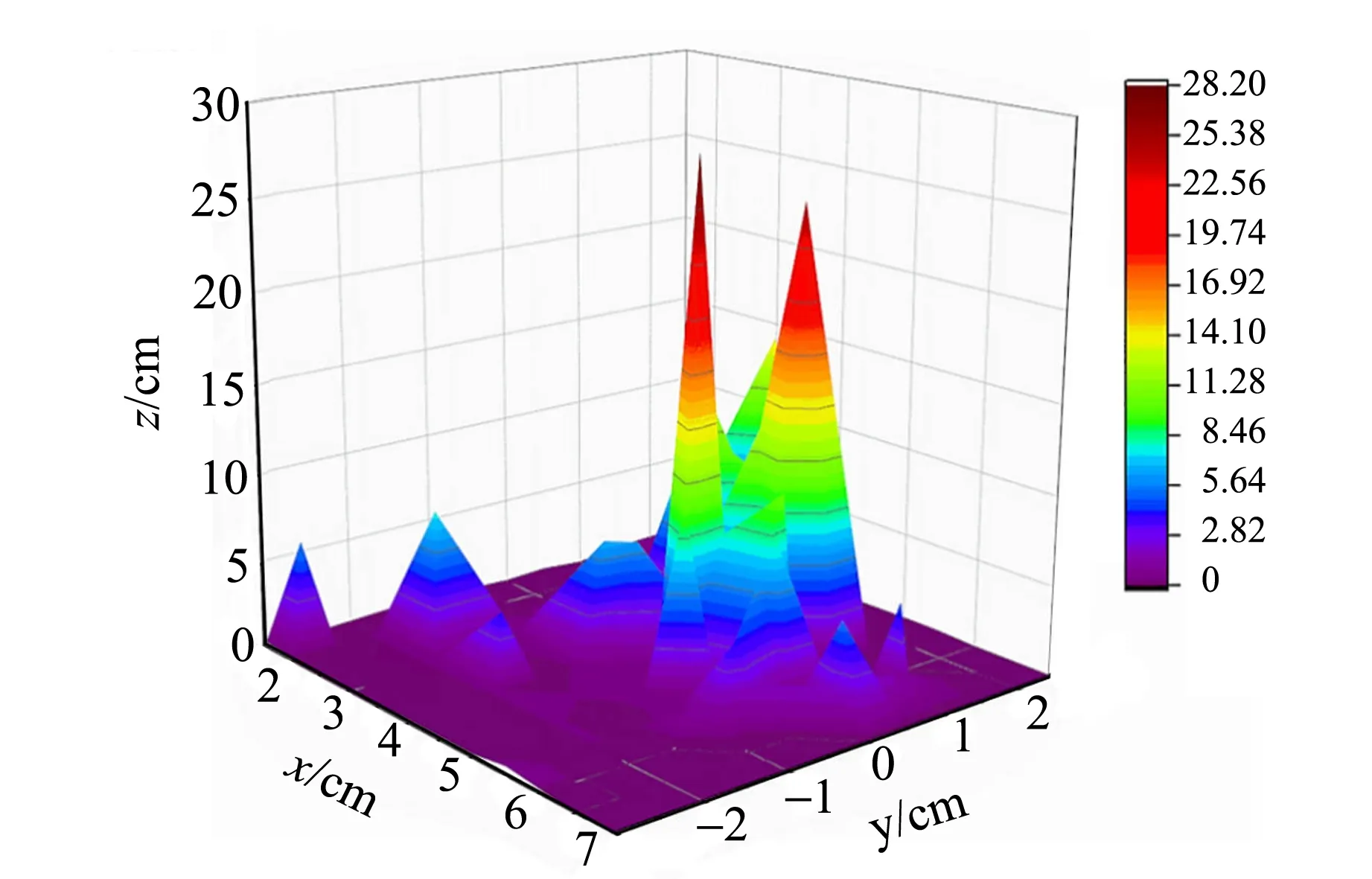
2.4 温度与毛细管内液面上升高度的关系
2.5 毛细管内径与液面上升高度的关系

3 结 论
