空间平台发射拦截器动力学与最优脉冲拦截

韩艳铧，王 磊，张 勇

（1.南京航空航天大学航天学院，南京 211106；2.南京航空航天大学无人机研究院，南京 210016）

空间拦截在空天防御、在轨服务、太空碎片清除等领域意义重大，是空间技术领域持续热门课题。脉冲法制导，因其原理和算法相对简单，易于工程实现，当轨控推力作用时间远小于惯性滑行时间时，制导误差很小，因此在空间拦截领域颇受重视［1⁃6］。空间拦截任务中，燃料和时间均是宝贵资源，因此文献［1⁃2］采用非线性规划方法对脉冲控制进行优化，文献［3］基于轨道力学中的普适变量描述法，采用内外双循环的穷举搜索，对脉冲拦截控制进行优化。文献［4］为了减少拦截造成的空间污染，降低能量消耗，提高拦截概率，提出了停泊轨道转移逆轨网捕拦截的方式。Lawden［7］提出的主矢量方法是航天最优控制领域的经典方法。通过对主矢量特性的分析，可以快速找到最优脉冲的作用时机和方向［8⁃10］。其中文献［8］采用主矢量方法，研究了从地球（行星）或月球表面发射火箭拦截圆形环绕轨道上目标星的脉冲最优控制问题，拦截时间固定，燃耗为性能指标，但是未考虑大气影响。文献［9］考虑追踪星和目标星近距离相对运动，满足C⁃W 方程，追踪星采用脉冲制导，用主矢量法确定最优脉冲施加时机、大小和方向。文献［11］针对目标星处于椭圆轨道且追踪星与目标星近距离相对飞行的情况，研究了时间最省切向脉冲拦截问题，采用遗传⁃序列二次规划相结合的方法克服了优化解对迭代初值的敏感性。考虑到若发动机推力较小，采用脉冲法计算的制导律在实际应用中会产生较大误差，文献［12］受脉冲法启发，将拦截途中每个控制采样时刻当作初始时刻，用最优脉冲制导算法给出当前时刻应施加在拦截器上的发动机推力方向，如此不断迭代，直至拦截到目标，该方法的拦截精度可以保证，但总体上已不具有最优性。无论是脉冲制导还是连续推力制导，凡涉及最优策略往往计算量较大，难以在线实现，基于小参数摄动的近似优化拦截在航天领域应用而生［13⁃14］，以较小的性能牺牲为代价，大大减轻计算负担，可用于在线拦截制导。

本文研究平台携载拦截器，与目标星形成绕飞关系。绕飞过程中平台的姿控系统维持其发射筒轴线始终瞄准目标星。拦截器从发射筒分离后，自身的小型火箭发动机给其施加一个速度脉冲，修正其飞行方向，然后拦截器凭惯性飞向目标星，如图1 所示。

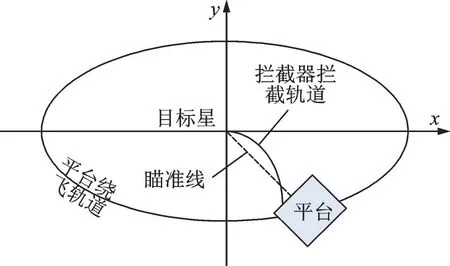
图1 平台绕飞并瞄准目标星示意图Fig.1 Sketch of the platform flying around and aiming at the target satellite

图2 给出了拦截器在平台中的装载几何关系，拦截器在其中形成一个矩阵。为了直观表示拦截器的发射方向，图中的拦截器头部用锥头表示。拦截器只能被依次发射，即平台不能同时发射两枚以上拦截器。拦截器可通过平台中的电磁或气压装置发射。

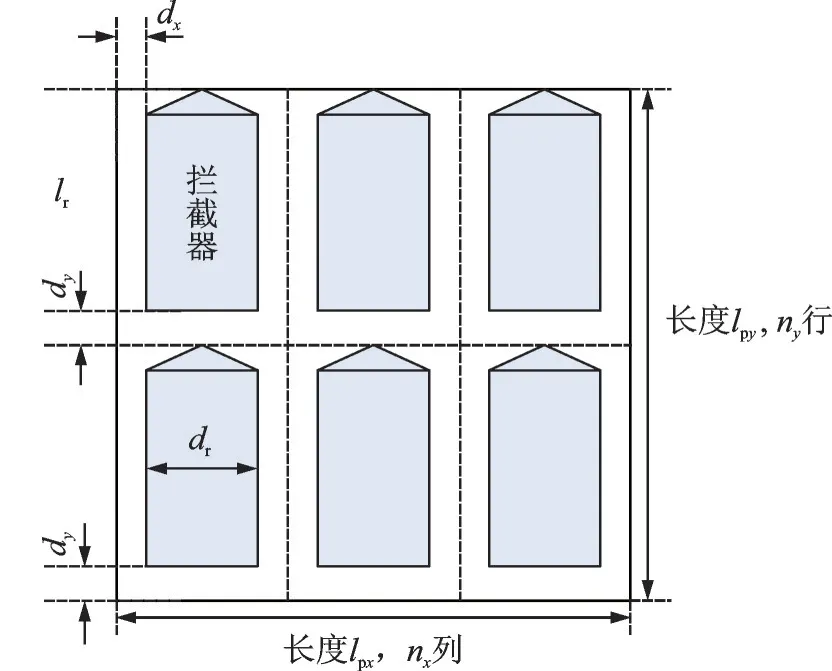
图2 平台携载拦截器示意图Fig.2 Sketch of platform carrying interceptor

文本采用小参数正则摄动方法，快速求解出燃耗最省最优脉冲的一阶近似解，该值接近最优解，以此为迭代初值，用非线性规划方法可以快速可靠地收敛到最优真解。

1 发射过程平台‑拦截器两体动力学

首先建立目标星轨道坐标系oAxAyA，该坐标系的原点固定于目标星，xA轴正方向沿着目标星绕地速度方向，yA轴垂直于xA轴且背离地心方向为正。再建立平台本体系oBxByB，其原点在平台质心，yB轴沿平台上的发射筒轴线方向，且以发射方向为正，xB轴垂直于yB轴，且在图2 中向右为正。以上两坐标系在下文中分别简称为A 系和B 系。

以目标星轨道坐标系的yA轴表示平台姿态偏航角的参考方向，且以右手规则定义偏航角的正负，在图1 和2 中即逆时针偏航为正。

设任何一个矢量v在两坐标系的投影列阵分别为vA和vB，则两者之间的坐标变换关系为

其中坐标变换矩阵

式中η为平台的姿态偏航角。

A 系以角速度n旋转，其中n是目标星绕地圆轨道的角速度（也是平台绕飞目标星的平均角速度），故其严格来说是非惯性系。但是在建立平台发射拦截器的动力学方程时，因为拦截器发射过程耗时与A 系的旋转周期T=2π/n相比是很小的数，或等价地说，该非惯性系的旋转角速度n很小，可视A 系为惯性系，由此引起的建模误差极小。

设平台质心相对于A 系原点的位矢为

式中：右下角标ld 表示“左下”，右上角标p 表示“相对于平台质心”，右下角标B 表示“投影到B 系下”。后文采用类似的表达，不再逐一解释。

本文定义处于平台左下位置的拦截器为第1列1 行，拦截器所在列数的递增方向是从左向右，行数的递增方向是从下向上。

设第i列j行的拦截器固定在平台上，由图2 所示几何关系，知其质心相对于平台左下角的位矢为

第i列j行的拦截器质心相对于A 系原点的位矢

是平台姿态偏航角速率。

第u列w行的拦截器正在发射筒里处于发射滑行状态，设其滑行位移为s，则其质心相对于平台左下角的位矢为

式中

拉格朗日分析力学特别适合多体复杂航天器的力学建模［15］，本文拦截器在发射出筒过程中与平台形成两体耦合系统，拟采用拉格朗日第二类方程建模。

平台动能

2 拦截器拦截目标星最优脉冲控制

当目标星在绕地圆轨道上且追踪星与其距离较近时，追踪星相对于目标星的运动满足C⁃W方程

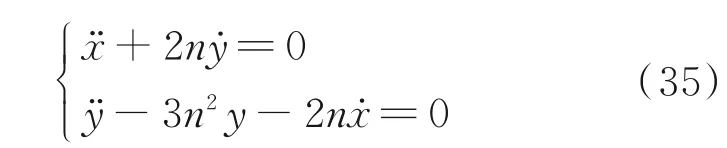
该方程是在目标星轨道系即A 系建立的，其中n是目标星绕地圆轨道的角速度，如果追踪星与目标星形成绕飞关系，n也是追踪星环绕目标星的平均角速度。

式（35）的解析解为

本文的任务是，寻求施加给拦截器的速度脉冲(Δvx0，Δvy0)，使在某时刻tf拦截器能够拦截到目标星，且所需施加的速度脉冲幅值最小，即燃耗最省。

用最优控制语言描述，即

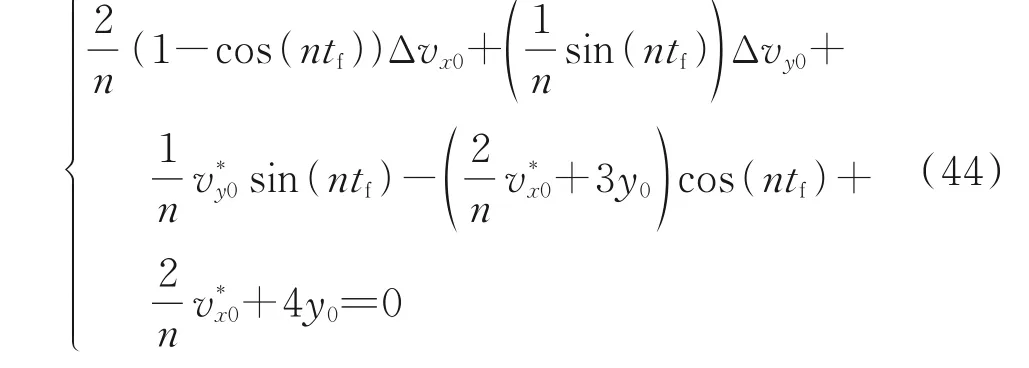
对于非线性规划问题，无论用直接法迭代寻优，还是用间接法，即求解表示最优必要条件的非线性方程组（44），均涉及迭代初值的选取，而初值选取是困难的，尤其是拉格朗日乘子μ1、μ2本身物理意义不明确，迭代初值的确定更困难。迭代收敛过程对迭代初值非常敏感，容易导致计算失败。

本文给出一种求解策略，可谓之“三级优化”，基本步骤如下：

步骤2 将原问题最优必要条件在零阶解附近取一阶摄动，得到一组关于δΔvx0、δΔvy0、δtf、δμ1、δμ2的线性方程。将前述零阶近似解加上述摄动量，得到原最优问题的一阶近似解，即

代入式（46）描述的性能指标得

式（46）描述的零阶近似优化问题的一阶必要条件形式上同式（43），不再重复列写，展开后得

最后一步不详细阐述，以上述一阶近似解作为原优化问题的迭代初值，此值接近真实最优解，故采用任何一种成熟的非线性规划算法均能可靠且快速地收敛到真解。

上述三级优化过程的流程图如图3 所示。

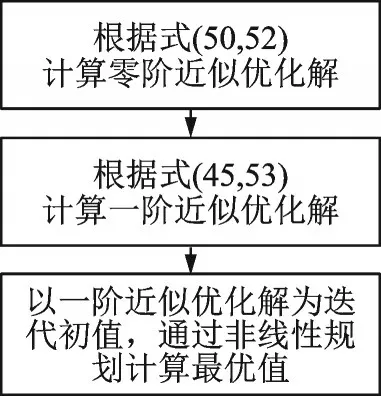
图3 三级优化流程图Fig.3 Flow chart of three⁃level optimization

3 数值仿真

仿真入口参数如表1 所示。

表1 仿真入口参数Table 1 Input parameters for simulation

不失一般性，本仿真以图2 中发射第1 列第2行拦截器为例。仿真结果分别如图4～12 所示。

图4～7 中的红色点划线表示假设平台未发射拦截器，正常围绕目标星做相对椭圆运动，并且时刻保持发射筒轴线瞄准目标星时的运动情况，图中称其为“原始未受扰”运动状态。蓝色实线表示平台发射拦截器，两体相互干扰下的实际运动状态。

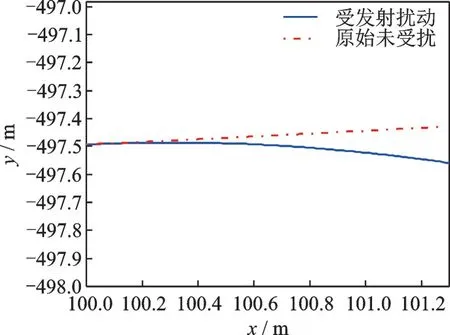
图4 发射过程平台运动轨迹Fig.4 Platform movement trajectory during launch

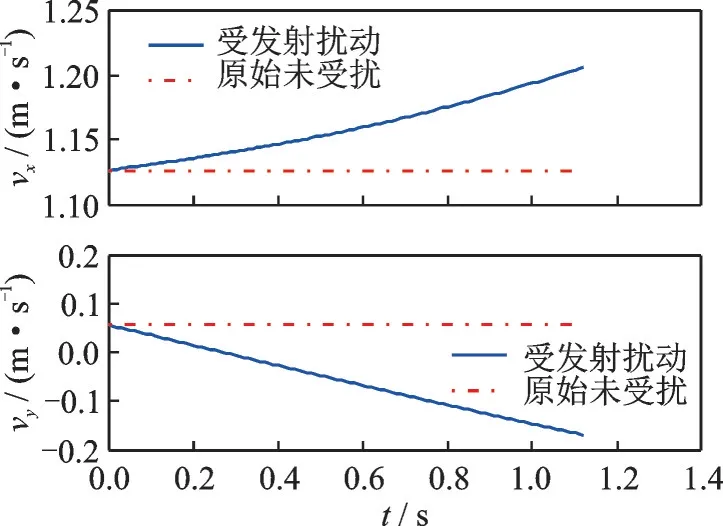
图5 发射过程平台速度的变化Fig.5 Variation in platform velocity during launch

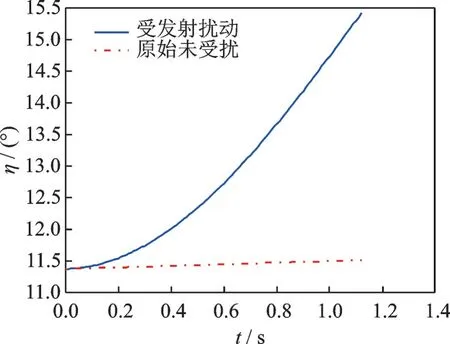
图6 发射过程平台姿态偏航角Fig.6 Platform attitude yaw angle during launch

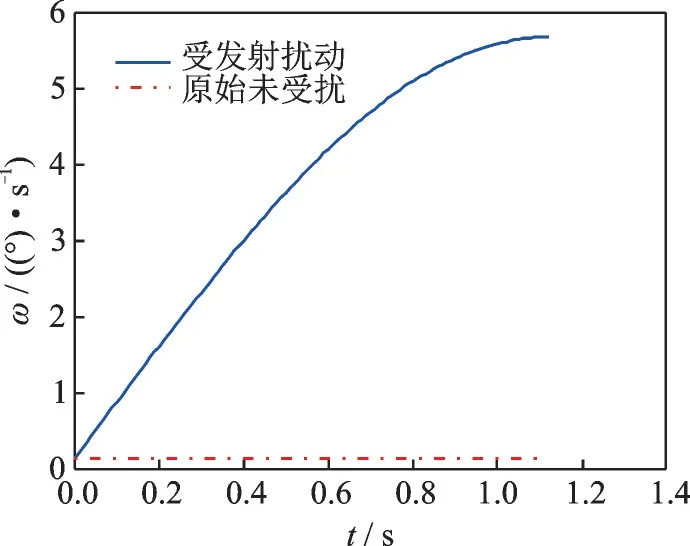
图7 发射过程平台姿态偏航角速率Fig.7 Platform attitude yaw rate during launch

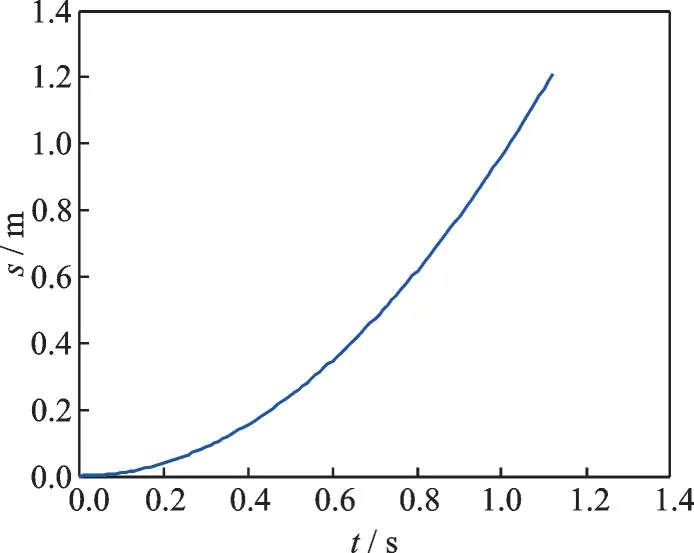
图8 拦截器在平台发射筒中的滑行位移Fig.8 Sliding displacement of the interceptor in the plat⁃form launch tube

图9 拦截器在平台发射筒中的滑行速率Fig.9 Sliding rate of the interceptor in the platform launch tube

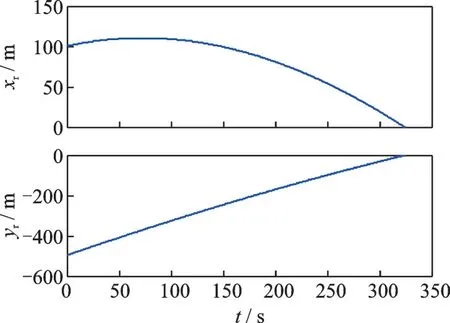
图10 拦截器分离后在拦截轨道上的位置坐标Fig.10 Position coordinates of the interceptor on the inter⁃cepting orbit after separation

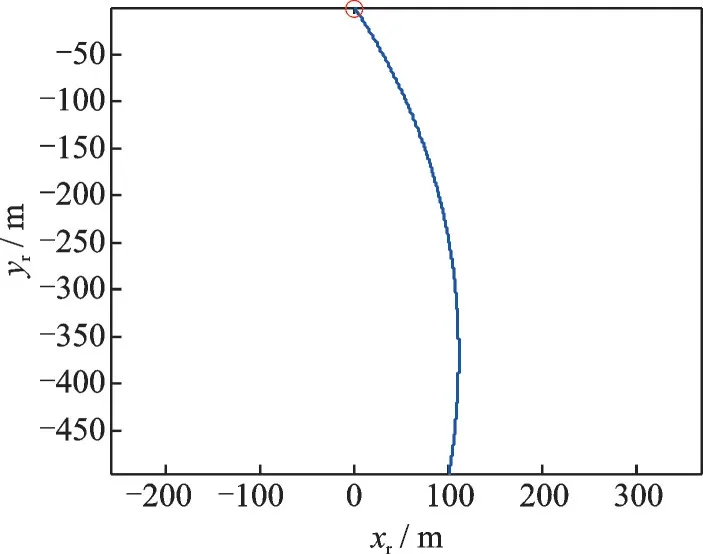
图11 拦截器分离后的拦截轨道Fig.11 Intercepting orbit after interceptor separation

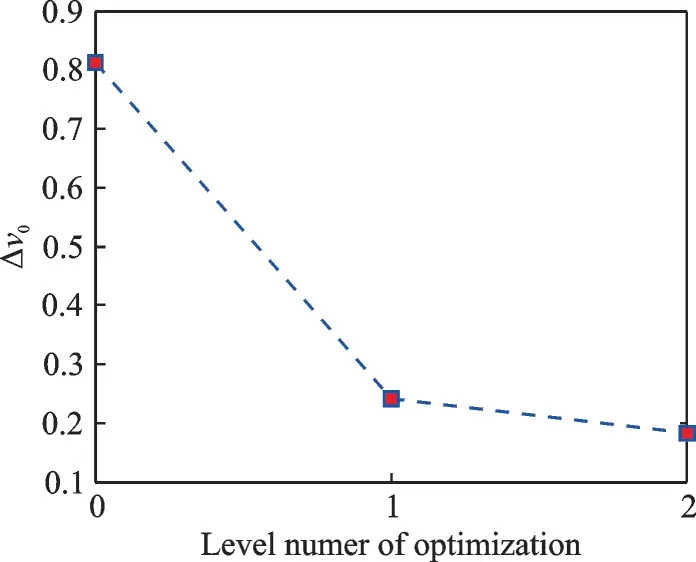
图12 三级优化结果变化Fig.12 Three⁃level optimization results

图4～7 显示，由于发射过程拦截器对平台的反作用力，在拦截器分离瞬间，平台的实际轨迹相对于未受扰的绕飞轨迹沿y轴负方向偏离了约0.13 m，平台的x轴向相对速度增加了0.08 m/s，y轴向相对速度减小了0.22 m/s，姿态偏航角增加了3.90o，姿态偏航角速率增加了5.55 (°)/s。考虑到平台相对于目标星的环绕椭圆的几何尺度和相对环绕速度，可以认为拦截器发射过程对平台的位置坐标影响甚微，但是对平台绕飞速度以及姿态的影响不容忽视。

最后补充说明，本文算出的toptimf/T=0.059 ≪1，说明文中将n视作小参数，采用小参数正则摄动的方法计算一阶近似最优解的前置条件是成立的。

4 结 论

本文针对空间平台绕飞目标星，并发射拦截器来拦截目标星的动力学与脉冲最优控制问题开展研究。在平台与目标星已形成绕飞关系的条件下，拦截器从平台中射出，分离瞬间给其施加一个速度脉冲修正其飞行方向，然后拦截器在C⁃W 方程支配下凭惯性飞行，直至拦截目标星。本文采用拉格朗日第二类方程建立了平台发射拦截器过程的两体耦合动力学，然后采用基于小参数正则摄动的方法给出了最优速度脉冲的一阶近似优化解，并以此为迭代初值，采用非线性规划方法算得最省燃耗最优速度脉冲值，本文谓之“三级优化方法”。最后用数值仿真验证了本文所提方法的有效性。