基于终端滑模的打击时间与打击角度约束制导律
2022-12-25郝文欣王鹏宇朱东方李传江
郝文欣,宋 斌,王鹏宇,朱东方,李传江
(1.哈尔滨工业大学航天学院,哈尔滨 150001;2.上海宇航系统工程研究所,上海 201108;3.上海航天控制技术研究所,上海 201109)
随着反导技术的飞速发展,世界各国逐渐形成一体化的防御体系。日益复杂的战场环境对导弹的杀伤能力和突防能力都提出了更高要求,使得仅考虑零脱靶量约束的制导律难以满足现代战争的需要。研究满足多约束条件的末段制导方法对于在复杂战场环境中提高导弹的作战效能具有重要意义。
现代制导任务通常要求导弹以特定的角度打击目标的薄弱环节,从而获得最佳打击效果。因此,具有打击角度约束的制导律受到广泛的关注。Kim 等[1]在传统比例制导律的基础上,通过增加时变偏置项,使导弹以期望角度击中目标。文献[2]基于线性二次型最优控制提出了导弹任意阶动态模型的最优制导律,通过对剩余飞行时间进行估计,实现了打击角度的约束。文献[3]提出了一种满足打击角度和加速度约束的滑模制导律,通过在滑模面函数中引入阻尼项和设计多幂次自适应趋近律,解决了制导初期产生的指令极值问题。此外,为了突破现代舰船的近程防御武器系统(Close⁃in⁃weapon system,CIWS),制导任务通常需要多枚导弹采用协同制导的方式对目标实施饱和攻击,这对导弹打击时间的控制提出了要求。Jeon 等[4]首先将打击时间反馈误差与比例制导律相结合,通过合理选取比例制导系数使制导律满足打击时间的约束。考虑导引头探测盲区的问题,文献[5]利用虚拟目标将制导过程分为2 个阶段,第1阶段采用圆弧跟踪制导律使加速度指令收敛于零,第2 阶段在无控制输入的前提下以期望打击时间击中目标。Hu 等[6]将导弹的视线角速率设计成含有可调参数的时变多项式,并使用终端滑模控制方法对其进行跟踪,从而建立了打击时间约束制导律。
相较于单约束制导律,同时考虑打击角度与打击时间约束的制导方法将二者的优势结合,具有更重要的战略意义。近年来针对这类问题的研究方法大致分为比例导引律、最优制导律及滑模制导律等[7⁃22]。Lee 等[7]首先对满足打击角度和打击时间约束的制导律进行研究,提出了包含偏置项和反馈环节的最优制导律。Zhang 等[8]将剩余飞行时间期望值与估计值之间的误差引入闭环反馈,设计了包含两个修正环节的比例制导律,该制导律满足打击角度和打击时间的约束。文献[9]基于非线性最优控制设计了前置角的多阶段控制策略,并最终给出了视场受限条件下的打击角度和打击时间约束制导律。与比例控制律和最优控制律相比,滑模控制律因其非线性特性、快速收敛性和强鲁棒性等优势,已经被大量应用于单约束制导律[3,6]和多约束制导律[10⁃16]的设计中。特别地,终端滑模具有使系统状态在指定时间内收敛于零的特性,在考虑打击时间的制导问题(包括同时考虑打击角度和打击时间的制导问题)中被广泛使用。Harl 等[10]将导弹的视线角设计成一个含有可变参数的多项式,并借助边界初值条件和数值循环方法完成多项式参数的求解,从而建立了打击时间和打击角度滑模制导律。文献[11]设计了一种含有两个未知参数的时变滑模面,两个参数分别用来实现打击角度和打击时间约束。文献[12]提出了一种不需要数值解算方法的打击时间与打击角度约束滑模制导律。文献[13⁃16]基于滑模控制对打击角度和打击时间制导律进行更深入的研究。
综合来看,现有文献所提出的制导方法按照是否需要估计剩余飞行时间分为2 类。第1 类方法基于小角度假设和简化的线性模型,将估计的剩余飞行时间与期望值的误差引入闭环反馈。该类方法对估算的准确性要求较高,当导弹飞行轨迹高度弯曲、小角度假设不成立时难以完成制导任务。第2 类方法无需估计剩余飞行时间。例如,文献[10]通过设计制导律使导弹跟踪一个多项式以满足终端约束,使其避免了对剩余飞行时间的估计。但不足之处在于,仍需借助数值运算合理选择多项式的参数。文献[22]基于渐开线制导法将弹目的运动学方程转换至弧长域空间,而后提出了一种打击角度和打击时间分段制导律。文献[23]首先利用一阶泰勒展开将导弹⁃目标模型线性化,而后使用模型预测控制方法设计打击时间和打击角度制导律。
基于上述分析,本文提出一种非奇异终端滑模制导律,可以同时满足零脱靶距离、零终端加速度、打击时间和打击角度的约束。首先将视线角误差参考轨迹设计成带有剩余飞行时间项的时间多项式,而后设计制导律对其进行跟踪。视线角误差参考轨迹多项式含有一个可调参数,通过在线优化过程确定可调参数的值以满足期望的打击时间。需要强调的是,即使在拦截匀速运动目标的情况下,本文设计的制导律也不需要估计剩余飞行时间和预测碰撞点。最后,通过仿真验证所提方法的有效性。
1 问题描述
在二维惯性坐标系OXY下建立导弹与目标的拦截模型,如图1 所示。记M 和T 分别表示导弹和目标,r表示导弹与目标之间的相对距离,λ表示导弹与目标的视线角,VM和VT分别表示导弹和目标的速度,σM和γM分别表示导弹的前置角和弹道角,σT和γT分别为目标的前置角和弹道角,AM表示导弹的加速度,并与VM始终垂直。导弹⁃目标运动关系如图1 所示。
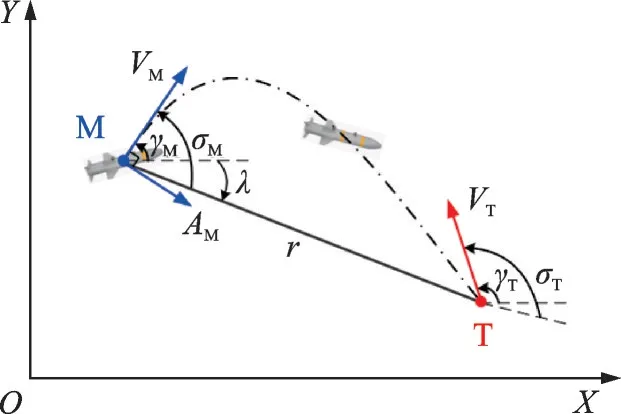
图1 导弹⁃目标运动关系Fig.1 Engagement geometry
假设导弹自动驾驶仪具有理想特性,导弹和目标的速度大小均为常数。根据几何关系,建立导弹与目标的相对运动方程
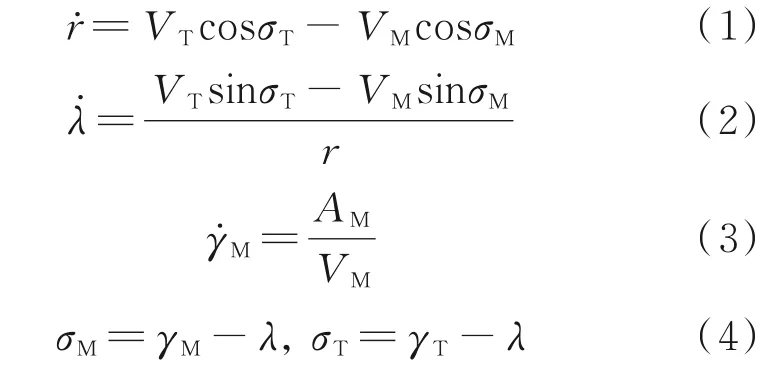
分别用t和td表示导弹发射后经过的时间和期望打击时间,则剩余飞行时间tgo定义为

随着导弹发射时间t趋近于期望打击时间,剩余飞行时间tgo趋近于零。导弹的打击角度一般定义为末制导结束前导弹与目标速度矢量之间的夹角[24]。对于非机动目标,打击角度的约束问题可以转化为视线角的约束问题[25]。不失一般性,本文将打击角度约束定义为终端视线角约束,则制导律的设计目标是在期望的打击角度λd和打击时间td约束下实现零脱靶距离。制导目标可表示为
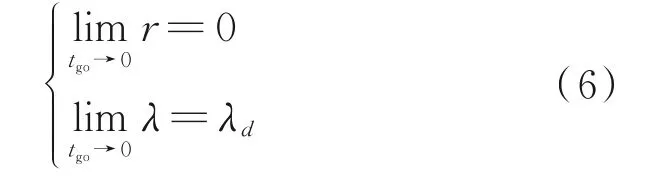
根据上述分析,本文需要设计满足式(6)的制导律以满足打击角度和打击时间的约束。
2 非奇异终端滑模制导律设计
本文设计的具有打击角度与打击时间约束制导方法由以下2 步完成:(1)视线角误差参考轨迹的构造;(2)非奇异终端滑模制导律的设计。本节首先考虑匀速运动目标,将视线角误差参考轨迹设计成带有一个未知参数的时间多项式,该多项式随着时间项趋近于0 而满足打击角度的约束。然后,设计一种非奇异终端滑模制导律跟踪视线角误差参考轨迹。最后基于数值求解方法确定合适的未知参数以满足打击时间约束。
2.1 视线角误差参考轨迹设计
文献[10,16]设计了视线角的参考轨迹多项式,并通过边界条件确定多项式的系数。本文对视线角误差的参考轨迹进行设计,定义视线角误差如下

式中λe表示实时的视线角λ与期望打击角度λd之间的差值。由运动学方程(2),可得λe的一阶时间导数和二阶时间导数
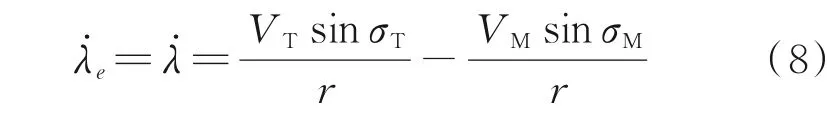

注释1针对运动目标,文献[10]将视线角参考轨迹设计成以导弹水平位置为自变量的多项式,通过终端约束条件确定未知参数的值以满足打击角度和打击时间的约束。本文则直接对视线角误差参考轨迹进行设计,并引入tgo作为多项式的自变量。与文献[10]相比,式(13)随着tgo趋近于0,λeD及其一阶导数也自动收敛于0。根据准平行接近法则,弹目视线角速率在末制导结束前收敛于0或0 附近,导弹即成功击中目标,故而无需再引入终端约束条件。因此,相比于文献[10]在制导律中引入5 个未知参数,本文所提出的方法仅需要3 个未知参数,表达形式更简洁。
注释2如式(13)所示,若设计的制导律令视线角误差λe严格跟踪λeD,则随着tgo趋近于零,λ收敛于λd,制导律满足终端角度约束。式中包含一个未知参数δ1,用于设计打击时间。故而只需考虑制导律以及优化过程的设计,不需要对tgo进行估计。
2.2 非奇异终端滑模制导律设计
由2.1 节分析可知:视线角误差参考轨迹λeD满足打击时间和打击角度约束。因此只需设计制导律跟踪λeD即可完成打击时间和打击角度控制。本小节基于固定时间稳定引理[26]设计一种非奇异终端滑模制导律,并构造Lyapunov 函数对闭环系统的稳定性进行分析。为方便制导律设计,首先定义误差eλ以及终端滑模面如下


选 取 系 统 误 差eλ及 其 一 阶 导 数ėλ作 为 二 阶 系统{eλ,ėλ}的状态变量,则所设计的非奇异终端滑模制导律能够令二阶系统{eλ,ėλ}在固定时间内镇定。
注释3 本文选取系统误差eλ作为二阶系统{eλ,ėλ}的状态变量,则制导律设计目标是令二阶系统状态在固定时间收敛至0。此时视线角轨迹λe严格跟踪视线角误差参考轨迹λeD,即可完成打击角度和打击时间控制。
注释4 为了避免控制器uf产生奇异,制导律引入如式(17)所示的饱和函数。考虑式(18)中p1∈(0.5,1),当ėλ≠0 且eλ→0 时,uf→∞。此时饱和函数能够避免控制器出现奇异,且umax的选取与滑模面在状态空间的位置有关,即umax>0。此外,用饱和函数sat(⋅)代替符号函数sgn(⋅)可有效消除滑模控制律产生的抖振现象。
下面给出定理1 的证明。
证明 由误差构成的二阶系统{eλ,ėλ}在固定时间镇定的证明过程如下。
首先证明系统状态{eλ,ėλ}在固定时间到达滑模面;而后沿着滑模面在固定时间内收敛至平衡点。
如前所述,当sλ≠0 且eλ→0 时控制器uf产生奇异。而当sλ=0时,将式(15)代入式(18)可得控制器uf=α1p1(-α1sig(eλ)(2p1-1)-β1sig(eλ)(p1+g1-1)),由p1∈(0.5,1)可知此时控制器不产生奇异。故而控制器奇异只发生在系统状态到达滑模面之前,即sλ≠0。为方便证明,根据控制器是否达到饱和函数阈值将状态空间划分两个子空间A和B。子空间A、B以及滑模面的位置关系如图2 所示,显然奇异点只出现在子空间B中。A和B的定义如下

图2 系统状态相平面图Fig.2 Phase plane of the control system

式(21)符合文献[26]的固定时间引理。因此二阶系统{eλ,ėλ}在不进入区域B的前提下,能够在固定时间T1内收敛至滑模面sλ=0 上,T1满足如下表达式

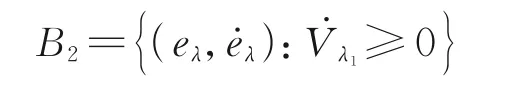
当系统状态由A进入B区域时,饱和函数由sat(uf) =α1p1|eλ|(p1-1)ėλ转 变 为 sat(uf) =sgn(ėλ)umax。由 式(23)可 知V̇λ1不 会 立 即 改 变 符号,在B1区域仍有V̇λ1<0。当系统状态由B1区域进 入B2区 域 后,由p1∈(0.5,1)可 知 若ėλ≠0 且eλ→0 有

如图2 所示,当系统状态进入子空间B2时,eλ→0。跟 据ėλ的 符 号 存 在 以 下2 种 情 况:若ėλ>0,则eλ单调递增,系统状态将沿顺时针方向穿越B2区域到达滑模面sλ=0 上;若ėλ<0,则eλ单调递减,系统状态将沿逆时针方向穿越B2区域到达滑 模 面sλ=0 上。若ėλ→0 且eλ→0,由 式(15)可知此时sλ→0,二阶系统将沿着滑模面趋近于平衡点,系统不发散。假设系统穿越B区域总时间为τ,则从相平面任意位置出发,总能在固定时间内到达滑模面并保持在滑模面上,到达时间如下

实 际 应 用 中τ→0[27]。因 此,可 以 认 为 系 统 状 态{eλ,ėλ}能够在固定时间到达滑模面。
系统状态{eλ,ėλ}收敛至滑模面后,sλ=0。如前文所述,控制器不发生奇异,对eλ求取时间导数得到

可观察到,式(30)满足文献[26]的固定时间引理,故系统状态{eλ,ėλ}能够在固定时间T2沿滑模面sλ=0 收敛到平衡点,T2满足如下表达式

故 而,二 阶 系 统{eλ,ėλ}能 够 在 固 定 时 间T1+T2收 敛 至 平 衡 点,即 由eλ构 成 的 二 阶 系 统{eλ,ėλ}固定时间镇定。
证明完毕。
综上所述,本文设计的制导律满足Lyapunov稳定性条件。在制导指令作用下,视线角误差轨迹λe严格跟踪视线角误差参考轨迹λeD,导弹能够实现打击角度和打击时间控制。
3 制导律参数寻优
导弹在视线角误差参考轨迹与制导指令的作用下,满足打击时间和打击角度的约束。由式(13)可知,只需设计制导律对视线角误差参考轨迹严格跟踪即可完成期望打击角度控制。参数δ1决定了导弹飞行轨迹,通过选取δ1构造期望的飞行轨迹,使其满足打击时间约束。故而对应不同的期望打击时间td,δ1的值也不同。设导弹真实打击时间为timp,由于导弹速度是常量,飞行距离越长、轨迹越弯曲,打击时间timp的值越大。制导律参数寻优的目标是令timp=td,此时导弹在期望的打击时间td以期望的打击角度命中目标。
定义如下性能指标

式中J表示真实打击时间与期望打击时间之间的差值。假设期望的打击时间是td,对打击时间的控制问题即转化为求解J的最小值问题。J是关于δ1的函数,通过选取δ1的值,找到J的最小值。本文使用在线优化方法对打击时间进行迭代优化,优化方法使用适合求解少变量多元方程极值的Nelder⁃Mead 算法,不需要任何求导过程即可获得合适的δ1。
文献[6,10,16]将视线角轨迹设计成含有一个未知参数的多项式,并借助优化方法对未知参数迭代寻优,从而实现打击时间的控制。本文使用的在线优化方法借鉴这一思想,通过数值循环迭代得到式(13)中δ1的最优值,从而构造满足打击时间约束的弹道轨迹。该方法具体步骤如图3 所示。
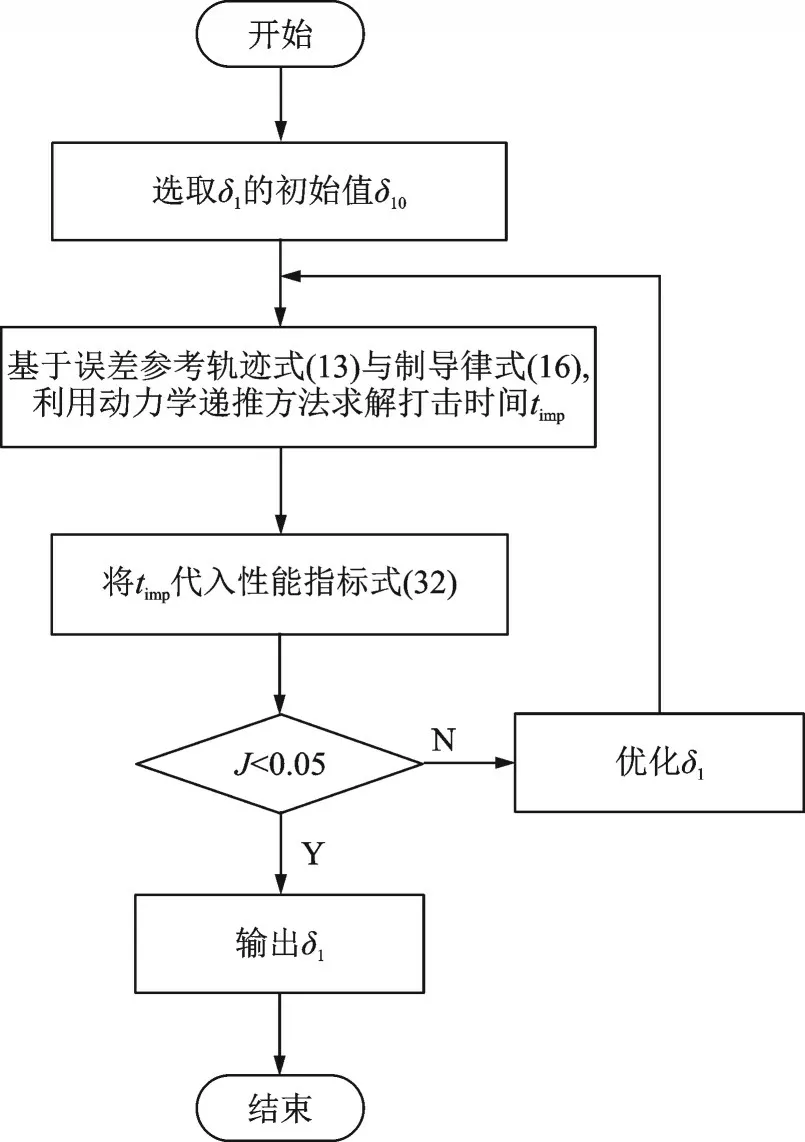
图3 在线优化计算步骤Fig.3 Computational steps for optimization routine
将使用优化方法求出的δ1表示为δ*1,并将δ*1代入式(13)得到


使用上述制导律跟踪视线角误差参考轨迹,系统状态将维持在滑模面sλ=0 上,因而确保导弹在期望打击时间以期望打击角度击中目标。本例中令δ1的初始猜测值为0.1,对应的优化指标J也存在一个初始值。经动力学递推及仿真迭代后,J满足条件J<0.05 时输出δ1,此时的δ1即为最优解δ*1。使用2.6 GHz CPU 对优化方法测试的平均时间为0.06 s,平均次数为9。虽然使用数值方法得到的δ*1相对于解析方法花费更多时间,然而本例中的优化方法运算量较小,可忽略不计。如图4 所示,仿真结果表明性能指标J收敛速度较快,最终满足优化的终止条件,得到合适的δ1。
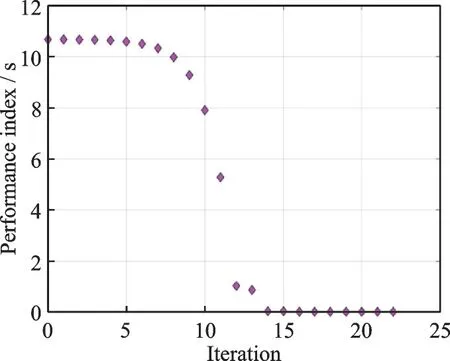
图4 性能指标收敛过程Fig.4 Convergence of performance index
所提制导算法求解过程的伪代码如下所示。仿真开始前设置制导算法的初始参数,几次寻优迭代得到最优δ1值,最终得到满足约束的非奇异终端滑模制导律。

4 仿真分析
为验证本文设计的非奇异终端滑模制导律的性能,考虑静止目标和匀速运动目标,采用式(1~4)的导弹运动学方程开展仿真验证。假设导弹的速度恒为250 m/s、初始弹道角为60°,导弹和目标的初始位置分别为(0,0)和(10,0) km。式(15,16)中的参数分别选取为p1=p2=0.7 与g1=g2=1.3。将本文设计的视线角误差参考轨迹(13)、制导律(16)以及上节介绍的优化方法在设置的初始条件下进行仿真。
4.1 针对静止目标的制导律仿真分析
首先针对静止目标开展仿真,此时目标速度为0。式(1,2)可表示为
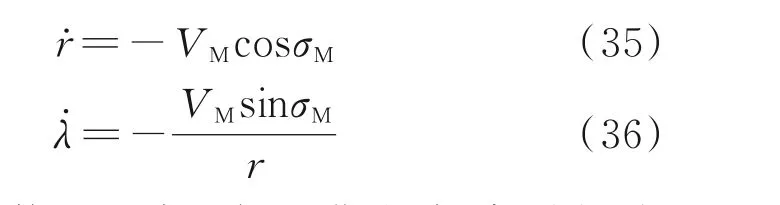
考虑一个静止目标,假设期望打击时间为50 s,期 望 打 击 角 度 分 别 为-25°,-45°和-65°。如图5 所示,仿真结果表明所提制导律对静止目标有效,系统的控制输入最终收敛至零。
考虑相同的期望打击时间、不同期望打击角度的情形。如图5(a)所示,随着期望打击角度的增大,导弹飞行轨迹进行调整以适应终端打击角度的约束。由图5(b)所示的相对距离曲线可知,导弹以期望打击时间完成零脱靶打击。导弹的视线角曲线如图5(c)所示,不同期望打击角度的视线角曲线在弹道初始阶段变化较小而弹道末段变化较大,并以各自期望打击角度击中目标。控制加速度曲线如图5(d)所示,期望打击角度越大,导弹进行轨迹调整时所需的加速度越大。3 组仿真对应的参数δ1如表1 所示。

表1 拦截静止目标的参数Table 1 Parameters for intercepting stationary targets
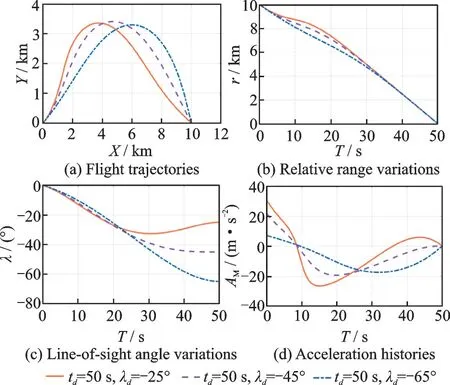
图5 不同打击角度约束下对静止目标拦截的仿真结果Fig.5 Simulation results for various impact angles against a stationary target
对表1 参数δ1在不同期望打击角度下的取值进行定性分析可知,随着期望打击角度增大,参数δ1的值随之增大。需要注意的是,针对静止目标时制导律(16)发生退化,故而制导任务开始前可对参数δ1进行离散求解,不需要在线更新参数。
4.2 针对匀速运动目标的制导律仿真分析
本小节针对匀速运动目标进行仿真验证。考虑现代舰船的典型巡航速度,将目标的运动速度设为水面舰艇的定常速度30 m/s,并假设导弹和目标的初始位置以及导弹的飞行速度与4.1 节相同。随着目标的运动,视线角误差参考轨迹进行调整,参数δ1不断迭代更新。制导框架依然不需要预测碰撞点即可满足打击角度与打击时间的约束。
将本文所提出的制导律与文献[10]所提出的制导律,在考虑不同打击角度和打击时间的情形下进行仿真对比。导弹和目标的初始航向角分别设为60°和135°,分别选取期望打击时间45 s,期望打击角度-20°以及期望打击时间48 s,期望打击角度-30°两种约束条件与文献[10]进行仿真分析,仿真结果如图6 所示。经在线寻优算法的迭代计算可知,在期望打击时间45 s,期望打击角度-20°的条件下,本文参数δ1的值为-2.281 8,文献[10]中参数a的值为-4.55;在期望打击时间48 s,期望打击角度-30°的条件下,本文参数δ1的值为-3.700 3,文献[10]中参数a的值为-2.694 7。本文和文献[10]均实现了打击角度和打击时间的同时控制。
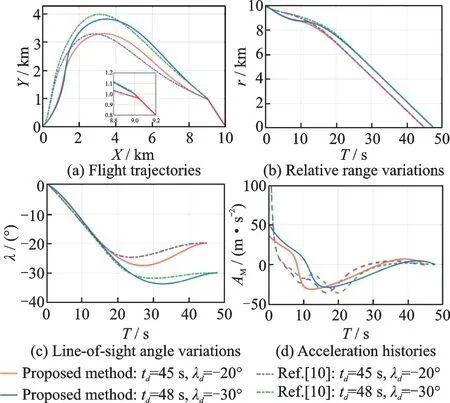
图6 不同打击角度与时间约束下对匀速运动目标拦截的仿真结果及与文献[10]的对比Fig.6 Simulation results compared with Ref.[10]for various impact angles and times against a constant⁃velocity target
由图6(a)可知,随着期望打击时间的增加,导弹飞行轨迹更长,飞行轨迹更弯曲。本文与文献[10]中目标的运动轨迹重合,在同一时刻被导弹击中,实现打击时间的控制。相比之下,文献[10]中导弹的飞行轨迹在初期上升速度更快,到达弹道顶点更早。而本文与文献[10]在弹道后半段的飞行轨迹比较接近,能够提前以期望打击角度径直拦截匀速运动目标。由图6(b)所示的相对距离曲线可知,不同的期望打击时间约束条件下,导弹分别以各期望打击时间完成零脱靶打击。在飞行时间前半段,本文的弹⁃目相对距离相较文献[10]下降速度更快;而飞行时间后半段,相对距离的变化趋势相近。导弹的视线角曲线如图6(c)所示,视线角曲线以各期望打击时间收敛至期望打击角度。本文与文献[10]的视线角变化规律在飞行时间前半段较为相近;而在飞行时间后半段,文献[10]的视线角变化更平缓,最终二者皆收敛于期望打击角度。控制加速度曲线如图6(d)所示,随着期望打击时间增加,导弹进行轨迹调整时所需的加速度增加,终端加速度最终收敛至零。假设控制输入受限为100 m/s2,文献[10]的控制加速度指令变化更剧烈,初始阶段达到限幅。弹道前半段陡增至100 m/s2,在7 s 左右下降至-20 m/s2,再缓慢变化直至收敛至0。相较之下,本文所提制导律的控制加速度指令的极值远小于文献[10],约为30 m/s2,未达到限幅。经13 s 左右缓慢降至-25 m/s2,再缓慢变化直至收敛至0。
综合来看,随着期望打击时间和期望打击角度的增加,导弹飞行的轨迹更加弯曲、终端加速度收敛到0 的速度更慢。而本文所提制导方法相较文献[10]的控制加速度具有更小的极值和变化平缓等特点,最终收敛至0 且末端无突变,更适用于工程应用。需要强调的是,所提出的制导方法考虑非机动目标。这是由于机动目标的弹道倾角在制导过程中不再是一个常数,其变化情况完全取决于目标的机动策略,此时打击角度约束无法转换为视线角约束。而本文所提出的制导方法对视线角的误差参考轨迹进行设计,不适用于打击机动目标的情形,故而针对机动目标的多项式成型方法可以通过对其他变量进行设计从而满足打击角度的约束,此处不再赘述。综合上述分析,通过对静止目标与匀速运动目标的仿真验证可知,本文所提出的制导律满足零脱靶量、打击时间、打击角度和终端加速度约束。
5 结 论
本文考虑静止目标和匀速运动目标,设计一种满足打击角度和打击时间约束的非奇异终端滑模制导律。首先考虑导弹的视线角误差,将其设计成含有一个未知参数的时间多项式以满足打击角度约束。而未知参数的引入为系统对打击时间的控制提供了可能。而后,基于固定时间稳定的概念设计一种终端滑模制导律对视线角误差参考轨迹进行跟踪,同时利用在线数值优化方法确定未知参数的值以实现打击时间控制。本文提出的制导策略不需要剩余飞行时间估计和碰撞点预测。最后,仿真结果验证了该方法的有效性。
