变质心共轴双旋翼无人机建模与反步滑模控制
2022-12-25吉思臣王司令任海鹏
吉思臣,王司令,阎 坤,任海鹏,周 洋
(1.西安工业大学电子信息工程学院,西安 710021;2.西安现代控制技术研究所,西安 710065)
共轴双旋翼飞行器是一种依靠平衡上下旋翼产生的扭矩差实现偏航控制的飞行器[1],由于其操控性强、灵活性高的特点,可在狭窄的空间进行垂直起降,无需跑道或弹射架,因此在农业、林业、多媒体、交通管制、交通运输和其他民用和军用领域得到广泛应用,特别是定点悬停和低速飞行的飞行特 性 使 其 在 执 行 高 精 度 查 询 任 务[2⁃3]时 更 具 有优势。
当前,传统共轴双旋翼飞行器依靠旋翼的周期变距来改变旋翼升力在桨盘平面上的分布情况,从而改变机身所受合力和合力矩[4],但这种控制方式存在一定的弊端。复杂的变距机构和旋转方向相反的上下旋翼造成了较快的机械磨损速度,这导致旋翼系统使用寿命低、更频繁的维护且维修成本高[5]。同时,对于只进行下层旋翼周期变距的旋翼系统,下层旋翼更容易受上层旋翼的洗流作用[6]影响,导致提供的前向推力更小,使无人机性能更差、续航时长更短。
综上,制约现有共轴双旋翼无人机进一步提高使用寿命、飞行续航和飞行性能的是旋翼系统在提供升力的同时还需要实现对机身整体的姿态控制,因此需要一种新型控制方案有效应对上述问题。
变质心控制针对这一问题提供了一种解决方案,这是依靠改变质心位置的姿态控制方法[7]。这种控制方法最早用于再入飞行器的姿态控制[8],后来在航天器、固定翼以及多旋翼的姿态控制中也得到了广泛的应用。Li 等[9]对变质心控制的发展与应用做了全面综述。变质心控制机构可完全置于飞行器内部,工作时不依赖气动力,因此它能减少机身所受空气阻力、提升续航时间。Erturk 等[10]将变质心控制应用于固定翼无人机的姿态控制,去除了机翼上的操纵舵,使姿态控制不依靠空气动力。Haus 等[11]使用变质心控制解决了燃料动力四旋翼无人机很难通过控制旋翼转速实现控制姿态,也证明了变质心控制在旋翼机上的可行性。Darvish⁃poor 等[12]使 用LQR(Linear quadratic regulator)实现了变质心共轴双旋翼在俯仰和滚转通道上控制,且完成了8 形轨迹跟踪,证明变质心控制对旋翼机具有足够高的可操作性。
本文为共轴双旋翼无人机提出了一种三轨变质心机构。变质心控制机构仅使用3 个皮带⁃滚筒结构实现姿态控制,与4 个轨道的方案[12]相比结构更简单,材料质量更轻。使用动力电池作为控制机构中的滑块,增加了无人机续航。外部采用涵道外壳设计,涵道用于抑制桨尖涡流、为旋翼系统增加升力[13],同时避免无人机受剧烈碰撞而损毁[14],提高无人机调试阶段的安全性。但变质心无人机是一种多刚体系统,其自身具有很强的非线性和不确定性,为了更直观地表示这种特性的成因,本文选用牛顿⁃欧拉法对其进行动力学建模[15],利用牛顿⁃欧拉法在物理参数计算的直观性来表示滑块运动对机体运动的影响。针对这种非线性和不确定性,本文利用反步滑模控制在非线性控制方面具有响应速度快和强鲁棒性的优势[16],完成了反步滑模姿态控制器的设计,并检验其有效性和抗干扰能力。
1 控制机构
本文所提的变质心共轴双旋翼无人机,如图1所示,在外部使用涵道用于增加能量利用效率和保护内部的旋翼系统。在涵道内部有3 个皮带⁃滚筒结构作为无人机的变质心控制机构,如图2 所示,3 个使用弹簧导线的电池分别固定在3 个皮带上,滚筒通过伺服电机驱动。变质心机构依靠皮带带动滑块运动实现质心位置改变,且3 个滑块运动的方向不在同一平面,这样保证由质心位置求出唯一的滑块位置。涵道内有两个旋翼分别存在于入口和出口附近,这两个旋翼同轴且旋转方向相反。

图1 变质心共轴双旋翼无人机Fig.1 Moving mass-actuated coaxial dual-rotor UAV
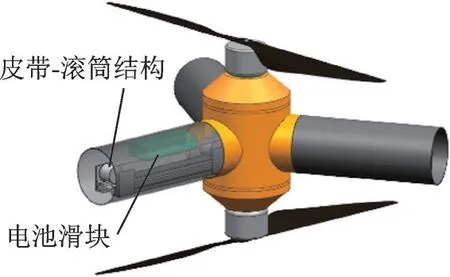
图2 三轨变质心控制机构Fig.2 Three-track moving mass control mechanism
电池滑块移动改变无人机重心的位置,导致无人机所受升力和重力的合力矩改变,以此来实现对俯仰角和滚转角的控制。旋翼系统可通过调整上层旋翼和下层旋翼的转速,改变每个桨叶所受的反应力矩,实现对偏航角的控制。
2 无人机数学模型
2.1 定义坐标系
为了描述无人机相对于地面的运动和变质心机构在无人机内的运动,引入地面坐标系Og⁃XgYgZg和机体坐标系Ob⁃XbYbZb,如图3 所示。

图3 地面坐标系与机体坐标系Fig.3 Ground coordinate system and body coordinate system
地面坐标系中,原点定义为地面上一点,Og Xg轴水平面指向正东,OgYg轴水平面指向正北,OgZg轴竖直向上,在无人机研究中,通常把地面坐标系看作惯性系。机体坐标系中,原点定义为除去变质心控制机构的无人机质心位置,坐标轴初始方向与地面坐标系平行。
2.2 运动学模型
将无人机模型简化为仅包含变质心控制机构和无人机机身2 部分的系统,变质心控制机构的质量集中在滑块上。设无人机的整个系统、变质心控制机构和无人机机身部分的质量为分别为mS、mC和mB,在地面坐标系中的质心位置矢量分别为PS、PC和PB,由质点系质心的定义得

用VS、VC和VB分 别 表 示PS、PC和PB的 对 时间的导数,根据质点系动量定理存在如下关系式
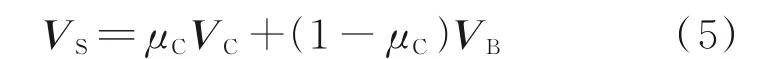
用RC表示地面坐标系下PC相对于PB的位置矢量,则三者满足如下关系
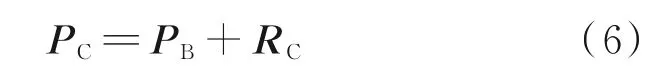
用Ω表示无人机在地面坐标系转动的角速度,则可将PC相对于PB的运动分解为平移运动和定轴转动,即
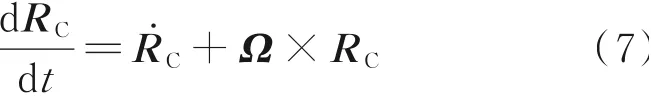
则PC相对于地面坐标系的运动速度可表示为
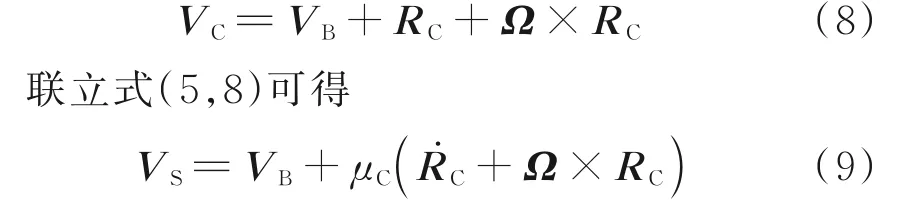
用vS、vB和vC分 别 表 示PS、PC和PB在 机 体 坐标系内的移动速度,rC=[xC,yC,zC]T表示机体坐标系下PC相对于PB的位置矢量,ω表示无人机在机体坐标系内的转动角速度,则
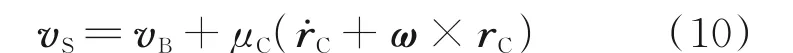
2.3 动力学模型
在机体坐标系内,变质心无人机的运动可分解为平移运动和绕质心转动。在研究变质心无人机质心运动时,可将整个无人机系统视为质点系,系统质心位置PS的运动符合质心运动定律,质点系质心的加速度只与质点系所受合外力有关。在研究变质心无人机绕质心转动时,可将整个无人机系统视为刚体,绕质心的转动符合动量矩定理,转动的角加速度只与刚体所受的合力矩有关。
2.3.1 平移运动动力学模型

2.3.2 绕质心转动动力学模型
变质心无人机绕质心转动的动力学方程同样建立在机体坐标系下。根据动量矩定理,无人机的角动量H和合力矩M=[L,M,N]T存在如下关系

式中H=J⋅ω,J为无人机整个系统绕系统质心转动的惯性矩阵。
角动量对时间的导数又可表示为
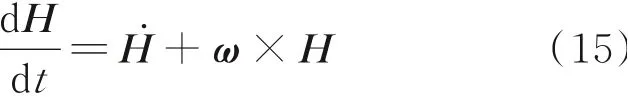
联立式(14,15)可得
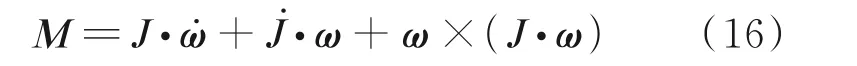
对式(16)进一步整理可得

式中E3表示三阶单位阵。
则无人机整个系统绕系统质心转动的惯性矩阵J可表示为

2.4 力和力矩
2.4.1 机身重力
在变质心无人机飞行过程中,其始终受到重力G的作用,若机体坐标系到地面坐标系的变换矩阵为Cgb[ϕ,θ,ψ],则重力在机体坐标系下可表示为

重力为过质心力,因此重力的力矩始终为0。
2.4.2 旋翼升力
考虑目前对涵道异物对流场的干扰没有准确的数学模型,因此在动力学建模时忽略滑轨外壳对流场的影响并使用控制算法对未建模部分进行补偿,利用Pitt⁃Peters 动态入流模型和叶素理论对飞行器的气动模型进行近似建模。
这里使用Pitt⁃Peters 动态入流模型[17]来求解涵道共轴双旋翼无人机的诱导速度。根据动态入流模型,共轴双旋翼产生的空气动力和诱导速度存在如下关系

式中:Mi、Vm、L分别为入流动力学的惯性矩阵、质量流量参数矩阵和静态传递矩阵;Ct、Cr、Cp分别为旋翼的升力系数、滚转力矩系数和俯仰力矩系数;λ0、λs、λc分别表示诱导入流比的时均、一阶横向分量和一阶纵向分量。在上下两层旋翼之间的存在诱导速度相互影响的情况下,诱导速度的动态变化可表示为

式中:下标i、j用于区分上下两旋翼,当i表示上旋翼时j表示下旋翼,当i表示下旋翼时j表示上旋翼;下标0 表示静止状态下无穷远处到旋翼的入流比;Kji表示旋翼j对旋翼i诱导速度的干扰系数,与设计参数有关;λfs为飞行器运动引起的入流比。
根据叶素理论[18],旋翼的升力Ti与其翼长R、弦长c、叶素桨距角δ、诱导速度λi以及旋翼转速ωi有关。记桨盘面积为A,空气密度为ρ,升力系数为Cti,旋翼升力线斜率为as和桨盘实度为σ,则作用在旋翼桨叶上的升力Ti可以表示为

式中VB,z表示机体上升的速度。
若桨叶阻力系数为Cd,旋翼提供的扭矩可表示为

2.4.3 合力与合力矩
由于只考虑变质心共轴双旋翼无人机在中、低速飞行或悬停时的情况,且使用轻质旋翼,则可忽略飞行时的涵道空气阻力和旋翼的陀螺效应。因此,无人机的质心运动主要由机身重力FG和旋翼升力Frotor的合力Fb决定,无人机绕质心的转动主要由旋翼提供的升力力矩和旋翼扭矩Qrotor的合力矩M决定。升力力矩由无人机质心到旋翼升力的着力点的位置矢量与升力矢量的矢积所决定,旋翼升力在机体坐标系Ob⁃XbYbZb内平行于ObZb,同时旋翼升力过机体坐标系原点,无人机质心到机体坐标系原点的位置矢量为-rS,则

因此,变质心无人机在俯仰和滚转通道上的姿态控制很大程度上取决于rS的数值。
3 动力学特性
对于变质心无人机的姿态控制,飞行器本身的特性、控制机构的输出量和被控量的变化特性对控制系统的设计具有重要参考意义。这里使用合力矩M、转动惯量J和角加速度ω̇的变化来反映变质心无人机的动力学特性,并分析不同的滑块位置riC和滑块总质量占比μC对无人机运动的影响。
3.1 力矩特性
无人机在进行俯仰和滚转通道的姿态调节时,引起无人机绕质心转动的合力矩为

因此,在无人机进行姿态调节时,所受合力矩M与质量占比μC、-rC在Ob⁃XbYb面上的投影以及旋翼升力Frotor有关。
3.2 转动惯量特性
以绕机体坐标系Ob Xb轴转动为例,根据式(20)可得,无人机绕Ob Xb轴转动的转动惯量可表示为
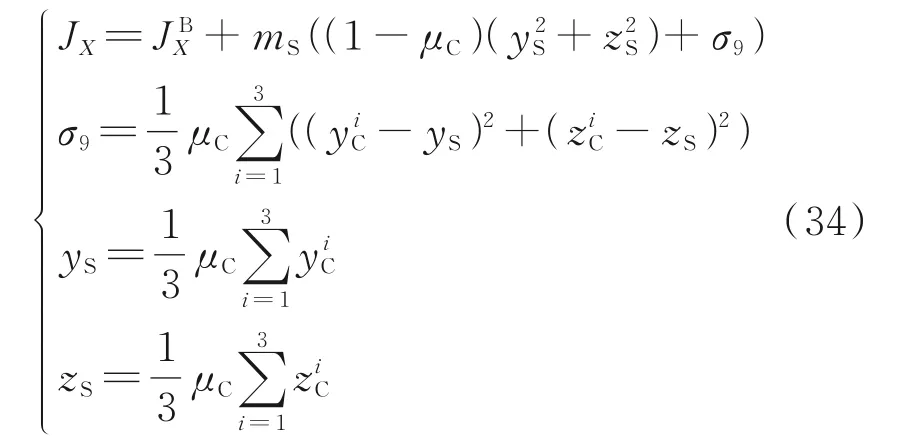
由此可推断无人机机体绕机体坐标系某一轴的转动惯量可表示为关于μC、rC的函数,因此无人机在进行姿态控制时惯性矩阵J会不断改变,如图4 所示,随着μC和yC的增大,JX逐渐加快增加速度。
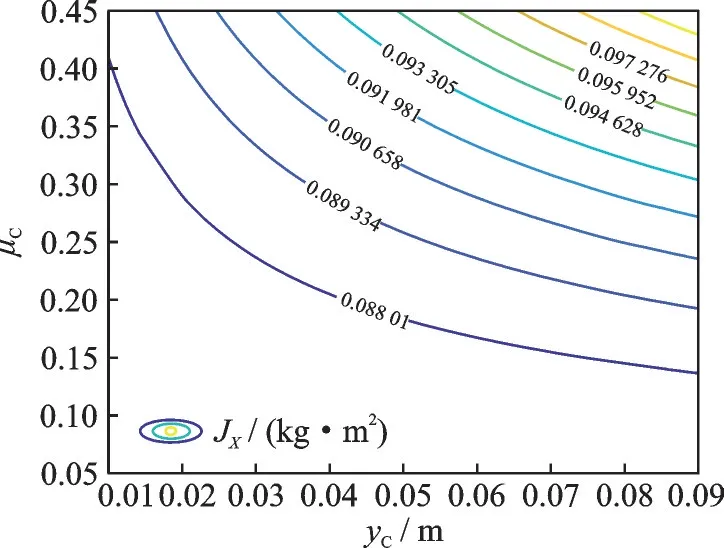
图4 转动惯量特性Fig.4 Rotational inertia characteristics
3.3 角加速度响应特性
图5 为无人机悬停状态下,不同μC和yC对应的角加速度ṗ的数值,其大小随μC和rC的增大而增大。ṗ的增加速度随着μC增大的过程逐渐加快,但随rC增大的过程逐渐放缓,因此角加速度响应特性也呈现出一定的非线性。
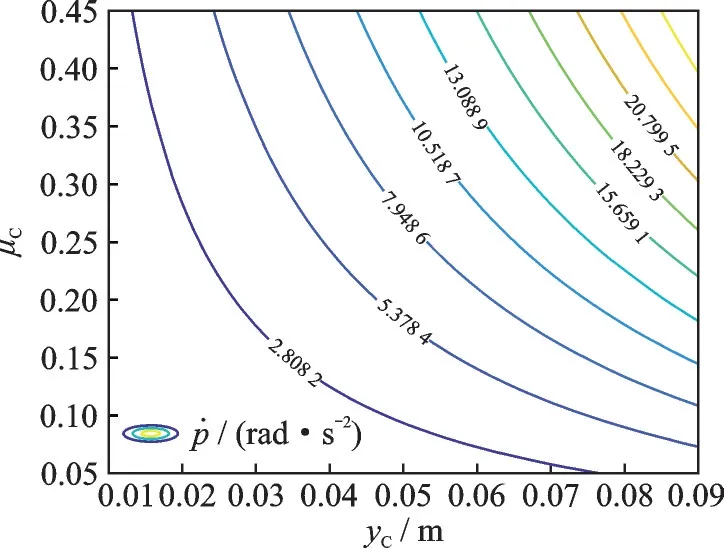
图5 角加速度响应特性Fig.5 Angular acceleration response characterristics
4 反步滑模姿态控制器
假设无人机机身的质量分布具有一定的对称性,且变质心控制机构工作时质量分布对称性改变较小,即JXY=0。则式(17)在俯仰、滚转和偏航通道上的角加速度可简化为

式中:F表示总不确定性,|F|≤Fˉ;ΔA、ΔB表示系统参数不确定部分;d(t)表示系统未建模部分和其他外部扰动。式(35)中各姿态角控制的总不确定性可表示为
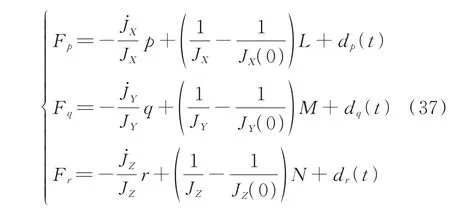
式中JX(0)、JY(0)和JZ(0)为rC=0 时JX、JY和JZ的值。则对于无人机的姿态控制系统有:Ap=0,Bp=1/JX(0),Fˉp=max|Fp|,Aq=0,Bq=1/JY(0),Fˉq=max|Fq|,Ar=0,Br=1/JZ(0),Fˉr=max|Fr|。
针对式(36)中的系统,可采用反步滑模控制[19],定 义 跟 踪 误 差z1、虚 拟 控 制 项z2、切 换 函数为ρ


式(41)中的包含描述系统特性的惯性参数B,不确定性参数Fˉ,以及与系统特性无关的参数h、c、k。只需将式(41)代入式(40)消除B和F,并使h、c、k的取值满足|P|>0,就可保证式(42)中V̇≤0。
若将姿态控制器的输出表示为期望力矩的大小,俯仰、滚转和偏航通道上的期望力矩可表示为

变质心控制机构控制滑块移动的模型较简单,可使用串级PID(Proportion integration differentia⁃tion)控制实现对r̂C的跟踪。
将式(46)中的N̂和高度控制期望的F̂rotor代入式(28),可 得 旋 翼 系 统 期 望 转 速ω̂u和ω̂l的 约 束条件
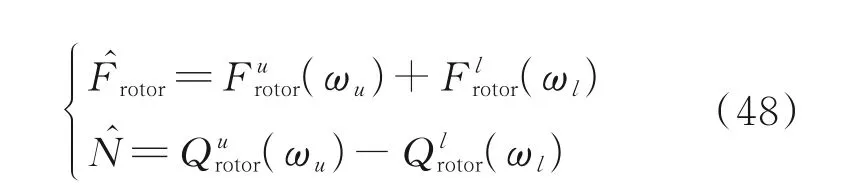
式(48)姿态控制器设计由式(35)中的简化模型推导得出,在仿真实验和实际姿态控制中JXY不可能始终为0。但得益于滑模控制具有鲁棒性的特点,可适当增加式(36)中代表总不确定性的参数F的数值,来抵抗JXY≠0 引起的各轴向控制力矩对其余轴上角加速度的干扰。
5 仿真分析
本节对上文所设计的变质心共轴双旋翼的反步滑模姿态控制器进行仿真,以验证控制器对变质心无人机这种不确定非线性系统的有效性,并进行姿态角的追踪实验;之后,对系统施加sin(2t)形式的扰动,用于模拟阵风[20],以此验证控制器的抗干扰能力;同时记录变质心控制机构质心在机体坐标系内的移动轨迹,用于检验所设计的变质心控制机构能否在不触及滑块行程最大值的情况下完成对机身姿态的控制。变质心无人机的基本参数如表1 所示,滑块行程最远0.25 m,最大滑动速度0.7 m/s。
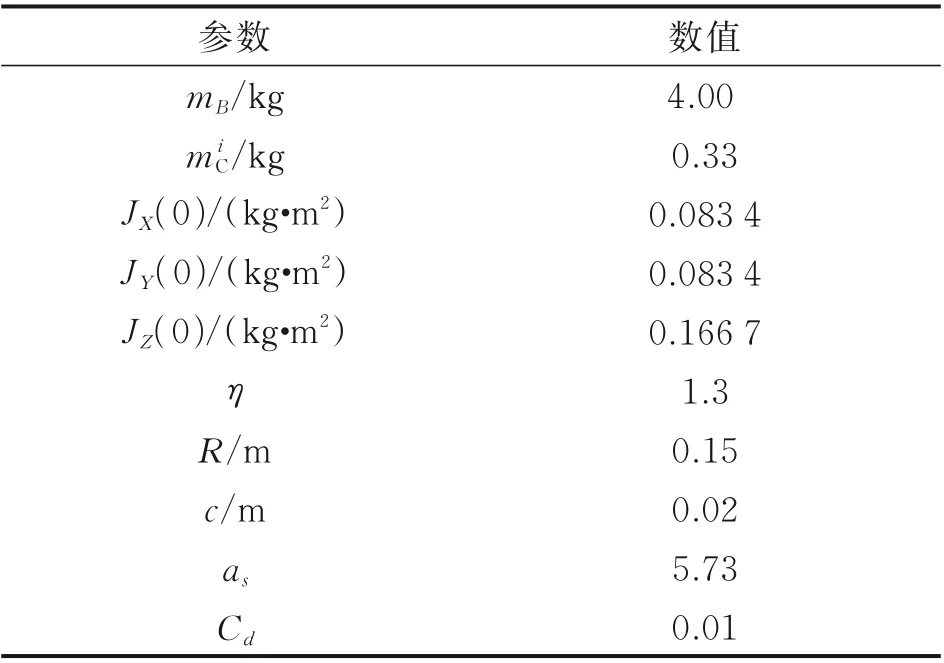
表1 变质心无人机总体参数Table 1 Overall parameters of mass⁃actuated UAV
使用tanh 函数的滑模切换项会在接近滑模面时造成控制输出抖动[19],为消除抖动也可将式(44~46)中的sgn 函数替换为tanh 函数,2 种函数的控制器在俯仰通道上的单位阶跃响应结果见图6,7。由图7 可知,tanh 函数对应的控制器输出仍具有较快的响应速度,且不会造成抖动。在后续仿真实验中控制器滑模切换项将使用tanh 函数。
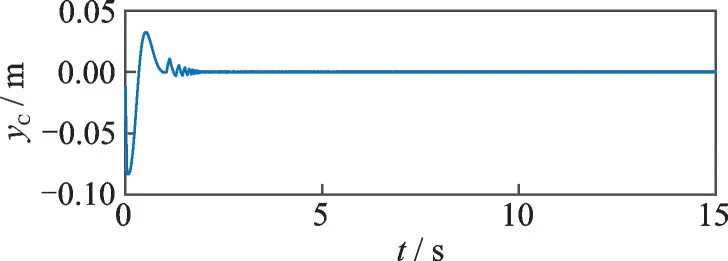
图6 sgn 切换函数对应的控制器输出Fig.6 Controller output using the sgn switch function

图7 tanh 切换函数对应的控制器输出Fig.7 Controller output using the tanh switch function
图8 考虑了式(35)中描述的角加速度变化能受其余两轴角速度的影响以及自身转动惯量变化带来的影响,给出了系统同时跟踪ϕd=0.61sin(t+π 3 ),θd=0.61sint和ψd=0.61sin(tπ 3 )的结果和误差,0.61 rad 大约是35°。由图8 可知,所设计的姿态控制器能在各轴角速度之间存在相互干扰的情况下,姿态角控制的稳态误差不超过5%。
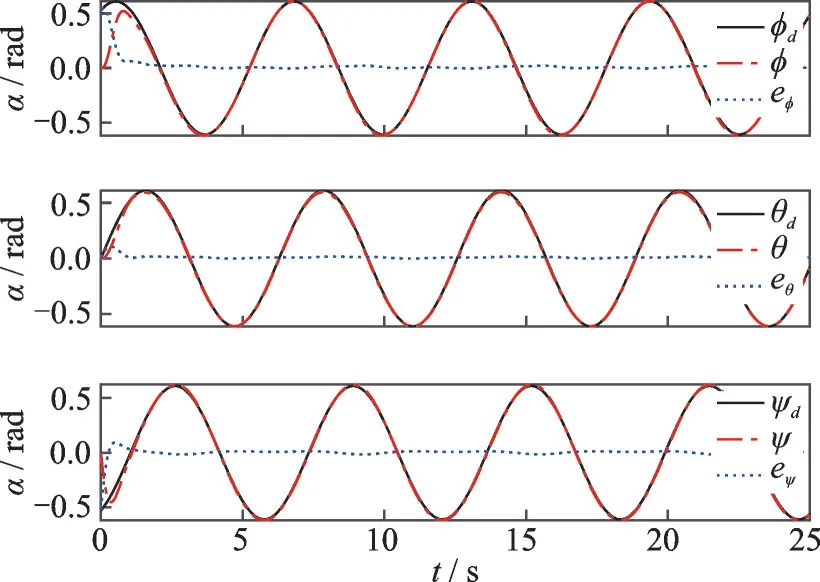
图8 姿态角跟踪的结果和误差Fig 8 Results and errors of attitude angle tracking
图9 展示了在姿态角跟踪的过程中,变质心控制机构质心位置在动态过程和稳态过程中的变化轨迹。如图9(a)所示,在动态过程中‖rC‖2的最大值0.080 6 m,而‖rC‖2所 能 达 到 的 最 大 值 为0.083 3 m,因此本文设计的变质心控制机构在幅值为35°的姿态角跟踪中未触及滑块行程边界而造成控制器性能下降。如图9(b)所示,在稳态过程中‖rC‖2的值不超过0.007 m,且rC的轨迹具有周期性,说明维持姿态角跟踪时rC的移动范围要远小于其在动态过程中的移动范围。
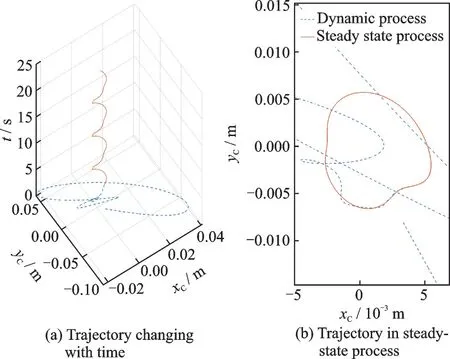
图9 变质心控制机构质心位置的变化轨迹Fig.9 Variation trajectory of the moving mass control mechanism centroid position
图10 给出了对系统施加一个sin(2t)形式的扰动时,系统跟踪的目标函数为ϕd=sint的结果和误差以及变质心控制机构质心位置随时间变化的曲线。由图10 可知,sin(2t)形式的扰动下,在动态过程中yC不超过0.06 m,未触及行程边界,动态过程不受影响。且系统稳定时的误差不超过3%,这说明此控制器具能较好地抵抗外部干扰。
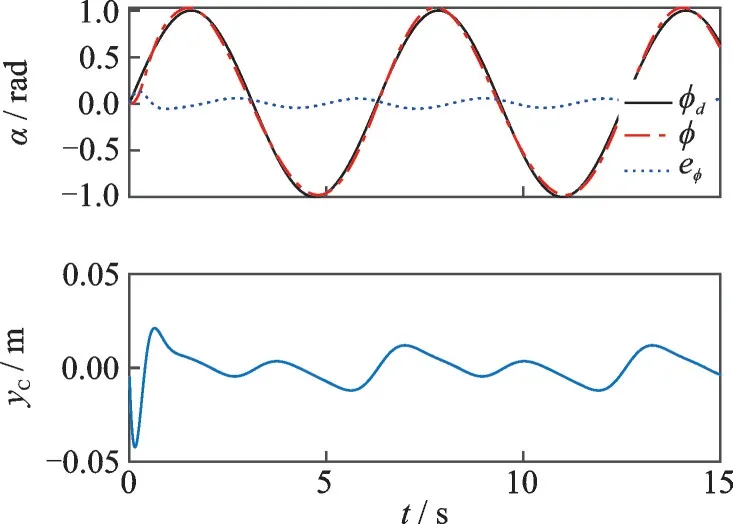
图10 受扰时跟踪结果Fig.10 Tracking results when disturbed
6 结 论
本文针对共轴双旋翼无人机的姿态控制提出一种依靠变质心机构的控制方案,仅使用3 个皮带⁃滚筒结构实现姿态控制,材料质量更轻。采用变质心控制方案使共轴双旋翼避免使用易磨损的变距机构,延长了无人机的使用寿命;同时定桨距旋翼可以提供更稳定的升力输出,便于升力控制;涵道的使用降低了旋翼系统的费效比,增加无人机的悬停时间,同时可降低旋翼系统产生的噪声。因此变质心共轴双旋翼更适用于农业、林业、多媒体等领域的低速高精度的定点查询任务。
利用牛顿⁃欧拉法推导了变质心共轴双旋翼的运动学模型和动力学模型,利用叶素动量理论建立了涵道双旋翼的气动模型,并分析了不同滑块位置和质量占比情况下变质心无人机动力学特性。建立变质心无人机姿态控制的状态方程,针对系统中的非线性和不确定性,设计了基于反步滑模控制的姿态控制器。经仿真实验表明,所设计的控制器响应速度快、稳态误差小,同时在含有外部扰动的工况下有效完成姿态跟踪任务,具备较好的抗干扰能力。
