混凝土衬砌渠道渗漏损失分析

郭超平

(山东省聊城市位山灌区管理服务中心，山东 聊城 252001)

中国是一个以农业为基础的国家，拥有庞大的灌溉渠、跨流域输水渠。农业是经济的支柱之一[1]。由于大半部分地区是干旱和半干旱地区，人们普遍认为有必要通过修建水利工程来灌溉农业作物[2-3]。山东省西部的位山灌区于1970年就建立了灌溉网络，灌区涉及聊城市的东昌府区、临清市、茌平县、高唐县、开发区的全部和东阿县、冠县、阳谷县的部分耕地，共包括89个乡(镇)，3532个行政村，控制面积5380k，耕地面积569万亩。灌区内农业以粮食种植为主，产品较单一，灌区内农作物以小麦、玉米、棉花为主，兼作花生、大豆等。该灌区每年的河水从拦河坝分流到灌溉渠的渠首，由于渗漏，大量水流经河道干渠系统的过程中流失，这也导致了盐渍化和内涝的双重威胁[4-5]。渠道渗漏的负面影响包括：淡水枯竭、地下水污染、导致内涝和盐碱化、地下水位上升导致有用土地浪费、灌溉效率降低和运营成本增加等[6-7]。渠道渗流主要取决于土壤渗透性、渠道中的水深、湿润周长、渠道几何形状、地下水位位置、流动水流速、剪切应力(移动水流在河床上的力)、渠道内水面与含水层地下水面之间的坡度、对地下水流的限制，例如排水沟[8]。河道水粘度、河道水盐度、泥沙量和大小分布、河道年龄和植物。渗透性由土壤的物理性质决定[9]。土壤分类(基于粒度)影响孔隙大小和孔隙空间百分比，以及作用于水分子的以下力，即粘附力、内聚力和重力[10]。土壤颗粒之间的空隙越大，重力损失的水量就越大。粘土和砾石的混合物起到防渗层的作用，而质地较粗糙的土壤(如沙子)具有较高的渗透率和渗透率。本文以位于山东省西部的位山灌区的7条混凝土衬砌分流渠道为研究区域，使用流入流出法进行实测渗流数据；并确定了5个经验公式在计算渠道渗流中的适用性。

1 材料与方法

1.1 研究区概况

研究区为位山灌区，该灌区位于山东省西部，地处东经115°16′～116°30′，北纬35°47′～37°03′之间。灌区涉及东昌府区、聊城经济技术开发区、聊城高新技术产业开发区、聊城江北水城旅游度假区、临清市、阳谷、在平县、冠县、东阿县、高唐县共4区1市5县，设计灌溉面积508万亩。现有输水干渠共计3条。一干渠：控制灌区东部东阿、在平、高唐3县，徒骇河以东区域，设计灌溉面积130万亩，干渠0+000～59+000段已衬砌完毕，很大程度上改善了输水输沙条件。二干渠：控制灌区中北部徒骇河、四新河以西，马颊河、小河道以东东昌府区、在平、高唐3县区部分面积，设计灌溉面积130万亩，现已对0+000～68+730段渠道已进行了衬砌。三干渠：控制灌区西部马颊河、小河道以西阳谷、东昌府区、冠县、临清4县市区全部或部分面积，控制灌溉面积达到280万亩。交通生产桥已基本满足，但调控建筑物配套程度较差。由于长期运行及资金不足，管理机构不健全，措施不力，致使工程老化退化严重，工程完好率下降。

1.2 研究方法

1.2.1渗流测量

本研究使用流入流出法进行渗流测量。使用流速仪测量流速。采用速度面积法测量流入段和所有流出段的流量。渠道宽度用电缆测量，深度用涉水杆测量。使用测量链测量伸展长度。在试验开始前24h，选择用于渗流测量的试验渠道河段的流入量保持恒定。然后，标记了到达的起点和终点。建立了一个参考点，以测量河段起点和终点的深度。河道横截面分为8～10个小节。通过涉水杆和电缆测量每个分段的水流深度和宽度。平均深度取两个连续分段深度的平均值。在使用流速仪进行流速测量之前，对流速仪进行了校准。对于小于0.6m的深度，使用单点法进行速度测量，对于0.6～2m的深度，使用两点法。

1.2.2湿周测量

在河段的4个不同位置测量河道的深度和宽度，从中计算出平均深度和宽度。使用平均深度和宽度计算湿周周长。

1.2.3土壤分类

在7个不同的位置进行了标准贯入试验，以在河道河岸下方1.5～2m的深度处获得原状样品。进行了以下试验：筛分分析、比重计分析、液限和塑限。然后根据统一土壤分类系统对土壤进行分类。结果表明，该地区的土壤类型可归类为粉壤土。粉质壤土是一种含50%或以上粉土(0.005～0.075mm)和12%～27%粘土(0.001～0.005mm)的土壤，或含50%～80%粉土和少于12%粘土的土壤。

1.2.4用流入流出发计算实测渗流

在流入流出渗流测量方法中，河段中的渗流通过水量平衡公式获得除渗流外，所有输入均已知的方程。

S=Q1-Q2-Qf-F-U-E

式中，每个变量的单位均是m3/s。S—渠道渗流；Q1—河段上游端的流入；Q2—河段下游端的流出；Qf—分流到排水渠的流量；F—排水渠的损失(本研究中为0)；E—蒸发损失，蒸发损失估计为流入流量的0.5%；U—通过减少未测量孔口的水损失(本研究中忽略)。

1.2.5经验公式

使用5种不同的经验公式，即Moritz方程、Swamee方程、Punmia方程、Kostiakov公式和Davis-Wilson混凝土衬砌渠道公式，对7条选定渠道的渗流进行了估算。

Moritz方程：

(1)

式中，S—渗透损失(单位长度)，m3；Q—流量，m3/s；V—速度，m/s；C—根据土壤类型的定值，混凝土衬砌渠道等于0.1。

Punmia公式：

K=0.349×Q0.68

(2)

式中，K—渗透损失(每平方米)，m3/s；Q—流量，m3/s；(河段开始时)

Swamee方程：

qs=KyF

(3)

式中，qs—单位长度渠道的渗流流量，m2/s；K—多孔介质的导水率，m/s；y—渠道中的水深，m；F—渠道几何形状的函数(无量纲)。

(4)

式中，b—渠道宽度，m；y—水流深度，m；m—边坡坡度(本研究中为1)。对于正常现浇混凝土衬砌，使用的渗透值为：k=1×10-7m/s。而对于开裂的混凝土衬砌，k=1×10-6m/s。

Kostiakov公式：

(5)

式中，Q—渗流量，m3/s；Qnetflow—通过渠道的净流量，m3/s；a—渠床土壤的渗透系数(流体流速和水头之间的比例系数；b：渠床土壤的渗透指数(定义土壤的粒度。公式中使用的渗透系数a和渗透指数b的值为分别为2.65和0.45。

Davis和Wilson方程：

(6)

式中，S—渗透损失(每段渠道每天)，m3；L—渠道长度，m；Pw—湿润周长，m；Hw—渠道水深，m；V—渠道流速，m/s；C—衬砌的恒定值(对于混凝土衬砌渠道，C等于1。

2 结果与讨论

2.1 实测渗流

7条选定渠道的渗透损失率如图1所示。损失率为1.4×10-7～5.1×10-7m/s，平均3.5×10-7m/s。渗透损失的变化源于渠道衬砌的状况，渠道衬砌的裂缝或块体之间的空隙促进了渗透。可以看出，7条河道中有4条超过了建议值。这是对河道维护状况不佳的间接体现。河道的照片显示，衬砌中不同位置生长着草，这表明植物根部区域存在渗漏。例如，1号河段没有杂草过度生长，是该地块中最好的，而6号河段是泄漏最严重的一个，存在大量过度生长的杂草，如图2所示。此外，维护不善的河道，其渗漏损失会急剧增加，即流入流量的45.5%。相关文献指出，维护良好的混凝土衬砌渠道的渗透损失应小于3×10-7m/s。1号河段河段和7号河段位于上游；3号河段和5号河段在河流下游，其余在中游。

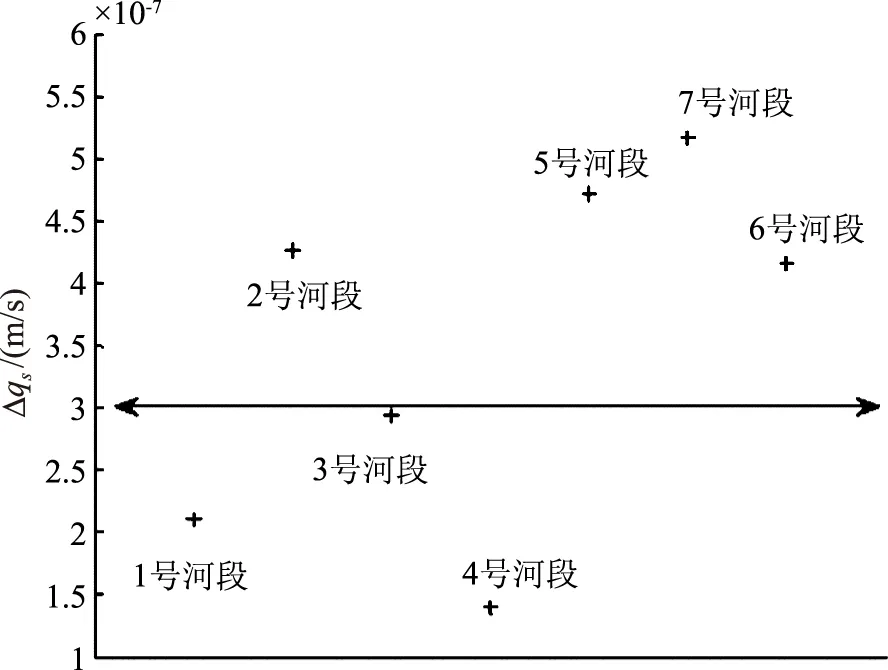
图1 比较7条渠道的实测渗透损失Δqs，其中直线表示维护良好渠道的渗透损失率上限

2.2 使用各种经验公式计算的渗流率

为了与各个方程计算结果进行比较，测量流量用试验河段的长度和湿润参数进行归一化，给出单位为m/s的渗流结果，详情结果见表1。

(1)Swamee方程

Swamee方程是作为有效最小损失渠道的设计指南推导出来的。这个渗流计算为几何变量F、水流深度和混凝土衬砌渗透性的乘积。变量F为关键变量，由混凝土的渗透性决定如图3所示。结果表明Swamee方程低估了除4号河段外的所有河道。然而，对于1号河段和3号河段，误差不超过50%。这3条渠道的实测渗透损失较小，满足了维护良好的渠道衬砌的标准。与此同时，其他4条河道的损失增加。可以合理地假设，主要不确定参数是k，即混凝土的渗透性，随着裂缝的存在而增加。这表明，通过Swamee经验公式，选择混凝土衬砌渗透性的代表值可以为渗流提供合理准确的结果。

在大多数河道中，Swamee方程低估了渗流。平均误差为-0.42，标准偏差为0.28，这是所有其他经验公式中最小的。为了改进Swamee方程的结果，建议对方程中的参数F的计算进行修改，并对比b/y进行修改，对于渠床宽度b，使用水面顶部宽度。这导致参数F的平均值增加约38%。此外，平均误差降低至-0.20，相当于平均误差减少约52%。

(2)Punmia方程

Punmia方程的性能表现的非常好，平均误差为+0.19。然而，结果中的离散程度相对较大，为0.92，与Swamee的0.28和Moritz公式的0.75相比，这是不利的。该公式以幂律形式将渗透量q与渠道承载流量联系起来，即q=cQd。系数c和d反映了实测渗流率数据库的质量。其计算结果较好的原因是，它更接近于当地衬砌条件。

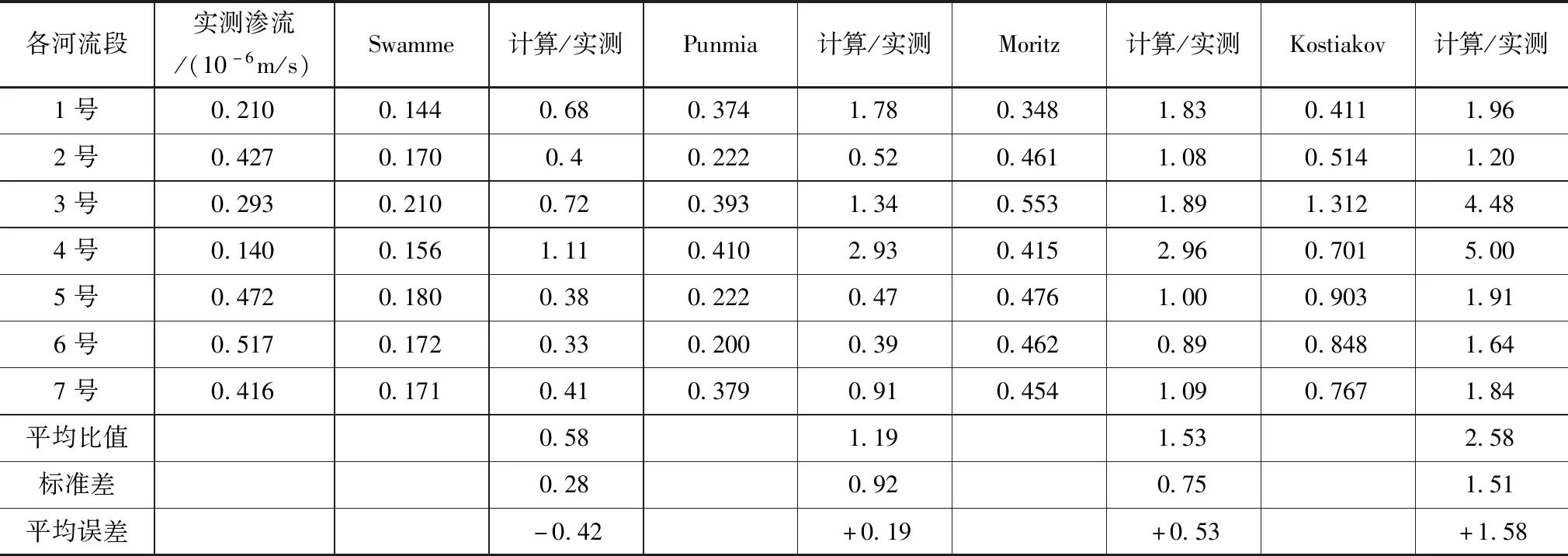
表1 使用经验公式比较实测渗流和估算渗流

图2 选取的各段河道图

图3 混凝土衬砌开裂和未开裂的渗流计算

(3)Moritz方程

(4)Kostiakov公式

Kostakov公式以q=cQd幂形式表示渗流，其中c和d分别取决于渗透系数和渗透指数，Q表示渠道河段的净体积流量。参数c和仅以土壤质地表示，并从中给出的表格中选择。由于对土壤质地的描述很少，故使用考虑稳定渗流状态的土壤特性。Kostiakov公式与Punmia方程具有类似的幂律形式。然而，Punmia方程仅在Kostiakov公式取决于土壤渗透性的情况下，才是流量体积率Q的函数。此外，流量体积率Q也是Kostiakov公式性能相对较差的原因，也可能是由于长期试验达到现场未达到稳态渗流条件。

(5)Davis-Wilson方程

Davis-Wilson方程结果计算的渗流量体积很小(约10-6)。与测量结果相比，因此未显示。其性能不佳的原因可能与以下事实有关：渗流随着水深的增加而变化，达到1/3的幂次方。另一个原因可能是，它不适合当地的条件。

3 结语

本研究使用流入流出法对研究区7条衬砌渠道进行了渗流测试。与其他方法相比，该方法对流量测量误差更小。利用现场渗流数据，利用5个经验渗流公式，即Davis-Wilson、Kostiakov、Moritz、Punmia和Swamee，对渗流估算进行了比较研究。观测证据表明，衬砌完整且裂缝较少的渠道泄漏较少，而从衬砌裂缝中生长较多杂草的渠道泄漏较多。实测公式和经验公式结果存在差异的原因主要是流量测量的不确定性、混凝土衬砌中是否存在裂缝以及经验公式中出现的参数值的不确定性。本研究的可以帮助渠道设计工程师使用经验公式准确估计渠道的渗流，有助于参与河道系统规划、设计和运营。