冲击载荷下锚杆托板及组合构件力学性能试验研究
2022-12-24吴拥政周鹏赫付玉凯孙卓越
吴拥政,周鹏赫,付玉凯,孙卓越
(1.煤炭科学研究总院 开采研究分院,北京 100013;2.中煤科工开采研究院有限公司,北京 100013;3.天地科技股份有限公司 开采设计事业部,北京 100013;4.煤炭资源高效开采与洁净利用国家重点实验室,北京 100013)
0 引 言
冲击地压是煤矿地下工程中的一种动力灾害,90%以上冲击地压事故发生在巷道中[1-3]。随着开采深度和强度增加,巷道冲击危害性愈加严重,与普通巷道相比,冲击地压巷道不仅受静载作用,还受到冲击载荷的影响[4-5]。锚杆支护是煤矿巷道最常用的支护方式,已经研发出高强度、高延伸率、高冲击韧性锚杆(索)及NPR锚杆/索等支护材料[6-9]。锚杆托板及W型钢护板是锚杆支护系统中的关键构件,在支护系统中起到扩散预应力、增大锚杆的工作阻力、改变围岩状态,抑制顶板离层等重要作用。在受到冲击载荷作用时,支护构件与围岩间作用力瞬间增加,导致托板弯曲、撕裂或围岩破碎等[10-12]。
专家学者对锚杆托板力学性质研究主要集中在以下2方面:①在托板力学性能研究方面,杨更社等[13]研究托板与围岩相互作用关系,得到托板受力表达式,分析了托板对锚杆杆体内力分布的影响;刘双跃等[14]用弹性理论分析普通蝶形锚杆托板的内力分布状态,提出托板失稳判据,研究了各参数对托板强度的影响;郑仰发等[15]通过实验室加载试验研究了不同板厚、不同拱高的可调心蝶形托板承载力与变形特征,并根据拱形托板承载力理论关系推导得到孔口极限承载力关系式,得到托板承载力与钢板厚度、拱高与拱底圆直径之比呈正增长关系;刘少伟[16]利用试验机对托板进行压缩试验,并基于弹性力学的旋转球壳理论计算分析,得到调心托板在受到偏心载荷作用下孔口处部位材料的屈服破坏准则,提出了偏心载荷作用在托板球壳上的水平分力是使托板失效的主要原因;任建峰等[17]采用尼龙PA66、高强度平垫、尼龙PA6、镀锌垫片和弹垫等减摩垫片进行了低转矩和高转矩2种状况下预紧力矩同预紧力转化效率试验;孙大增[18]基于理论分析推导托板各部分受力变形公式,利用数值模拟软件得到不同载荷条件下变形量,结合数字散斑研究方法得到托板力学行为特征。②针对托板结构变形特性,王开松等[19]采用实验室加载试验验证有限元ANSYS数值模拟分析,Q345材质厚8 mm的托板可满足煤矿深部开采支护需求;康红普等[20]、吴建星等[21]制作测力托板,用于静载条件下托板与试验台不同接触方式应力分布特征研究;何杰等[22]利用落锤冲击试验机,对托板进行低能量冲击、循环冲击试验,得到托板厚度、拱高和面积是影响其抗冲击性的关键因素;林健等[23]利用锚杆支护应力场试验台,与金属托板进行比对分析,揭示了木垫板对锚杆预应力的影响规律;笔者等[24]对托板在内的锚杆构件力学性能进行了系统阐述,并开展了缓冲垫层组合结构冲击试验研究。
从现有的研究成果来看,锚杆托板的研究主要集中在力学性能和结构变形特征两方面,研究条件主要集中在托板的静载荷,冲击载荷下托板的动态力学性能及托板+W型钢护板组合构件的力学性能研究较少。另外,针对托板动载力学特性研究采用正向冲击研究手段,与实际支护受力方向相反,无法判断正向冲击与实际受力方式的力学特征是否具有一致性。鉴于尚无托板正、反向冲击试验及组合构件的动载研究,笔者采用实验室试验方法,利用落锤冲击试验机对锚杆托板及组合构件进行动载力学性能测试,获取托板的冲击力时程曲线、位移时程曲线及变形特征等,分析托板及组合构件的力学响应规律,为冲击地压巷道锚杆托板的选择提供参考。
1 托板静载力学特性分析
托板静载试验选取煤矿常用的拱形托板,尺寸为:150 mm×150 mm,厚度10 mm,拱高32 mm,材质为Q235。将托板平放在JAW-1500微机控制电液伺服试验机,通过力控制的方式进行加载,加载速率为1 000 N/s。依据MT146.2-2011《树脂锚杆 第2部分:金属杆体及其附件》要求,静载试验时,当托板拱高变形量达到原高度30%停止加载试验,为了确保试验结果的可靠性,选取的托板重复3次试验,托板加载前后变形形态如图1所示,托板静载压力曲线如图2所示。
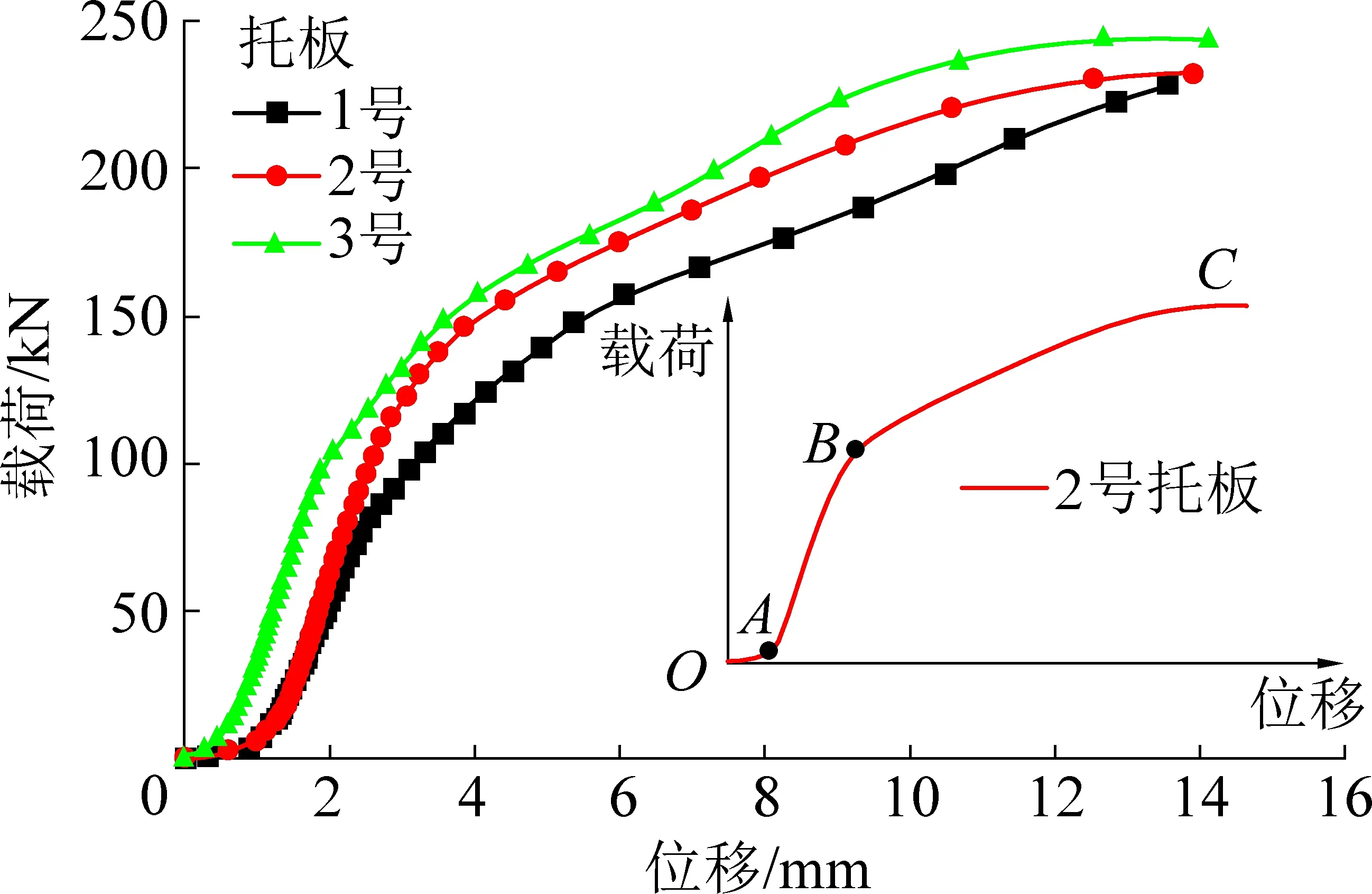
图2 托板静载压力Fig.2 Static load-displacement of supporting plate
从图1可以看出,托板拱部与底部的连接部位为承载力作用的重要位置,连接部位呈圆环形,托板变形与此位置相关。具体表现为:托板在缓慢的加载初期,四角与试验台作用,承载力逐渐增大,同时拱高逐步降低,此时连接部位未发生变化;随着载荷的增加,托板连接部位将逐渐向圆心转移,底部四角逐步翘起,拱高持续降低,达到试样承载力。
由图2可以看出,3个托板的承载力分为228、232、243 kN,最大变形量分别为13.56、13.87、14.10 mm。托板载荷-位移曲线变化趋势一致,以2号托板为例进行分析,曲线呈现“S”型,可分为3个阶段。非线性变形阶段(OA):承载力缓慢增加,曲线呈现“凹”型,托板孔口开始产生微小变形,底部与试验台开始相互贴合;线弹性应变至微塑性产生阶段(AB):曲线接近直线,卸载后可以完全恢复原本形态;塑性变形阶段(BC):B点作为托板承载力弹塑性转折点,进入本阶段托板拱高将会发生明显降低,同时托板的四角轻微翘起,连接部位逐渐向圆心转移。
2 落锤冲击试验
2.1 试验系统
冲击试验采用自主研发的落锤冲击试验机系统,由托板基座、DIT204Z落锤冲击试验机及数据采集系统等组成。落锤冲击试验机高度8 m,有效冲击高度5 000 mm,有效冲击能量最大为50 000 J,本次冲击试验的锤体质量453.5 kg,最大冲击速度7.67 m/s。试验过程中,系统配备高精度传感器,通过多通道高速采集系统,可自动采集记录落锤锤头冲击力时程曲线、应变时程曲线等,自动分析冲击参数,采样频率2 MHz,动态载荷测量误差<2%。多通道高速采集系统自身带宽为500 kHz,确保冲击力值传感器和位移传感器的信号值域准确性。托板反冲基座为500 mm×500 mm×500 mm立方体,配有托板限位装置,锤头M24的材料为合金工具钢,淬火后硬度为58~62 HRC,其尺寸大于锚杆托板尺寸,可研究试样中托板的变形特性,为拱形托板形态的改进及后续试验研究做充分准备工作。冲击试验装置如图3所示。
2.2 托板试样冲击方案
冲击载荷试验与静载试验选取的托板为同一厂家生产批次,材料属性、托板尺寸、结构特征基本相同。在煤矿井下锚杆支护巷道中,锚杆托板底部与巷道围岩直接相互作用,冲击能量作用下,托板底部受力瞬间发生形变,冲击力传递到托板拱部,即反向冲击(图4b);正向冲击情况下(图4a),试样整体稳定性好,但与实际受力来源方向相反。为研究冲击作用方向及W型钢护板对托板力学性能是否存在影响,设置了托板反向和组合构件冲击试验进行对比研究,试验采取托板正向(符号G)、反向(符号F)和托板+W型钢护板组合构件(符号GH)3种冲击形式进行,托板冲击结构如图4所示。

图3 落锤冲击试验装置Fig.3 Drop hammer impact test equipment

图4 冲击试验示意Fig.4 Schematic of impact test
试验主要研究3种试样在冲击形式下动载冲击力学性能,每种工况重复3次试验。试验时,将托板放置落锤冲击试验台的托板基座上,调整试样与落锤锤体中心处于一条垂线;调整落锤所需能量的高度,锤头做自由落体运动(g=9.806 65 m/s2)冲击试样,冲击能量为mgh(m为锤头和锤体总质量,h为下落高度);冲击过程利用锤头自身携带的传感器以及锤体上的高精度位移激光测距仪,可获得冲击力时程曲线、位移时程曲线以及试样的弹塑性形变。
3 托板冲击力学响应特征分析
3种试样冲击试验结果一致性较好。落锤冲击试样时,由于刚度较高的锤头和试样直接冲击接触,落锤锤头将会发生几次弹跳,但弹跳高度远小于冲击高度,试样处于弹性变形范围内,可忽略不计。
3.1 托板正向冲击力学响应特征规律分析
3.1.1 正向冲击破坏形态
利用落锤冲击试验机对托板开展逐级能量增加单次冲击试验,试样共10组,施加的冲击能量从500 J到5 000 J,每次增加500 J。托板冲击后变形形态如图5a所示。
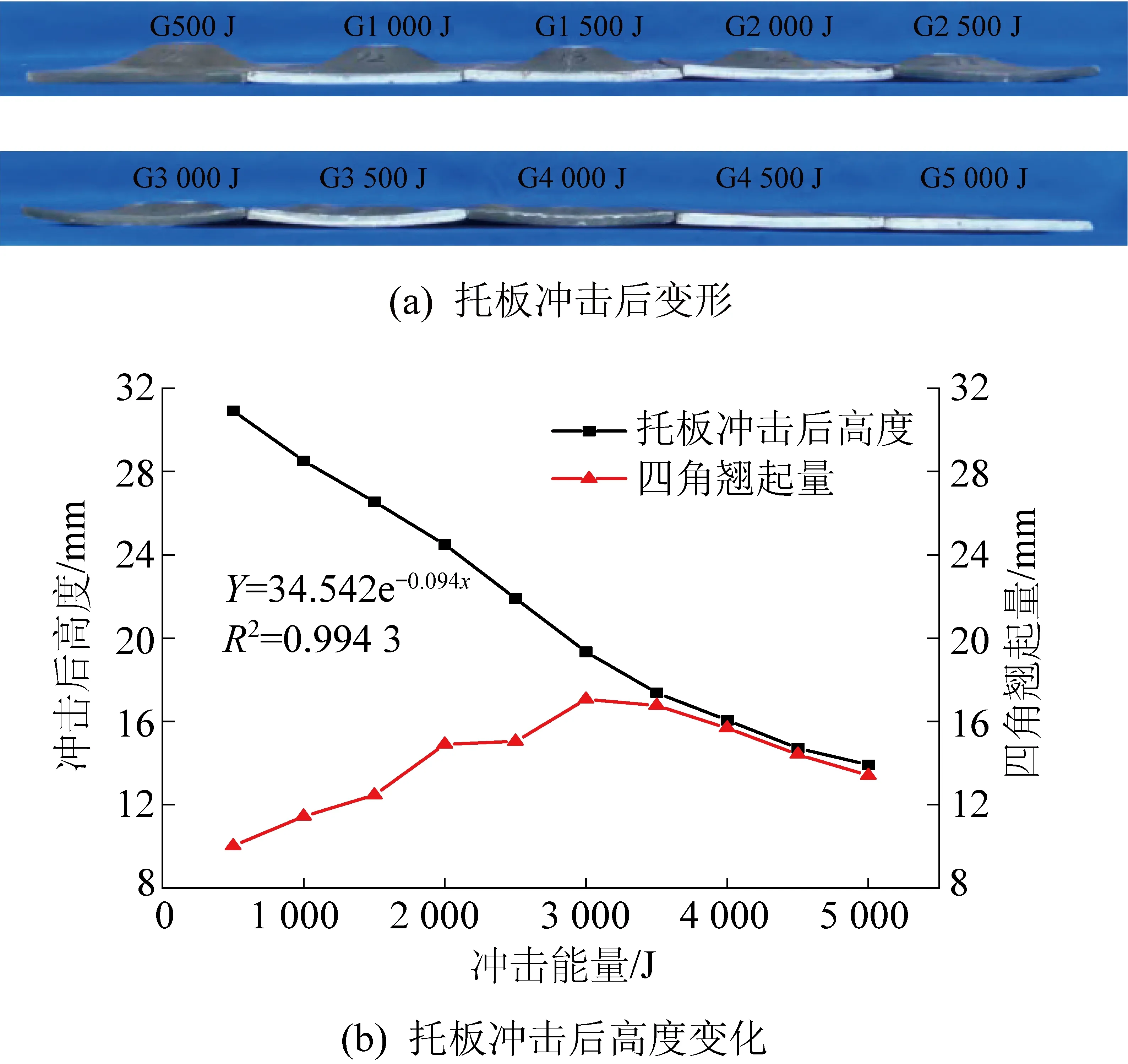
图5 托板冲击后变形形态Fig.5 Deformation shape of supporting plate before and after impact loading
四角翘起量等于托板厚度与四角翘起高度之和,从图5b可以看出,托板变形可分为以下3个阶段:托板拱高逐渐降低,四角翘起量逐渐升高(冲击能量500~3 000 J)、拱高等于四角翘起量(3 000~3 500 J)、拱高与四角翘起量同步降低(3 500~5 000 J)。冲击能量在500~3 000 J,托板拱高从30.92降至19.34 mm,降低量达39.71%,四角翘起量从10.02增至17.06 mm,翘起量增高7.06 mm;3 000~3 500 J区间托板拱高与四角翘起量基本相等;3 500~5 000 J区间,托板拱高从17.38降至13.92 mm,降低量达56.37%,四角翘起量从16.76降至13.40 mm,翘起量降低3.36 mm;整个冲击过程,随冲击能量增加托板拱高呈现指数递减趋势,高度趋近于托板厚度,即托板拱部完全坍塌。
3.1.2 托板时程曲线分析
托板正向冲击力和位移时程曲线如图6所示。
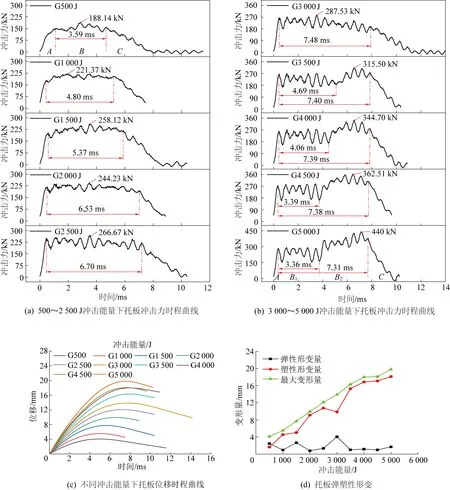
图6 托板正向冲击时程曲线Fig.6 Impact mechanical response curve of supporting plate
1)根据冲击力时程曲线是否发生二次震荡可将冲击能量划分为2个等级,即低能量冲击(500~3 000 J)和高能量冲击(3 500~5 000 J)。低能量冲击力时程曲线(以500 J为例)可分为急剧上升阶段A、震荡作用阶段B和迅速下降阶段C,冲击能量小于2 000 J,震荡作用阶段表现为震荡稳载,大于2 000 J,表现为震荡下降;高能量冲击力时程曲线(以5 000 J为例)与低能量冲击曲线存在较大差异,除急剧上升阶段A和迅速下降阶段C,震荡作用阶段分为震荡稳载阶段B1和震荡上升阶段B2。从图6a、图6b中可发现,在冲击力作用时间内,冲击力峰值全部位于震荡作用阶段,随着冲击能量增加,低能量冲击震荡幅度明显小于高能冲击。
2)随着冲击能量的增加,托板冲击力时程曲线呈现2个特征。一是托板冲击力的峰值:①低能量冲击阶段,托板冲击峰值从188.14 kN增至287.53 kN,增幅达52.83%,与托板的拱高变化呈现近似线性关系;按静载托板承载力峰值相等的要求,托板试样可抵抗2 000 J冲击能量破坏。②高能量冲击阶段,托板冲击力峰值持续增大,从315.50 kN增至440 kN,增幅达39.46%,时程曲线会出现二次震荡上升现象,与拱高和四角的形变相关,如冲击能量持续增加,冲击力峰值只与锤头和托板的刚度相关。二是冲击力作用时间:①急速上升阶段,冲击能量为500 J时,冲击力作用时间为1.01 ms,其他冲击能量力作用时间均小于0.50 ms。②随着冲击能量的增加,震荡作用时间逐渐增加,从3.59 ms增至7.48 ms,作用力时间增加了108.36%,高能量冲击是低能量冲击作用时间的2倍;高能量冲击作用时间基本相等,但震荡稳载阶段作用时间从4.69 ms降至3.36 ms。
3)根据曲线形变量特征,位移时程曲线可分为弹塑性变形和回弹变形两阶段。如图6c所示,弹塑性变形阶段变形量与作用时间呈现线性关系,随作用力时间的增加,托板的拱高变形量将会趋于某一固定值,即托板拱高与厚度之差,其中回弹变形阶段时长平均占作用时间34.28%,平均形变量为1.71 mm。如图6d所示,在低能量冲击时,回弹变形形变量在0.79~2.66 mm,在高能量与低能量冲击转折点,回弹形变量可达到4.05 mm,此现象的发生与拱高和四角翘起量之间的高度相关,即协调变形存在差异,拱高与四角翘起高度相等,共同抵抗冲击变形。在冲击力作用下,最大变形量为试样弹塑性形变之和,结束时变形量为试样塑性变形量。按托板拱高变形量要求,试样可抵抗2 500 J冲击能量破坏。
3.2 反向冲击对托板力学响应规律分析
为研究冲击作用方向对托板力学性能是否存在影响,设置了托板反向冲击试验进行研究,与正向冲击的变形、冲击力及位移时程曲线进行对比分析。
3.2.1 反向冲击变形特征
根据正向冲击托板破坏特征,选取冲击能量1 000、2 000、3 000、4 000、5 000 J,进行5组能量单次反向冲击试验,正-反向托板冲击变形如图7所示。
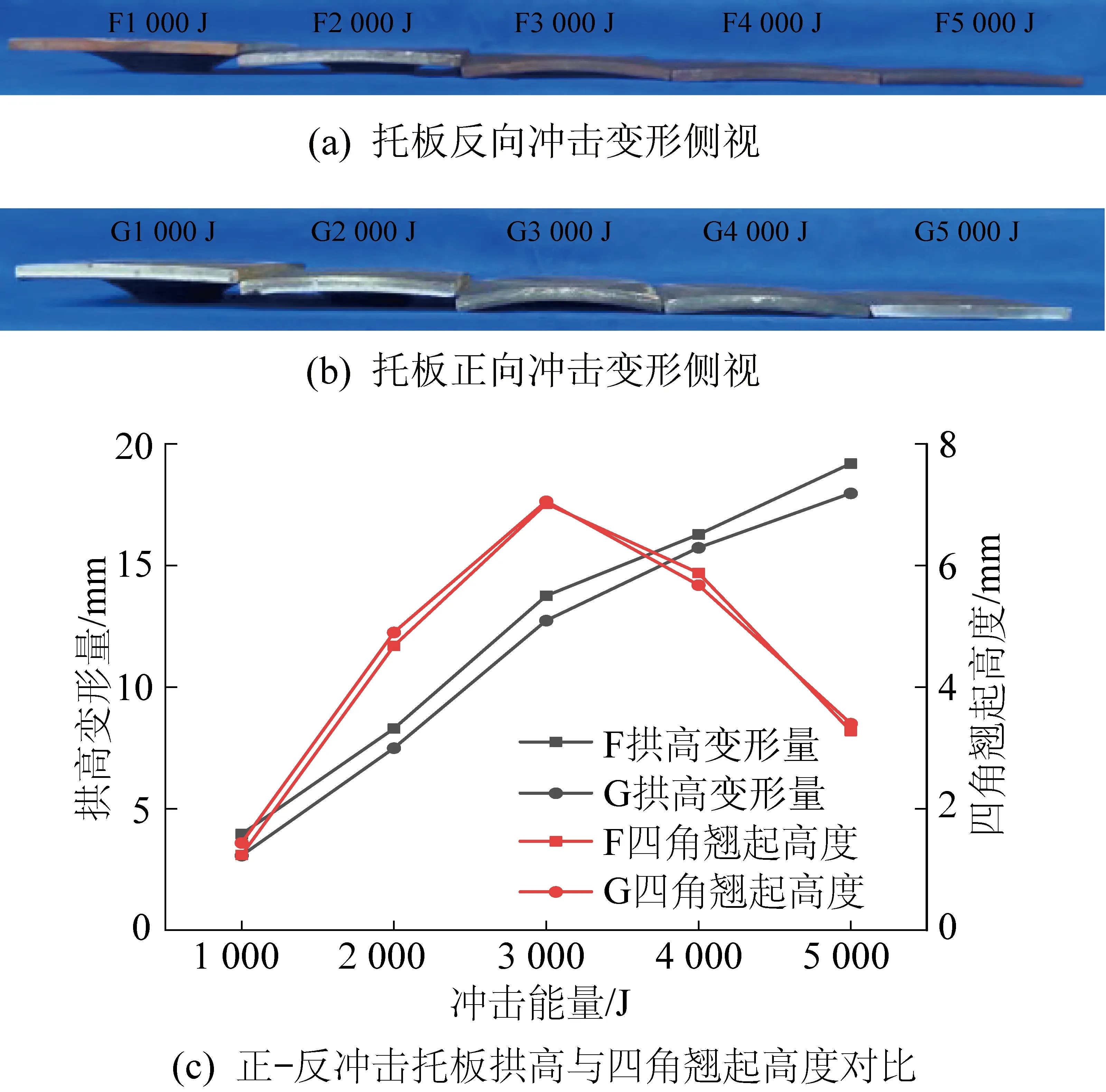
图7 托板正-反冲击变形形态Fig.7 Deformation shape of supporting plate after positive-negative impact loading
从图7可知,试样正向冲击与反向冲击试验相对比,在拱高和四角翘起高度的变化趋势具有一致性。在5种冲击能量下,反向冲击拱高变形量分别为3.96、8.30、13.76、16.28、19.20 mm,拱高分别降低12.45%、25.82%、42.63%、50.62%、59.96%,正向冲击拱高变形量分别为3.08、7.50、12.74、15.74、17.98 mm,拱高分别降低9.75%、23.44%、39.71%、49.50%、56.36%,反向冲击试样拱高变形量略大于正向冲击,变形量最大相差3.6%。低能量冲击,反向冲击与正向冲击试样四角翘起高度分别为1.24、4.68、7.02 mm和1.44、4.90、7.06 mm,正向冲击翘起高度大于反向冲击;高能量冲击,反向冲击与正向冲击试样翘起高度分别为5.88、3.28 mm和5.68、3.40 mm;整个冲击两试样四角翘起高度相差最大值为0.22 mm,变化趋势在冲击能量为3 000 J由增加转变为降低,相差高度仅为0.04 mm。总体来看,试样正向冲击与反向冲击四角翘起高度一致性较好,反向冲击试样拱高形变量略大于正向冲击,整体形变规律趋势相同,试样冲击变形形态具有较好的一致性。
3.2.2 正-反冲击时程曲线
为进一步评价试样正向冲击与反向冲击是否存在差异,结合试样冲击力时程曲线、位移时程曲线以及吸能特性,进行对比分析,由图8可以看出:
1)反向冲击力时程曲线可分为3个阶段,冲击力急速上升阶段、震荡作用阶段、迅速下降阶段。随着冲击能量的升高,同正向冲击可划分为2个能量级,冲击力时程曲线变化与正向冲击轨迹形态一致性较好,反向最大冲击力为246.91、272.59、284.22、333.28、415.29 kN,正向最大冲击力为221.37、244.23、287.53、344.70、440 kN,正、反向冲击的最大冲击力全部位于震荡作用阶段,冲击力峰值最大相差28.33 kN;在相同冲击能量条件下,反向与正向冲击震荡作用时间分别为4.79、6.15、7.49、7.38、7.34 ms和4.80、6.53、7.48、7.39、7.31 ms,震荡作用时间最大相差仅0.38 ms。反向冲击的冲击力时程曲线与正向冲击存在微小差异,即每个阶段曲线具有微小震荡波动,原因为锤头与托板底部优先接触,托板孔口处与试验台接触,在受到冲击作用时,托板稳定性较差造成震动的产生;此外,由于震荡导致反向冲击上升阶段作用时间大于正向冲击阶段,最大时间差达0.62 ms。总体来看,根据冲击力时程曲线分析,正向冲击与反向冲击规律相同,结果具有一致性。因此,可认为2种不同冲击方向的托板试验冲击力变化规律基本相同。
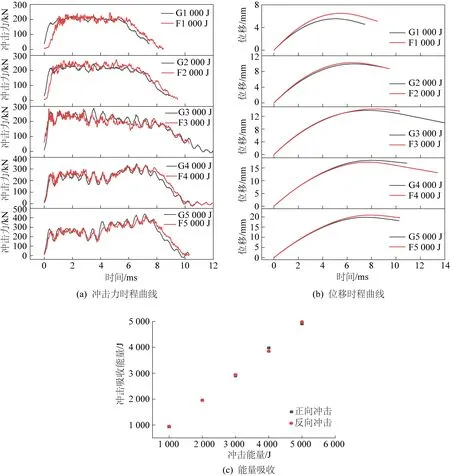
图8 正-反冲击曲线对比分析Fig.8 Comparative analysis of positive-negative shock curves
2)反向冲击位移时程曲线分为2个阶段:弹塑性变形阶段和回弹变形阶段。弹塑性变形阶段,随着冲击能量升高,反向冲击托板最大变形量为6.50、10.30、14.30、17.30、20.90 mm,正向冲击最大变形量为5.50、9.90、13.90、18.00、19.80 mm,最大差值为1.10 mm;反向与正向冲击最大变形量作用时间分别占整个冲击过程64.94%、67.62%、79.90%、57.68%、76.11%和67.65%、74.18%、54.60%、73.37%、73.49%,整个过程中,反向与正向冲击最大变形量平均作用时间占比分别为69.25%和68.66%;回弹变形阶段,反向与正向冲击弹性形变量分别为1.40、1.62、0.65、4.18、1.33 mm和0.95、0.79、4.05、1.15、1.68 mm,平均形变量为1.84和1.72 mm,最大差值为3.40 mm,反向冲击回弹变形在冲击能量4 000 J时达最大值,相比正向冲击3 000 J,存在滞后现象,其余冲击能量最大相差仅为0.83 mm;反向与正向冲击作用时间分别为2.97、3.07、2.07、5.68、2.48 ms和2.41、2.29、6.41、2.90、2.72 ms,两者平均作用时间为3.25和3.35 ms,在协调变形区间差值占比可达30.74%和25.53%,与托板四角翘起高度、拱高共同抵抗冲击变形相关。托板反向与正向全过程平均作用时间分别为10.41和10.32 ms,由位移时程曲线最大变形量、回弹形变量及分别作用时间对比,托板正、反向冲击结果在协调变形转化区间存在一定差异,其他冲击能量水平下力学规律一致性较好。
3)综合1)和2),从能量角度研究发现(图10c),随着冲击能量的升高,能量转化率逐渐升高,反向冲击吸收能分别为947.70、1 958.38、2 940.86、3 849.16、4 984.92 J,平均转化率为97.33%;正向冲击吸收能分别为928.38、1 956.93、2 897.44、3 977.70、4 907.52 J,平均转化率为96.97%;在反向冲击能量为4 000 J时、正向冲击能量为3 000 J时,由于托板拱高与四角翘起量协调变形存在较小差异,造成转化率低于正常值。在相同冲击能量条件下,能量转化率相差仅3.21%,差值仍处于试样协调变形转换区间。对比发现,托板正、反冲击转化率基本相同,可认为2种冲击形式下力学响应规律相同。
综合上述,试样整个冲击过程中在协调变形转换区间,由于托板四角翘起高度与拱部变形不协调,造成弹塑性变形存在部分差异,但不影响托板整体力学规律。反向冲击稳定性较差,为了增加试样的稳定性,建议托板采取正向冲击开展试验研究。
3.3 组合构件冲击力学响应特征分析
在锚杆支护系统中,锚杆托板与W型钢护板组合护表构件是常见的护表方式之一。为此,开展了锚杆托板+W钢护板冲击力学特征试验研究,托板试样选取与前述试验属同一批次。利用落锤冲击试验机对10组组合试样进行了单次冲击,冲击能量与3.1节相同。
3.3.1 组合构件变形特征分析
组合构件冲击后的变形形态如图9所示。由图9a和图5a可知,组合构件中托板与单独托板冲击变形规律一致性较好。随着冲击能量的增加,组合构件中托板拱高变形量从1.16增至18.34 mm,冲击能量为5 000 J时,变形率达57.31%,单独托板冲击拱高变形率达59.96%。在托板承载范围内,组合构件中托板四角翘起高度整体小于单独托板冲击作用。由此可见,组合构件可以减缓托板结构变形。
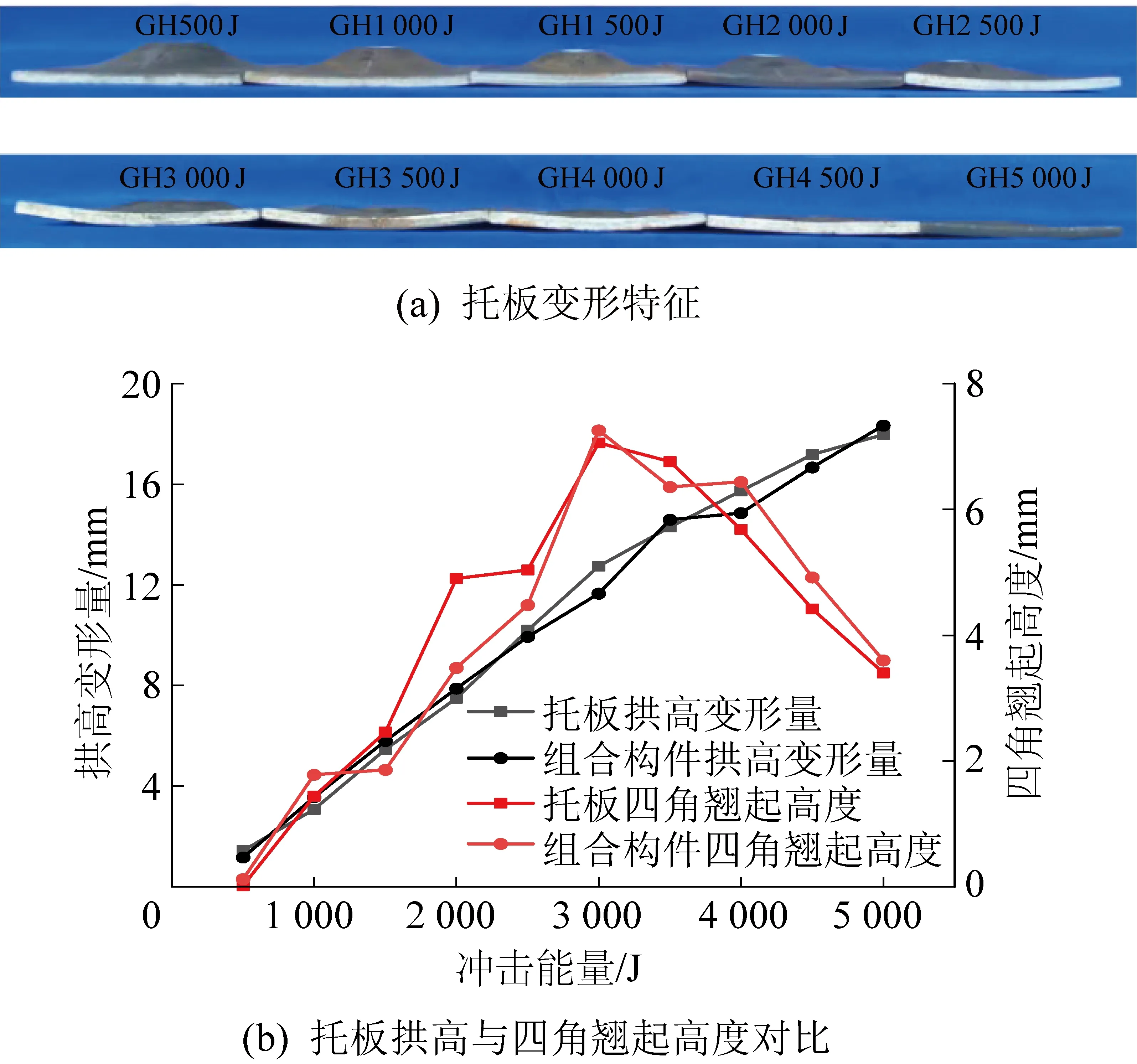
图9 组合构件中托板及单独托板冲击变形形态Fig.9 Deformation form of combination components of supporting plate and supporting plate
3.3.2 组合构件时程曲线
根据时程力学曲线变化形式,选取低能量2 500 J、试样协调变形转换区间3 500 J、高能量4 500 J等3个能量级别冲击力时程曲线和位移时程曲线进行对比分析。
从图10可以看出:
1)图10a为试样的冲击力时程曲线。从曲线可以看出,与单独托板相比较,组合构件的冲击力时程曲线出现明显差别,冲击力作用时间均大于12.00 ms,平均比单独托板冲击作用时间长3.50 ms。组合构件冲击力时程曲线(以4 500 J为例)分为:初期震荡阶段D、急剧上升阶段A、震荡作用阶段B、迅速下降阶段C和尾部震荡卸载阶段E5个阶段。3种能量条件下,初期震荡时间分别为1.58、1.62、1.38 ms,尾部震荡卸载阶段时间分别为0.42、2.25、4.37 ms,与单独托板冲击震荡作用阶段时间6.70、7.40、7.38 ms对比,组合构件作用时间为6.17、7.37、6.82 ms,平均震荡作用时间偏小0.37 ms;组合构件和单独托板冲击力峰值分别为256.69、291.01、458.26 kN 和266.67、315.50、362.51 kN,低能量冲击时,组合构件小于单独托板冲击力峰值。整体来看,在低能量冲击时,可见组合构件通过缩短震荡作用时间和降低冲击力峰值提高托板抗冲击性能;在高能量冲击时,组合构件主要通过缩短震荡作用时间提高托板抗冲击性能。
2)图10b为试样位移时程曲线。从曲线可以看出,位移时程曲线分为弹塑性变形和回弹变形两个阶段。弹塑性变形阶段,组合构件与单独托板最大变形量分别为17.23、22.40、23.60 mm和12.08、16.34、18.09 mm,作用时间分为别8.80、9.83、8.62 ms和7.21、7.95、7.59 ms,与单独托板对比,组合构件最大变形量平均增加5.57 mm,作用时间平均延长1.50 ms,平均作用时间占比为66.66%;回弹变形阶段,组合构件与单独托板弹性形变量分别为1.04、2.32、6.33 mm和1.32、1.05、0.99 mm,作用时间分为别2.66、4.55、6.42 ms和3.18、2.41、2.03 ms,与单独托板对比,组合构件回弹变形量平均为3.23 mm,偏大2.11 mm,作用时间平均延长2.00 ms;对比分析发现,组合构件可以增加弹塑性变形阶段的最大变形量和回弹变形阶段的回弹形变量,延长分别作用时间,降低最大变形量作用时间占比,来提高组合构件整体的抗冲击力学性能。
组合构件10组冲击试验中,单独托板与组合构件反弹速度、吸收能量测试结果见表1。
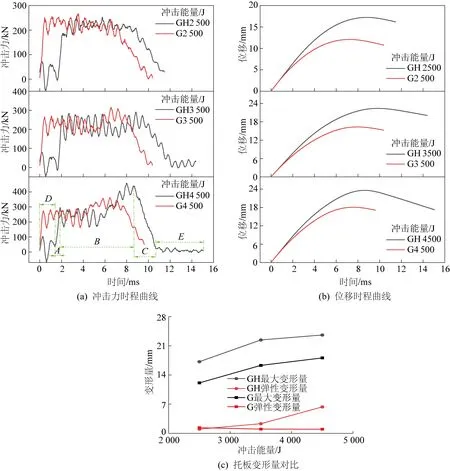
图10 组合构件时程曲线Fig.10 Impact mechanical response curve of mechanical response curves of combination components
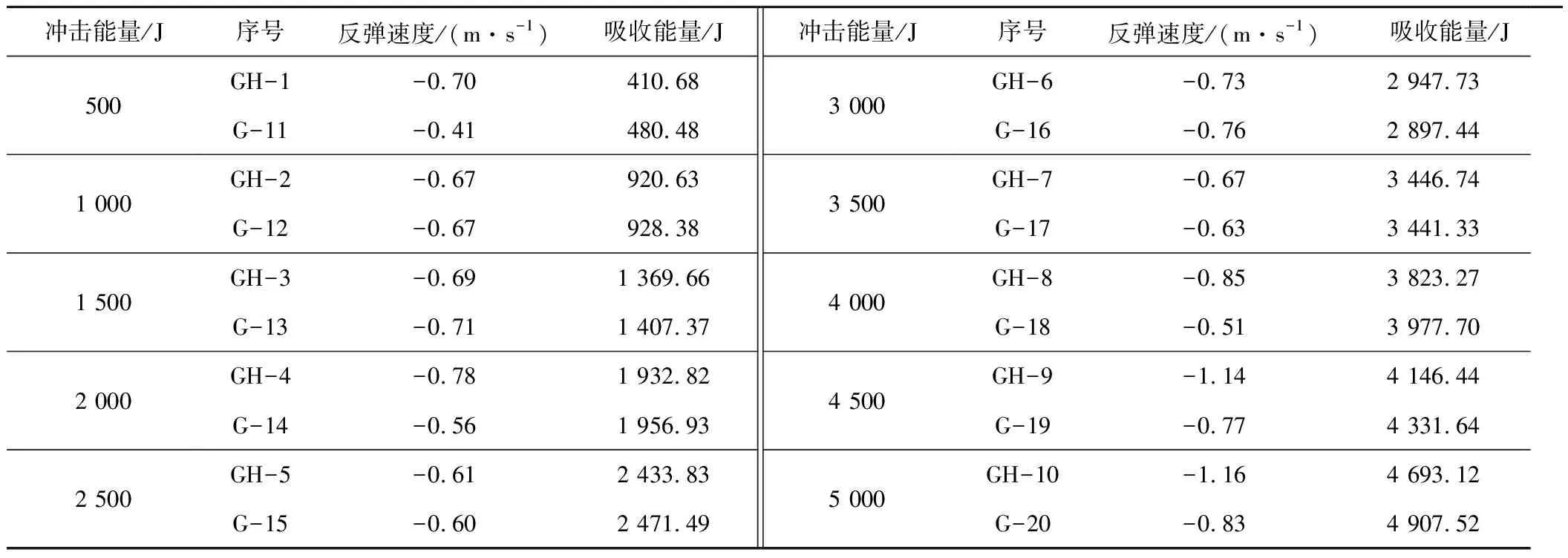
表1 组合构件与单独托板测试方案及结果
由表1可知:根据物体质量与速度之间的关系,反弹速度与冲击能量吸收紧密相关。计算可得,随着冲击能量的升高,组合构件与单独托板能量转化率逐渐增加,后者转化率明显大于前者,组合构件平均转化率为93.78%,单独托板可达96.82%。整体来看,组合构件能量转化率低于单独托板,组合构件具有一定吸收能作用。
4 结 论
1)静载作用下,托板变形表现为拱高降低、四角翘起、连接部位向圆心转移;动载作用下,托板变形均经历拱高降低、四角翘起及压平3个阶段。托板正、反向冲击试验一致性较好,组合构件可以减缓托板结构变形。
2)托板冲击力时程曲线呈现急速上升、震荡和迅速下降3个阶段。随着冲击能量的增加,试样的冲击力峰值均逐渐增大,与静载相比,托板试样的动载荷峰值较大。与托板相比,组合构件时程曲线增加初期震荡和尾部震荡卸载阶段,具有吸能、改善托板力学特性。
3)托板位移时程曲线可分为弹塑性变形阶段和回弹变形阶段,组合构件可降低弹塑性变形阶段作用时间占比,提高托板抗冲击力学性能。
