高压XLPE 电缆主绝缘典型缺陷形态对电场畸变影响的仿真分析
2022-12-23夏俊峰施楠楠孙建生
夏俊峰,施楠楠,孙建生
(上海电缆研究所有限公司 特种电缆技术国家重点试验室,上海 200093)
0 引言
随着我国电网容量的扩大改造以及城市化进展的加快,超高压电缆的应用日益增多。电压等级的提高对电缆绝缘品质提出了更高的要求。目前超高压电缆主绝缘主要采用交联聚乙烯(XLPE)。主绝缘中存在的微孔、杂质及界面突起等缺陷易造成局部电场集中,是导致电缆故障的重要原因[1]。
主绝缘缺陷的几何形态对缺陷处的电场分布有重要影响[2]。目前,现行的高压电缆国家标准有GB/T 11017.1—2014[3]、GB/T 18890.1—2015[4]和GB/T 22078.1—2008[5],以上标准分别对110,220,500 kV 电缆绝缘中,以及半导电屏蔽与绝缘界面上的微孔、杂质及突起的最大允许尺寸进行了相应规定。文献[6]基于针板电极系统研究了绝缘内杂质尺寸对电树枝生长的作用,企业在电缆制造中也强调了对半导电屏蔽与绝缘界面的光滑程度的控制[7],但这些研究均未涉及缺陷形态对电场分布的影响。
本工作从模拟超高压电缆主绝缘存在的典型缺陷的形态出发,对电缆绝缘内部微孔、半导电屏蔽层进入绝缘层内部的突起和绝缘进入半导电屏蔽层内部的突起等3 种典型缺陷分别建立几何模型,通过有限元法计算缺陷处的电场分布,研究了缺陷形态对电场畸变的影响。
1 模型建立
1.1 几何模型
XLPE 电缆绝缘中产生电场畸变的缺陷主要有绝缘内部的微孔及绝缘-半导电屏蔽界面突起。相较于电缆绝缘,这些缺陷的几何尺寸均很小,一般在数微米至数十微米量级,其形态可近似为椭球形[8]。在二维建模中,微孔类缺陷可近似为椭圆,界面突起类缺陷可以近似为圆弧,包含缺陷的电缆主绝缘几何模型见图1。
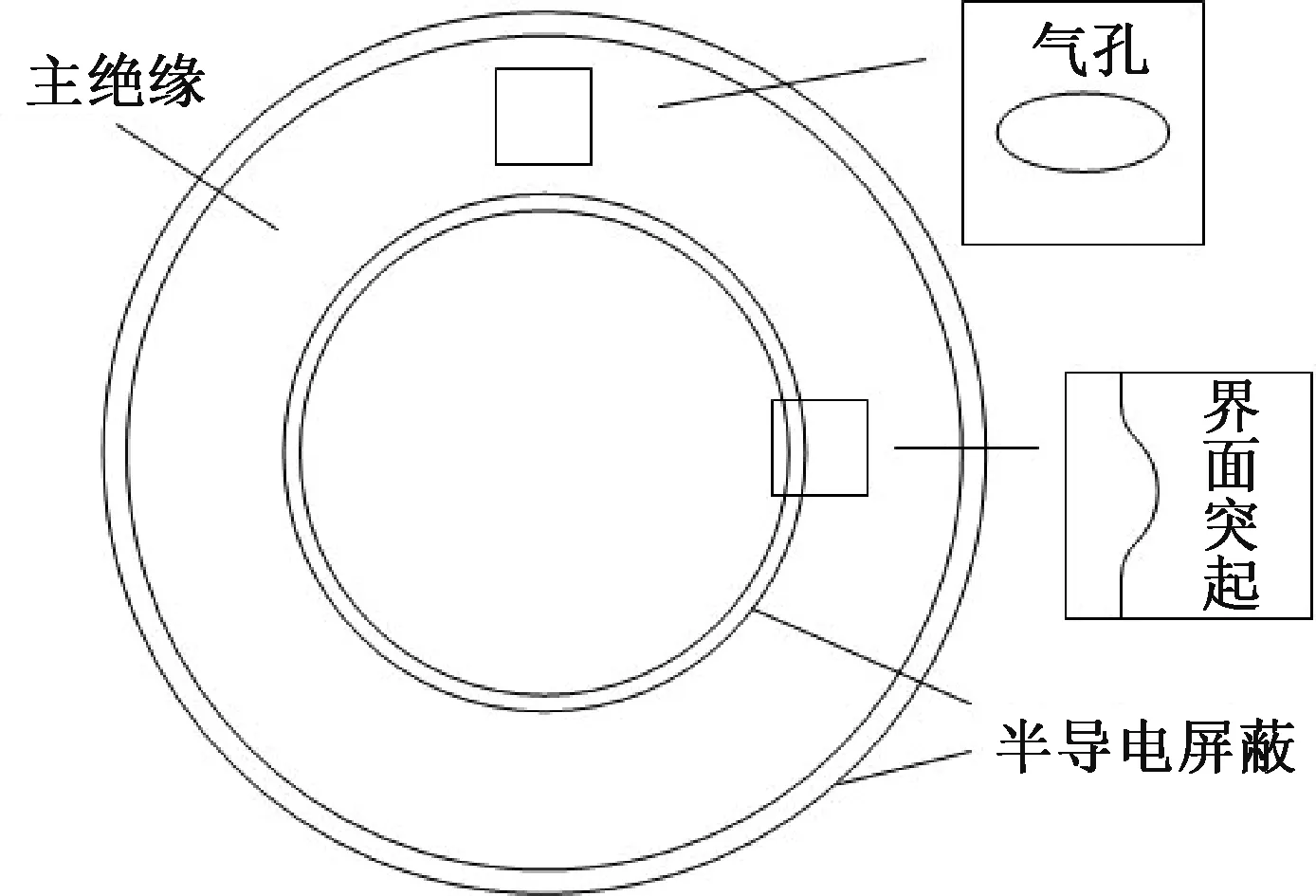
图1 包含缺陷的电缆主绝缘几何模型
假定缺陷处电场方向沿x轴正方向,对于微孔类缺陷,其形态可以通过3 个参数表示,即微孔长轴长度a,短轴长度b,以及长轴与电场方向的夹角(取向角)θ,其中a和b的取值决定了微孔的大小,a和b的比例决定了微孔的形状,θ决定了微孔的取向,其几何建模见图2。
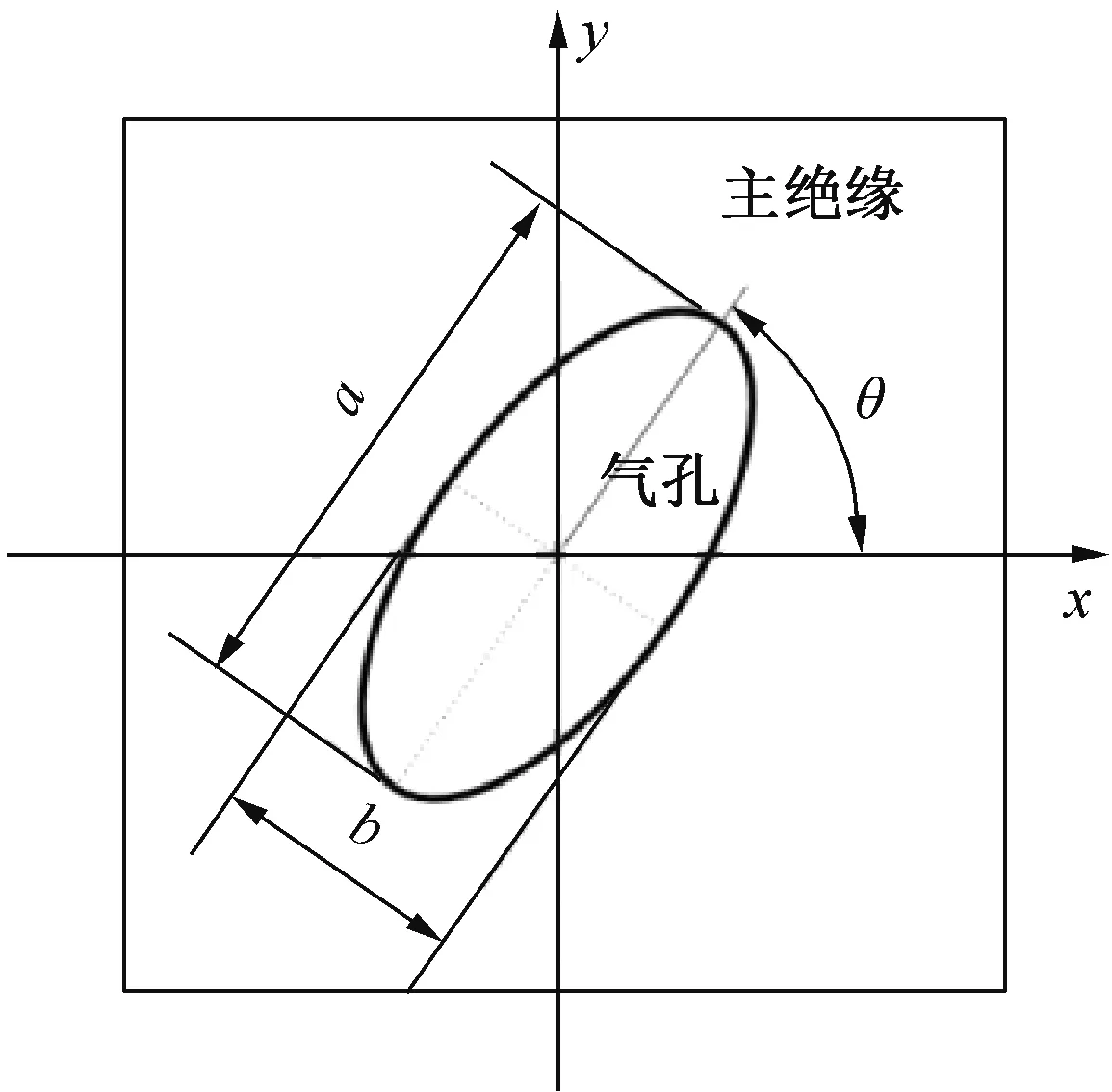
图2 绝缘内部微孔形态的几何建模
对于界面突起类缺陷,其形态也可以通过3 个参数表示,即界面突起高度H,界面宽度L,突起界面与基底平面交界处的曲率半径R,参数的取值决定了突起的大小,参数之间的比例决定了界面突起的形状。半导电屏蔽进入绝缘突起的几何建模见图3,绝缘进入半导电屏蔽突起的几何建模见图4。通过改变形态参数的大小并计算相应的电场分布,可以模拟突起类缺陷的形态对缺陷处电场畸变的影响。
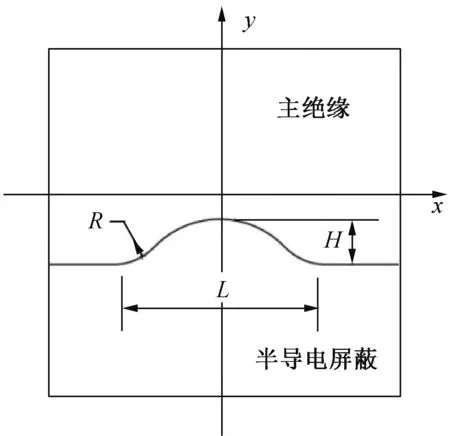
图3 半导电屏蔽进入绝缘突起形态的几何建模
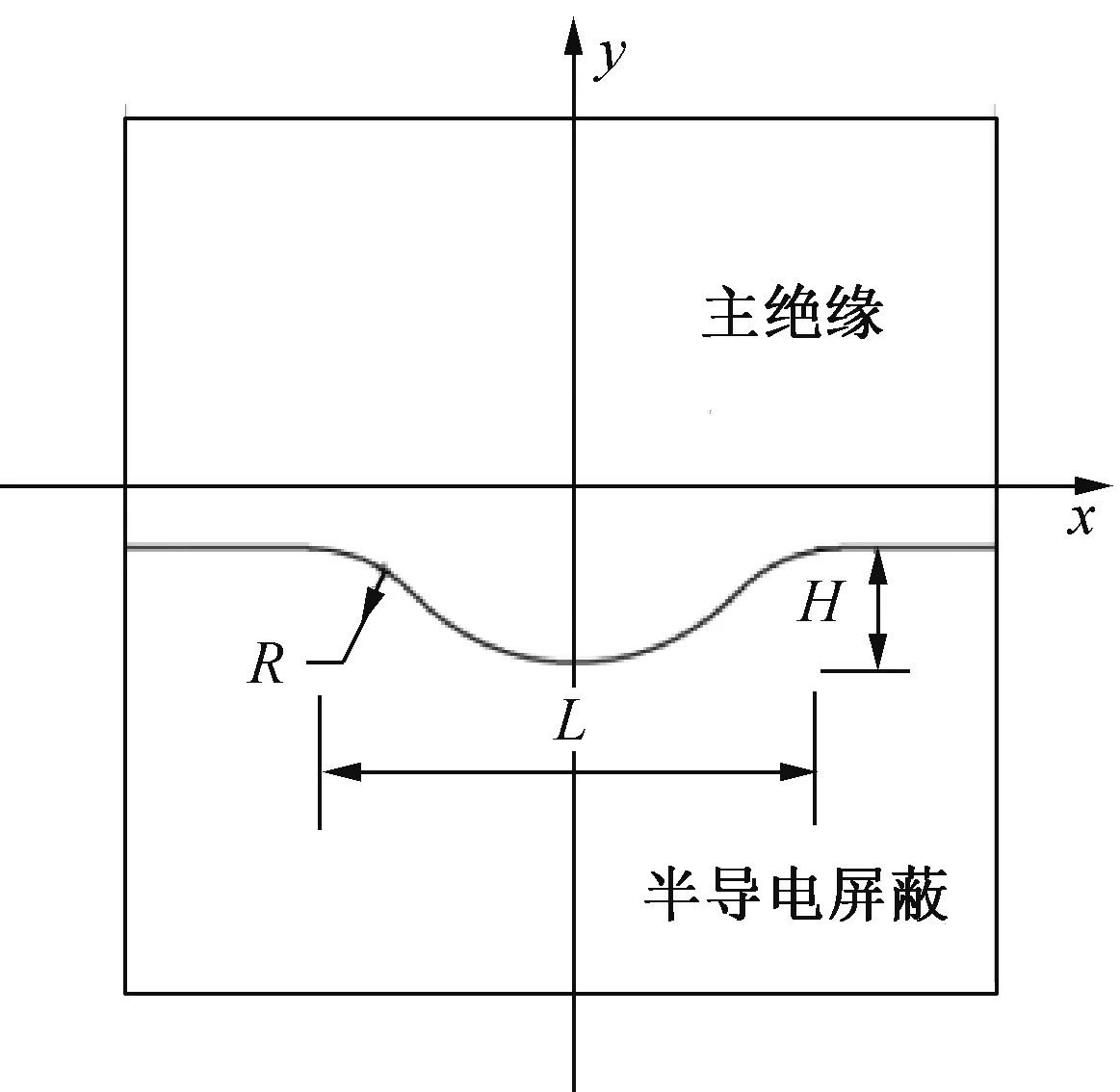
图4 绝缘进入半导电屏蔽突起形态的几何建模
1.2 方程和边界条件
交流情况下,假设材料特性和外加电压不随时间改变,则绝缘内的电场为稳态分布,即在频域内求解二维平面内电流守恒问题,可用下述方程描述:
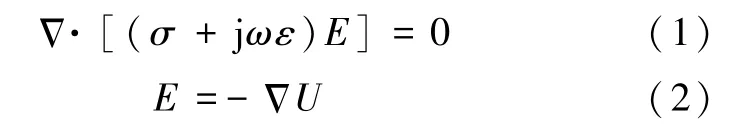
式中:σ为电导率,S·m-1;ε为介电常数;ω为角频率,rad·s-1;E为求解域内各点电场,V·m-1;U为电位,V。
在几何建模中,涉及的材料有半导电屏蔽、主绝缘、空气等3 种,由于半导电屏蔽的电导率远高于主绝缘和空气,因此可以忽略屏蔽内的电场,此时求解域可以排除半导电屏蔽层,而将半导电屏蔽界面视为求解域边界。在电缆结构中,绝缘屏蔽半导电层与缓冲层、金属护套为良好接触,可以视为接地边界;导体屏蔽半导电层与导体良好接触,可以视为电位边界。因此,模型的的边界条件为

式中,Vinsem为导体半导电屏蔽与绝缘界面的电位,V;Voutsem为绝缘半导电屏蔽与绝缘界面的电位,V;U0为导体对地电压,V。
2 模型的求解
从结构上看,电缆可以简化为同轴圆柱体绝缘结构,当绝缘为无缺陷的理想电介质时,电场沿电缆半径方向,其内部场强分布为
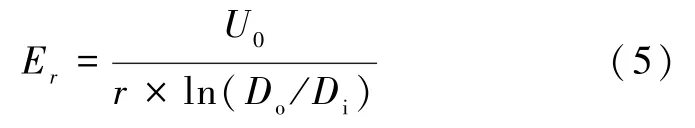
式中,Er为绝缘层内距电缆轴心为r处的电场强度,kV·mm-1;Do为导体屏蔽外径,mm;Di为绝缘外径,mm。
由式(5)计算可知,电缆绝缘层内最大场强位于导体屏蔽与绝缘交界面,最小场强位于绝缘屏蔽与绝缘交界面。因此各类缺陷导致的畸变电场最大值与缺陷在绝缘内的位置以及主绝缘的尺寸均有关系。然而,由于高压电缆绝缘内的缺陷几何尺寸非常小,缺陷也仅能影响缺陷附近极小范围内的电场分布。因此特定的缺陷形态对电场分布的影响程度应和缺陷所处位置及主绝缘尺寸等因素无关,为此定义电场畸变率(DR)为缺陷处畸变电场(E)与缺陷处平均电场(Eav)的比值,见式(6)。

故障通常在电场畸变最大位置产生,因此需要关注最大电场畸变率,见式(7)。
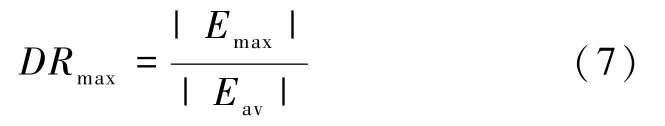
考虑到缺陷对电场分布的影响范围很小,缺陷处平均电场Eav在数值上近似等于无缺陷的理想绝缘在同一位置处的电场大小,可以通过式(5)计算。
由仿真计算方程和边界条件的特性可知,电位边界U0取值是常数,求导后并不影响电场。Eav则起到了归一化系数的作用,消除了绝缘内电场分布不均匀性的影响。因此由式(7)计算得到的最大电场畸变率DRmax与U0和Eav取值无关,仅由缺陷的具体形态确定。根据式(7)计算了不同电压等级的高压电缆绝缘内直径为50 μm 的圆形微孔的最大电场畸变率,结果见表1。

表1 高压电缆绝缘圆形微孔(ϕ50 μm)的最大电场畸变率
由表1 可知,对于绝缘内微米级别的缺陷,最大电场畸变率仅取决于缺陷形态,与缺陷所处位置、绝缘的尺寸以及导体电压几乎无关。因此可以用最大电场畸变率来表征缺陷形态对电场畸变的影响程度。
3 缺陷模型的典型仿真结果
以导体截面2 500 mm2的500 kV 电缆的结构参数建立主绝缘的几何模型,导体屏蔽外径取67 mm,绝缘外径取129 mm,导体对地电压U0取290 kV。
以长轴长度a为50 μm,短轴长度b为25 μm,长轴与电场方向的夹角θ分别取0°和90°,建立微孔几何模型,用有限元法计算微孔位于绝缘中心时,微孔附近的电场畸变率分布,典型计算结果见图5。

图5 微孔型缺陷电场畸变率分布的典型计算结果
由图5 可知,微孔内部电场畸变率最大,电场畸变导致微孔上方和下方电场被加强,微孔左右两侧电场被削弱。微孔长轴与电场方向垂直时的最大电场畸变率显著高于长轴与电场方向平行时的情况。
以突起高度H为50 μm,突起宽度L为200 μm,曲率半径R为30 μm,建立界面突起的几何模型,分别计算绝缘进入屏蔽突起和屏蔽进入绝缘突起附近的电场畸变率分布,典型的计算结果见图6。

图6 界面突起型缺陷电场畸变率分布的典型计算结果
由图6 可知,从绝缘进入屏蔽的突起,电场畸变率最大出现在突起界面与基底平面交界处,交界处附近电场被加强,突起顶部附近电场被削弱;从屏蔽进入绝缘的突起,电场畸变率最大处位于突起中部,突起顶部的电场被加强,突起两侧电场被削弱。
4 形态参数对缺陷电场畸变的影响
4.1 内部微孔
固定微孔长轴与电场方向平行,即θ=0°,并取a∶b分别为2 ∶1,3 ∶2 和1 ∶1,改变a的取值从10 μm 到90 μm,对每一组参数值建模进行仿真计算,结果见图7。
由图7 可知,当a∶b恒定时,最大电场畸变率几乎不随a取值变化而改变,说明形状相同时,微孔大小对电场分布基本无影响;当a∶b下降时,最大电场畸变率明显增大,说明微孔形状对电场分布影响显著。
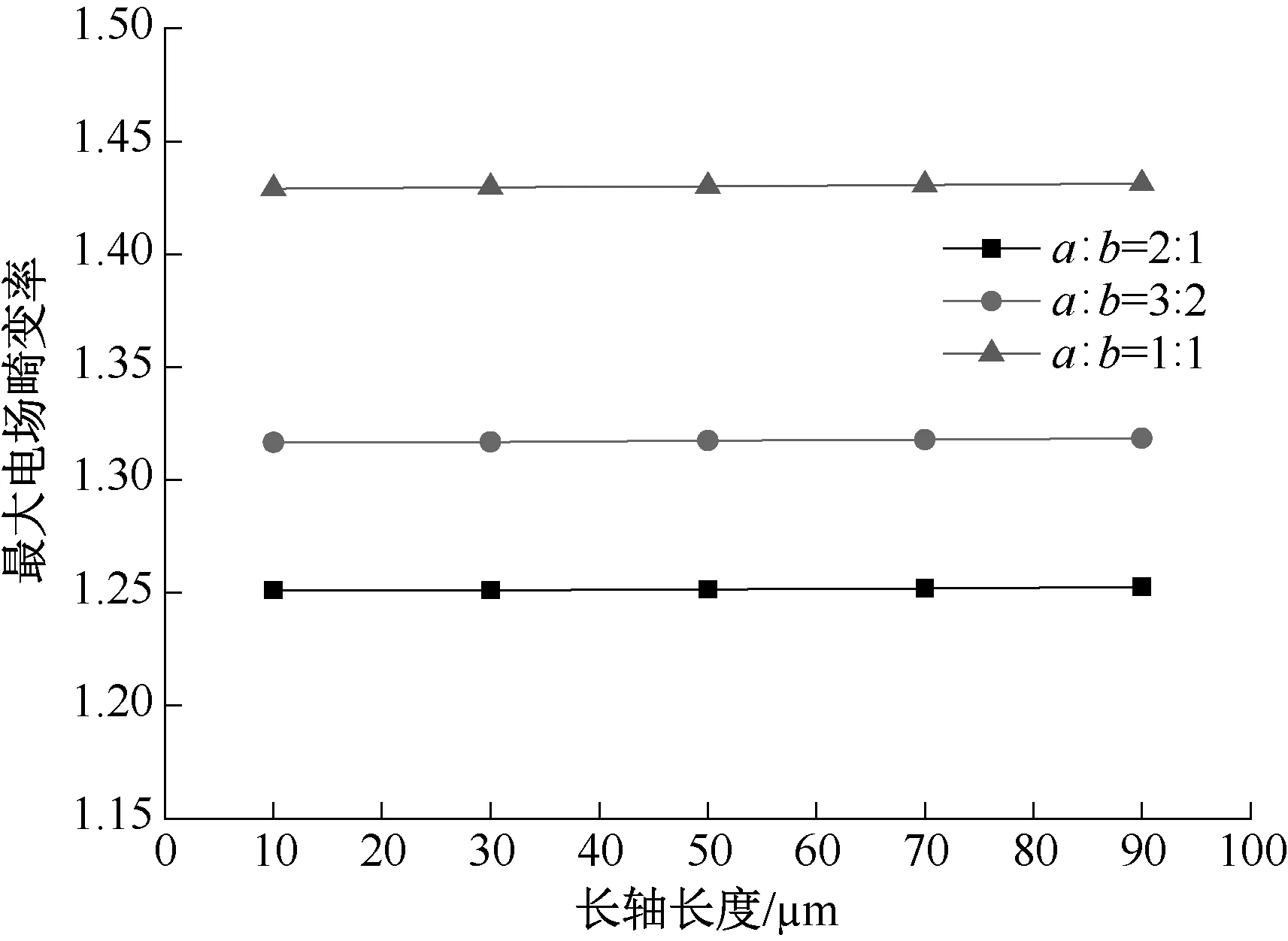
图7 微孔大小对电场分布的影响
固定a为50 μm,b为25 μm,当θ由0°~180°时,对每一组参数进行仿真计算,结果见图8。
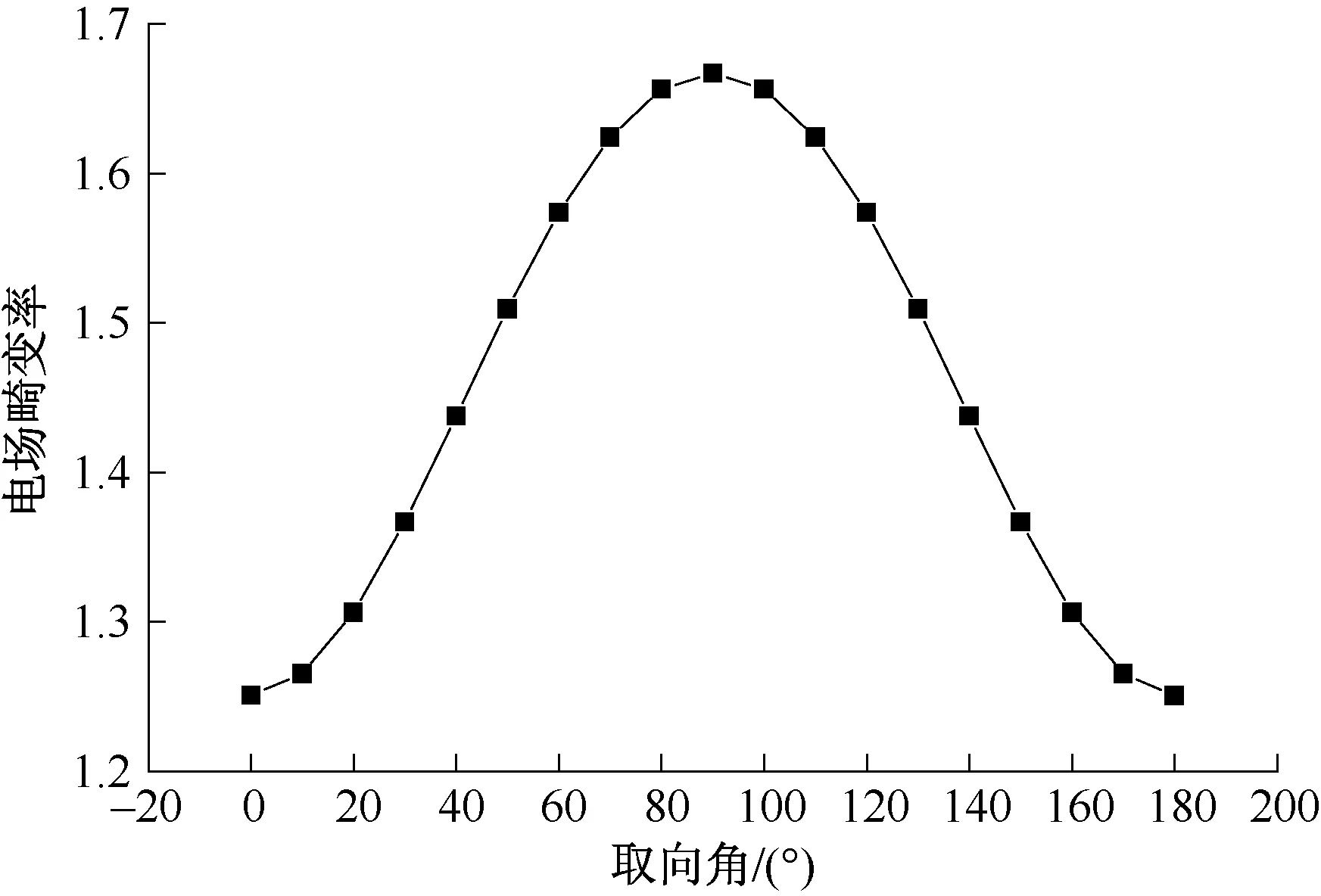
图8 取向角对电场分布的影响
由图8 可知,最大畸变率在取向角90°时取得最大值,在0°或180°时取得最小值,说明微孔取向对电场分布有显著性影响。当微孔形状一定时,若微孔长轴垂直于电场方向,电场畸变率最大;若微孔长轴平行于电场方向时,电场畸变率最小。
固定b为10 μm,改变a的取值从10 μm 到90 μm,分别对θ为0°和90°两种情况进行计算,结果见图9。
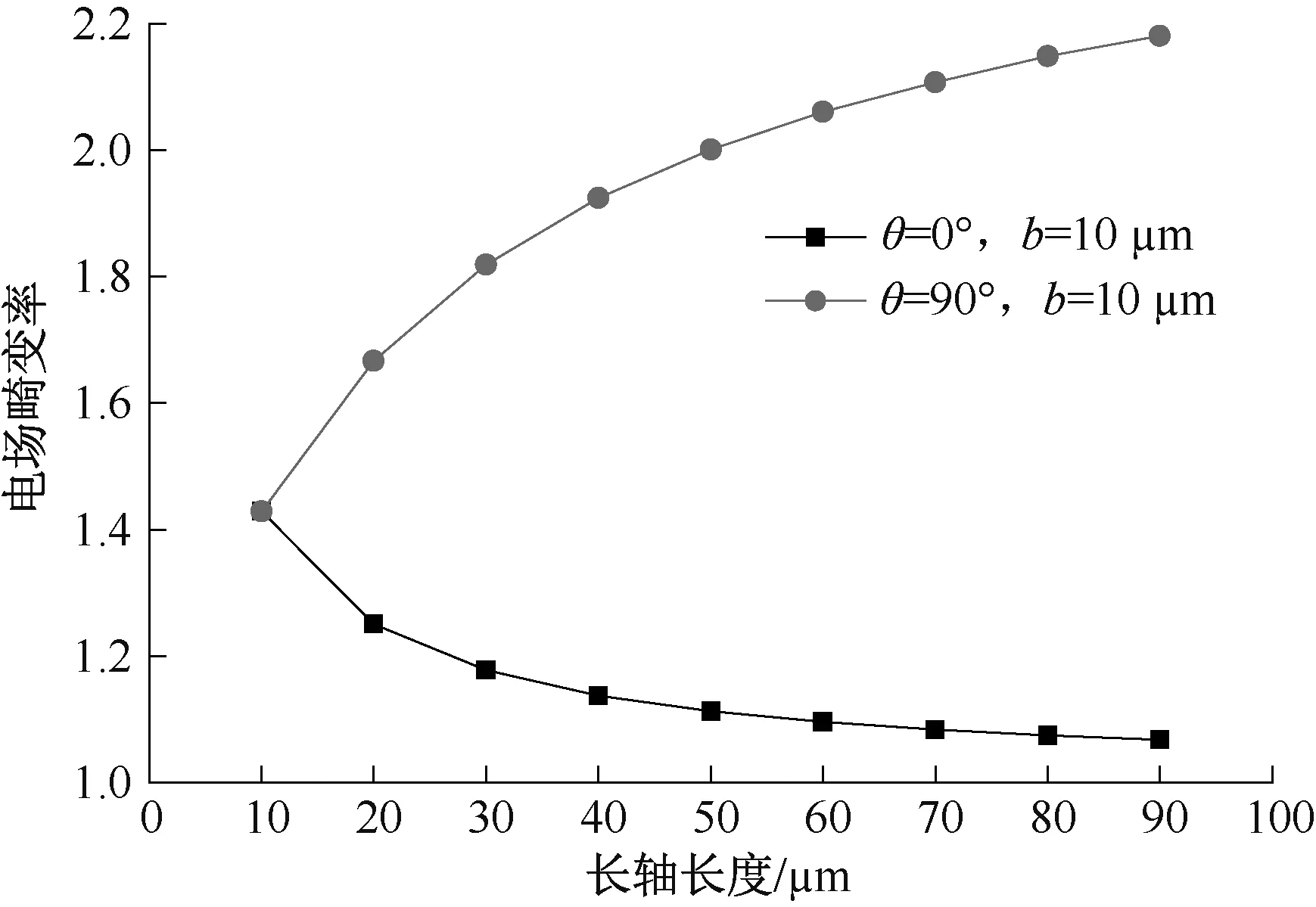
图9 微孔在不同方向上投影长度对电场分布的影响
由图9 可知,当θ=0°时,最大电场畸变率随a的增大而减小;当θ=90°时,最大电场畸变率随a的增大而增大。说明微孔造成的电场畸变程度与微孔在垂直于电场方向的投影长度呈正相关,与微孔在平行于电场方向的投影长度呈负相关。
4.2 界面突起
由于同形态的界面突起在导体屏蔽处和绝缘屏蔽处产生的电场畸变率基本相同,因此分析时不再考虑突起位置的影响。
改变H取值从25 μm 到100 μm,计算不同L、H、R下两类界面突起的最大电场畸变率,相似形态界面突起大小对电场畸变率的影响见图10。
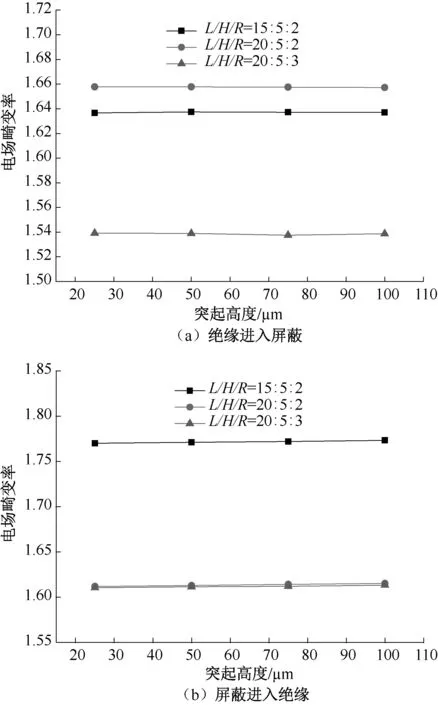
图10 相似形态界面突起大小对电场畸变率的影响
由图10 可知,确定L、H、R三者的比例后,无论突起是从绝缘进入屏蔽还是从屏蔽进入绝缘,最大电场畸变率几乎不随界面突起高度取值大小改变,说明在形状相同时,界面突起的大小对电场分布无影响。
取L=250 μm,H=50 μm,改变曲率半径R的取值从10 μm 到90 μm,曲率半径对电场畸变率的影响见图11。
由图11 可知,对于从绝缘进入屏蔽的突起,最大电场畸变率随曲率半径R增大显著降低;对于从屏蔽进入绝缘的突起,最大电场畸变率则几乎不随曲率半径R的变化而变化。
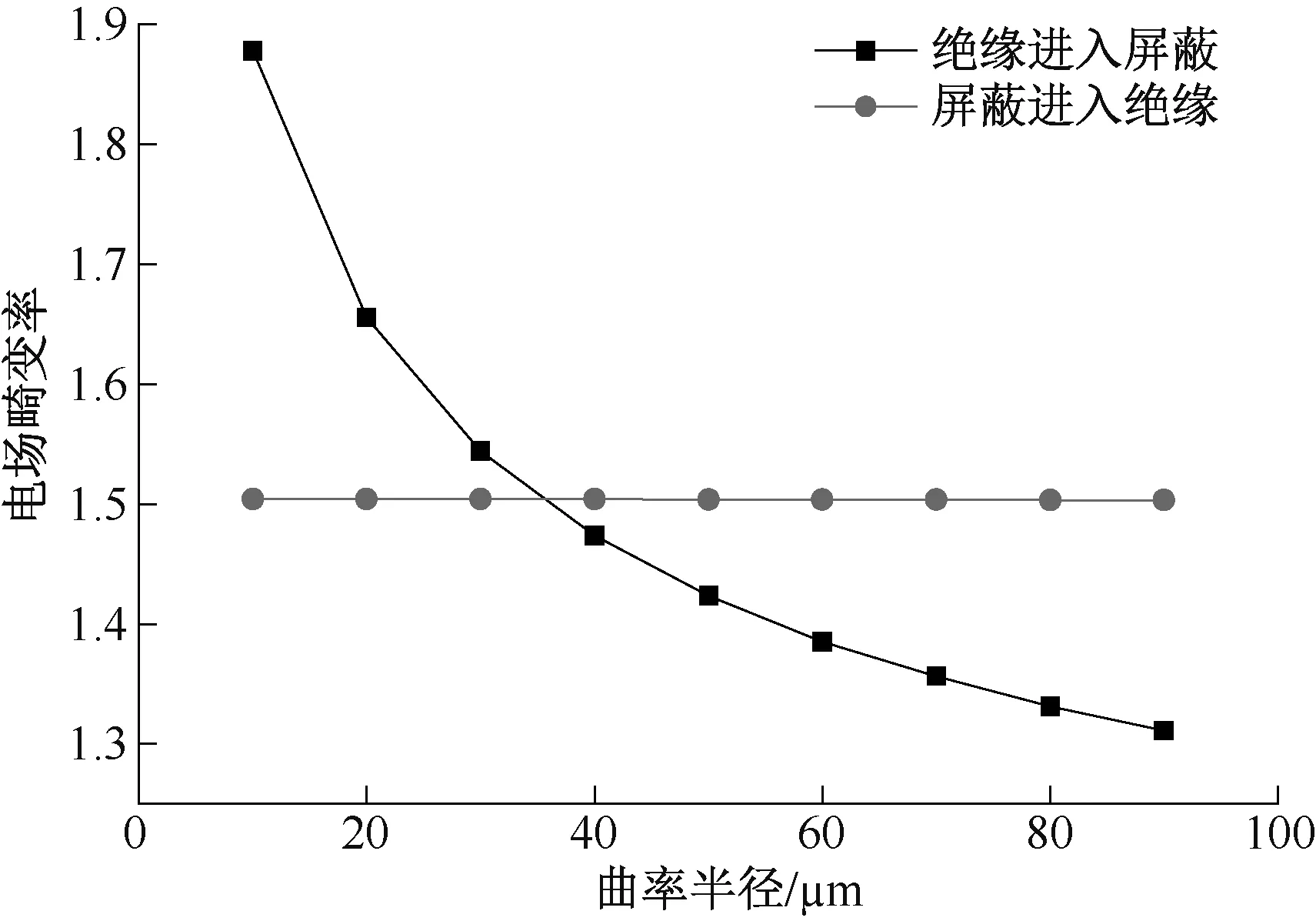
图11 突起界面与平面交界处曲率半径对电场畸变率的影响
取R=30 μm,L=250 μm,改变突起高度H的取值从10 μm 到90 μm,突起界面高度对电场畸变率的影响见图12。
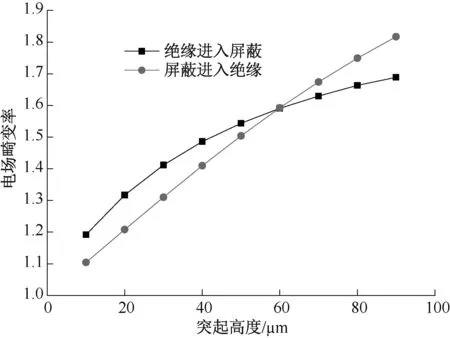
图12 突起界面高度对电场畸变率的影响
由图12 可知,两类突起的最大电场畸变率均随H增大而上升。比较而言,当突起从屏蔽进入绝缘时,最大电场畸变率随H上升趋势更为明显。
取R=30 μm,H=50 μm,改变突起宽度L的取值从150 μm 到500 μm,突起界面宽度对电场畸变率的影响见图13。
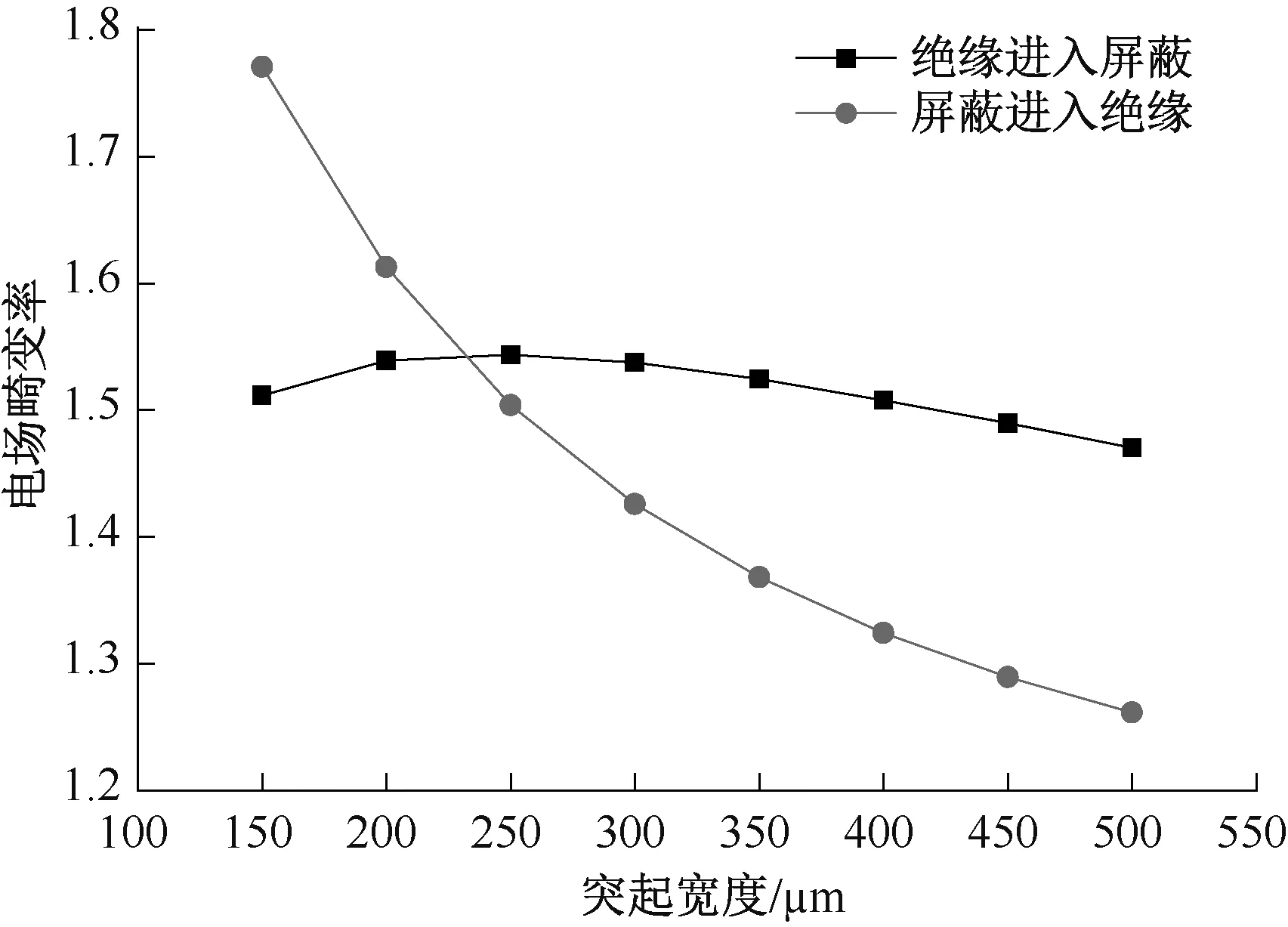
图13 突起界面宽度对电场畸变率的影响
由图13 可知,对于绝缘进入屏蔽的突起,最大电场畸变率随L增大时先小幅增大,后逐渐减小,但变化趋势不明显。对于屏蔽进入绝缘突起,最大电场畸变率随L的增大显著减小。
5 结论
本工作对高压电缆主绝缘内的典型缺陷建立二维仿真模型,采用有限元仿真计算了绝缘内部微孔和半导电屏蔽-绝缘界面突起的电场分布,仿真结果表明:
(1)电缆主绝缘内微孔和界面突起缺陷造成的电场畸变仅取决于缺陷的形状。当形状相同时,小尺寸缺陷造成的电场畸变程度与大尺寸缺陷相当,缺陷尺寸越大,造成的电场畸变范围越大。
(2)微孔缺陷造成的电场畸变程度主要取决于微孔在平行电场方向的投影长度和在垂直电场方向的投影长度间的比例,比例越大,电场畸变程度越小。
(3)当界面突起方向为从绝缘进入屏蔽时,电场畸变率最大处位于突起界面与基底平面交界处。通过增大交界处的曲率半径和减小突起高度,可有效降低电场畸变的程度。界面突起宽度的变化对电场畸变的影响不大。
(4)当界面突起方向为从屏蔽进入绝缘时,电场畸变率最大处位于突起顶部。通过增大突起宽度和减小突起高度,可有效降低电场畸变的程度。
