变速引纬规律驱动下剑带变长度非线性振动建模及其响应
2022-12-23袁汝旺车一骋
袁汝旺, 车一骋
(1.天津工业大学 机械工程学院, 天津 300387; 2.天津工业大学 天津市现代机电装备重点实验室, 天津 300387)
剑杆织机广泛用于棉、麻、毛、丝等多种纤维材料织造,其织造速度可达650 r/min以上。剑带常用驱动方式有共轭凸轮[1]、空间四连杆[2]与变导程螺杆[3]等。不同剑带驱动形式下的变速引纬规律存在初始加速[4]、加速度峰值等差异,并对纬纱飞行稳定性与工艺存在一定影响。
目前,国内外学者主要研究剑带引纬运动规律、剑带驱动机构及其动态特性等[1-3]。同时高速织机剑带振动、剑头磨损[5]和纬纱断头等问题亦成为国内外研究热点。剑带由往复变速摆动的传剑轮驱动并沿导轨作周期性伸缩运动,潘宏根[6]基于轴向运动梁方法建立定长度下匀速运动剑杆的自由振动模型,得出纵向振动对引纬位移影响有限的结论。马国良[7]等探讨不同轴向运动速度和末端质量作用下变长度梁自由振动特性。轴向运动梁的分析方法主要基于数值分析法,如Wang[8]与Piovan[9]等应用有限变形理论研究轴向运动梁振动,李成[10]、Chen[11]和吴娟[12]等对轴向运动系统的响应分别利用解析法与多尺度法分析法。
本文从剑带引纬规律出发,建立基于余弦级数的变速引纬规律设计模型,适应不同引纬规律需求。并用有限元法建立变长度非线性受迫振动模型,进而分析不同引纬规律下工艺特性及其剑带振动对引纬的影响,为高速化引纬以及引纬过程的稳定性设计提供理论参考及建议。
1 引纬模型
1.1 引纬工艺分析
剑杆引纬通常以双侧剑杆中央交接的形式完成[13],图1示出单侧剑杆运动原理。剑带端部安装剑头,传剑机构驱动剑带轮3绕其回转中心变速往复摆动,剑带轮3带动剑带2和剑头1作往复变速直线运动。
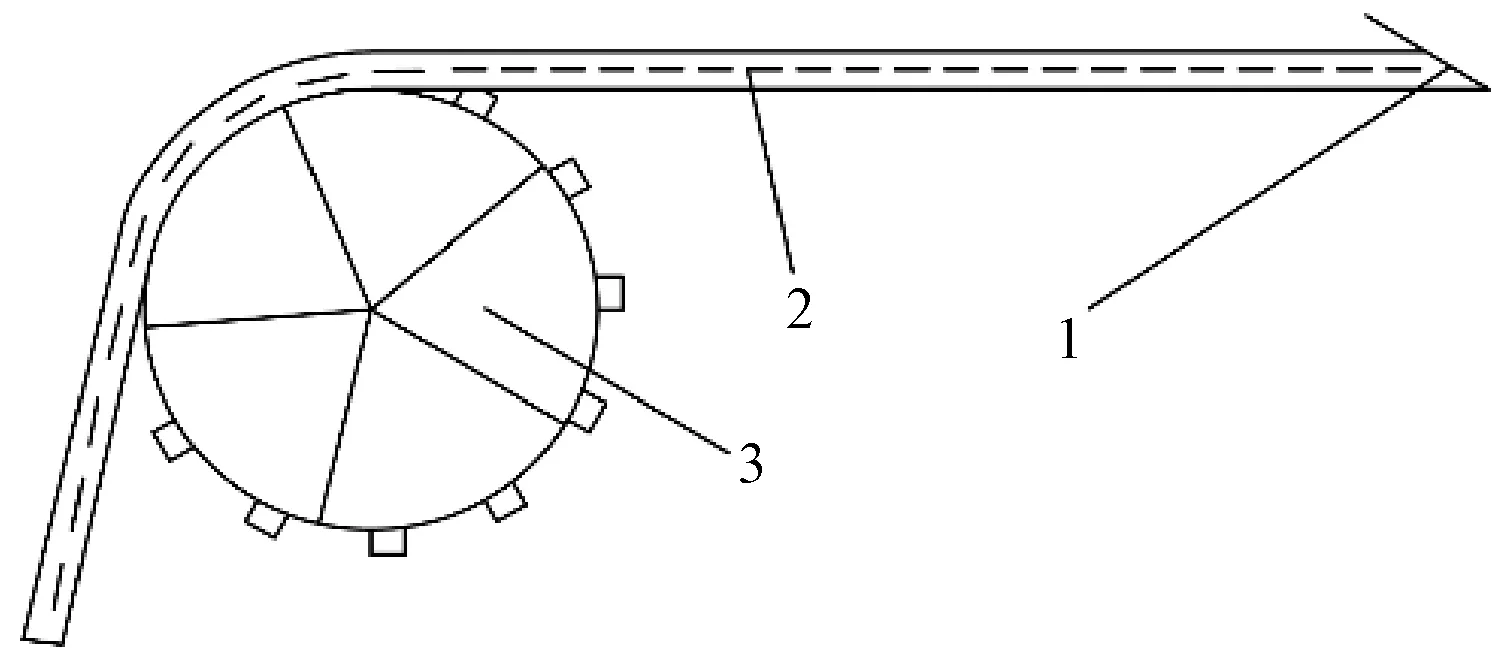
1—剑头;2—剑带;3—剑带轮图1 剑带引纬简图Fig.1 Sketch of weft insertion of sword belt
图2示出剑头位移变化情况。在一个织造周期内剑头连续运动,当θ=0时,剑头开始运动;当θ=θs时,剑头运动至A点并握持纬纱;当θ=θk时,剑头握持纬纱共同运动至B点,即梭口位置;当θ=θz时,剑头运动至C点,动程达到最大且开始回退,并在θz=180°附件完成纬纱交接;θ=θv时,剑头退出梭口,且剑头进出梭口时间θk与θv关于θz=180°对称;当θ=360°时,剑头回退至初始位置。在引纬的过程中,剑头进梭口时间θk、纬纱交接时间θz、剑头退出梭口时间θv等为重要工艺参数,对纬纱的运动特性和交接的平稳性至关重要。
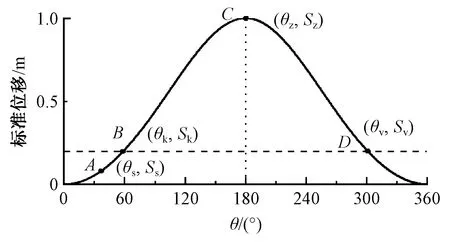
图2 剑头位移示意图Fig.2 Sword head displacement diagram
根据织机参数可知剑头动程最大动程Smax为
Smax=0.5W+B+0.5D
(1)
式中:W为织物幅宽,m;B为幅外动程,m;D为纬纱交接冲程,m。
1.2 变速引纬模型
为满足不同剑带驱动形式下剑带运动特性与工艺,基于余弦级数建立变速引纬位移方程为
(2)
式中:S为剑带位移,m;Smax为引纬最大动程,m;θ为织机主轴转角,(°);θ0为最大动程所对应主轴转角,通常θ0=180°;ak(k=0,1,2…n)为余弦项系数。
式(2)对时间求导可得引纬速度与加速度:
(3)
式中,ω为织机主轴角速度,(°)/s。
令H=θ/θ0,将剑杆引纬位移进行归一化处理可得:
(4)
f(H)对主轴转角θ求导可以得标准速度以及标准加速度f′(H),f″(H):
(5)
系数ak采用待定系数法确定,将引纬位移、速度以及加速度参数化,引纬过程中θ=0、θs、θk等时所对应的f(H)、f′(H)和f″(H)为参数化边界条件,如当取θ0=180°时,满足进梭口角θs=35°的边界条件参数化可表示为f(θs/θ0)=f(35/180)=B/Smax。因此得到n+1个参数化边界条件的等式即可求解。
2 剑带振动模型
假定匀质剑带,对于连续体的分析采用有限元法进行离散。驱动机构从左端对剑带施加时变驱动力F(t),使其完成变速引纬,在引纬过程中剑带长度不断发生变化。图3示出剑带不同时间下纵向振动的有限元模型,划分n个单元则有n+1个节点,且单元长度l(t)随着时间而变化。
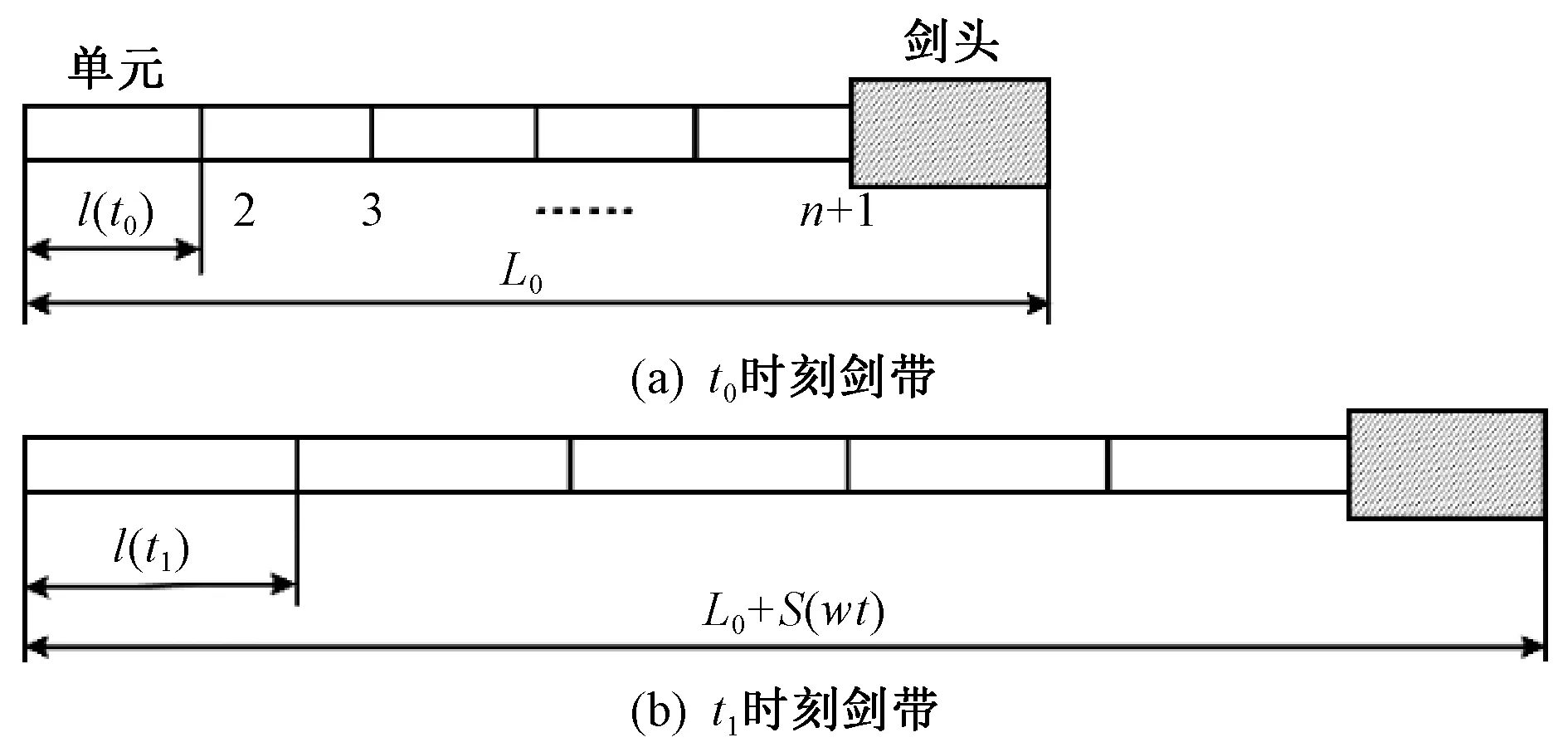
图3 不同时刻剑带有限元模型Fig.3 Finite element model of sword belt at different times
剑带长度与引纬位移S的关系为
L(t)=L0+S(θ)=L0+S(ωt)
(6)
式中:L0为剑带起始长度,m;t为时间,s。
在变速引纬规律下,时变驱动力F(t)为此振动系统的主要激励。其与引纬加速度S″的关系为
F(t)=(m+ρAL(t))S″(ωt)
(7)
式中:m为端部质量即剑头,kg;ρ为剑带密度,kg/m3;A为剑带截面积,m2。
2.1 剑带单元分析
图4示出剑带单元的分析简图,当划分为n个单元时,单元长度l(t)=L(t)/n与引纬时间有关。节点1,2的位移与力分别为u1(t),u2(t)和F1(t),F2(t);f(x,t)表示x处应力。
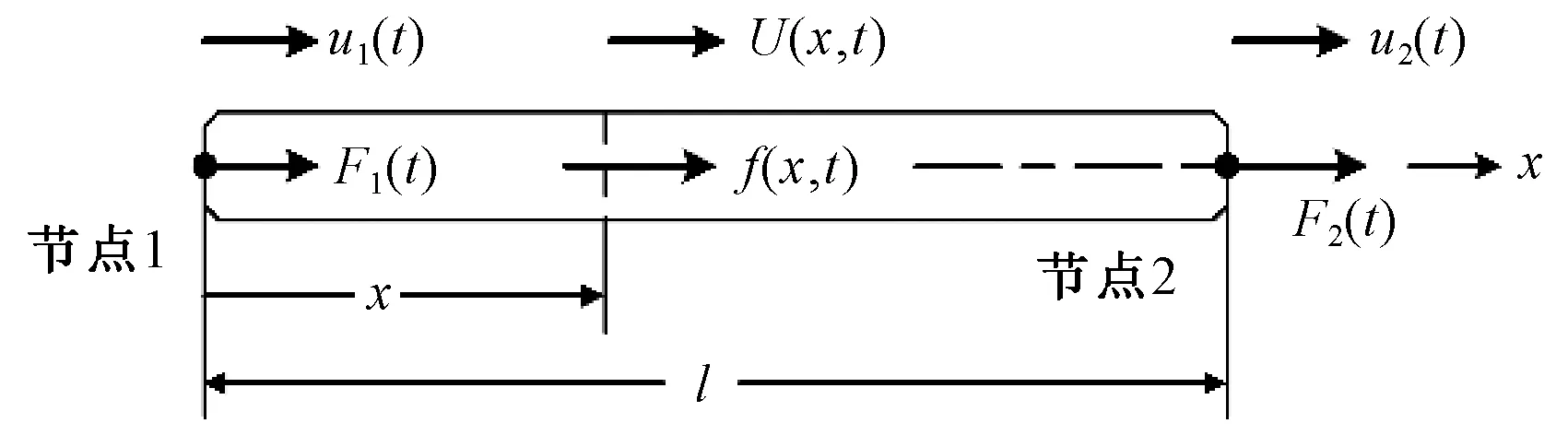
图4 单元受力变形图Fig.4 Deformation diagram of unit stress
以u1(t),u2(t)构成单元坐标Ue=[u1,u2]。单元形状函数取Ne=[N1,N2],其中N1=1-x/l,N2=x/l。单元纵向位移Ue(x,t)=NeUeT。
单元为连续体,其动力学本构关系采用Kelvin模型,如图5所示。
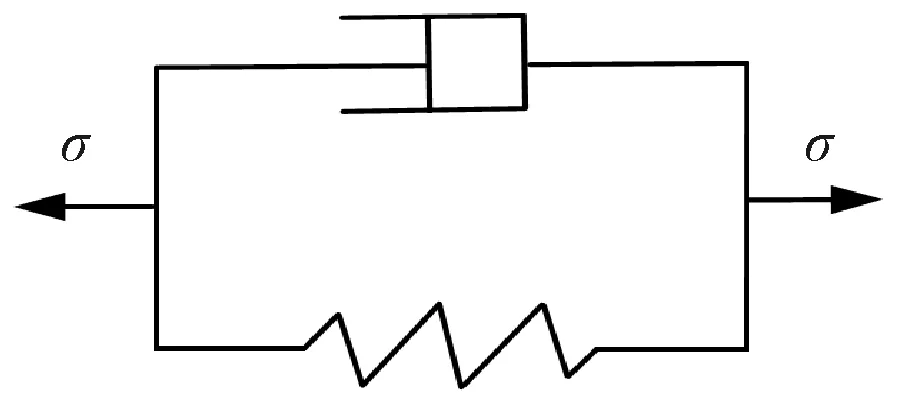
图5 单元本构模型Fig.5 Element constitutive model
剑带单元本构方程可表示为
(8)
式中:σ为应力,Pa;E为剑带弹性模量,Pa;ε为应变量;c为阻尼系数。
由本构方程提取出其微分算子E*表示为
(9)
进行能量分析,单元动能Te与势能Ve为
(10)
(11)
式中:Me、Ke、Ce分别表示单元质量阵、刚度阵、阻尼矩阵。其各值根据式(10)、(11)中积分式子化简整理可得式(12)。
(12)
剑带端部即第n单元受剑头质量m影响,可进行质量集中处理,其Me附加剑头质量可改写为
(13)
由Dalembert原理可得各节点等效激应力Fe为
(14)
变速引纬下,剑带仅一端受到时变驱动力F(t),因此只有单元1具有等效激应力Fe=[F(t) 0]。
由式(12)可知,此系统中的质量、刚度以及阻尼项均带有可变长度l(t)项,具有非线性;而剑带端部节点受时变驱动力F(t)激励,因此系统为变长度非线性受迫振动系统。
2.2 剑带振动方程
剑带由n个单元组成,且通过相应节点连接成一整体。各节点质量、刚度、阻尼叠加,可得整体质量矩阵M,整体刚度矩阵K和整体阻尼矩阵C。
(15)
式中:i,j为下标,表示矩阵第i行第j列中元素。而矩阵K、C的叠加形式由M同理可得。
整体剑带的动势Q表示为动能与势能的差值:
(16)
式中,U为整体节点向量,U=[u1,u2,…,un]。
根据拉格朗日能量法推导动力学方程为
(17)
将式(7)、(15)、(16)代入式(17)中,得到剑带最终的振动方程组:
(18)
对式(18)采用四阶龙格库塔求解[14],即可得各节点ui对应的位移、速度以及加速度。三者产生的波动量分别用Δx(θ),Δx′(θ),Δx″(θ)表示,表示剑头节点un+1运动量与理论量S的差值,如Δx(θ)=un+1(θ)-S(θ),依次可知Δx′(θ),Δx″(θ)。
3 结果与讨论
考虑工程应用背景,本文选取实际剑杆织机各个参数带入剑带振动方程,讨论不同引纬加速度参数条件下的工艺性与剑带振动的影响。织机幅宽W=2 800 mm,幅外动程B=165.5 mm,剑头交接冲程D=90 mm,织机主轴转速w=550 r/min,剑带密度ρ=1 900 kg/m3,弹性模量E=8.1GPa,截面积A=7.5×10-5m2,剑头质量m=0.61 kg,阻尼系数的选取较为困难,因而参考文献[15]中,取阻尼系数c=122 Pa·s。
3.1 不同引纬参数下工艺性
在幅宽、转速等参数相同的情况下,讨论不同起始加速度参数f″(0)下的引纬工艺性,图6示出引纬负向加速度峰值f″(1)=-0.65条件下,f″(0)=0、0.2、0.4时引纬规律运动特性。
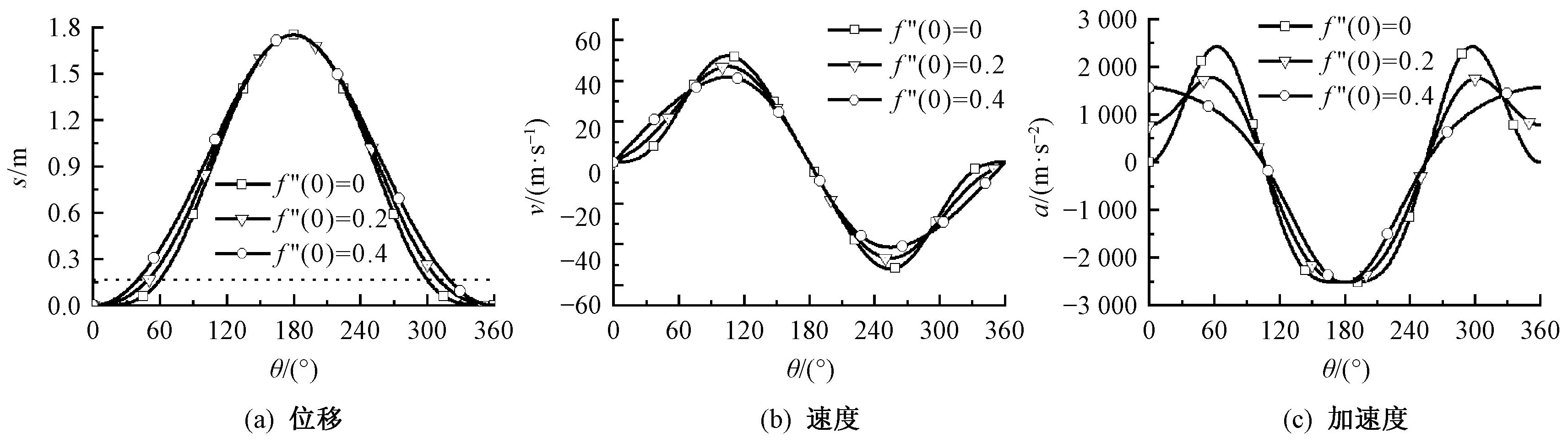
图6 不同f″(0)下的引纬运动特性Fig.6 Motion characteristics of weft insertion with different f″(0). (a) Displacement; (b) Speed; (c) Acceleration
由图6可知,3种运动规律具有相同的负向加速度峰值;随着f″(0)的增加,剑带进入梭口所对应的主轴转角θk、速度峰值vmax和加速度峰值amax逐渐减小,f″(0)=0.4时加速度变化最为平缓,但其具有初始加速度,存在柔性冲击,起始段具有较差引纬稳定性。
初始加速度f″(0)越小,剑头进梭口角越大,幅内引纬时间越短,打纬和开口运动时间越长,此时剑带速度与加速度峰值较大,不利于引纬平稳性;同理,当f″(0)越大,剑头进梭口角越小,幅内引纬时间越长,因此打纬和开口分配时间越短,造成打纬等工艺步骤载荷偏大。表1示出多个f″(0)取值下引纬特征值。进梭口角θk改变约20°,速度峰值vmax下降约30%,加速度峰值amax减小约35%。
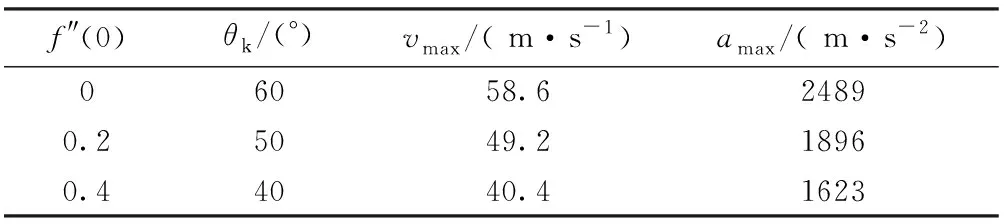
表1 不同f″(0)下引纬特性值Tab.1 Weft insertion characteristic values under different f″(0)
引纬加速度参数f″(0)对工艺影响显著,本模型能够充分反应引纬中的运动规律变化对工艺的影响,对f″(0)的调整可改变θk约20°与减小vmax约30%,因此在织造过程中,根据打纬、引纬和开口工艺需求,应合理选择初始加速度。
3.2 不同引纬加速度参数下剑带振动分析
3.2.1 位移响应
图7示出f″(1)=-0.65条件下f″(0)=0、0.2、0.4时剑带振动引起的位移波动Δx。由图可知,Δx呈周期性变化,负向最大波动量-Δxmax均发生在纬纱交接位置附近,约为-0.6 mm。当f″(0)增加时,正向最大波动量Δxmax不断减小,其发生位置向周期起始点发生偏移。f″(0)=0时,Δxmax=0.53 mm,而当f″(0)=0.4时,Δxmax=0.35 mm,振幅减小约34%。
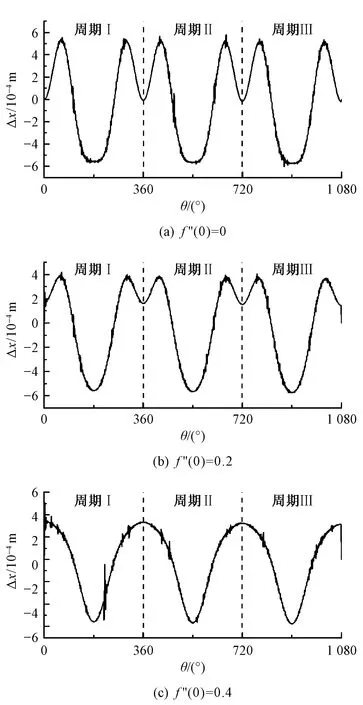
图7 不同f″(0)下的位移响应Fig.7 Displacement response under different f″(0)
振动对位移的影响主要为驱动力引起强迫振动,材料自由振动所致影响很微小。且振幅相对于剑头位移总量仅占约0.04%。剑带振动对位移的影响不大,设计引纬规律可忽略振动对位移的影响。
3.2.2 速度响应
图8示出f″(1)=-0.65条件下取f″(0)=0、0.2、0.4时剑带的速度波动Δx′。
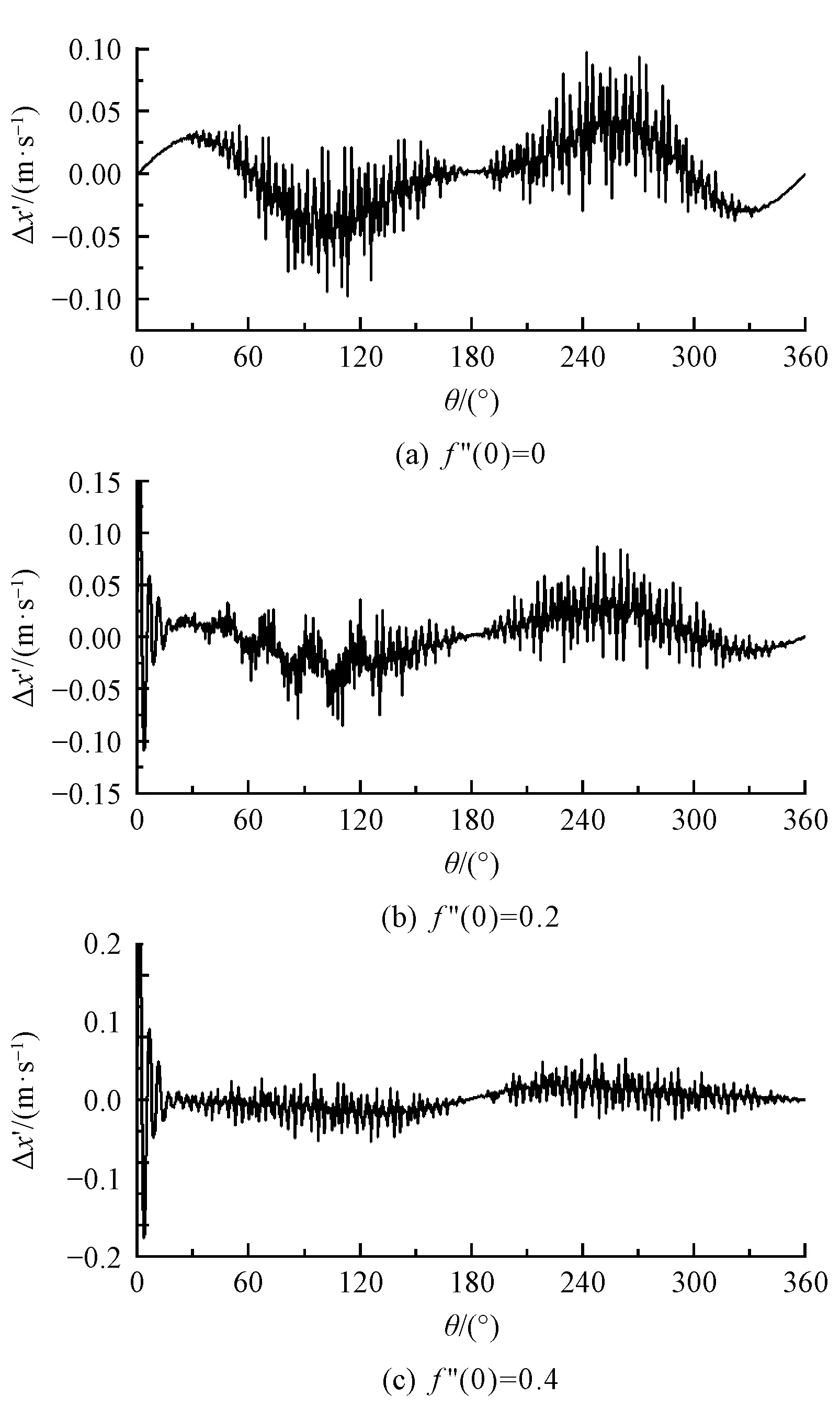
图8 不同f″(0)下的速度响应Fig.8 Speed response under different f″(0)
在主轴转角30°~360°区间内,随着f″(0)增大,速度波动Δx′将会小幅减小,当f″(0)=0时,其最大波动为0.11 m/s,当f″(0)=0.4时,其值降为0.06 m/s,两者差距仅为0.05 m/s。主轴转角在0°~30°区间内时,随着f″(0)的增加,速度波动将大幅增加,在f″(0)=0.4时,主轴转角为0°位置速度波动最大,其值约为0.25 m/s,而f″(0)=0时其波动约为0,两者差距可达0.25 m/s。起始加速度f″(0)不同主要影响剑带在织机主轴转角0°~30°区间内的速度响应。
振动对速度的影响为驱动力引起低频强迫振动与材料高频自由振动的耦合。速度最大波动约为引纬设计最大速度的0.6%。剑带振动对速度的影响有限,设计引纬规律时可忽略振动对速度的影响。
3.2.3 加速度响应
图9示出f″(1)=-0.65时下取f″(0)=0、0.2、0.4时剑带的加速度波动。由图可知,纬纱交接附近产生的波动均为最小;主轴转角90°附近,加速度波动达到局部最大;随着f″(0)增大,织机主轴转角在0°~30°区间内加速度波动加剧,因而剑带抖动剧烈。当f″(0)=0时,其加速度波动接近0;而当f″(0)=0.4时,最大加速度波动达到1 500 m/s2左右,其值约为引纬加速度峰值的53%,综合图6可知,θ=0附近波动加速度峰值最大,可达约3 500 m/s2,其为相应位置波动量与加速度值相加,因而可增加加速度峰值约40%,若以加速度引起的惯性力代替剑带内应力时,剑带内应力峰值增加约40%,增加断带可能。
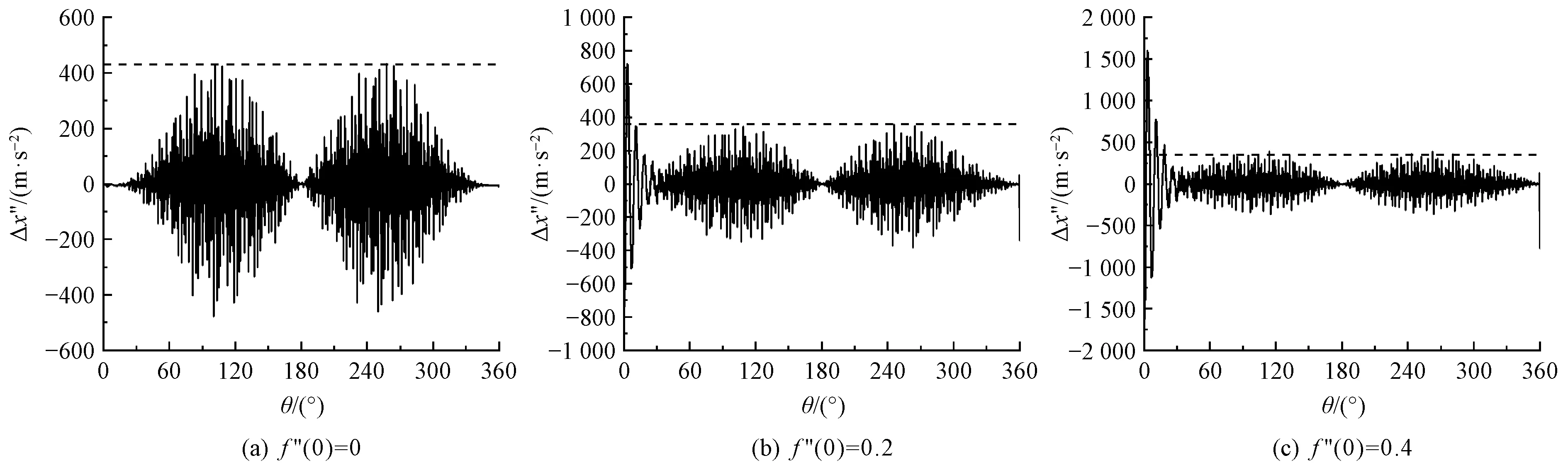
图9 不同f″(0)下的加速度响应Fig.9 Acceleration response under different f″(0)
图10示出在f″(0)= 0条件下取f″(1)=-0.65、-0.45、-0.25时加速度误差。可知,起始段与纬纱交接附近的波动均接近0;但随着f″(1)取值增加,偏差峰值所对应主轴转角θmax不断减小。表2示出不同f″(1)取值时织机主轴位于θmax、θk和θs处剑带的加速度偏差。随着f″(1)取值增加,织机主轴位于θk和θs处加速度的波动增大,对纬纱的应力波动加剧;当f″(1)取值由-0.65增加至-0.25时,θk与θs处产生的加速度波动分别增加21%与66%,不易于引纬的稳定性。
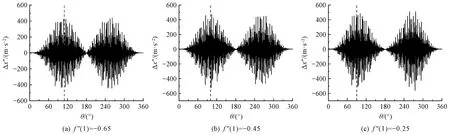
图10 不同f″(1)下的加速度响应Fig.10 Acceleration response under different f″(1)

表2 不同f″(1)下振动特性Tab.2 Vibration characteristics under different f″(1)
振动对加速度影响主要为材料自身引起自由振动,起始最大加速度波动与局部加速度波动峰值约为理论加速度峰值的50%与16%。过大的起始加速度f″(0)会引起较大的起始段振动,增加剑带断裂风险,而主轴转角在30°~360°区间内剑带振动有所减弱;同时,负向加速度峰值f″(1)使得θk、θs处加速度波动变大,纬纱应力波动增大,因此不利于纬纱握持,进而影响引纬稳定性,造成断纬等危害。
通过对剑带振动的讨论,可见不同加速度参数下的剑带振动对引纬有不同的影响,剑带纵向振动对位移与速度的影响较小,与文献[12]中剑杆纵向振动对引纬位移的影响有限的结论具有一致性。但其对引纬加速度影响显著,过大f″(0)将增加剑带应力峰值近40%等,而过大f″(1)将增大握持纬纱与进梭口处振动,纬纱应力波动加剧,影响引纬稳定性。
4 结 论
1)建立基于余弦级数的变速引纬规律参数化模型,通过调节初始加速度参数分析引纬规律运动特性及工艺性,得到加速度参数f″(0)对引纬工艺的影响显著,f″(0)由0增加到0.4时,将减小进梭口角θk约20°与速度峰值vmax约30%。
2)基于有限元法建立剑带变长度非线性受迫振动模型,分析不同加速度参数下剑带纵向振动动态响应与对引纬工艺影响,结果表明:剑带振动对位移与速度的影响较小,但其对引纬加速度影响显著;主轴转角在0°~30°范围内初始加速度f″(0)取值对加速度波动影响最大。过大f″(0)将增加剑带内应力峰值约40%;过大f″(1)将增大握持纬纱与进梭口处振动,加速度波动变大,纬纱应力波动增大。
3)剑带运动初始加速度与纬纱交接附近加速度峰值是影响引纬工艺的关键参数,合理设置二者取值,协调打纬、引纬与开口工艺时序与运动需求,为剑杆织机产品系列化设计提供理论参考依据。
