羽绒制品热传递的有限元仿真

2022-12-23吴佳玥吴巧英

纺织学报 2022年11期

吴佳玥，吴巧英

(1.浙江理工大学服装学院，浙江杭州 310018； 2.浙江理工大学国际教育学院，浙江杭州 310018)

保暖性是决定消费者购买羽绒制品的关键因素之一。目前，羽绒制品的保暖性能主要通过织物保暖仪、暖体假人等方法测试得到[1]，由于此类方法花费时间较长、成本较高，因此通过建立数值模型，对织物热传递进行模拟已成为当下重要发展趋势[2]。目前，已有许多学者采用有限元的方法对织物的热传递性能进行了分析。早在2005年，孙玉钗等[3-4]利用有限元软件模拟纺织品的热传递过程，并得到热量传递过程中织物横截面任意位置、任意时刻温度分布情况。Muhamma等[5]提出了一种用有限元法计算织物有效导热系数和热阻的方法。Puszkarz等利用有限元法模拟分析了双层针织面料的隔热性能[6-7]、以及多层织物制成的热防护服在辐射热作用下的传热性能[8]。张艺强等[9]利用有限元法探究空气层厚度与位置对织物热传递的影响。上述研究均针对单层织物或多层织物制成的服装进行有限元仿真模拟，目前针对羽绒制品建立有限元仿真模型的研究鲜见报道，因此本文拟通过建立羽绒制品的三维模型来测试其保暖性。

另外，许多文献对羽绒保暖性影响因素进行了实验分析。丛杉等[10]选取市场中常用羽绒服面料及絮料进行保暖性实验分析，结果表明，在保暖性能方面，絮料所产生的影响比表层织物种类产生的影响大。孙莉等[11]通过正交试验，探究了影响羽绒服保暖性的因素，按影响程度从大到小排序依次为：填充密度、绗缝数量、织物。何雨[12]通过羽绒实验袋试样热阻测试，得到环境条件相同时，填充密度对羽绒试样的热阻有所影响。

因此，本文在织物热传递理论基础上，利用有限元软件对“羽绒-织物-皮肤”建立简化的三维有限元模型，模拟分析不同织物、填充密度及绗缝数量条件下，模型内部和表面的温度场分布特征，通过羽绒和织物的导热性能参数来计算羽绒的保暖性，为羽绒制品的设计优化提供参考。

1 模型传热分析

在不考虑湿传递的情况下，热量传递方式有：热传导、热对流和热辐射3种。

1.1 热辐射

在由“羽绒-织物-皮肤”组成的系统中，设定皮肤温度为实验时平板的温度36 ℃，环境温度为实验时室内温度22 ℃，皮肤热量先传递至靠近皮肤一侧的内层织物，再传递到羽绒，然后传递到远离皮肤一侧的外层织物，最后以对流换热的方式传递给外界环境，温度逐渐递减。通过实验可知，经过一段时间的热平衡后，远离皮肤一侧的外层织物平均温度逐渐升高至24 ℃左右，靠近皮肤一侧的内层织物平均温度上升至29 ℃左右，因此内层织物与皮肤的温差、内层织物与外层织物的温差、外层织物与环境之间的温差都较小，辐射传热的作用很小。

通过计算进行验证，2个系统间净热辐射的公式为

q1=εδ(T14-T24)

式中：q1为热流密度，W/m2；δ为斯提芬-波尔赫兹常数，其值为5.67×10-8W/(m2·K4)；ε为放射率，其值在(0，1)之间；T1为温度较高辐射表面温度，℃；T2为温度较低辐射表面温度，℃。

以皮肤温度与靠近皮肤一侧的内层织物为例进行热辐射估算，将T1=36 ℃，T2=29 ℃，ε取最大值1代入热辐射公式，得到其值约为0.055 W/m2，该值较小。因此为简化模型，本文研究忽略热辐射的作用，仅考虑热传导以及对流换热2种传热方式。图1为稳态热传递三维过程图。

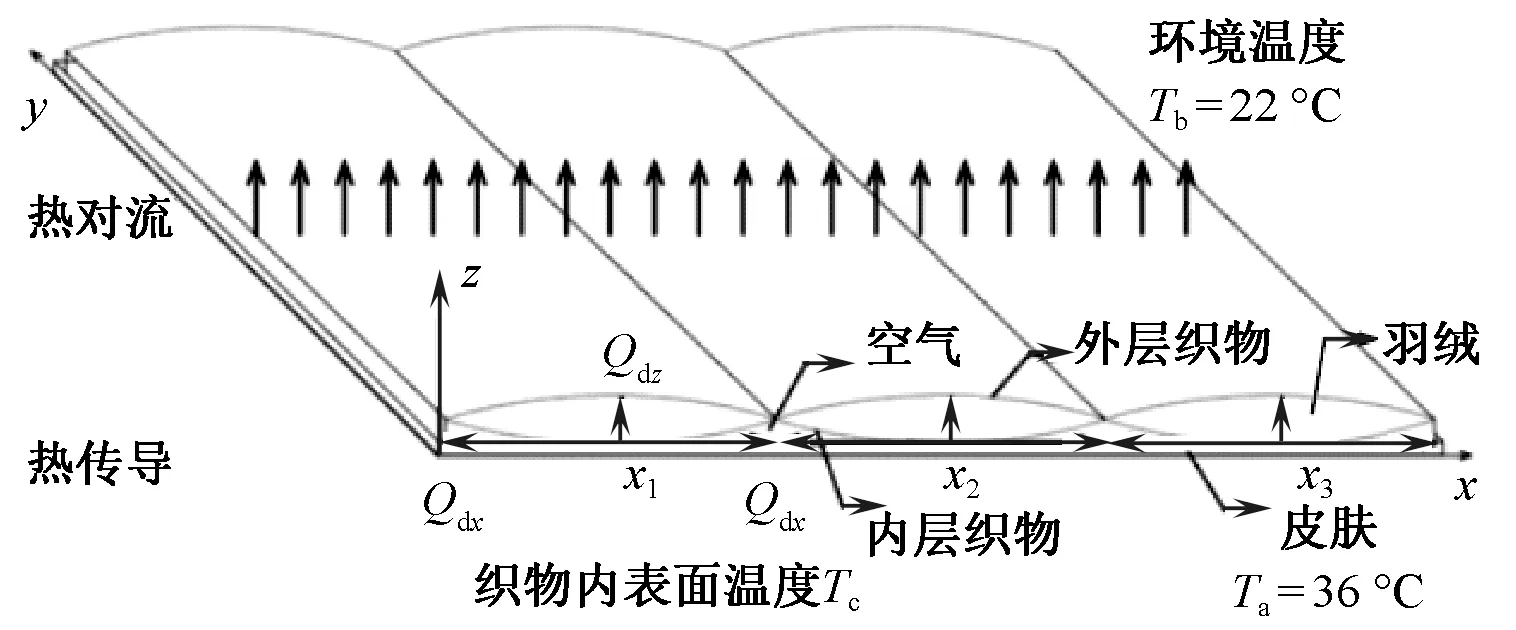
注：x轴表示模型宽度方向，y轴表示模型长度方向，z轴表示模型厚度方向；Qdx表示沿模型宽度方向热量，Qdz表示沿模型厚度方向热量；Ta表示织物外表面温度，Tb表示环境温度，Ts表示皮肤温度；x1、x2、x3表示皮肤热量作用在模型表面的位置。图1 稳态热传递三维过程图Fig.1 Steady state heat transfer process

1.2 热对流

以2条绗缝为例，绗缝后的“羽绒-织物-皮肤”几何模型，如图2(a)所示，横截面传热如图2(b)所示。

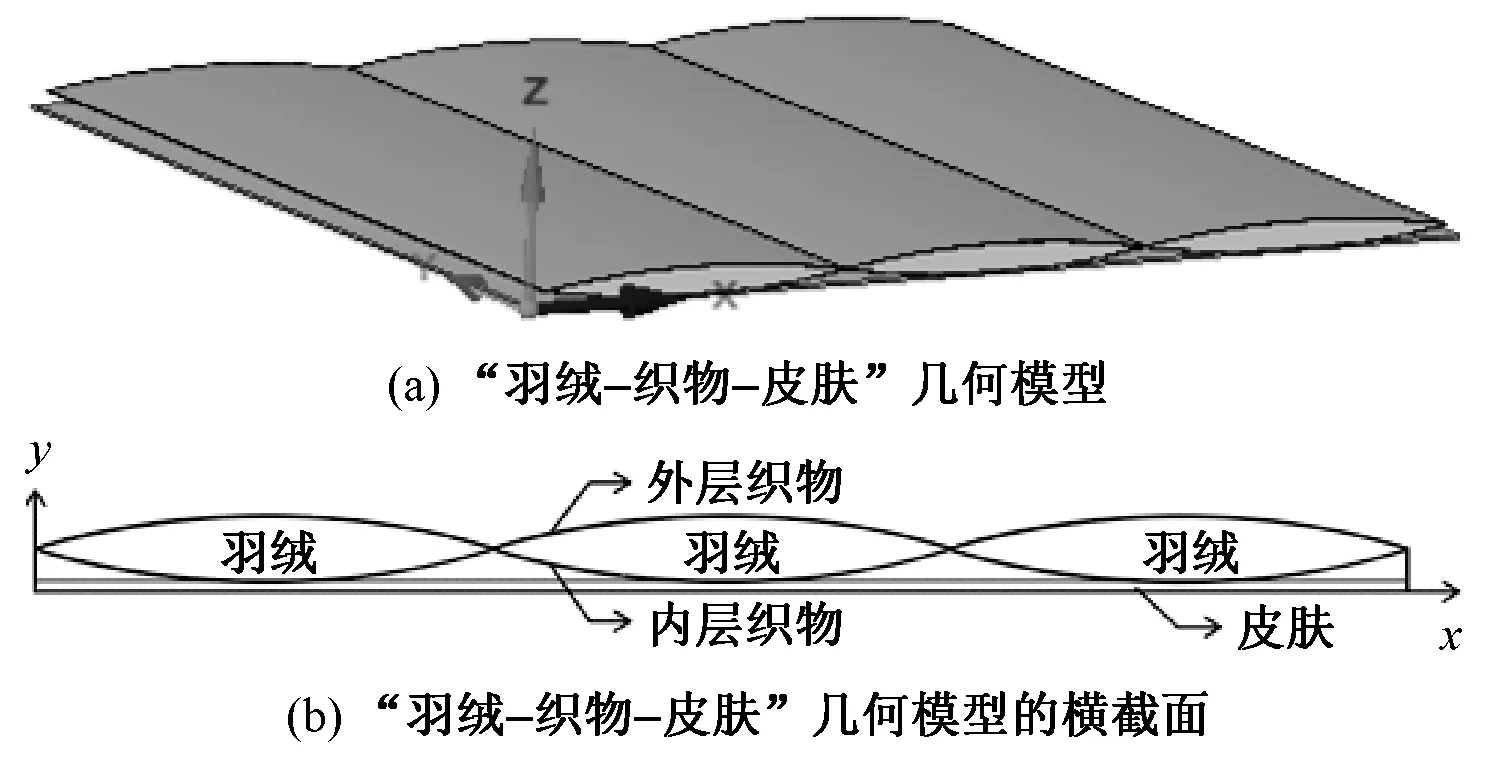
图2 绗缝后的“羽绒-织物-皮肤”简化模型Fig.2 Simplified model of "down-fabric-skin" tissue after quilting. (a) "Down-fabric-skin" combination; (b) Cross-section of "down-fabric-skin" combination

羽绒集合体在日常使用过程中，由于表面织物的包裹，外层空气难以进入，因此，可认为羽绒集合体内不存在强制对流，只有自然对流的发生。羽绒集合体可看作羽绒纤维与空气形成的多孔介质，集合体中的孔隙充满了空气。根据文献[13]可知，热对流不是羽绒集合体内热量散失的主要因素，可以忽略羽绒集合体内的热对流。因此，该模型仅考虑远离皮肤一侧织物表面的对流换热。

在皮肤、羽绒、织物与环境组成的系统中，远离皮肤一侧的织物表面以对流换热的方式传递给外界环境，可以用牛顿冷却公式来表示，即

q2=h(Ts-Tb)

式中：q2为热流密度，W/m2；h为对流换热系数，W/(m2·K)；Ts为织物外表面温度，℃；Tb为外界环境温度，℃。

1.3 热传导

绗缝后的羽绒实验袋内部各处的温度是均匀的，等于环境温度；在一侧给定恒定温度，等于皮肤温度，另一侧仍然与环境接触。此时，人体皮肤热量先传递至靠近皮肤一侧的织物，靠近皮肤一侧的织物温度很快上升，此时其他部分温度仍为环境温度，随着时间的推移，皮肤热量继续传递至羽绒中，最后传递到远离皮肤一侧的织物中，其他部分的温度逐渐升高，最终达到稳定。由图2可知，皮肤热量作用在绗缝后单个羽绒实验袋表面的中心位置处(x1，x2，x3)，单个羽绒实验袋内部温度呈对称分布，因此模型可以转化为(x，z)的二维。此时，热传导遵循傅里叶定律，可得羽绒实验袋内热传导方程：

式中：q3为热流密度，W/m2；λ为厚度方向导热系数，W/(m·K)；dt/dx表示沿模型宽度方向的温度变化率；dt/dz表示沿模型厚度方向的温度变化率，负号表示热量流向温度降低的方向。

根据热传导公式可知，不同织物导热系数不同，会导致羽绒实验袋导热系数改变从而影响热流密度；同样，不同填充密度的羽绒导热系数不同，也会导致羽绒实验袋导热系数改变从而影响热流密度。由图2可知，绗缝数量不同会导致皮肤热量作用在羽绒实验袋上的点的个数改变，影响宽度方向热量的传递，从而影响热流密度。

2 数值模拟

2.1 几何模型

本文选择织物、填充密度、绗缝数量3种羽绒保暖性影响因素作为模型的可变参数。选取4种常见的羽绒服织物：全弹春亚纺(100%涤纶)、尼丝纺(100%锦纶)、四面弹(90%锦纶，10%氨纶)、桃皮绒(100%涤纶)；4种羽绒填充密度为：60、80、100、120 g/m2；4种水平绗缝数量为：1、2、3、4条，参考羽绒实验袋试样尺寸制备方法，构建不同织物、填充密度及绗缝数量条件下“羽绒-织物-皮肤”的几何模型。组合方式如下：1)不同织物的几何模型中，织物选择全弹春亚纺、尼丝纺、四面弹、桃皮绒，填充密度为60 g/m2、绗缝数量为1条；2)不同填充密度、不同绗缝数量的几何模型中，织物选择全弹春亚纺，填充密度为60～120 g/m2，绗缝数量为1～4条。

制备羽绒实验袋试样：充绒前试样尺寸为30 cm×30 cm，选择含绒率为90%的羽绒，根据实验设置的填充密度，充进试样袋，再封充绒口。用手拍打试样，使其中的羽绒均匀分布后，再根据实验设置的绗缝数量采用水平绗缝的形式分别在试样上绗1、2、3、4条隔绒线，绗缝后的试样如图3所示。

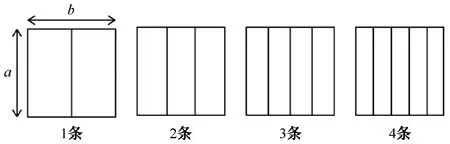
图3 不同绗缝数量的羽绒实验袋Fig.3 Down experimental bags with different quilting numbers

“羽绒-织物-皮肤”的几何模型如图4所示。x-z截面示意图如图5所示。通过测量可得，未绗缝一侧的试样宽度值，记为a(mm)，其中，由前期实验可知，未绗缝一侧宽度值对模型温度影响不大，因此设置其值保持不变，a=30 mm。充绒后，测量绗缝一侧的试样宽度值(包含织物厚度)，记为b(mm)。织物厚度通过YG(B)141D织物厚度仪测量，记为c(mm)。设置皮肤厚度为1 mm。

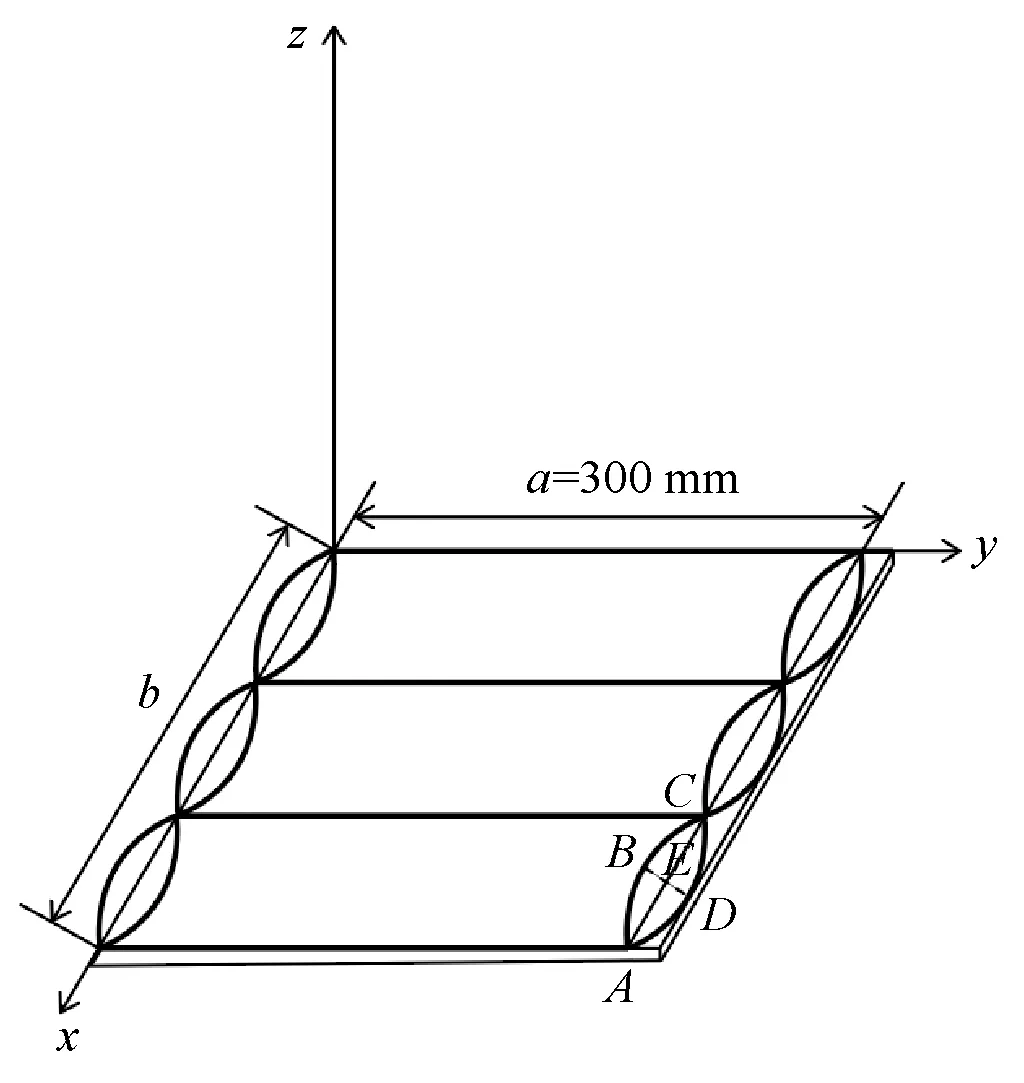
图4 “羽绒-织物-皮肤”几何模型图(以2条绗缝为例)Fig.4 Geometric model of down-fabric-skin(take 2 quilting lines as an example)

图5 几何模型截面示意图(以2条绗缝为例)Fig.5 Schematic diagram of cross-sectional geometry of an elliptic cylinder(take 2 quilting lines as an example)

由图4、5可知，水平绗缝试样体积可近似的视为若干个均匀椭圆柱体体积之和。图形ABCDA为一个截面，弧长AC可近似看作是圆上的一段弧线，圆心为O。B为弧AC中点，AC交OB于点E。当绗缝数量为n时，椭圆柱体数量为n+1。

式中：l为充绒前试样长度，mm；n为绗缝数量，条；b为绗缝后试样长度实测值，mm。

通过公式可求得半径r，根据试样b、r的值，建立不同织物、不同填充密度、不同绗缝数量的几何模型，图4中的几何模型可直接用于有限元模型的计算。由于不同织物绗缝后试样的宽度值差异不显著[14]，因此，为简化模型，测量4种织物模型的宽度值，求得其平均值为296 mm，将不同织物的几何模型的宽度值统一设置为296 mm。表1为填充密度为60 g/m2，绗缝数量为1条时，不同织物几何模型的试样数据。表2为织物取全弹春亚纺时，不同填充密度、不同绗缝数量几何模型的试样数据。

表1 试样数据Tab.1 Sample data

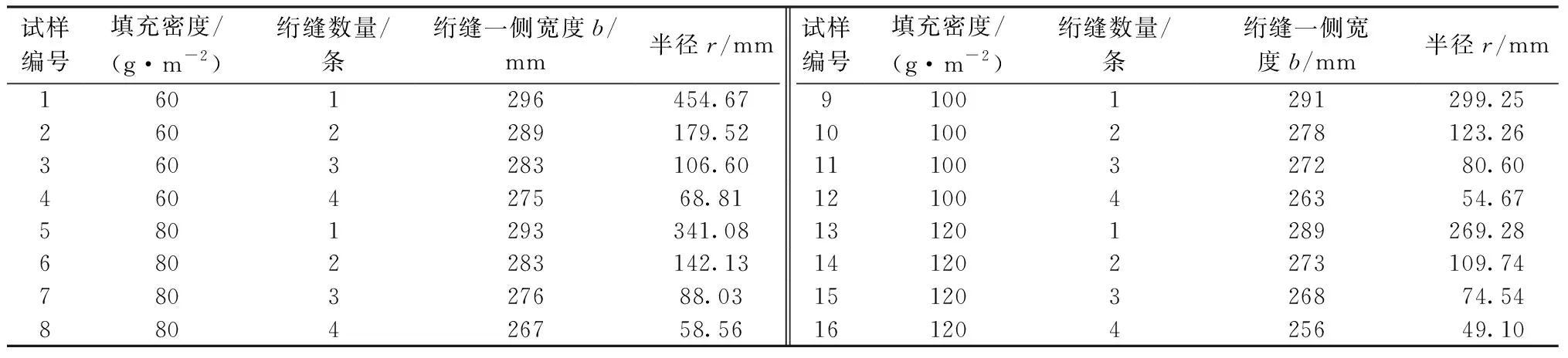
表2 试样数据Tab.2 Sample data

2.2 定义材料属性

根据所选的4种常见的羽绒服织物，分别设定全弹春亚纺、尼丝纺、四面弹、桃皮绒织物的材料参数，并赋予模型相应织物的材料属性。织物的相关参数如表3所示。

表3 织物参数Tab.3 Fabric parameters

羽绒的材料属性：为简化问题，将羽绒看作均匀的材料，不考虑羽绒纤维间的孔隙。根据所选4种填充密度的羽绒，将其放置于轻薄的非织造布袋中进行保暖性测试[15]，得到不同填充密度羽绒的导热系数：60 g/m2羽绒导热系数为0.044 1 W/(m·K)，80 g/m2羽绒导热系数为0.043 7 W/(m·K)，100 g/m2羽绒导热系数为0.043 2 W/(m·K)，120 g/m2羽绒导热系数为0.042 5 W/(m·K)，此处的导热系数是指沿非织造布袋z轴方向的导热系数，同时赋予模型相应填充密度羽绒的材料属性。

2.3 网格划分

在有限元模拟中，求解计算涉及的只有节点和单元，因此，几何模型创建完成后，需要对其进行网格划分，生成包含节点和单元的网格模型。网格划分的好坏将直接影响求解的准确性以及计算的速度。模拟采用自由网格划分方式，网格单元尺寸设置为0.01 m，图6示出填充密度为60 g/m2、绗缝数量为2条时羽绒实验袋划分后的局部网格模型，共有6 000个单元，42 998个节点。

图6 部分网格模型Fig.6 Part of the grid mode

2.4 施加载荷与边界条件

几何模型网格划分后，对其施加各种约束与载荷。本文采用稳态热传递进行模拟，羽绒实验袋一侧设定与人体皮肤相接触，设定温度为与YG(B)606D型平板式保温仪平板温度相同的36 ℃。羽绒实验袋周围环境温度参照YG(B)606D型平板式保温仪的测试环境温度，与实验环境保持一致，设置为22 ℃。织物和环境之间存在对流，对其施加对流载荷，自然对流时对流换热系数为10 W/(m2·K)[16]。

3 结果与分析

3.1 不同织物的热传递模拟

选择含绒率为90%，填充密度为60 g/m2，绗缝数量为1条时的羽绒实验袋模型进行稳态热分析，织物选择全弹春亚纺、尼丝纺、四面弹、桃皮绒4种常见的羽绒服面料，对其施加载荷求解。限于篇幅，以尼丝纺、四面弹织物为例，示出模型内部截面温度分布(见图7)。

图7 不同织物的羽绒实验袋温度分布图Fig.7 Temperature distribution diagram of down experimental bags of different fabrics.(a) Nylon spinning；(b) Four-sided bomb

由图7可知，人体皮肤的热量是沿着羽绒实验袋厚度方向以及宽度方向多维传递的，其中，厚度方向温度逐渐递减，宽度方向的温度呈中间高两边低分布。通过有限元模拟分析，可以得到羽绒实验袋远离皮肤一侧的表面平均温度。当传热平衡时，织物为全弹春亚纺、尼丝纺、四面弹、桃皮绒的模型表面平均温度分别为24.354、24.429、24.389、24.243 ℃。由于皮肤温度保持恒定，服装保暖性可由其表面温度表征，数值越低表明保暖性能越好[17]。不同织物的模型表面温度相差较小，说明不同导热率的织物对羽绒保暖性没有显著性影响。分析原因：由于不同织物模型的宽度值b相同，且织物的厚度在模型中远小于羽绒的厚度，织物的导热率对整体模型影响不大，因此织物对羽绒保暖性的影响不显著。

3.2 不同填充密度的热传递模拟

以含绒率为90%，绗缝数量为2条绗缝，织物选择全弹春亚纺的模型为例，对4种不同填充密度的模型进行稳态热分析，对其施加载荷与求解。以60、120 g/m2填充密度模型为例，示出模型内部截面温度分布(见图8)。

图8 不同填充密度的羽绒实验袋温度分布图Fig.8 Temperature distribution of down experimental bags with different filling densities.(a) Filling density is 60 g/m2；(b) Filling density is 120 g/m2

由图8可知，不同填充密度的几何模型中，羽绒实验袋的厚度随着填充密度的增大而增大，因此热量沿羽绒实验袋厚度方向传递距离也逐渐增大。当传热平衡时，填充密度为60、80、100、120 g/m2的羽绒实验袋表面平均温度分别为24.735、24.41、23.839、23.704 ℃。即不同填充密度的模型表面温度从大到小为60、80、100、120 g/m2。随着填充密度的增加，羽绒实验袋的表面温度逐渐降低。说明填充密度越大，羽绒保暖性能越好。

3.3 不同绗缝数量的热传递模拟

以含绒率为90%，填充密度为60 g/m2，织物选择全弹春亚纺的羽绒实验袋为例，对4种不同绗缝数量的模型进行稳态热分析，对其施加载荷与求解。以1、4条绗缝数量模型为例，示出模型内部截面温度分布(见图9)。

图9 不同绗缝数量的羽绒实验袋温度分布图Fig.9 Temperature distribution diagram of down experimental bags with different quilting numbers.(a) 1 quilting ；(b) 4 quilting

由图9可知，不同绗缝数量的几何模型中，随着绗缝数量的增加，模型厚度逐渐增大，模型宽度逐渐减小。皮肤热量沿着羽绒实验袋厚度方向的传递距离逐渐增大，沿宽度方向的传递距离逐渐减小。当传热平衡时，绗缝数量为1条绗缝、2条绗缝、3条绗缝、4条绗缝的羽绒实验袋表面平均温度分别为24.354、24.735、25.100、25.693 ℃，即不同绗缝数量的羽绒实验袋表面最高温度从大到小为4条绗缝、3条绗缝、2条绗缝、1条绗缝。随着绗缝数量的增加，羽绒实验袋的表面温度逐渐上升。说明绗缝数量越少，羽绒保暖性能越好。

3.4 绗缝数量、填充密度和热流密度的关系

对本文选取的不同填充密度、不同绗缝数量条件下的模型进行稳态热传递分析，对其施加载荷求解，载荷与边界条件如2.4节所示。得到传热平衡时模型的模拟热流密度值及相关参数，如表4～6所示。其中，以填充密度为60、120 g/m2，绗缝数量为1、4条，织物为全弹春亚的羽绒实验袋为例，模型内部截面热流密度分布云图如图10所示。

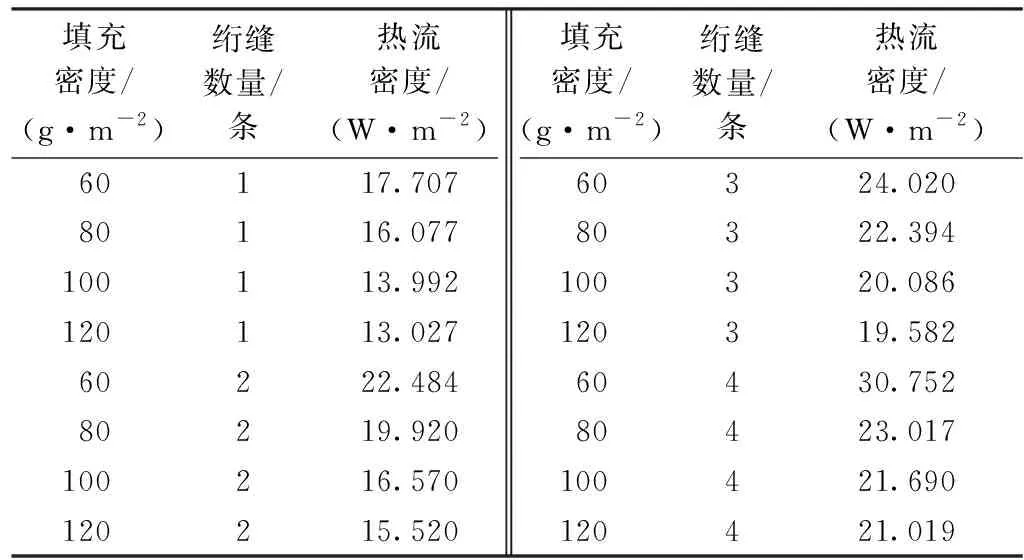
表4 模型模拟热流密度值Tab.4 Model simulation heat flux value

表5 热流密度的多元线性回归模型汇总Tab.5 Summary of multiple linear regression models of heat flux density

表6 热流密度回归系数表Tab.6 Heat flux regression coefficient table

由对比图10(a)、(b)可知，随着填充密度的增加，模型整体热流密度逐渐减小；由对比图9(a)、10(c)可知，随着绗缝数量的增加，热流密度逐渐增大。为了进一步探究绗缝数量、填充密度和热流密度的关系，根据表4数据，采用SPSS多元线性回归的方法对其进行拟合。

多元线性回归模型汇总如表5所示，调整后R2=0.904，接近于1，说明模型与数据的拟合程度较好。显著性水平小于0.05，说明线性关系明显。因此，可以得到拟合方程：y=-0.108x1+2.965x2+22.186。式中：x1为羽绒实验袋填充密度，g/m2；x2为羽绒实验袋绗缝数量，条；y为羽绒实验袋整体热流密度，W/m2。绗缝数量与热流密度呈正相关线性关系，填充密度与热流密度呈负相关线性关系。

4 实验验证

4.1 实验测试结果

为了验证模拟的有效性，制作填充密度为60 g/m2，绗缝数量为1条，织物为全弹春亚纺、尼丝纺、四面弹、桃皮绒的羽绒实验袋，共4个，为第1组试样；制作填充密度为60、80、100、120 g/m2，绗缝数量为1、2、3、4条、织物为全弹春亚纺的羽绒实验袋，共16个，为第2组试样。测试2组试样的保暖性能，实验在恒温恒湿实验室中进行，室内温度设定为22 ℃，相对湿度设定为(65±2)%，自然对流，实验设备为YG(B)606D型平板式保温性试验仪，将平板的温度设置为36 ℃。将试样平铺在实验板上，预热60 min，测定5个加热周期，每天开机做1次空白实验。每个样品测试3组数值，取平均值作为实验结果。

4.2 模拟结果

试样的保暖性由下式[18]计算：

式中：Tm为传热平衡时的试样靠近皮肤一侧的表面平均温度，℃；Tn为传热平衡时的试样远离皮肤一侧的表面平均温度，℃；q为模拟热流密度，W/m2。

根据ANSYS数值模拟结果，得到羽绒实验袋的内外表面温度差、热流密度，结合公式，计算羽绒实验袋的保暖性。将实验测试结果与模拟结果进行对比，结果见表7、8。

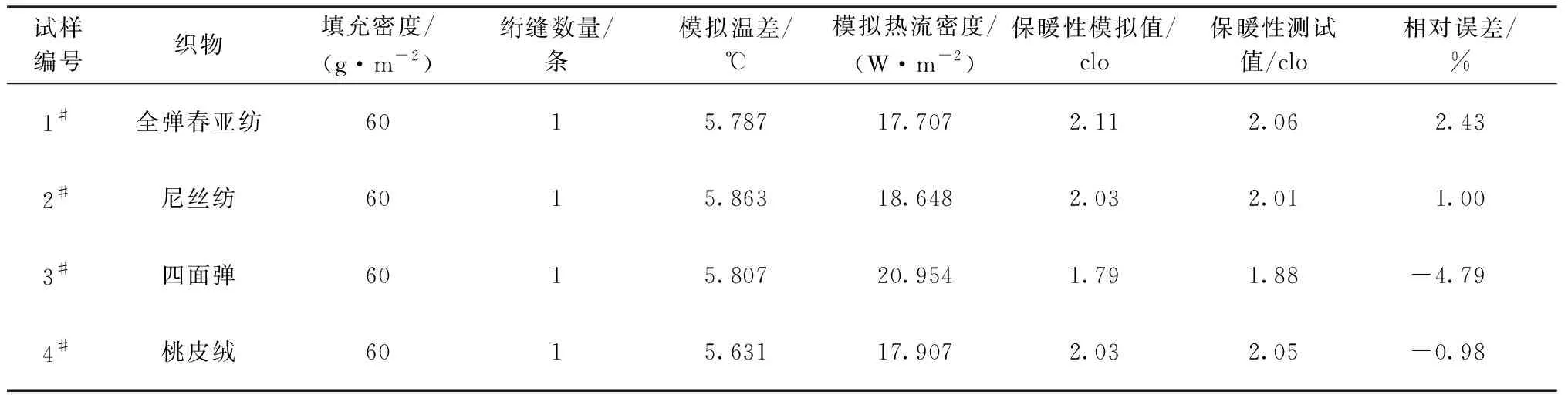
表7 有限元模拟结果与实验结果对比(第1组)Tab.7 Comparison of finite element simulation results and experimental results(the first group)

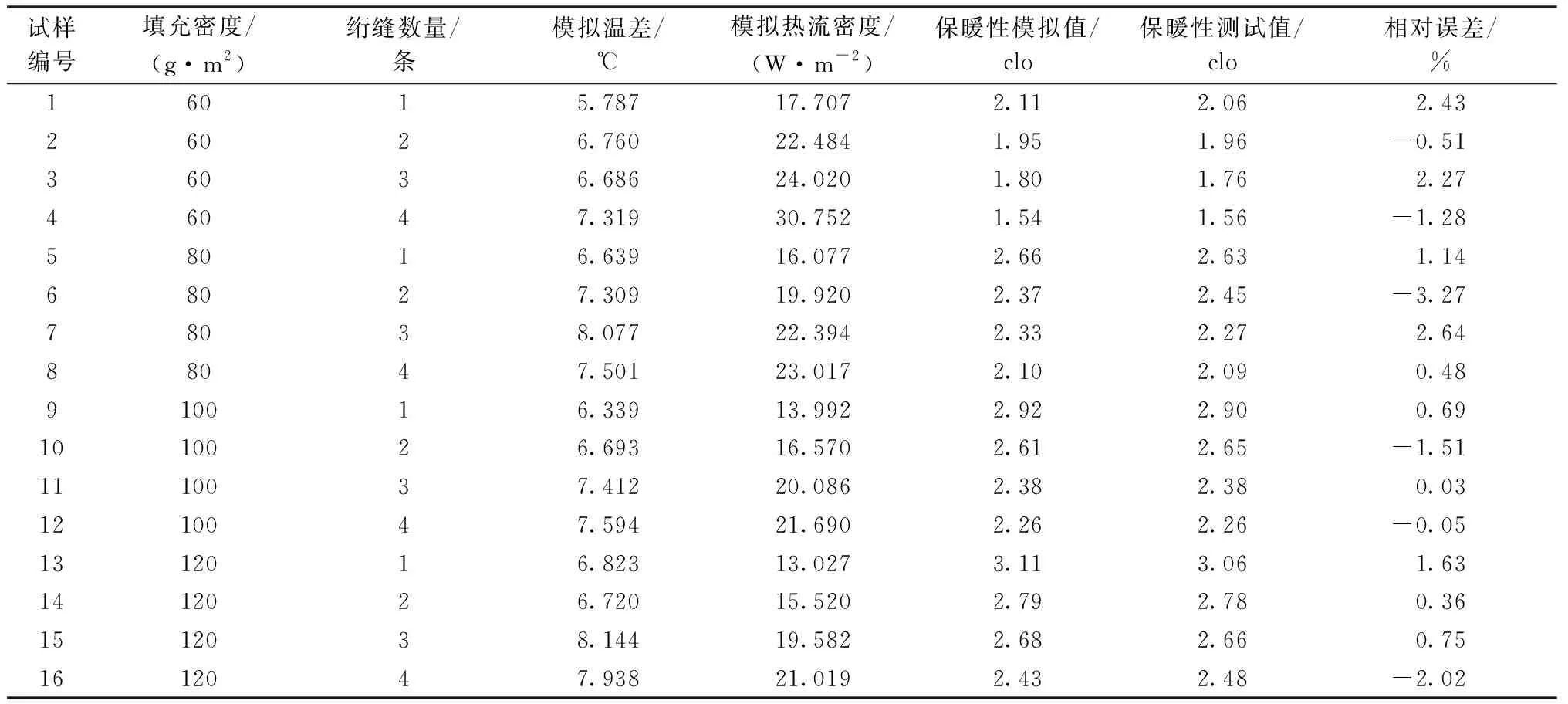
表8 有限元模拟结果与实验结果对比(第二组)Tab.8 Comparison of finite element simulation results and experimental results(the second group)

由表7、8可看出，不同织物、不同填充密度、不同绗缝数量的羽绒实验袋几何模型的有限元模拟结果与实验测试结果的最大相对误差为4.79%。说明羽绒实验袋模型的稳态热传递模拟结果与实际试验具有良好的吻合性。分析原因：第1组模型的误差是由于织物的弹性会影响羽绒实验袋模型的厚度，但本文不考虑织物对绗缝缩率的影响，因此会产生一定的误差；第2组模型的误差是由于实际羽绒纤维的结构很复杂，在扫描电子显微镜下，羽绒纤维截面近似椭圆形，内层呈现皮芯结构，芯层含有空洞甚至形成空腔，这就使羽绒纤维具有了轻盈、保暖的特性[19]。而本文没有根据羽绒的毛羽结构进行建模，因此理论数据与实验数据尚存在一定的误差，但存在的误差在可接受的范围内，证明有限元模拟的可行性。