砂砾石料颗粒级配参数的多维威布尔分布模型

裴彥青，李建锋，赵宇飞,刘 彪,李 锐

(1.新疆新华叶尔羌河流域水利水电开发有限公司，新疆 喀什 844000;2.中国水利水电科学研究院，北京 100048;)

1 研究背景

砂砾石料作为一种无黏性的粗粒土材料，具有较优的压实性能、填筑密度大、承载力高、抗剪强度高、沉陷变形小等诸多优良的工程特性[1- 4]。在中国地域辽阔的南疆地区，河床和戈壁沙漠中广泛分布着储量丰富的天然砂砾石，在当地水利水电开发中，砂砾石坝也因享有就地取材、结构简单、变形适应性好、施工工序少等工程优势而成为当地最常见的坝型之一[5]。在大坝填筑碾压过程中，掌握坝料的物理力学特性是有效控制土石坝填筑施工质量的关键，对坝体质量控制以及坝体安全稳定运行具有非常重要的意义。

在土石坝填筑施工过程中，不同粒径坝料按照一定的比例混合起来，通过不同的碾压工艺，使其达到符合要求的密实度，以满足上部结构对填方的要求，土石坝料的级配特征参数直接影响坝料填筑的压实特性；而坝体材料的渗透特性主要是由孔隙结构特征决定，级配是影响坝料孔隙结构特征的主要因素。因此，研究砂砾石料在一定压实度条件下的物理力学特性(压实特性和渗透特性等)，首先应对砂砾石料颗粒级配进行深入研究[6]。从国内外相关文献来看，不少学者通过室内试验或数值仿真等手段也开展了相关研究，均指出颗粒级配对砂砾石料的压实特性和渗透特性具有重要影响[7- 16]。如在级配表征压实特性方面，李晓柱等[11]依托糯扎渡现场试验情况，引入了离散元数值方法来研究堆石体的碾压特性，探讨了粒径分布对碾压质量的影响，并提出了最佳级配范围；朱晟等[12]结合室内试验和现场试验开展了堆石坝料级配特征对压实干密度的影响，并建立了具有分形分布的堆石料级配公式，证实了级配是影响堆石坝料压实性能的主要因素。在级配表征渗透特性方面，王双等[13]采用神经网络研究了碎石土级配对渗透系数的影响，研究发现P5含量(小于5mm的粒径)[11]、不均匀系数或曲率系数与渗透系数之间存在较强的相关性；张国栋等[14]通过室内试验研究了颗粒级配对渗透特性的影响，研究发现特征粒径、不均匀系数和曲率系数与渗透系数之间的关系符合线性拟合关系。

然而现有的相关研究基本上是基于室内试验或数值仿真等手段开展的研究，通过设计模型试验获取数据进行统计分析的方法，由于试验中数据量较少且未能考虑施工中的不确定性因素的影响，试验数据往往较为理想，所得方法用于拟合实际工程中的问题时通常难以较好地描述。此外相关研究仅考虑了砂砾石料颗粒级配中的某几个特征，未全面、细致考虑颗粒级配的变化，导致颗粒级配的代表性不足，虽然反映出颗粒级配对土的压实性和渗透特性存在影响，但是获得的相关影响规律尚不够深入[17]。当前试验方法仍然是确定其参数最直接、最可靠的方法，也是大多数理论和经验估值的重要依据[15]。充分利用有限的试验数据，结合概率统计方法探索颗粒级配与力学参数间的关系，是目前较为实用的途径。

根据已有的样本数据去推断总体分布时，一般需要将数据拟合成具体的概率分布模型，并估计其相应的分布参数，在数理统计分析中威布尔分析模型对各种类型试验数据有极强的适应能力，不仅能够适用于大样本数据，对小样本数据也有较好的适用性[18]，因此本文选用威布尔分布作为坝料级配特征参数的总体分布模型。在本研究中，依托新疆阿尔塔什水利枢纽工程施工过程中获取的大量检测试验数据，在大量统计的基础上，通过分析各参数与干密度和渗透系数之间的相关性，选取了与干密度和渗透系数相关性最密切的3个级配特征参数，并对其分别构建了一维威布尔分布模型，求出对应模型的3个控制参数：位置参数μ、尺度参数σ、形状参数ξ，得到了在一定保证率条件下的砂砾石料级配参数估计值。在此基础上，进一步推导出了三维威布尔分布函数表达式，建立了能够利用3个级配特征参数间相关关系反映砂砾石填料区干密度和渗透系数的三维威布尔分布模型，使干密度和渗透系数的表征方法更具综合性，可用于粗粒料的质量评估和预测。

2 多维威布尔分布模型的建立

2.1 一维威布尔分布模型的建立

在概率统计分析方面，威布尔分析模型能够较好的拟合数据样本点，适用于完全样本、有偏样本和截尾样本的拟合，对各种类型试验数据有极强的适应能力。三参数威布尔概率分布函数的表达式可表示为[19- 22]：

(1)

其密度函数为：

(2)

式中，F(x)—分布函数；f(x)—密度函数；x—随机变量；ξ—形状参数；σ—尺度参数；μ—位置参数。

威布尔分布参数求解常用的方法是最小二乘法[23- 25]，本文选用最小二乘法进行参数计算，初始计算时μ设定为任意小于样本数据最小值的数，进而可求出形状参数ξ和尺度参数σ：

(3)

此外在实际应用时，往往需要给出在一定可靠度条件下的参数估计值，设参数估计的可靠度为R2，则一维威布尔分布在可靠度R2条件下的估计值为[27]：

2.2 三维威布尔分布模型的建立

实际工程中坝料级配的描述，是一系列颗粒粒径及其含量的表达，这些参数在一定的尺度范围内存在着随机性和符合统计规律的自相似性，且某些参数间存在着明显的相关性[28]。因此，难以采用一维概率分布进行全面描述，但目前多维概率分布中参数、相关系数确定以及假设检验仍存在困难，限制了多维概率分布在坝料级配特性表达中的应用。

近年来不少研究者逐步完善了多维复合极值分布理论[29- 31]，本研究受上述离散型多维复合极值分布模型建立思想的启发[32- 35]，在一维威布尔分布的基础上，构建了基于威布尔分布的多维复合分布函数模型。对于三维威布尔分布而言，其概率分布函数应该是每个变量的边缘函数的组合，考虑三维威布尔概率分布中变量之间的相关系数，通过公式推导与数值拟合，得出的三维威布尔分布模型概率函数的数学表达式为：

(5)

式中，ξj、μj、σj—x，y，z的边缘分布形状参数、位置参数和尺度参数，j=1，2，3；0≤α，β≤1为由相关系数r得到的相关参数，α，β均为1时，x，y，z相互独立。史道济[36]通过矩估计法，给出了相关参数α，β的显式表达式：

(6)

2.3 拟合优度检验

在评估上述所获得的概率分布模型的拟合精度，本文采用了K-S检验(Kolmogorov-Smirnov)来检验指定的威布尔分布和实际分布是否相符，具体检验步骤如下[37]：

(1)建立原假设H0:G(x)=F(x)，其中F(x)为假设的分布函数，G(x)为样本观测值得累积分布函数：G(xi)=i/n，i=1，2，…，n。

(2)计算检验统计量：Dn=max{|Fn(x)-F(x)|}。

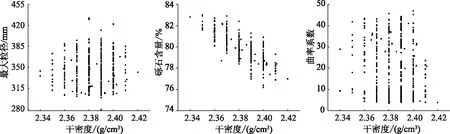
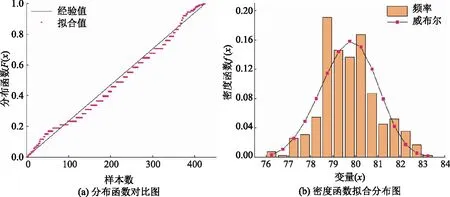
(3)在不同显著性水平α下，比较Dn与K-S检验临界值表中的临界值D(n，α)。若Dn

3 工程应用

3.1 工程背景

阿尔塔什水利枢纽工程位于塔里木河源流之一的叶尔羌河干流山区下游河段的新疆维吾尔自治区克孜勒苏柯尔克孜自治州阿克陶县库斯拉甫乡境内，是一座在保证向塔里木河干流生态供水目标的前提下，承担防洪、灌溉、发电等综合利用任务的大型骨干水利枢纽工程。水库工程正常蓄水位为1820.0m，水库设计洪水位为1821.62m，校核洪水位为1823.69m，总库容22.49亿m3；电站装机容量755MW。阿尔塔什水利枢纽工程为大(1)型一等工程。

阿尔塔什水库混凝土面板砂砾石堆石坝坝体横剖面图如图1所示，坝轴线全长795.0m，坝顶高程1825.80m，坝顶宽度为12m，最大坝高164.8m，上游坝坡采用1∶1.7，下游坝坡坡度为1∶1.6。面板坝直接建造于河床深厚覆盖层上，覆盖层最大厚度94m。大坝抗震设计烈度为9度，100年超越概率2%的设计地震动峰值加速度为320.6g。坝体填筑分区从上游至下游分别为上游盖重区、上游铺盖区、混凝土面板、垫层料区、过渡料区、砂砾料区、利用料区、爆破料区。

图1 阿尔塔什混凝土面板堆石坝坝体横剖面图

3.2 影响坝料物理力学特性的级配参数确定

筑坝砂砾填料的物理力学特性(压实特性和渗透特性)具有级配相关性，但在砂砾石料施工质量控制中，目前主要以含砾量表征级配对物理力学特性的影响，未考虑级配形状、最大粒径、不均匀系数、曲率系数的影响。已有研究表明，砂砾石料压实特性和渗透特性受这些因素的影响较为显著，而简化的室内实验确定的级配参数难以准确描述现场原级配料的干密度和渗透系数。在此基础上推导出来的外延公式缺乏普遍适用性，应用时存在较大的误差。为了研究这些参数对其敏感性，本研究借助数理统计的方法，基于施工过程中大量的检测试验数据，建立试验参数间的关系，选择与干密度和渗透系数相关性最紧密的3个因素，并对这3个因素通过威布尔分布进行拟合分析，推导出在一定保证率条件下的估计值。

在阿尔塔什水利枢纽工程堆石坝工程施工过程中，本文收集整理了堆石坝工程检测资料中砂砾石料挖坑质量检测试验数据504组和渗透试验数据45组，每组试验中的数据包含：干密度(g/cm3)、渗透系数(cm/s)、砾石含量(%)、含泥量(<0.075mm/%)、曲率系数Cc、不均匀系数Cu和最大粒径(mm)。由于大坝填筑实际施工过程中实时采集到的数据受卫星点位、地形地貌等的影响，不可避免的会产生一定的异常值，需要将这些异常值从数据集中剔除。本研究采用箱形图的四分位区间检测异常值的方法，该方法从实际样本数据出发，不限制数据服从某种特定的分布形式，可以比较简明直观的反映数据真实的面貌，在异常值识别处理方面具有一定的优越性。针对异常值数据本文采用剔除的方式处理，计算所得的干密度和渗透系数与其他级配特征参数的相关性r见表1，由表可知，与干密度相关性最密切的三个特征参数为：最大粒径、砾石含量、曲率系数；与渗透系数相关性最密切的3个特征参数为：含泥量、砾石含量、曲率系数。这3个因素与干密度的相关性关系如图2所示，限于篇幅，仅列出砂砾填筑料颗粒级配参数与干密度之间的关系。

图2 砂砾石料颗粒级配特征参数相关散点图

表1 砂砾石料物理力学特性相关性分析

3.3 基于一维威布尔分布的砂砾石级配参数拟合

根据第2.1节推导的威布尔分布拟合公式，编制相应的程序对与干密度和渗透系数最为相关的级配特征参数逐个进行拟合，进而计算出威布尔分布的3个参数，构建一维威布尔概率分布模型。分别对各参数的实际有效数据进行一维威布尔分布拟合，限于篇幅，此处仅列出与干密度最为相关的级配特征参数的拟合结果如图3—5所示，对应的威布尔分布参数见表2—3，从拟合结果可以看出，威布尔分布拟合结果的相关系数r均超过0.98，拟合结果较为可观。然后利用K-S检验法分别对本文威布尔分布拟合得到的概率分布进行检验，K-S检验法结果见表2—3所示，从表中可看出在在显著性水平α=0.01条件下，威布尔分布拟合得到的各项级配参数的概率密度函数都通过了拟合良好性检验，能够真实反映随机变量的概率分布情况。说明本研究的威布尔分布模型能够较好的适用于坝体填料试验数据的描述及参数估计，具有较好的应用前景。

图3 最大粒径～维威布尔分布拟合

图4 砾石含量～维威布尔分布拟合

图5 曲率系数～维威布尔分布拟合

表2 表征压实特性的级配威布尔分布模型参数

表3 表征渗透特性的级配威布尔分布模型参数

3.4 基于三维威布尔分布的砂砾石级配参数拟合

通过对干密度和渗透系数主要影响因素的相关性分析，得出了在砂砾石填料区与干密度和渗透系数各自相关性最密切的3个因素，但这3个参数间还同时存在着相关性。基于此，将这3个参数利用推导出的公式(5)建立三维威布尔分布模型。其中，此时的频率分布不再是一维威布尔分布中的单个参数的频率，而是同时满足3个参数时的频率。计算结果如图5所示，图中横坐标表示三维变量分组的个数，纵坐标表示分布函数值，图6(a)是砂砾石填料区基于最大粒径、砾石含量、曲率系数间相关关系建立的三维威布尔分布模型，用于表征坝料的压实特性；图6(b)砂砾石填料区基于含泥量、砾石含量、曲率系数间相关关系建立的三维威布尔分布模型，用于表征坝料的渗透特性。由图可知，三维威布尔分布较好地拟合了试验结果，能够同时考虑3个参数对坝料物理力学特性参数的影响，使坝料物理力学特性参数的表征方法更具综合性。

图6 三维威布尔分布拟合

4 结语

本文通过系统的概率理论推导研究，并结合阿尔塔什水利枢纽真实坝料筛分试验结果，进行了砂砾石坝填料多维概率分布拟合研究与应用探讨。在构建一维威布尔分布模型基础上，进一步推导出了三维威布尔分布函数表达式，建立了能够利用颗粒最大粒径、砾石含量、曲率系数间的相关关系反映砂砾石填料区压实特性的三维威布尔分布模型，以及利用含泥量、砾石含量、曲率系数间相关关系反映砂砾石填料区渗透特性的三维威布尔分布模型，使坝料的干密度和渗透系数的表征方法更具综合性，可用于砂砾填料的质量和变形的评估和预测。