电能表计量性能评价及预测方法研究

李铭凯,李 蕊,史鹏博,李雪城,程诗尧,丁 宁

(国网北京市电力公司电力科学研究院，北京 100162)

0 引言

随着供电企业智能电能表的大规模安装，以及基于IR46标准的新型电能表的规模化推广应用[1]，表计检定和供应量不断增加。目前，国家电网公司各省级计量中心为提高检定效率和规范性，大范围引入智能检定与仓储设备。同时，为实现电能表的及时分拣、充分利用、规范处置，供电企业均已开展电能表拆回分拣检测。其中，具备条件的企业已开展智能分拣与仓储系统的自动化分拣检测[2-3]。当前，电能表检测仅以基本的合格和不合格作为判定标准，对分拣合格的电能表缺乏进一步评判。因此，实施电能表计量性能评价及预测，对拆回分拣合格的电能表重新投运及在线监控具有重要意义。

电能表数量庞大，难以将其逐个拆开以测量不同器件和参数对其计量性能的影响。因此，本文利用电能表的检测数据对其进行研究分析[4]。

目前，利用检测数据对电能表进行评估已有一些相关研究[5-6]。文献[7]将层次分析法(analytic hierarchy process,AHP)引入电能表计量性能评价决策过程,提出了一种基于AHP的全面分析电能表计量性能的理论方法，以更好地判断电能表计量性能情况。文献[8]～文献[10]探究利用聚类方法对电能表进行评价，以实现电能表选型。但上述文献研究只利用首次检定数据，未计及不同时间维度对电能表的影响；同时，主要利用误差原始值维度，未考虑不同特征维度对评价结果的影响。

基于以上问题，本文提出了一种基于K-means聚类算法对电能表进行计量性能评价，并利用电能表基本信息特征对其评价类别进行预测的方法。该研究主要创新工作为：①考虑不同时间维度对电能表计量性能评价的影响，由于表计数量庞大，不同表计首次检定和拆回检测时间差异大，需综合考虑计及多时间尺度的影响；②考虑多特征维度对计量性能评价的影响，构建均值、方差、平均偏移量、最大偏移量误差等多特征维度，对表计进行分析；③提出利用K-means聚类算法对电能表计量性能进行评价，进而以Stacking模型对其进行预测，并采用合成少数类过采样技术(synthetic minority oversampling technique,SMOTE)提升模型预测准确率。预测结果验证了模型的有效性。

1 电能表计量性能评价方法

电能表作为电能计量器具，其基本误差反映其计量性能。本文针对电能表拆回检测及其首次检定的基本误差情况，对其计量性能进行评价。

1.1 评价方法研究

利用电能表基本误差数据对电能表进行计量性能评价的原则是计量性能与误差特征值成反比。其本质上是针对误差特征数据分布情况进行评价。

本文利用拆回检测和首次检定不同时间维度的误差数据对电能计量性能进行分类评价。误差数据在特征空间的分布情况代表其计量性能的差异。但对误差数据进行分析存在以下两点问题。

①电能表误差数据为数值型数据，具备连续性特点，分布较为密集。如果人为划分计量性能评价分界线主观性强，难以合理进行。

②检定数据中只有电能表合格与不合格之分，没有针对误差数据作进一步细分，所以表计没有计量性能评价分类标签数据。

针对以上两个问题，需对比常用的分类评价算法。分类算法对比如表1所示。

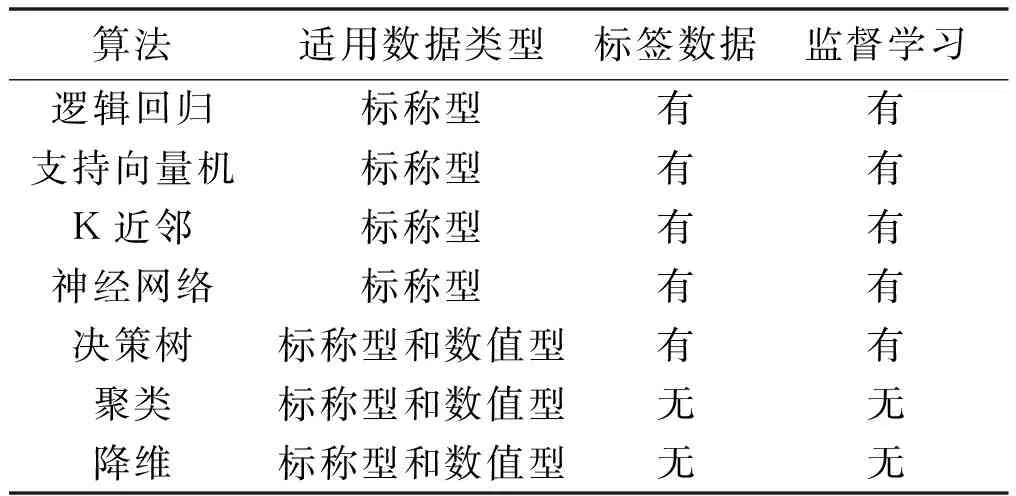
表1 分类算法对比

由表1可知，监督学习各算法需要标签数据进行分类评价，不适用于电能表数据集。无监督学习算法中，聚类和降维算法既可以处理连续数值型数据，又不需要标签数据。但是降维算法一般用作压缩数据。而聚类算法可根据数据分布自动分类，因此适用于电能表数据集分类评价。本文采用经典的K-means聚类算法对电能表进行计量性能评价。

1.2 K-means算法

1.2.1 K-means算法步骤

K-means算法步骤如下。

①从数据中选择k个对象作为初始聚类中心。

②计算每个聚类对象到聚类中心k的距离。

③针对每个类别，重新计算聚类中心。

④重复步骤②和步骤③，直至聚类中心位置不再发生变化。

1.2.2 K-means算法流程

K-means具体计算流程如下。

输入为样本集A={x1,x2,...,xm}、聚类的簇树k、最大迭代次数N。输出为簇划分C={C1,C2,...Ck}。

(1)从数据集A中随机选择k个样本作为初始的k个质心向量：μ={μ1,μ2,...,μk}。

(2)对于样本集A={x1,x2,...,xm}，计算如下。

①将簇划分C初始化为Ct=φ，t=1,2,...,k。

④如果所有的k个质心向量都没有发生变化，则转到步骤(3)。

(3)输出簇划分C={C1,C2,...,Ck}。

簇个数k的选择对K-means算法非常重要，而轮廓系数法可用于选择最优k值。该方法可评估聚类效果。轮廓系数计算如式(1)所示。

(1)

式中：S为轮廓系数；ai为样本点i与同一簇中所有其他点的平均距离，即簇内相似度；bi为样本点i与下一个最近簇中所有点的平均距离，即簇间相似度；D为样本点的个数。

K-means追求的是对于每个簇而言，其簇内差异小而簇外差异大。轮廓系数S正是描述簇内外差异的关键指标。由式(1)可知，S的取值范围为(-1,1)。当S越接近1，聚类效果越好；越接近-1，聚类效果越差。

1.3 误差特征构建

特征构建利用电能表不同时间维度的误差数据进行。由于每只电能表误差数据正负并存，而零误差点为理想误差点，直接利用原始误差数据分析数据点分散时波动性强，难以直观表征其计量性能分布情况。因此，为了对每只电能表进行计量性能评价，需要根据基本误差数据构建特征量。

根据误差测试数据，可直接以均值与方差表征每只电能表误差分布情况。同时，为了进一步分析误差分布情况，并与理想的零误差点相关联，本文定义平均偏移量和最大偏移量两个变量。

平均偏移量即所有误差测试点距零点的平均距离。

(2)

式中：P为平均偏移量；xi为误差值；M为样本点的个数。

最大偏移量即所有误差测试点距零点的最大距离。

Z=max{|xi|,i=1,2,...,M}

(3)

式中：Z为最大偏移量。

本文构建了均值、方差、平均偏移量、最大偏移量四个特征量。这四个特征分别代表了电能表四个不同维度的分布情况。因此，本文利用K-means算法分别对这几个特征维度进行计量性能评价，并选出最合适的评价维度。同时，每只电能表有首次检定和拆回检测两个时间维度的特征数据，记为[x1,x2]。

1.4 实例应用

本文数据集为省级计量中心调度平台系统的20 549只电能表的首次检定和拆回检测的检测数据，检定数据来源于基本误差、起动试验等测试项目。基本误差测试点如表2所示。

表2 误差测试点

针对构建的特征数据集，首先计算轮廓系数以确定最佳分类数k。均值、方差、平均偏移量、最大偏移量四个维度的轮廓系数随k值变化曲线如图1所示。

由图1可知，均值、方差、平均偏移量和最大偏移量四个维度轮廓系数最大时k均为2。根据轮廓系数性质可知，将本文利用的电能表误差特征数据分为两类效果更好。同时，k=2时平均偏移量维度的轮廓系数最接近于1，表明以平均偏移量维度进行聚类评价效果最好。经分析，这种结果主要与误差数据分布情况和四个维度特征计算方式相关。误差越接近零点，代表电能表计量性能越好。均值计算存在正负相抵现象，即使均值为0也可能每个测试点误差与零点距离较大。方差则为计算与表计误差均值的离散程度而非误差零点。最大偏移量是绝对值计算，不存在均值和方差的问题。但若测试点误差分布极不平衡，最大偏移量也无法代表表计整体的计量性能。平均偏移量计算同样不存在均值和方差的问题，并兼顾所有测试点的误差分布情况，因此更适合评价电能表的计量性能。

因此，本文最终选取平均偏移量维度，采用K-means算法将构建的电能表误差特征数据分为两类。聚类结果如表3所示。

表3 聚类结果

对于聚类而言，每个类别中心点代表该类别的整体性质和分布。分类后的类别1中心点数值为类别2的倍数级，而误差特征值越小则计量性能越好。因此，类别2电能表优于类别1。

同时，该结果表明聚类评价后类别1和类别2的数据个数差别较大，聚类后的数据集类别不平衡。

2 电能表计量性能预测方法

2.1 预测方法研究

本文数据集中，除了误差数据还包括电能表基本信息，如生产厂家、到货批次、运行单位、运行供电所、运行时间等。这些基本信息代表不同电能表的差异。

计量性能预测方法如图2所示。

本文以运行天数、到货批次和运行供电所为例进行分析。运行天数代表时间因素，运行越久则电能表元器件越老化，越影响计量性能。到货批次代表生产因素。表计同一到货批次为厂家连续时间内生产，设备生产情况相同，因而能代表生产因素对表计计量性能的影响。运行供电所代表地理位置因素。不同地理位置由于温湿度等环境因素不同，对表计计量性能的影响也不同。

考虑到上述因素与计量性能相关，同时前文已经利用K-means聚类算法对计量性能进行分类评价，因此本文提出利用电能表基本信息特征对其评价类别进行预测。

机器学习中可用于分类和预测的算法较多，比如支持向量机 (support vector machine,SVM)、决策树算法 (decision tree classifier,DTC)、K近邻(K-nearest neighbors,KNN)等。同时，为了提升模型效果，集成学习也在相关任务中广泛应用。本文提出利用Stacking集成学习模型进行预测。

预测具体步骤如下。

①以电能表基本信息构建特征数据集，以K-means聚类评价的结果构建标签集。

②针对数据集类别不平衡进行处理。

③将处理后的数据集输入Stacking模型进行训练及预测。

2.2 Stacking模型原理

Stacking模型框架整体分为两层。首先，将原始数据集以交叉验证方式划分成若干子数据集，输入第一层的各基学习器中。每个基学习器输出各自的预测结果。然后，将第一层的输出作为第二层元学习器的输入值，对元学习器进行训练，再由元学习器输出最终预测结果。Stacking 模型通过结合多个模型的优点，提升整体预测效果。 Stacking模型框架如图3所示。

①假设第一层共有n个基学习器，则对于每个基学习器进行步骤②和步骤③的训练。

②将数据集划分为训练集U和测试集V，并将训练集分为f份。每次选出训练集中的(f-1)份进行训练，剩余 1 份进行测试。预测后，输出结果ui(i=1,2,...,f)，并以该学习器对测试集进行训练，输出预测结果vi(i=1,2,...,f)。

③将f个ui纵向拼接成为新的训练集U′ ,f个vi相加求平均成为新的测试集T′。

2.3 基学习器及元学习器

考虑到机器学习不同模型的差异，综合利用不同模型的优势，本文选取了单模型算法SVM、KNN和集成学习模型梯度提升决策树(gradient boosting decision tree,GBDT)、极端梯度提升(extreme gradient boosting,XGBoost)作为Stacking的基学习器。

SVM分类算法是在特征空间中寻找间隔最大化的分离超平面的线性分类器，通过引入核函数实现非线性分类。SVM可以解决小样本情况下的机器学习问题和高维问题，但它对大规模训练样本难以实施、对缺失数据敏感、对参数和核函数的选择敏感。

KNN分类算法在分类决策上只依据最邻近的一个或者几个样本类别来决定待分类样本所属的类别。KNN简单、易于理解、无参数估计、不需要进行训练，但当样本分布不均匀时容易判别错误，对高维数据效果不佳。

集成学习是将多个弱分类器构成一个强分类器，一般能够提升分类器的性能。其中之一的GBDT以损失函数的负梯度作为当前决策树的残差近似值，去拟合新的决策树，是一种串行训练方式。GBDT适用于分类和回归问题，可灵活处理各种类型的数据，对异常值的鲁棒性非常强。但GBDT算法中弱学习器之间存在依赖关系，难以并行训练数据。同时，在每一次迭代时，都需要遍历整个训练数据多次。由于内存限制，GBDT算法不适合处理大规模数据。

XGBoost是GBDT算法的高效工程实现。相比GBDT，XGBoost加入正则项来控制模型的复杂度，在特征选择上利用列抽样方式，有利于防止过拟合。XGBoost对损失函数进行二阶泰勒展开，可同时使用一阶和二阶导数，并支持多种类型的基分类器。它在树分裂过程中的特征选择可并行训练，提升了运行效率。

考虑到集成学习方法效果较好和XGBoost的工程优势，本文选取XGBoost作为第二层训练的元学习器。

2.4 分类不平衡处理

K-means聚类算法对电能表进行分类评价后，两个类别的比例为5.5∶1。学习器对类别数量差别较大的数据集容易造成学习偏置问题，即将所有样本预测为多数的类别。

针对此问题，本文采用过采样方式将少数类别数据进行扩充成多数类别的数量。由于采取简单复制样本的策略来增加少数类样本，容易产生模型过拟合的问题，因此本文采用SMOTE算法合成少数类的样本。算法具体步骤如下。

①假设少数样本集为B。对于少数类中每一个样本b，以欧氏距离为标准计算它到少数类样本集中所有样本的距离，得到其l近邻。

②根据样本不平衡比例设置一个采样比例以确定采样倍率P。对于每一个少数类样本b，从其l近邻中随机选择若干个样本，假设选择的近邻为e。

③对于每一个随机选出的近邻e，按式(4)构建新的样本。

bnew=b+rand(0,1)×(b-e)

(4)

式中：bnew为新样本；b和e分别为样本和其近邻；rand为随机函数。

2.5 特征构建

电能表基本信息统计如表4所示。

表4 电能表基本信息统计表

由表4可知，所有电能表基本电流、基本电压、准确度等级均一致，无法体现差异，因此对计量性能预测并无作用，需将其删除。其余基本信息有差异，同时均为离散值，可将其作为电能表的特征进行类别编码，如运行年数含6个值分别编码为0、1、2、3、4、5。将基本信息特征进行类别特征编码后，可将其作为特征集，并将计量性能评价类别作为标签集，对数据集进行训练及预测。

2.6 实例应用

将本文原数据集划分为训练集和测试集，利用Stacking模型训练，并与各基学习器单独训练对比。不同模型预测准确率如表5所示。

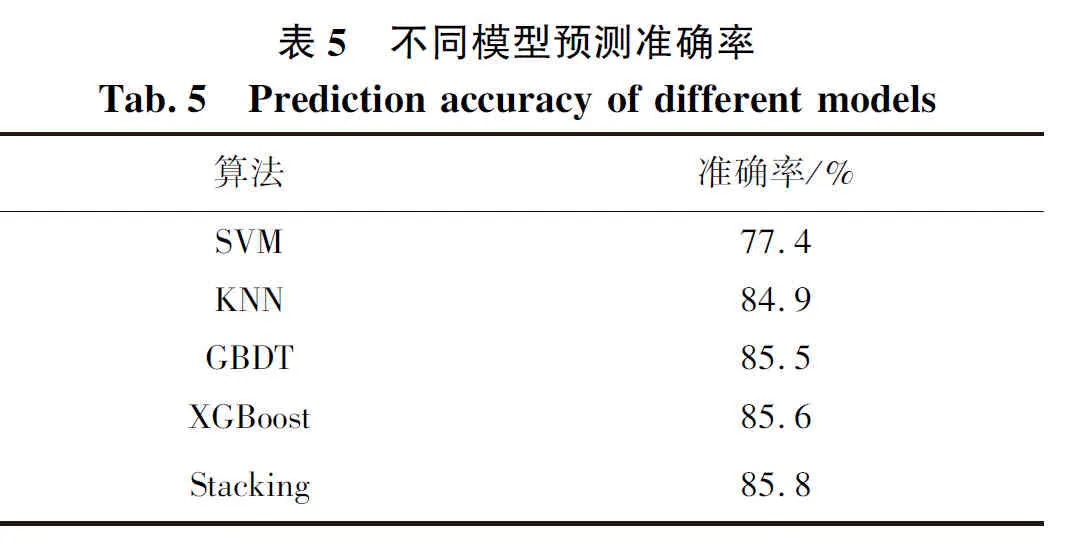
由表5可知，本文提出的Stacking模型准确率最高，达到85.8%，表明本文提出的Stacking模型有效。

对原数据集用SMOTE过采样后，进行训练及预测。过采样后的不同模型预测准确率如表6所示。

表6 过采样后的不同模型预测准确率

由表6可知，经过SMOTE采样后，虽然KNN算法的准确率略降低，但SVM、GBDT、XGBoost和Stacking模型的准确率均有不同程度的提高，平均提升2.75%。这表明本文利用SMOTE算法处理类别不平衡数据是有效的。而且本文提出的Stacking模型准确率最高达到88.5%，进一步证明Stacking模型的有效性。同时，较高的准确率也证明了本文提出的利用电能表基本信息特征对电能表计量性能预测方法的有效性。

3 结论

本文提出了一种电能表计量性能评价及预测方法。首先，计及时间因素和不同误差特征维度对电能表计量性能评价的影响，利用电能表拆回检测及其首检数据，提出利用K-means聚类算法对电能表计量性能进行评价。均值、方差、平均偏移量、最大偏移量四个维度的研究分析结果表明，平均偏移量效果最好，更适合对电能表进行计量性能评价。可根据评价结果对计量性能相对较差的电能表进行更加全面的检测，对拆回分拣后重新投运的电能表进行不同级别的监控，同时可进一步挖掘不同生产厂家计量性能评价结果分布，为选择厂家提供技术参考。然后，本文在计量性能评价的基础上，进一步提出一种利用电能表基本信息特征预测其计量性能评价类别的方法。采用集成学习Stacking模型进行预测，以SVM、KNN、GBDT和XGBoost相异模型为Stacking模型基分类器，并利用SMOTE处理数据集类别不平衡问题。预测结果证明了Stacking模型和SMOTE的有效性。同时，较高的预测准确率验证了本文所提方法的有效性。所提预测方法可用于分析拆回分拣后重新投运和在运的电能表。在不考虑突发情况等不可控因素的前提下，该方法可不获取在运电能表运行数据而利用其基本信息对其计量性能作出较为准确的预测。预测结果可作为电能表离线计量性能判断依据，对在运电能表进行选择性监控。