计及碳减排的配电网扩展规划模型与方法研究

包忠强，于 明，郭 华，林 信，关卓钰

(1．广西电网有限责任公司，广西 南宁 530023；2．太原理工大学电气与动力工程学院，山西 太原 030024)

0 引言

近年来，加速能源清洁低碳转型已成为全球性议题。2020年9月，我国提出了“碳达峰”“碳中和”的重大战略目标[1]。能源的生产、输送和消费活动是CO2的主要排放源，而电力部门又是主要的碳排放部门。因此，在电力系统的规划和运行等各环节实现低碳转型是达成双碳目标的关键。

在低碳的配电网规划研究领域，研究人员已开展了较多的研究工作。文献[2]～文献[4]研究了低碳要素引入对传统电源规划的影响。文献[5]、文献[6]指出，与传统的规划模式相比，“电源-网架”协调规划模式具有更好的低碳特性，更有利于低碳能源的发展。文献[7]对不同碳减排技术展开研究，针对碳捕集系统与风电协调规划问题，给出符合经济要求的投资规划方案。现有文献侧重于分析碳排放因素对电源规划的影响，而在考虑碳排放因素的网架扩展规划方面的研究还较少。

本文通过在规划目标中引入碳排放量因子来量化配电网运行所产生的碳排放量，并将新建配电变压器、新建配电馈线与新建分布式风电机组作为待选方案，进而提出了1种新的计及碳减排的多目标配电网扩展规划模型。为了降低模型求解的复杂度，本文针对该模型所包含的非线性表达式提出了相应的线性化处理方法，将该模型转化为混合整数线性规划模型，从而对规划模型进行高效的求解。

1 配电网扩展规划模型

1.1 目标函数

本文所提出的计及碳减排的配电网扩展规划模型包含配电网规划成本和总的碳排放量2个目标。目标函数F可以表示为：

F=min{FTC,FEm}

(1)

式中：FTC为配电网规划成本；FEm为总的碳排放量。

1.1.1 配电网规划成本

FTC包含2部分，即运行成本和投资成本。运行成本包括从主网购买电能的成本，并且假设风电机组的运行成本为零。投资成本包括新建配电馈线、配电变压器和风电机组的成本。

(2)

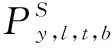
(3)

式中：B′为配电馈线的数量；Cb′为新建配电馈线每公里的建设成本；lb′为新建配电馈线的长度；γy,b′,f为第b′条配电馈线所对应的投资决策变量，为二进制变量。

(4)

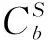
在规划周期的每个阶段，对于第b′条配电馈线而言，其可能需要强化建设，也可能不需要强化建设。γy,b′,f=1=1意味着第b′条配电馈线在第y年需要强化建设。而γy,b′,f=2=1意味着第b′条配电馈线在第y年不需要强化建设。同理，ψy,b,tr有着类似的定义。

新建风电机组的投资成本为：

(5)

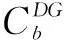
基于以上分析，有：

(6)

1.1.2 总的碳排放量

配电网所产生的总CO2排放量的计算式为：

(7)

式中：Em为配电网的碳排放量因子，表示每兆瓦时发电量所产生的CO2量，t CO2/MWh。

配电网中的碳排放量均由发电时化石燃料燃烧产生。国际上大多数国家的燃煤电厂平均每发一度电需要消耗的煤炭通常为320 g标准煤。

碳排放量计算式为：

(8)

由式(8)可知，配电网的碳排放量因子Em为0.87。

1.1.3 目标函数

由于本文所提出的配电网扩展规划模型是1个多目标最优化模型，因此可以采用帕累托前沿方法[8]求得最终的目标函数表达式。本文采用权重系数法来求解帕累托最优集合，则式(1)可以表示为：

Fmin=ω1×FTC+ω2×FEm

(9)

式中：ω1、ω2为权重系数。

通过改变权重系数(ω1、ω2)，可以求解得到最优的帕累托集合。

1.2 约束条件

1.2.1 网络潮流约束

网络潮流约束计算式为：

(10)

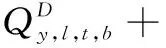
(11)

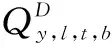
(12)

(13)

1.2.2 热容量极限约束

热容量极限约束为：

(14)

(15)

1.2.3 配电变电站潮流方向约束

配电变电站潮流方向约束为：

(16)

1.2.4 电压幅值约束

电压幅值约束为：

(17)

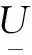
1.2.5 功率因数约束

功率因数约束为：

(18)

式中：φ为节点b处配电变电站的功角。

1.2.6 风电机组运行约束

风电机组运行约束为：

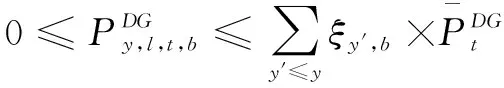
(19)

1.2.7 逻辑约束

逻辑约束为：

(20)

(21)

2 模型求解方法

本文所提出的计及碳减排的配电网扩展规划模型是1个混合整数非线性规划(mixed integer non-linear programming,MINLP)模型。其非线性表达式为式(13)和式(15)，其余均为线性表达式。

式(13)与式(15)所包含的非线性项可以分成2类，即某2个变量的乘积项和某个变量的平方项。本文针对这2类非线性项提出相应的处理方法，使其能够线性化表示，从而大大降低模型求解的复杂度。

(22)

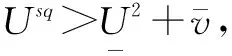
xs≤xs-1,xs∈{0,1}

(23)

其次，通过利用离散化变量首区间的中点，可以将非线性项作线性化表示：

(24)

(25)

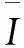
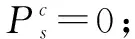
(26)

对于非线性项(PF)2，本文采用平方变量分段线性化的方法对其进行线性化处理。该非线性项可以表示为：

(27)

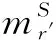
P+-P-=PF

(28)

式中：P+和P-为所引入的2个辅助正变量，用于求得PF的幅值和符号；PF的幅值等于离散化后的各个分段值之和。

(29)

(30)

0≤P+,P-

(31)

式(31)给出了每个分段值的上限。

基于以上分析，利用式(22)～式(31)，即可对本文所提出模型中的式(13)和式(15)这2个非线性表达式进行线性化表示。

在采用本文所提出的线性化方法进行处理之后，本文所提出的计及碳减排的配电网扩展规划模型被转化为1个混合整数线性规划(mixed integer linear programming,MILP)模型，从而可以采用现有的成熟软件——通用代数建模系统(general algebraic modeling system,GAMS)[9]对该简化后的规划模型进行有效求解。

3 算例分析

配电系统接线如图1所示。

本文以文献[10]所给出的配电系统为例，验证本文所提出的计及碳减排的配电网扩展规划模型的有效性。图1所示的配电系统包含1个配电变电站(节点1，其容量为40 MVA)，以及8个负荷节点。

40 MVA变电站接线如图2所示。

每个负荷节点的基本负荷如表1所示。基本电价为：居民用电108美元/MWh；工商业用电91美元/MWh。文献[10]所提配电系统的规划周期为5年。每个负荷节点的负荷增长数据见文献[10]。

表1 基本负荷

为文献[10]所提配电系统制订扩展规划方案时，待选的具体方案措施包括：新建2台容量为10 MVA的配电变压器，建设成本为20万美元/台；新建若干条配电馈线，建设成本为15万美元/km；新建若干台容量为0.5 MVA的风电机组，建设成本为122.7万美元/MVA。

每小时的负荷水平系数与电价水平系数如图3所示。

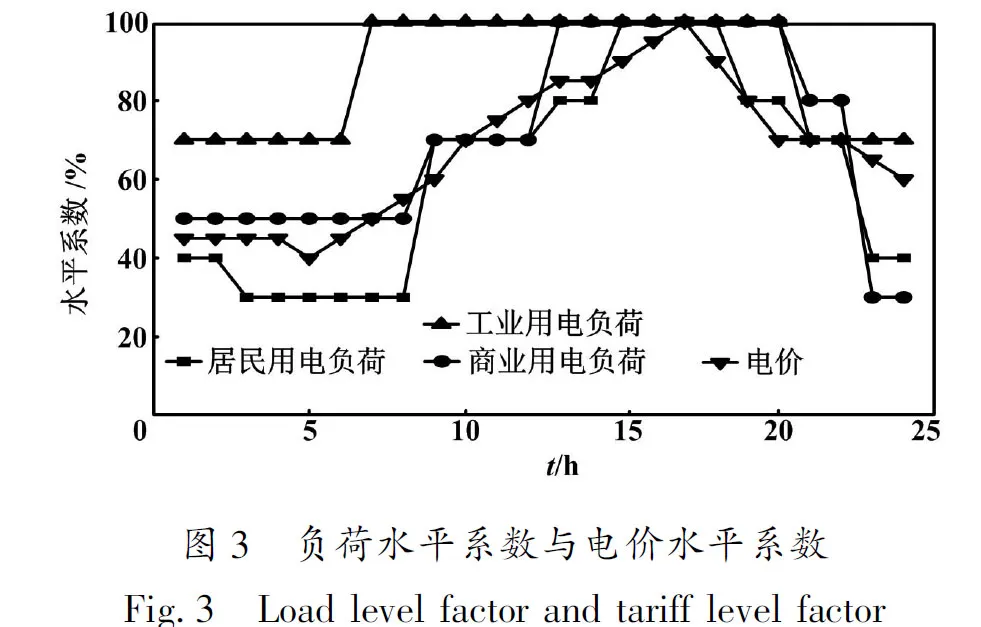
由图3可知，电价水平系数在居民用电、商业用电、工业用电负荷水平达峰值一段时间后最高，而后马上下降。因此，电价水平系数受居民和商业用电负荷水平影响较大。

假设折现率为12.5%、配电变电站的功率因数为0.85，并且在文献[10]所提配电系统的任意1个负荷节点上都可以新建风电机组。

本文给出2个算例，分别分析碳减排因素对配电网扩展规划的影响。在算例1中，FTC与FEm的权重系数是相等的，即认为总的碳排放量与配电网规划成本具有同等的重要性。在算例2中，令FEm的权重系数为零，即只把配电网规划成本作为目标。

3.1 算例1

为了评估风电机组对配电网扩展规划的影响，以下分别讨论2种方案。方案一是将新建配电变压器和新建配电馈线作为配电网扩展规划的待选方案措施。方案二是将新建配电变压器、新建配电馈线和新建风电机组均作为待选方案措施。

2种方案所得到的配电网扩展规划结果如表2所示。

表2 配电网扩展规划结果

新建风电机组的位置和容量为：第1年1.5 MW(6)、1.5 MW(8)、0.5 MW(9)；第2年1 MW(5)、0.5 MW(6)；第3年0.5 MW(3)、0.5 MW(8)；第4年0.5 MW(8)、0.5 MW(9)。

由表2可知，方案二既能够降低配电网规划成本，又能够减少配电网总的碳排放量；同时，新建风电机组对配电网规划成本的降低程度(32%)要远大于对配电网总碳排放量的减少程度(1.3%)。

在规划周期结束后，2种方案所得到的配电网扩展规划结果如图4所示。

由图4可知，方案二的新建风电机组能够延缓一些配电馈线的建设，从而起到降低配电网规划成本的作用。其主要原因在于新建设的风电机组距离负荷中心较近。这同时减少了配电馈线上的电流大小，起到了降低网络损耗的作用。

此外，图4表明，几乎所有的风电机组都被建设在远离配电变电站的负荷节点上，从而最大程度地减少了总的网络损耗。

3.2 算例2

与算例1相同，按照是否把新建风电机组作为待选的方案措施，算例2同样有2种方案。在算例2中，方案二能够使得配电网规划成本降低13%。

仅计及规划成本的配电网扩展规划结果如表3所示。

表3 仅计及规划成本的配电网扩展规划结果

新建风电机组的位置和容量为：第1年1.5 MW(6)、0.5 MW(8)；第2年0.5 MW(2)。

由于在算例2中没有计及总的碳排放量这一目标，2种方案所得到的配电网扩展规划结果的总碳排放量都比算例1中相应地有所增多。然而，就算例2本身来说，方案二仍然比方案一的总碳排放量降低了23%。

在规划周期结束后，仅计及规划成本的配电网扩展规划结果如图5所示。

由图5可知，算例2在方案一比算例1在方案一所需要新建设的配电馈线的数量有了明显的减少。这是因为在算例2中仅计及经济性目标而没有计及环境目标。

4 结论

本文通过引入碳排放量因子来计算配电网运行所产生的碳排放量，提出了1种计及碳减排的多目标配电网扩展规划模型。该模型新建配电变压器、新建配电馈线与新建分布式风电机组均作为待选的方案措施，使得经济性目标和环境目标同时达到最优。为了降低模型求解的复杂度，本文针对该模型所包含的非线性表达式提出了相应的线性化处理方法，将该模型转化为1个混合整数线性规划模型，从而能够采用现有的成熟软件——GAMS对该模型进行有效地求解。以某配电系统为例，通过分析和讨论不同情况下本文所提出模型的规划结果，验证了该模型的有效性。

算例分析中将新建风电机组加入备选方案措施，在极大地降低配电网规划成本的前提下(算例1为32%，算例2为13%)，配电网总碳排放量都相较之前降低了(算例1降低1.3%，算例2降低23%)。这表明，将新建风电机组作为待选方案不仅能够得到更具经济性的网络结构，而且能够有效降低配电网总的碳排放量。

需要指出的是，通过将环境目标替换为其他类型的目标(例如可靠性目标等)，本文所提出的多目标配电网扩展规划模型与方法将会在国家双碳战略目标下，具有更加广泛的适用性。