基于LSTM-CA模型的土地利用动态模拟
2022-12-23刘春霖夏建新
刘春霖, 夏建新
(中央民族大学生命与环境科学学院,北京 100081)
0 引言
随着城市化进程的快速发展,人类对土地资源大力开发利用,导致区域范围内地表覆被时空格局发生巨大变化,不但改变了城市地表景观结构,而且影响陆地生态系统的物质循环、能量流动及其稳定性。因此,为了实现区域生态环境的科学保护,必须对城市土地变化规律有充分的认识和研究。
近年来元胞自动机模型(cellular automata, CA)在时空动态模拟领域受到广泛关注,CA提供了时空动态模拟运算框架,利用自下而上的模拟方式,由局部规则演化出全局的变化模式,实现了受宏观地理条件和土地利用局部变化双重作用下的土地利用变化模拟[1-7]。Von Neumann[8]首次将CA定义为一个离散的动力学模型,由个体之间局部的行为演化出时间与空间上全局的变化模式。CA模型可与统计学方法和人工智能方法结合,实现更加精确、智能的复合模型。土地利用覆被变化过程是一个复杂的非线性变化过程,有学者指出需要建立转换规则自动获取方法应对复杂的土地利用变化过程。他们对利用统计学理论自动提取元胞转换规则的研究取得了突破性进展,例如多层感知机(multi-layer perceptron, MLP)、支持向量机 (support vector machine, SVM)和随机森林(random forest, RF)模型[9-10]。
随着深度学习的不断发展,越来越多的深度学习模型被应用于土地利用分类及变化模拟中,卷积神经网络是深度学习中常用的一种网络模型,它通常使用卷积滤波器来提取局部区域的隐含特征。He等[11]考虑到空间效应,利用卷积神经网络提取驱动因素的空间特征来模拟土地利用变化。然而这些方法都是在一定假设理论基础上进行的,即某个单元的状态只与上一个时间步骤的状态有关,与其他时刻状态无关[9,12-14],但是土地利用变化是一个长期过程,因此这些模型对于历史土地利用变化规则并未得到充分挖掘。
在深度学习模型中递归神经网络用于建立时间序列数据之间的依赖性,它可以在时间步长之间传递历史信息,但普通的循环神经网络(recurrent neural network, RNN)在实际应用中很难处理长距离的依赖。长短时记忆网络(long short term memory network, LSTM)成功解决了原始RNN的问题,能够对具有长时间依赖性的时间序列进行建模,能够充分考虑历史时序土地分类的时间变化特征,被广泛应用于土地覆盖分类中[15-16]。因此,本文以张家口市中心城区(包括桥东区、桥西区及万全区)为研究对象,将1995年、2000年、2005年、2010年、2015年历史土地利用数据作为基础数据,提出将LSTM和CA模型结合来模拟2020年土地利用的动态变化,最后将模拟结果与实际2020年土地利用分布结果比较,证明本文提出的LSTM-CA模型能够有效提高土地利用变化模拟准确性。
1 研究区概况及数据处理
近年来随着城市化的不断发展,张家口市中心城区(桥东区、桥西区及万全区)面积迅速扩张,该区域土地类型变化明显,因此本文以张家口市中心城区为主要研究区,如图1所示,该区域位于N40.645°~41.059°,E114.440°~114.996°之间,其中桥东区及桥西区以清水河为界,研究区域主要是山地与河谷地,其海拔范围为800~1 500 m。

图1 研究区概况图(Landsat8 B7(R),B5(G),B2(B)合成遥感影像)Fig.1 Overview of the study area
本文以1995年、2000年、2005年、2010年、2015年、2020年Landsat5/8遥感数据为基础,参考《城市用地分类与规划建设用地标准》,通过卷积神经网络将研究区划分为耕地、建设用地、水体、林地、草地5类土地利用类型,根据研究实测调研数据进行精度检验,总体分类精度达90%以上。
土地利用变化的概率往往取决于一系列的距离变量和单元的自然属性等。例如,某一模拟单元越接近市中心及交通要道,其转变为城市用地的概率越高。由于研究区所在区域主要是山地与河谷地,土地利用分布受地形影响显著,因此河流水系是影响该城市土地分布的主要因素之一。与此同时,随着城市化的不断发展,其土地利用变化与城市交通紧密相连,土地利用变化受人类活动影响显著,对于地势相对平缓的区域,人类活动相对频繁,城市交通分布更加复杂,因此,本文在选择驱动因子时主要考虑城市水系、地形及交通等指标,其中地形因素包括高程、坡度、坡向等信息,对于交通因素主要选取市中心点、高速公路、火车站、城市主干道、城镇点、村庄点等要素,越是靠近城市中心,交通分布就越复杂,因此,利用ArcGIS软件距离分析工具,计算研究区内每一点到城市交通要素的最近欧式距离,以此作为土地利用变化另一空间指标,并对这些空间变量进行归一化处理,结果如图2所示。除此以外,邻近现有土地利用类型的数量对于土地利用变化也有一定的影响,例如当邻近范围内存在同一种土地类型越多,该单元在下一时刻不变的概率就较高,在本文中将与当前土地利用单元状态相同的邻域单元数量加入空间变量中。

(a) 高程 (b) 坡向 (c) 坡度 (d) 到城市中心距离 (e) 到高速公路入口距离

(f) 到火车站距离 (g) 到主干道距离 (h) 到城镇距离 (i) 到村庄距离 (j) 到河流水系距离图2 地形、距离变量空间分布Fig.2 Spatial distribution of terrain and distance variables
2 研究方法
将LSTM网络、CA和地理信息系统(geographic information system,GIS)相结合进行土地利用动态模拟,流程如图3所示,图中x1,x2,…,xT表示时间序列的输入样本数据,h1,h2,…,hT表示时间序列的输出特征。主要流程包括: ①基础数据获取,包括计算各历史时期初始化的土地分类概率,统计相同土地利用状态的邻域单元数量,生成驱动因子; ②根据基础数据在研究区内随机生成训练样本数据; ③基于长时间序列土地分类数据,利用LSTM网络开展土地利用发展概率计算; ④通过添加扰动因子、限制因子和邻域因子进行土地利用全局转化概率计算,开展土地利用动态模拟研究。
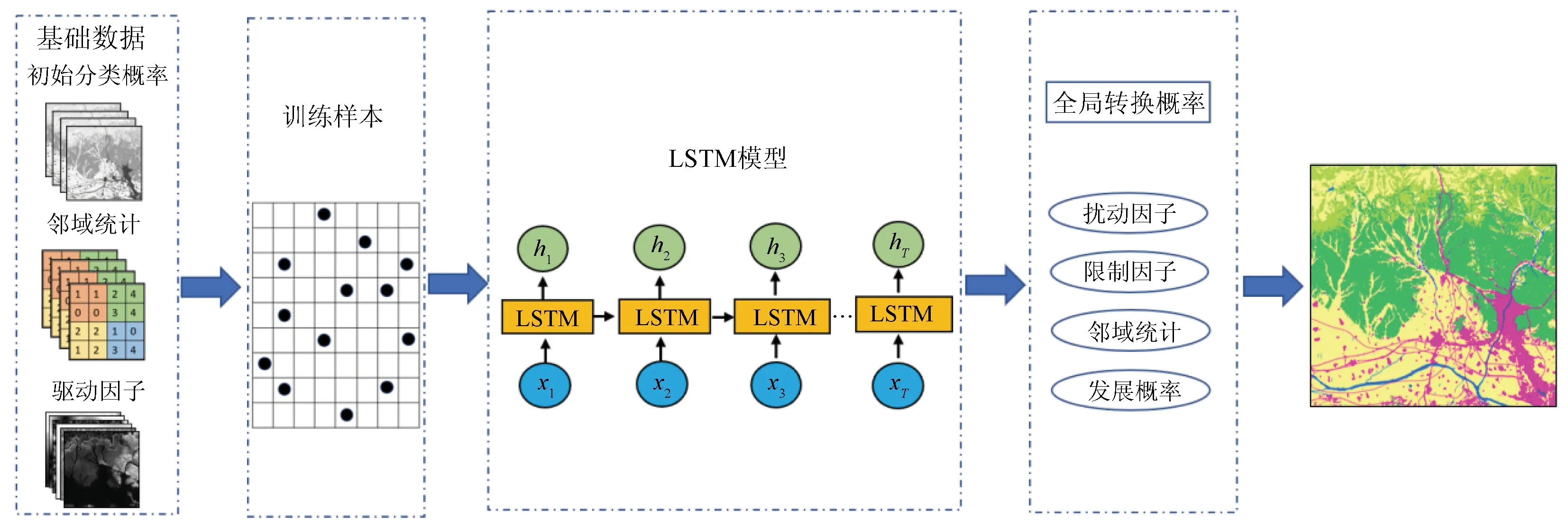
图3 LSTM-CA流程Fig.3 Process of LSTM-CA
2.1 基于LSTM网络的土地利用发展概率计算
LSTM(图4)作为一种特殊RNN,可以解决长时间序列数据在训练中的梯度爆炸和消失问题。对于普通的RNN,权重在各个时间上是共享的,由于梯度被近时间梯度主导,导致模型难以学到远距离的依赖关系。对于LSTM网络,由于总的远距离梯度等于各条路径的远距离梯度之和,因此,LSTM能够在更长时间序列数据中具有更好的表现。RNN通常由一系列循环单元组成,相对于普通RNN,LSTM在循环单元的基础上增加了门限限制,这样可以使得信息进行有效过滤,在LSTM中每一个单元都有输入门、输出门和遗忘门3部分组成,其结构如图4所示。图中σ为sigmoid激活函数;tanh为tanh激活函数; 红色线表示遗忘门; 绿色线表示输入门; 蓝色线表示输出门;xt为当前时刻输入数据;ht表示当前时刻的特征输出; ⊕和⊗分别表示加操作和乘操作。
遗忘门限控制当前单元状态中丢弃的信息,利用当前时间的输入和前一个时间的输出来通过sigmoid函数来使得单元状态乘以这个sigmoid函数的输出。若sigmoid函数输出0则该部分信息需要被丢弃或遗忘,反之该部分信息继续在单元状态中继续传播。输入门限层是控制更新旧的单元状态。之前的遗忘门限中sigmoid 层决定哪些信息需要更新,通过 tanh 激活函数计算用来更新的内容,把这2部分联合起来,对单元状态进行更新。输出门限是对单元状态的限制,从而决定输出的信息。假设X=(x1,x2,…,xt,…,xT)表示时间序列的输入,H=(h1,h2,…,ht,…,hT)表示经过LSTM后对应时间序列的输出特征,则X与H之间的映射关系可以表示为:
(1)
(2)
(3)
(4)
(5)
(6)
式中:it为t时刻输入门限;σ为sigmoid激活函数;W为全连接网络的权重;b为全连接网络的偏置;Ct为t时刻单元状态;ft为t时刻遗忘门限;ot为t时刻输出门限。
在本文中,LSTM采用了历史土地利用分类及驱动因子作为输入向量,xt=[xt1,xt2,…,xt16],其中xt1~xt5表示t时刻土地利用分类概率,xt6表示t时刻与当前土地利用单元状态相同的邻域单元数量,xt7~xt16分别表示高程、坡向、坡度、到市中心距离、到城镇距离、到村庄距离、到高速公路入口距离、到火车站距离及到主干道距离等驱动因子。在模型训练阶段,将1995—2010年4期土地利用分类及驱动因子作为LSTM模型的输入,通过实际2015年土地利用构建交叉熵损失,采用Adam算法优化网络模型。在预测阶段,采用2000—2015年4期土地利用及驱动因子数据作为输入,模拟2020年土地利用单元发展概率。
2.2 基于LSTM-CA模型的土地利用模拟
LSTM计算的发展概率只考虑各种空间变量对土地转化的影响,在CA中邻域元胞状态对土地转化同样至关重要,例如邻域元胞有较多转变为建设用地,则该元胞转化为建设用地的概率也越大。因此,本文选择3×3邻域窗口计算土地类型所占的比例作为邻域因子Ω,公式为:
(7)
式中:si为第i个元胞3×3邻域中单元状态的土地利用类型;con(si=c)表示第i个元胞邻域状态为c时则返回1,否则返回0。
土地利用转换的过程中受到自然因素、人类活动等影响,使土地利用变化过程更加复杂。为了使模型结果更加符合实际情况,反映土地变化的不确定性,因此CA中引入随机扰动因子R[17],其表达公式为:
(8)
式中:γ为0~1范围内的均匀随机变量;α为控制随机扰动大小的参数,在本文中α取值为5。
对于土地变化模拟指定相应的规则至关重要,有必要对其地表变化进行限制,转换概率主要与研究区的城市发展水平相关,例如,城市建设用地转化为草地的成本相对较高,而农用地转为城市建设用地的成本为相对较低。Liu等[18]提出每个土地利用对的转换成本(cost)是根据当地专家经验和城市规划者确定的(表1)。转换成本的值在 [0,1] 的范围内变化。较大的值表示较大的转换难度,值为 1 表示几乎不可能转换。
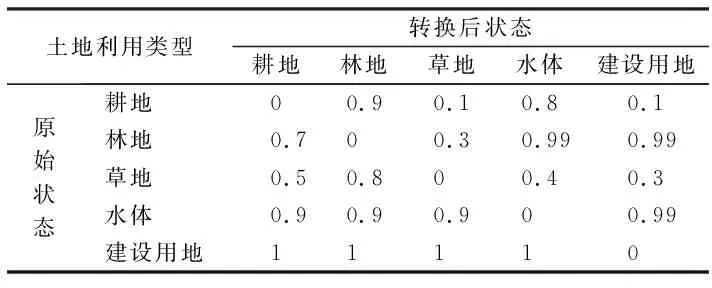
表1 土地利用各类型转换成本Tab.1 Conversion costs of various types of land use
因此,本文根据1-cost作为限制因子,根据历史时期的土地利用状态分别计算每个时期对应的限制因子,最终将多个时期限制因子进行平均计算。
考虑到近邻范围的影响、不确定因素影响及限制因素影响,通过随机扰动因子R、单元发展概率Pr、邻域因子Ω3×3(8邻域)及限制性因子L计算最终的土地利用概率Pt,其计算公式为:
(9)
3 结果与分析
本文根据提出的LSTM-CA模型,以1995—2015年土地利用及驱动因子数据作为基础,模拟2020年土地利用变化,并与MLP-CA模型结果进行对比,模拟对比如表2所示。从表2中可以看出,整体模拟结果与2020年真实土地利用分类结果相似,且2020年土地利用中建设用地呈现出增加的趋势,在实际2020年实际土地利用分布中也可以看出,建设用地面积增加,主要表现在围绕城市中心向四周扩张。为了进一步验证方法的性能,通过局部细节进行对比分析,从第3行中可以看出,LSTM-CA模拟的道路信息更加精细,相对于MLP-CA建设用地的分布更加紧凑,这主要是由于LSTM-CA充分考虑了不同时间各土地类型之间的转换关系; 另外也有效利用了路网等交通因素,同时通过观察可以发现,LSTM-CA模拟的林地噪声更少,主要是由于林地的分布相对稳定,通过多期土地利用分类数据能够有效减少林地分布的不确定性。

表2 2020年土地利用模拟结果Tab.2 Land use simulation results in 2020
为了定量检测方法的模拟结果,将模拟的各土地类型与2020年实际土地类型进行叠加分析,统计得到各类像元一致性对比情况,如表3所示。从总体预测像元数量上来看,LSTM-CA模拟的结果与实际土地利用更为接近,建设用地、耕地、草地、林地及水体的准确率分别94.03%,97.38%,66.61%,97.78%和73.83%,而MLP-CA模拟结果的准确率分别为79.99%,96.27%,67.46%,95.42%和71.32%,除草地结果基本持平外,LSTM-CA其他类别模拟精度均高于MLP-CA结果,可见LSTM-CA方法兼顾了多时期的土地利用类型变化,对于模拟的各土地利用类型像元数量更符合实际情况。
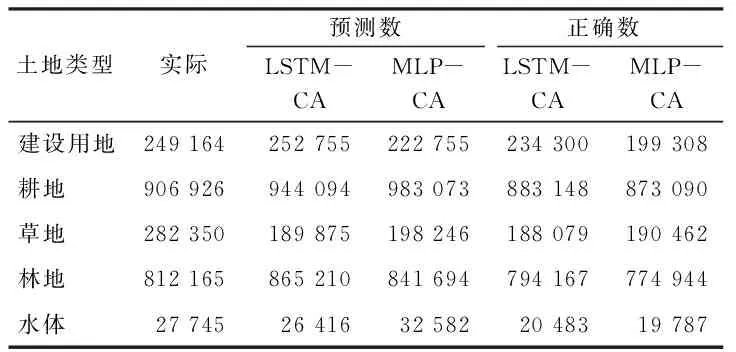
表3 2020年土地利用实际栅格与模拟栅格对比Tab.3 Comparison between actual grid and simulated grid of land use in 2020 (个)
为了更好地验证土地类型在空间上的合理性,本文将采用全局点对点的Kappa系数和变化差异对比的FoM(figure of merit)指标作为评价标准。Kappa落在(0,1)间,通常情况下认为Kappa达到0.8以上表现出较高的精度。FoM指标的计算公式为:
(10)
式中:A为实际变化但模拟结果未发生变化的单元;B为实际变化同时模拟结果也发生变化的单元;C为实际变化同时模拟结果也变化,但是变化方向不一致的单元;D为实际未变化但模拟结果变化的单元。当FoM指标大于或接近于0.21时,说明模拟结果具有一定的可信度,认为此模型具有较强的适用性。
通过对2种模拟方法进行评价指标计算,结果如表4所示。从表4中可以看出,2种土地利用模拟方法Kappa系数均达到了0.85以上,说明2种方法模拟的结果全局精度较高,而本文提出的LSTM-CA模型相比于MLP-CA方法Kappa精度提高了0.03,说明本方法在全局模拟结果上更具有优势。而FoM指标均大于0.21,并且LSTM-CA相比于MLP-CA提升了0.17,除此以外, LSTM-CA模拟结果在A,B,C,D这4个指标上均优于MLP-CA,说明本文提出的LSTM-CA方法具有较高的模拟精度,说明LSTM-CA在充分挖掘历史土地利用变化之间的关系,从而有效提升模拟精度。

表4 土地利用模拟结果精度评价Tab.4 Accuracy evaluation of land use simulation results
4 结论
本文在CA模型基础上提出了基于LSTM-CA模型用于土地利用变化模拟,以张家口市为研究区,基于1995年、2000年、2005年、2010年、2015年时序土地利用数据,结合距离变量、邻域变量及单元自然属性预测了2020年的土地利用分布情况,与MLP-CA进行精度对比分析,结果表明本文提出的LSTM-CA模型Kappa系数可达0.90,FoM指标为0.39,达到了更高精度。说明该模型能够较充分地挖掘时间序列土地利用之间的时空变换特征,通过历史时序土地利用分类数据及驱动因子构建神经网络模型计算单元发展概率,模拟未来土地利用变化。
然而LSTM-CA也存在一定的局限性,即限制规则根据前人经验获取,因此,未来将继续研究如何更加灵活地获取限制因子,同时考虑更多的驱动因素(如土地政策和社会经济等)是下一步研究的重点。
