基于ISM-SNA的城乡旧区改造后游客满意度研究
2022-12-22张名凯郑淑铭杨耀宁
韩 菡, 张名凯, 陈 杰, 郑淑铭, 刘 涛, 杨耀宁,2*
(1.云南大学 建筑与规划学院, 云南 昆明 650504;2.柏林工业大学 可持续城市发展与规划研究所, 德国 柏林 10623)
城市化发展让曾经推动社会进步的旧工业建筑面临着生存与消亡的考验[1],现阶段伴随着对旧工业建筑的研究,让此问题得以缓解。例如北京的798艺术新区、上海的8号桥等旧工业建筑区通过功能置换的现代改造,不仅延续了历史和文化情感,同时增加了建筑寿命,带动区域经济与社会效益提升,通过改造重焕活力,也获得了各界的好评[2-3]。然而总览全国旧工业园区改造,亦不乏效益不佳的项目,甚至有的项目因效益不好而进行多次改造。其中,通过对园区满意度调查和分析是一个有针对性的评价衡量方式[4]。本文在此基础上对满意度影响因素进行研究,深入挖掘影响因素之间的关系,为之后的旧工业园区改造提供建议。
在研究方法的选取上,解释结构方程模型(Interpretative Structural Modeling,ISM)作为一种研究因素之间关系的方法,现已广泛应用于各学科,如李勤等[5]基于ISM模型对旧工业建筑再利用的安全控制要素进行了研究,侯延香等[6]基于ISM模型对装配式装修发展影响因素进行了研究。通过基于ISM模型对影响因素进行研究,可以把模糊的关系转化为直观模型,从而更好地探索因素之间关系。
但由于ISM模型可能存在着级与级之间反馈困难等问题,造成部分因素之间的关联无法表现出来[7]。如能将其与社交网络分析模型(Social Network Analysis,SNA)有机结合,把各影响因素构建成一个网络,利用Ucinet软件将因素进行可视化计算与分析,可以优化此问题。运用ISM-SNA的方法对影响因素之间关系进行研究可得到更加科学的结果。
综上所述,本文将基于ISM-SNA模型对旧工业园区改造后游客满意度影响因素进行研究,希望为旧工业园区管理者和设计者提供参考。
1 研究方法及思路
1.1 解释结构方程模型(ISM)
解释结构方程模型(ISM)主要用于分析各因素之间相互影响的关系。在构建时首先通过实践经验将众多因素之间的关系进行量化并形成矩阵,之后通过计算规则建立直观的多阶结构模型,将各因素之间的关系以及结构层次直观地表达出来,便于为管理者提供决策依据。模型构建过程如下:
(1)确定邻接矩阵。将因素筛选后,根据因素数量构建n阶方阵A,对各因素之间的关系进行两两判断,因素i不影响因素j用数字0表示,因素i影响因素j用1表示。邻接矩阵A=(aij)为
(2)建立可达矩阵。可达矩阵表示各个因素之间通过一定路径可以达到的程度,通过可达矩阵可以清楚地知道因素之间的直接关系和间接关系[8]。可达矩阵M=(A+I)k+1=(A+I)k≠(A+I)k-1,式中I为单位矩阵;k=1,2,…,n(n为矩阵阶数)。
(3)因素层级划分。将可达矩阵中的可达集定义为R(Si),先行集定义为A(Si),可达集和先行集的交集定义为C(Si)。层级划分时按照不同步骤,逐次抽取因素,每一次都是一个层级关系,即按照R(Si)=C(Si)规则从上至下进行逐次抽取,然后在集合划分表中去掉该层因素,直到所有元素都抽取完成[9]。层级关系划分为
式中R(Si)为可达集,A(Si)为先行集,C(Si)为可达集和先行集的交集,E(Si)为最高集合。
(4)Micmac分析。Micmac分析方法又称为交叉影响矩阵相乘法,根据可达矩阵M判断两个因素之间的关系,判断内容包括驱动力和依赖度。Micmac分析公式为
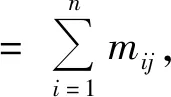
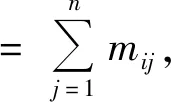
式中M=(mij)n×n为可达矩阵。
1.2 社会网络分析(SNA)
社会网络分析(SNA)是对社会关系结构及其属性加以分析的一套规范和方法,源自社会学和商业领域,它主要分析的是不同社会单位(个体、群或社会)所构成的关系结构及其属性。社会网络是由一组节点(行动者)和它们之间所有的关系组成的整体[10]。其中包含:
1.2.1 中心度分析
度数中心度。表示在网络中一个节点与其他节点直接连接的个数。度数中心度越大,表示与该点有直接联系的点越多,也说明其他相连的点受该点的影响越大。其公式为
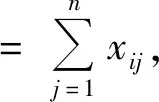
式中n为节点总数,xij表示第i节点与j是否有联结,有取1,无则取0。
中间中心度。表示网络中某点连接其他点的最短路径的数量。中间中心度数值越大,表示对其连接点信息传递的影响越大,约束控制力越强。其公式为
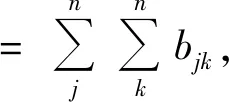
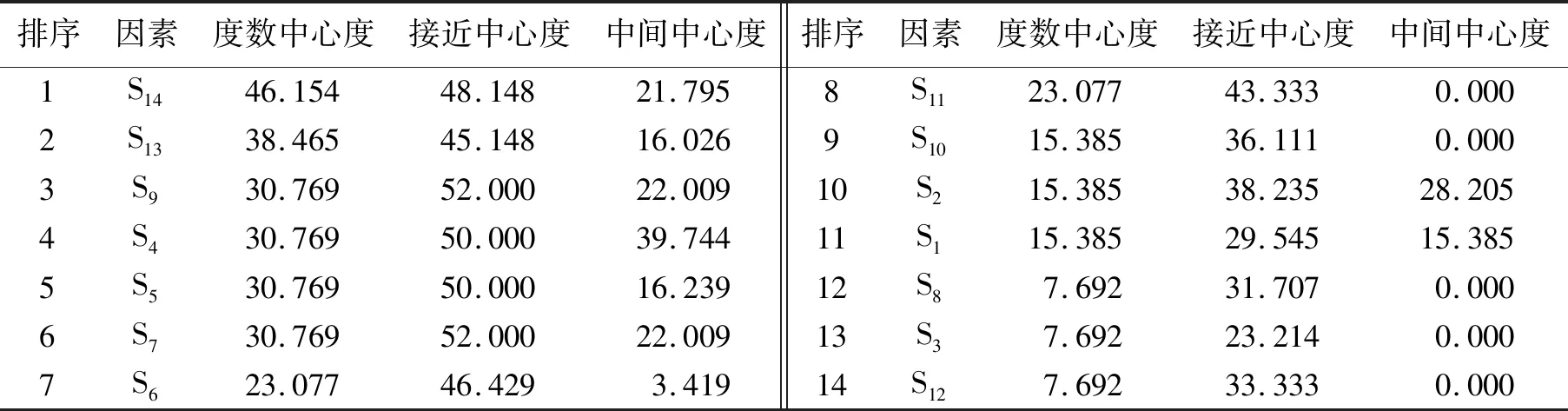
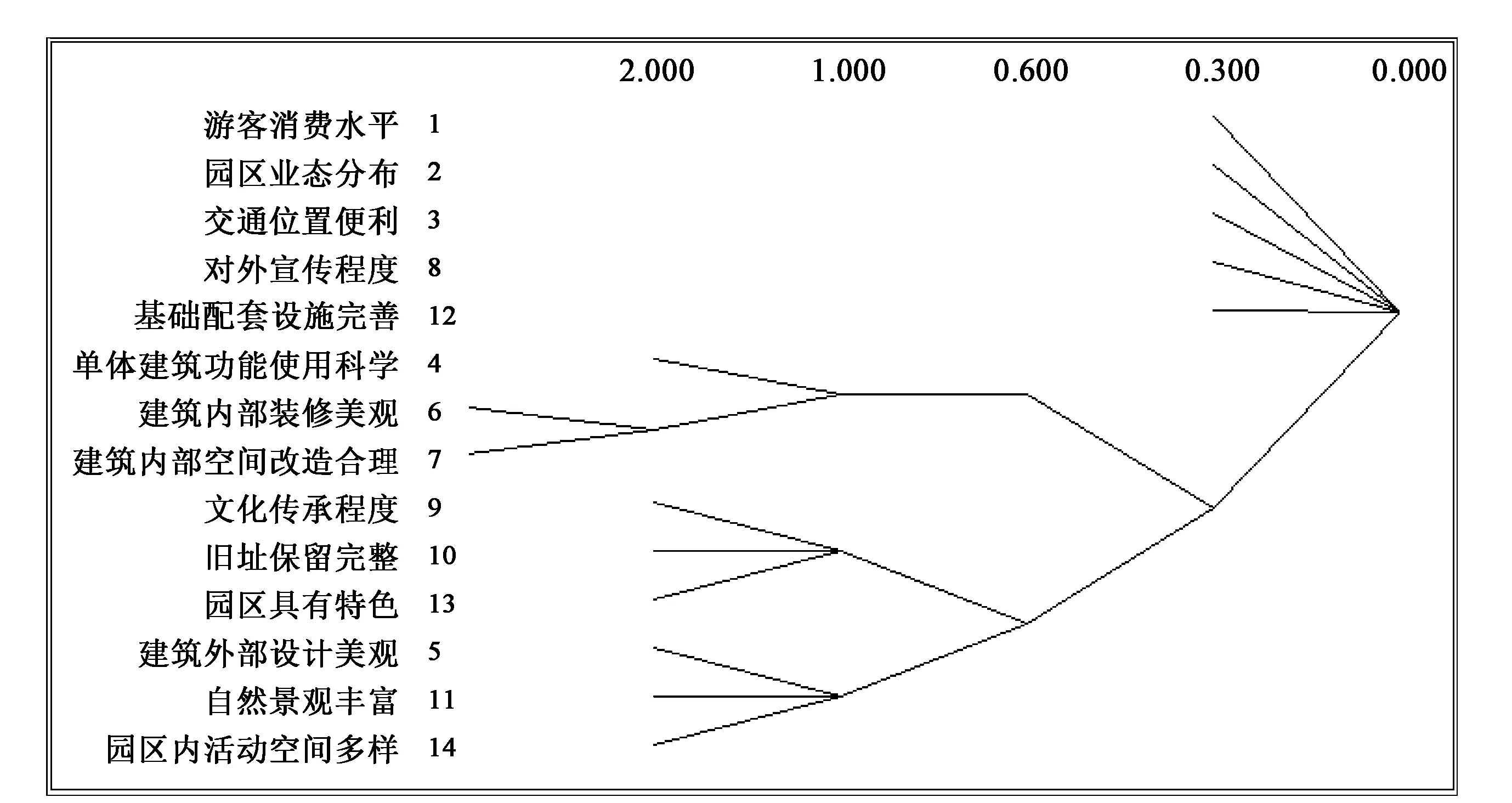
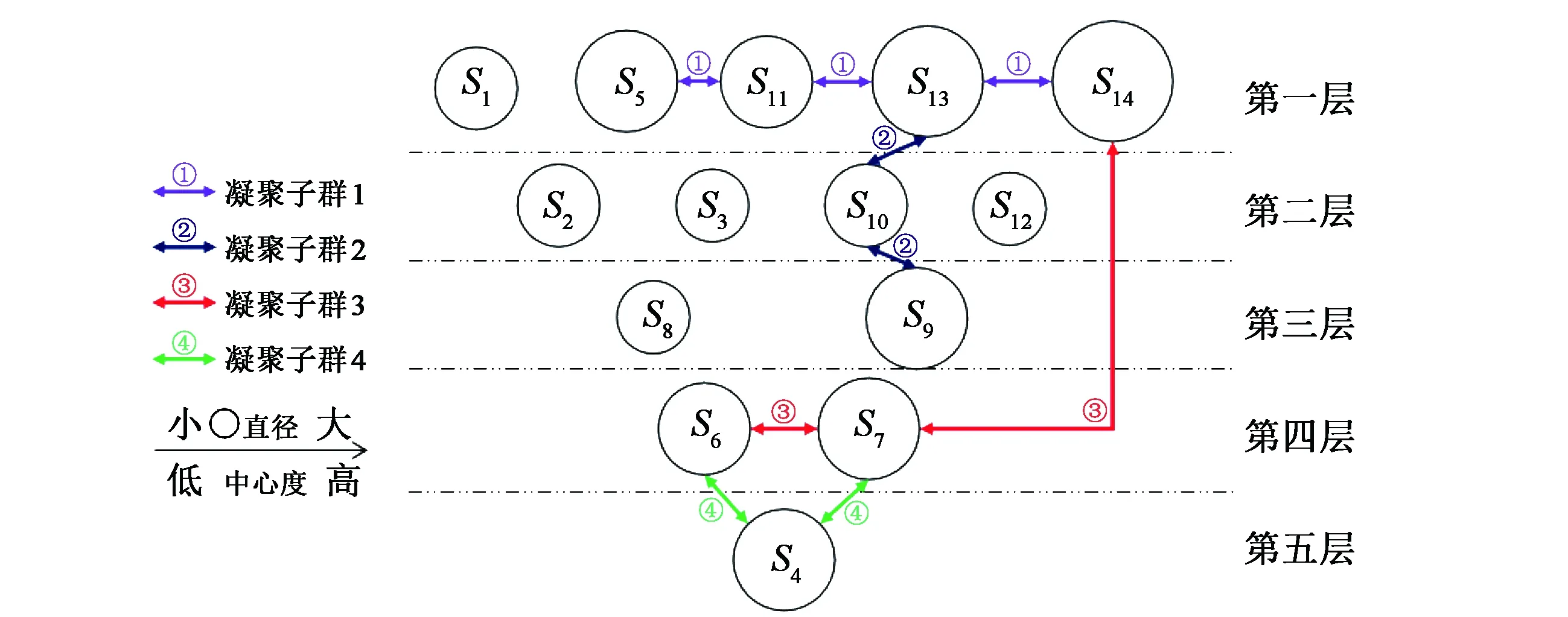
式中bjk是节点i在j和k之间捷径的概率(j,k≠i且j 接近中心度。用来测量网络中一个节点与所有其他节点距离的总和。接近中心度数值越小则距离越短,说明该节点受网络中其他节点的约束越大,自主能力越弱。其公式为 式中dij是节点i和j之间的捷径距离。 1.2.2 派系分析 派系是指建立在“伙伴”基础上的凝聚子群,是社会网络小团体层次的直接表现,最直观的理解就是一群彼此紧密相连的、有依赖性的行动者构成的群体[11]。派系分析E-I指数为 式中EL代表派系之间的关系数量,IL代表派系群体内部的关系数量,E-I∈[-1,1]。 旧工业区改造成果评价体系很多,例如李冕等[12]通过“适应性”评价为旧工业区改造更新提供依据,王丽丹等[13]通过对根源问题的探究,提出面向规划实施的,以工业遗产保护和再利用视角下的机制策略,蒲培勇[14]从价值再塑角度对工业遗产价值挖掘提供论证,谭俊涛等[15]对实施效果和初步评价进行整理。然而以上方法多从建设者和规划者角度看待旧工业区改造的问题和建立相应的评价机制,或许较为僵硬。以消费者和使用者为视角的评价体系中,武乾等[16]、贺海芳等[17]构建的旧工业园区改造后满意度评价体系以及通过实地访问游客的方式较为合适。借此,最终筛选出4大类因素:业态情况、单体建筑情况、文化情况、园区整体情况,共细分为4因子、14项影响因素,见表1。 表1 游客满意度影响因素 3.1.1 矩阵构建 (1)构建邻接矩阵。通过前文筛选的14项影响因素构建14阶矩阵,并且邀请相关专家及部分游客通过调查问卷和即时访谈等模式,进行影响因素判断,最终确定邻接矩阵为 (2)计算可达矩阵。由于邻接矩阵中各因素之间可对因果关系进行传递,构建可达矩阵M能够更好地反应各因素之间的连通程度,通过MATLAB软件以及运算规则最终得到可达矩阵为 3.1.2 层级划分 通过可达矩阵M可以求得可达集R(Si)、先行集A(Si),再通过运算规则可以得到可达集和先行集的交集C(Si)、最高集合E(Si)。最终可得旧工业园区满意度影响因素划分为5个层级,如图1所示。 图1 旧工业园区改造后游客满意度影响因素解释结构模型 第一层为S1游客消费水平、S5建筑外部设计美观、S11自然景观丰富、S13园区具有特色、S14园区内活动空间多样。综合分析可得旧工业园区改造后游客满意度提升最直接的的方式是丰富园区的自然景观,让其具有特色且美观,另一方面是增加园区内游客的活动空间以及调整游客消费水平可以直接促进游客满意度。 第二层为S2园区业态分布、S3交通位置便利、S10旧址保留完整、S12基础配套设施完善;第三层为S8对外宣传程度、S9文化传承程度;第四层为S6建筑内部装修美观、S7建筑内部空间改造合理。这些因素为中间层影响因素,较第一层影响更深入,在之后的园区提升中可根据所展示的关系进行合理调整。 第五层为最根本的影响因素,即S4建筑功能使用科学,根据此结果显示可以得知园区内单体建筑的使用方式将是影响园区满意度的根本因素,在之后的园区改造中可以吸取此经验,早期合理规划每栋建筑的使用功能。 图2 Micmac分析结果 3.1.3Micmac分析 通过Micmac计算规则得到结果如图2所示,根据图像可以清楚地看出各因素的驱动力和依赖度,其中S4单体建筑功能使用科学具有较大的驱动力,通过合理规划单体建筑的使用方式可以更好地带动其他因素提升;另一方面S6建筑内部装修美观、S11自然景观丰富、S13园区具有特色具有较大的依赖度,它们的提升需要其他因素的支撑。 由于ISM模型中邻接矩阵表示各因素之间的相互关系,而社会网络分析也是基于有向对应关系表达因素之间的相互关系,所以可以将邻接矩阵直接用来进行社会网络分析。将数据导入Ucinet软件利用Netdraw可以将因素之间的关系进行可视化呈现(如图3所示),再通过操作进行网络中心度、凝聚子群派系分析进行相关计算。 3.2.1 中心度分析 将ISM模型中的邻接矩阵导入Ucinet进行中心度计算,并将结果按照由高到低的顺序进行汇总后得到表2。可以看出中心度最高的为S14园区内活动空间多样,说明此因素在整个网络中具有较为重要的地位,在游客满意度影响度中具有举足轻重的地位,其次还有S13园区具有特色等其他因素也具有重要地位。管理者可以根据此结果在之后的园区升级中丰富园区内的游客活动空间,让园区具有自己的特色从而达到与众不同的效果。 图3 因素关系网络图 表2 中心度分析 3.2.2 凝聚子群分析 通过Netdraw将14项因素关系进行可视化后,可以看得出14项因素构成了一个因素关系网络,再根据凝聚子群的定义可知,如果在整个网络中存在着某些因素之间关系紧密,进而形成一个次级团时,称这样的团体为凝聚子群。利用Ucinet对整个网络进行凝聚子群分析得出结果如图4所示,可以得出各凝聚子群之间存在因素相互交叉的现象,表明在整个网络中没有出现凝聚子群林立的状态,整个因素网络之间的影响关系较为密切。基于此,在之后的园区改造提升中不仅可以根据凝聚子群内部关系密切的特点进行多因素共同提升,而且可以参考不同凝聚子群的共同因素进行带动提升。 图4 凝聚子群分析 图5 cliques分析 为了取消凝聚子群之间的重叠成员,利用Ucinet进行cliques分析得到结果如图5所示。其中共有4个派系,分别为(1)园区外部条件子群(紧密程度较为松散):S1游客消费水平、S2园区业态分布、S3交通位置便利、S8对外宣传程度、S12基础配套设施完善;(2)园区建筑单体子群:S4建筑功能使用科学、S6建筑内部装修美观、S7建筑内部空间改造合理;(3)园区人文特点子群:S9文化传承程度、S13园区具有特色、S10旧址保留完整;(4)园区景观子群:S5建筑外部设计美观、S11自然景观丰富、S14园区内活动空间多样。以上因素构成4个凝聚子群,说明在整个因素构成的网络中以上4个凝聚子群内部的联系关系尤为密切,在之后的满意度提升中可以将这类因素进行捆绑提升,便于可以达到更好的效果。 根据解释结构方程模型(ISM)的层级划分以及社会网络分析(SNA)得到的中心度数值、凝聚子群划分结果共同探讨,得到ISM-SNA综合影响因素网络,如图6所示。 图6 基于ISM-SNA旧工业园区改造后游客满意度影响因素分析 基于上述分析可知: (1)旧工业园区游客满意度影响的直接层面因素有5个,其中“S14园区内活动空间多样”项因素中心度最高,表明在整个影响因素构成的网络中具有非常重要的地位,所以对此因素的重视是很有必要的。其次通过Micmac分析可以得知此因素具有较强的依赖度,更需要依靠其他因素来促进S14的提升。最后根据凝聚子群分析可以得知,此因素位于两个凝聚子群内,优先考虑提升凝聚子群内的因素来带动S14的提升可获得更好的效果。 (2)“S4建筑功能使用科学”是游客对园区改造满意度影响的最深层次因素,且具有较为重要的地位,通过Micmac分析可以得知此因素具有较强的推动力,提升此因素可以促进其他因素的发展,所以主动对改造后园区内建筑的用途进行科学合理的划分将会带好较好的收益。再根据凝聚子群分析可以得知S4建筑功能使用所在的凝聚子群可以帮助更好的发展。 (3)旧工业园区改造最值得保留的是历史文化,通过ISM-SNA分析可以得知在之后的改造中除了将文化传承体现在旧址保留中,还可以将其打造成园区特色。 城乡旧区改造正在如火如荼的开展,本文对城乡旧区改造后游客满意度因素进行分析并构建相关模型,最后通过对满意度影响因素关系的研究,提出园区升级改造可参考的建议。 此外,解释结构方程模型(ISM)与社会网络分析(SNA)的结合对于因素的研究非常有效。ISM可以对因素之间的层级关系进行划分,SNA可以针对各因素之间的中心度、凝聚子群等数据进行计算,并且利用SNA分析软件Ucinet将ISM邻接矩阵可视化,两者的结合可为管理者提供量化的相关建议,提升参考价值。特别地: (1)本文在借鉴前人成果基础上,新提出了4个派系(即外部条件子群、建筑单体子群、人文特点子群、景观子群)与14个因素(即S1游客消费水平因素、S2园区业态分布因素、S3交通位置便利因素、S4单体建筑功能使用科学因素、S5建筑外部设计美观因素、S6建筑内部装修美观因素、S7建筑内部空间改造合理因素、S8对外宣传程度因素、S9文化传承程度因素、S10旧址保留完整因素、S11自然景观丰富因素、S12基础配套设施完善因素、S13园区具有特色因素、S14园区内活动空间多样因素),使得整个因素网络化更加条理化、可视化。 (2)研究表明,区内单体建筑的使用方式与园区内活动空间多样是影响游客满意度的根本因素,应当加强其重视程度,同时通过联动因素(如园区特色与建筑内部空间改造等)提升其综合品质。 (3)“建筑功能的科学使用”即建筑功能本身的科学合理设置是游客对园区改造满意度影响的最深层次因素,这要求和指导我们在建设园区整体规划和改造策略时,应该多以微观视角,重视和提高功能性需求和合理性布置。 (4)加强特色建设和文化基因传承。研究表明,历史文化是旧区改造最值得保留的重要特色。提升文化特色和历史传承不仅能坚守文化自信和文化传承的文化使命,同时从使用性角度和游客满意度角度,也是提升园区经济性和人文性指标的重要推动力。 由于本文篇幅原因和局限性,未能对现有方法进行再度优化(例如加入中间人分析法和CONCOR计算等),在接下来的研究中,将探索其与ISM模型等传统分析方法的有效结合。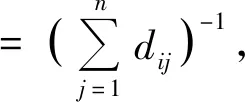
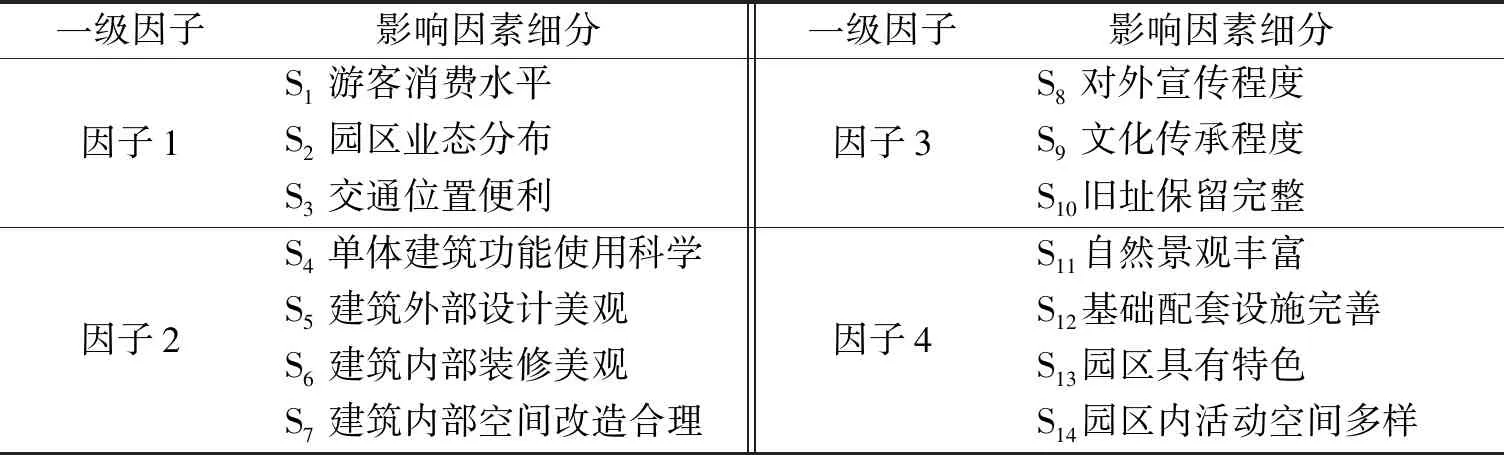
2 旧工业区改造后满意度影响因素确定
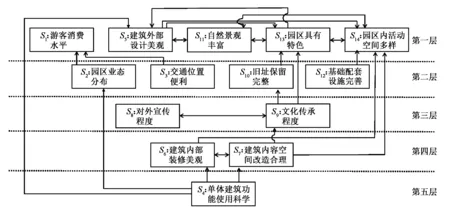
3 数据计算及分析
3.1 ISM构建及分析



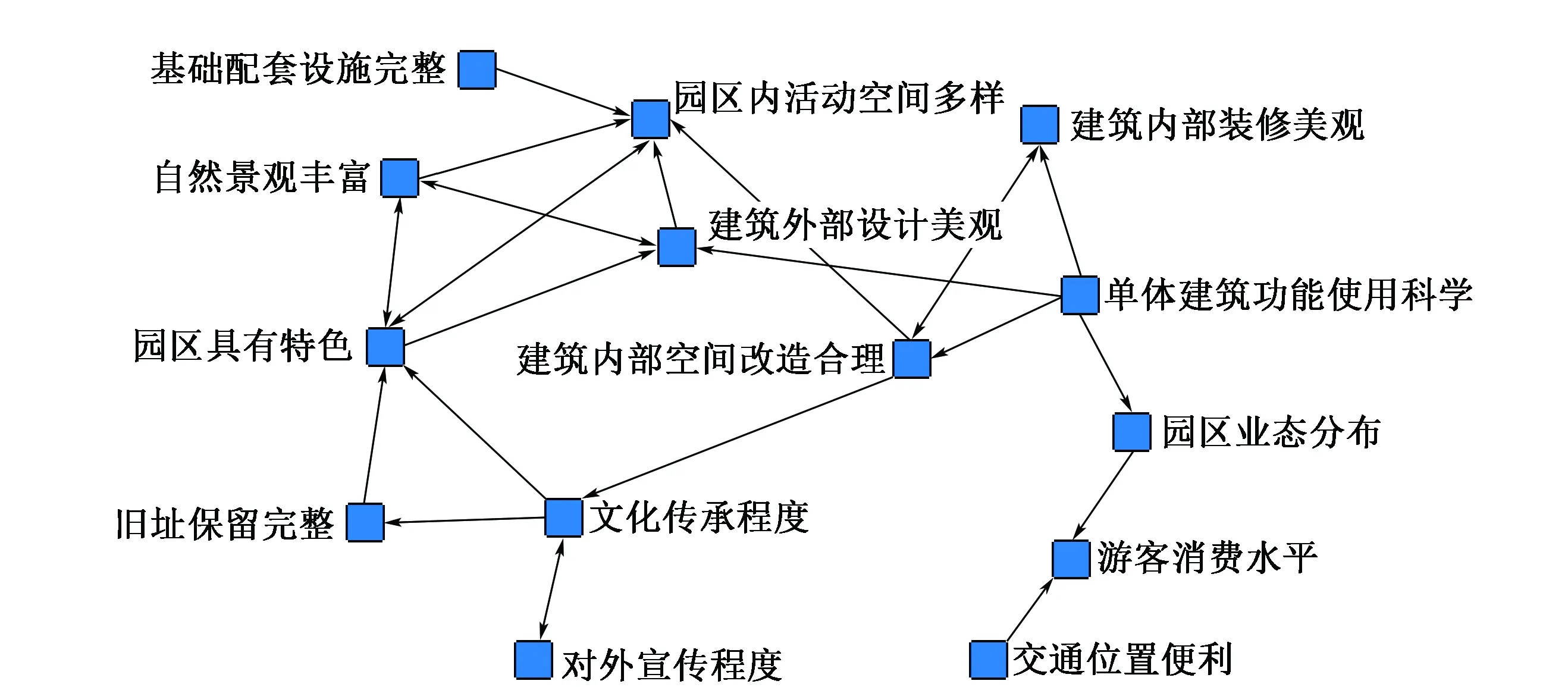
3.2 SNA计算及分析

3.3 基于ISM-SNA的满意度影响因素分析
4 结论与讨论
