基于干扰观测器的电弧炉电极滤波滑模控制
2022-12-22冯旭刚章义忠
冯旭刚, 徐 帅, 章义忠
(安徽工业大学 电气与信息工程学院, 安徽 马鞍山 243032)
电弧炉通过三相电极放电产生电弧,利用电弧辐射和电弧电流产生热量熔化炉内物料,达到冶炼金属的目的。然而,电弧炉弧长特性和控制要求随冶炼阶段的不同而不断变化,且电极短路、断弧和三相电极之间的电流耦合等干扰时常在熔炼过程中发生[1],这些复杂工况会降低电极系统工作的稳定性,造成调节时间缓慢、能耗增加,严重时会引起炼钢厂内电网电压波动和断极等严重事故发生。为此,一些学者对电弧炉电极调节系统展开深入研究,文献[2-3]采用神经网络进行解耦控制,但神经网络的自学习时间较长。文献[4]提出求解电流与弧长变化关系矩阵的解耦控制方法,但存在矩阵系数计算量过大的问题,不宜在工业生产现场应用。
滑模控制因具有强鲁棒性和抗干扰性,近年来被广泛应用于非线性系统控制[5-6]。李继超等[7]提出模糊滑模控制解决系统中参数不确定的问题,王建辉等[8]采用动态滑模控制使电极调节系统具有较好的动态品质,但上述研究都未能很好地解决滑模控制存在的抖振问题[9-10]。为此,本文在常规滑模控制的基础上,引入低通滤波器,推导低通滤波滑模控制律,解决常规滑模控制存在的抖振问题;同时设计干扰观测器对控制律进行反向补偿,削弱三相电极之前的电流耦合以及提高系统对突发性干扰的响应速度。
1 控制对象分析
在工业现场,电弧炉广泛采用的控制方案是设计3个单相回路控制器,分别对三相电极进行控制。由于电极每相在控制结构上具有相似性,本文只针对其中的一相(设为A相)进行分析。图1为电弧炉单相电极控制系统结构[7],其中整流环节检测到主电路电流信号并转换为直流信号iA,将其送入比较器与人工设定值IA比较得出电流跟踪差值信号e;差值信号送入工业现场的控制器,经由控制系统调节所得的控制输出u进入放大器触发整流电压。该电压控制电机带动电极控制系统的机械传动机构,通过电极上下调节来控制弧长L,使得电弧电流或电压维持在某一个设定值上;同时为了保证电机寿命和系统稳定性,通常需要引入速度反馈环节。

图1 单相电极控制系统示意图
为方便控制器设计,将实际生产过程中的电弧炉主电路简化为一个静态环节[11],对于持续性以及突发性大范围弧长扰动过程,采用共N段的分段线性函数将电弧炉主电路的特性G表示为
iA=G(L)=Im0-KmL+d(t),Lm 式中Im0为A相的基准电流,Km为反应不同冶炼阶段的比例系数,m表示不同的冶炼阶段;d(t)为另两相对A相的电流耦合作用,视为干扰。对电弧炉控制系统进行推导,由图1可知,从控制器输出u到电机转速v1的数学模型为 式中s代表传递函数中的拉普拉斯变量,a1和kv分别为放大器及速度反馈环节的增益,a2、T1、T2为电机特性参数。令v1=x1,那么上式可展开为 (1) 根据减速器特性可得弧长L=v1×(a3/s),a3为减速器环节增益,同时取L=x2,则减速器特性可表示为 (2) 结合电弧炉主电路模型G和整流环节特性,电弧长度L至检测电流iA的数学模型为 (3) 其中T3为表征整流特性的参数。令iA=x3,Im0+d(t)=D(t),式(3)可化简为 (4) 合并式(1)、(2)、(4)并展开可得 (5) 取x=x3并对式(5)进行整理,可得电弧炉A相电极单回路控制系统的数学模型为 (6) 根据现场实际工况数据对系统参数进行辨识选取,可得 (7) 其中控制输入u∈R,输出y∈R;θ为有界非线性函数,满足|θ|≤θmax,代表电弧炉运行过程中受到的电弧扰动及三相耦合有界干扰,控制系统的目标是通过所设计的控制律u使当前电流值iA尽可能地跟踪电流设定值IA。 为了降低滑模控制产生的抖振,设计如下低通滤波器: (8) 其中k1>0为低通滤波参数。变式(8)为 (9) 由式(6)可知τ=[x(4)-f(x)-θ]/g(x),将其代入式(9)可得 (10) (11) 利用式(11)求取虚拟控制律 对于参数λ,增大其取值可以提高系统的响应速度;然而当系统处于初始状态或需要响应较大阶跃时,此时跟踪误差较大,将导致St较大;如果仍选取较大的λ会增加系统的控制强度需求,致使执行器超幅调节(开度≥100%)。因此,应当结合系统响应时间和执行器输出范围选取合适的参数λ。对于参数η0和k1,应该先选取合适的η0取值,以获得较好的抗扰动性能,在此基础上确定参数k1以保证控制器输出抖振的消除。在实际应用过程中,留有参数λ、η0和k1的调整接口,方便操作人员在控制系统受到大的电流干扰和运动系统出现抖振时及时调整参数。 在上述低通滤波器设计中,控制律参数η的选择取决于系统在运行过程中受到的复合干扰θ,为此,本节构造模糊干扰观测器对系统干扰项θ进行观测,以实现对控制律参数的自动估计。模糊逻辑系统以推理机为基础,该推理机使用IF-THEN规则表将输入向量z∈Rn映射到输出标量y∈R,模糊系统的输出通过单值模糊化、乘积推理机以及重心法解模糊得到,基于模糊基函数的概念,模糊系统的输出可以表示为 y(z)=βTφ(z), 式中z为模糊系统的输入向量,β=(y1,y2,…,ym)T为可调参数向量,φ(z)=(φ1(z),φ2(z),…,φm(z))T为模糊基函数向量,且φ(z)的第j项为 (12) ξ=X(4)-σ。 (13) 由式(12)和(13)可得 误差ξ的时间导数为 (14) 以模糊基函数的方式表达,式(14)可变为 (15) 其中zi为模糊逻辑系统的输入,j=1,2,…,5,(c1,c2,c3,c4,c5)=(π/3,π/6,0,-π/6,-π/3),仿真过程中各控制策略参数选取见表1。 表1 控制策略参数取值 取电弧炉A相电极的初始电流为4.5 kA,因冶炼需求,此时需要将主电路电流提升至6 kA。因此在仿真时间t=5 s时,对电弧炉电极模型施加4.5~6 kA的阶跃信号;为了模拟运行中存在的耦和与突发性干扰,在t=30 s时,对仿真模型施加电流干扰D(t)=0.05×e(30-t)×sin((t-30)/3) kA,代入式(7)中。 3种滑模控制的阶跃响应如图3(a)所示,当施加幅值为1.5 kA阶跃时,本文改进滑模控制进入稳态的时间比常规滑模控制1、2分别减少4.8 s和7.9 s;常规滑模控制1、2超调量分别为0.097 kA和0.081 kA,本文改进滑模控制的超调量为0.041 kA,分别降低3.7%和2.7%。当施加干扰θ时,本文改进滑模的电流波动峰值为6.16 kA和5.93 kA,远小于常规滑模控制1、2;同时对于干扰的调节时间为9.4 s,较常规滑模控制1、2分别减少6.4 s和8.4 s,可判定改进滑模控制具有更好的动态性能。仿真中干扰观测结果如图3(b)所示。 (a)阶跃响应曲线 (b)干扰观测结果图3 仿真中阶跃响应曲线和干扰观测结果 本文改进滑模和常规滑模的控制器输出曲线如图4所示。 图4 仿真控制器输出曲线 图5 鲁棒性仿真对比结果 通过选取小参数,常规滑模控制2的输出抖振小于常规滑模控制1,但由图3分析可知常规滑模控制2的动态性能下降。观察常规滑模控制1的输出和本文改进滑模虚拟控制输出u,二者都存在非常严重的锯齿状抖振。而经由滤波器滤波后的本文改进滑模实际控制输出τ平滑无抖振,可以有效避免控制器输出抖振引起的机械结构剧烈振动,从而减轻执行器磨损,延长了系统整体寿命。 对本文改进滑模、模糊滑模[7]及动态滑模[8]进行鲁棒性仿真对比实验。在系统t=10 s时施加20%的模型不确定度,那么可得此时仿真对象为x(4)=1.2×f(x)+g(x)u。实验结果如图5所示,3种滑模控制在系统具有不确定性的情况下都能保证系统稳定性。模糊滑模的模糊规则导致控制参数多变但不精确,此时系统响应较慢,但参数多变使得模型变动时曲线波动较小。动态滑模控制响应较快但超调量变大,且模型不确定性所导致的曲线震荡也更大。本文改进滑模可以通过干扰观测器将模型变动等效为干扰,进而补偿控制输入,鲁棒性能良好。 为了能够灵活和安全地模拟电弧炉生产现场的实际工况,分别使用电感、常规电阻以及非线性时变电阻来表征变压器、短网以及电弧特性,在实验室搭建了电弧炉三相电极控制模拟实验系统。控制系统通过MATLAB和西门子S7-1200组建,MATLAB用于实现控制算法,PLC完成信号采集和控制指令发送,并使用OPC服务器实现二者之间的数据通讯。为减少电机的冲击和噪声,延长其使用寿命,在PLC和电机之间加装变频器,由变频器控制电机的驱动频率,完成三相负载回路电流的调节。 图6 模拟实验电流响应曲线 在实验过程中,对A相的可变非线性电阻进行快速调节,模拟了生产过程中单相回路受到的随机干扰,从而造成单相电流的快速变化。分别对模糊滑模控制、动态滑模控制以及本文改进滑模控制进行实验对比,实验结果如图6所示。对系统施加干扰时,采用模糊滑模和动态滑模控制策略的最大电流动态误差分别为9 A和7.5 A,而本文改进滑模控制可以将电流稳定在59~63 A,更小的电流波动在保证自身稳定工作的同时,还可以降低对其他两相电极的耦合影响,提高整体系统工作的稳定性和安全性。 本文通过设计低通滤波滑模控制器,在保持滑模控制快速性的基础上,解决了常规滑模控制存在的输出抖振问题,同时通过干扰观测器进行观测反馈,进一步增强了控制系统的抗干扰性和鲁棒性。以电弧炉为实验对象的仿真和实验结果表明,该控制算法具有更好的动态性能,为算法在类似非线性系统中的推广应用提供了依据。2 控制系统设计

2.1 低通滤波滑模设计

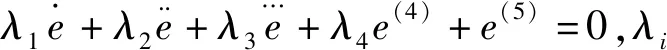


2.2 干扰观测器设计




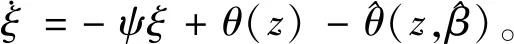



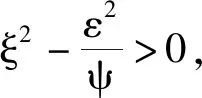
3 系统的控制策略仿真





4 工程应用

5 结论
