考虑启动时间和启动失效的核电厂冷冗余系统可靠性数值模拟方法
2022-12-22王韶轩林志贤戈道川吴洁郁
王韶轩林志贤戈道川吴 洁郁 杰
1(中国科学院合肥物质科学研究院核能安全技术研究所 合肥 230031)
2(中国科学技术大学 合肥 230026)
安全是核电产业健康发展的前提,为保障安全,核电厂大量采用冗余设计。对于一些关键设备如泵、发电机等往往采用冗余配置以满足单一故障准则[1]。这些冗余设备平时处于冷备状态(即零功率状态),只有当主件失效后才会启动,在启动过程中需要一定的启动时间且存在启动失败可能。设备的启动时间是指设备从启动到正常工作或从初始状态完全转换到另一状态所需要的时间。设备启动时间的形成原因有很多:设备的正常运行需要满足一定的条件、设备的初始状态有所限制、人的操作行为需要时间等。在启动过程中设备可能会由于自身部件老化、工作环境变化、操作行为出现失误等原因而启动失败,在核电厂中某些特定的紧急情况下,部分关键设备的启动失败被视为失效,不考虑其二次启动。文献[2]分析了核电厂中应急柴油发电机启动失效和超时的原因;文献[3]探究了核电厂水压试验泵启动失效的问题。核电厂中存在大量对反应堆安全有重要影响的冷冗余设备,针对其启动时间与启动失效进行相应的可靠性建模分析对提高核电厂整体安全性有重要意义。
在静态故障树(Static Fault Tree,SFT)分析方法中,通常不考虑设备启动时间,一般将启动失效视为基本事件以做简化处理。传统SFT模型无法有效地对核电厂冷冗余系统中蕴含的动态失效行为进行建模,国际上普遍采用动态故障树(Dynamic Fault Tree,DFT)分析方法对含有时序失效行为的系统进行可靠性评估[4‒5]。目前在DFT分析方法中,对于冷冗余设备启动时间与启动失效的处理依旧与SFT类似。针对上述问题,本文将采用蒙特卡罗数值模拟方法分析启动时间与启动失效对冷冗余系统可靠性的影响,并以核电厂应急柴油发电机组为例开展工程应用研究。
1 理论基础
1.1 动态故障树模型
DFT作为SFT的延伸,引入优先与(Priority And,PAND)门、功能相关(Functional-Dependence,FDEP)门、顺序强制(Sequence-Enforcing,SEQ)门、冷备(Cold Spare,CSP)门、温备(Warm Spare,WSP)门和热备(Hot Spare,HSP)门来描述系统中的时序失效行为[6]。图1展示了本文案例分析中涉及的三种动态门(CSP门、SEQ门和FDEP门),下面将对这三类动态门进行详细阐述。
CSP门如图1(a)所示,其包含一个主输入事件A1,两个备用输入事件A2和A3。A1开始处于工作状态,A2在A1发生失效后立即激活并转入工作状态,随后A2失效,A3被激活并转入工作状态,当A3失效时门事件发生。用割序可表示为,其中表示部件X作为Y的备件,且在备用状态下的失效率为0。
SEQ门如图1(b)所示,其包含3个输入事件A1、A2和A3,强制其门下的输入事件以从左到右的顺序发生,其割序可逻辑等价地表示为:SEQ门与CSP门的失效模式非常相似,唯一的区别在于SEQ门的输入事件可以是基本事件也可以是门事件。
FDEP门如图1(c)所示,其包含一个触发事件AT,两个相关基本事件A1和A2。当AT发生失效时,A1、A2也随之发生失效,反之A1、A2是否失效,对AT的状态没有影响。
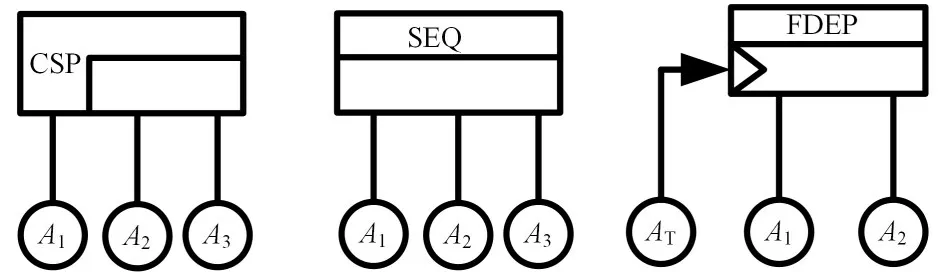
图1 动态逻辑门(a)冷备门,(b)顺序强制门,(c)功能相关门Fig.1 Dynamic logic gates(a)Cold spare gate,(b)Sequence-enforcing gate,(c)Functional-dependence gate
1.2 蒙特卡罗数值模拟
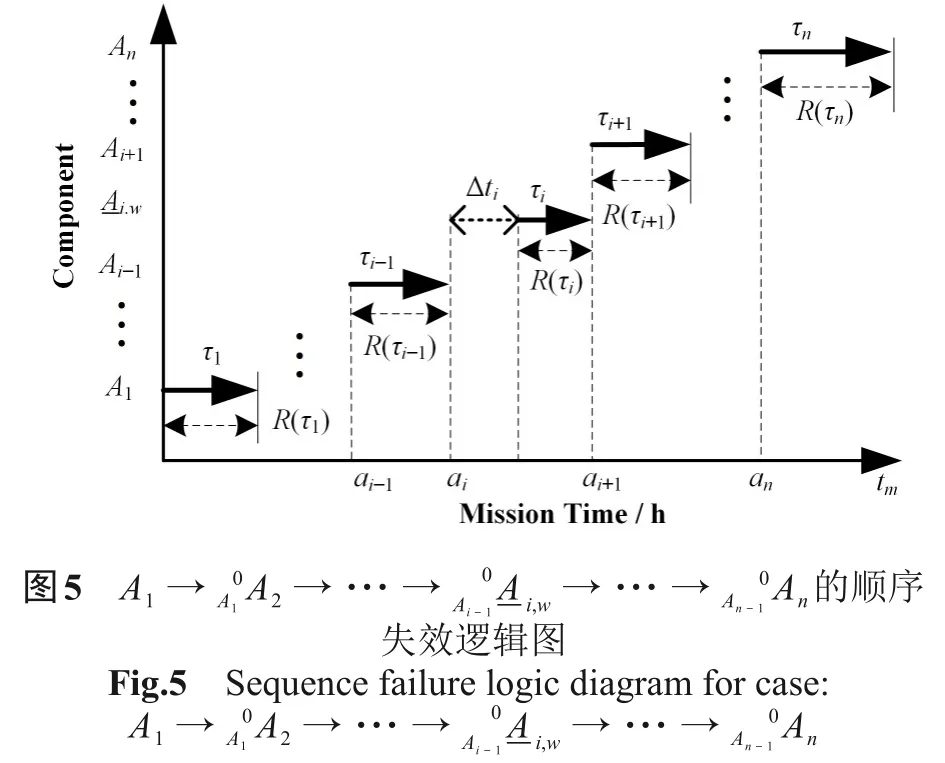
蒙特卡罗数值模拟方法的基本思想就是将解析模型转化为概率模型,通过重复构造符合一定规则的计算机随机数来求解问题[7‒8]。最小割序是指导致DFT顶事件发生的一组最少先后发生的基本事件,其状态决定系统状态。最小割序集是指所有导致DFT顶事件发生的最小割序的集合。因此,利用最小割序集可以对DFT顶事件的发生概率进行数值模拟。本文采用“最小割序集+顺序失效域”的数值模拟方法分析DFT[9]。顺序失效域则是指由图形化描述的顺序失效逻辑图所确定的带有一定顺序性的失效域[10]。以割序为例,其顺序失效逻辑图如图2所示。
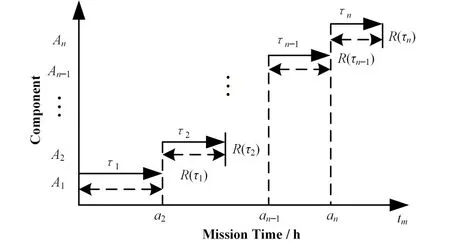
图2 A1→0A1 A2→…→ 0An−1 An的顺序失效逻辑图Fig.2 Sequence failure logic diagram for case:A1→0A1 A2→…→ 0An−1 An
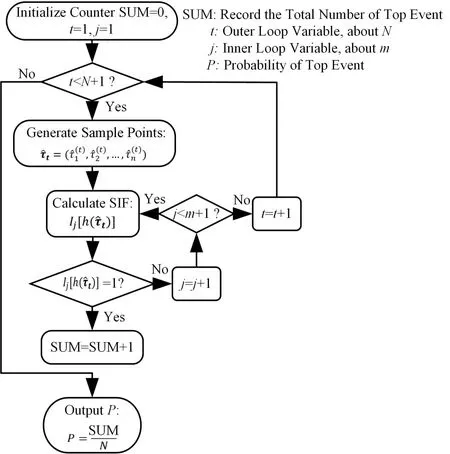
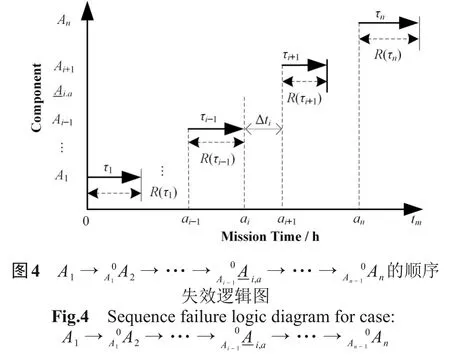
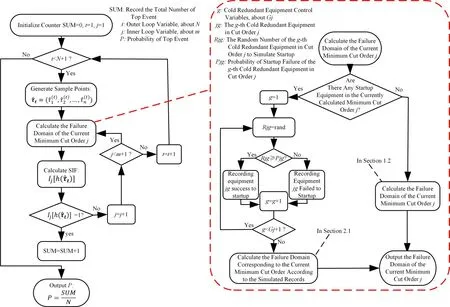
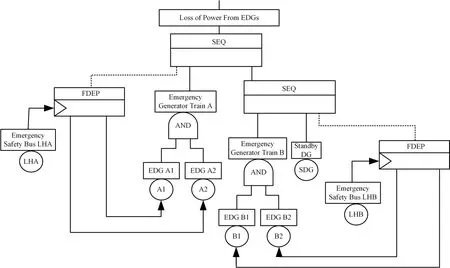
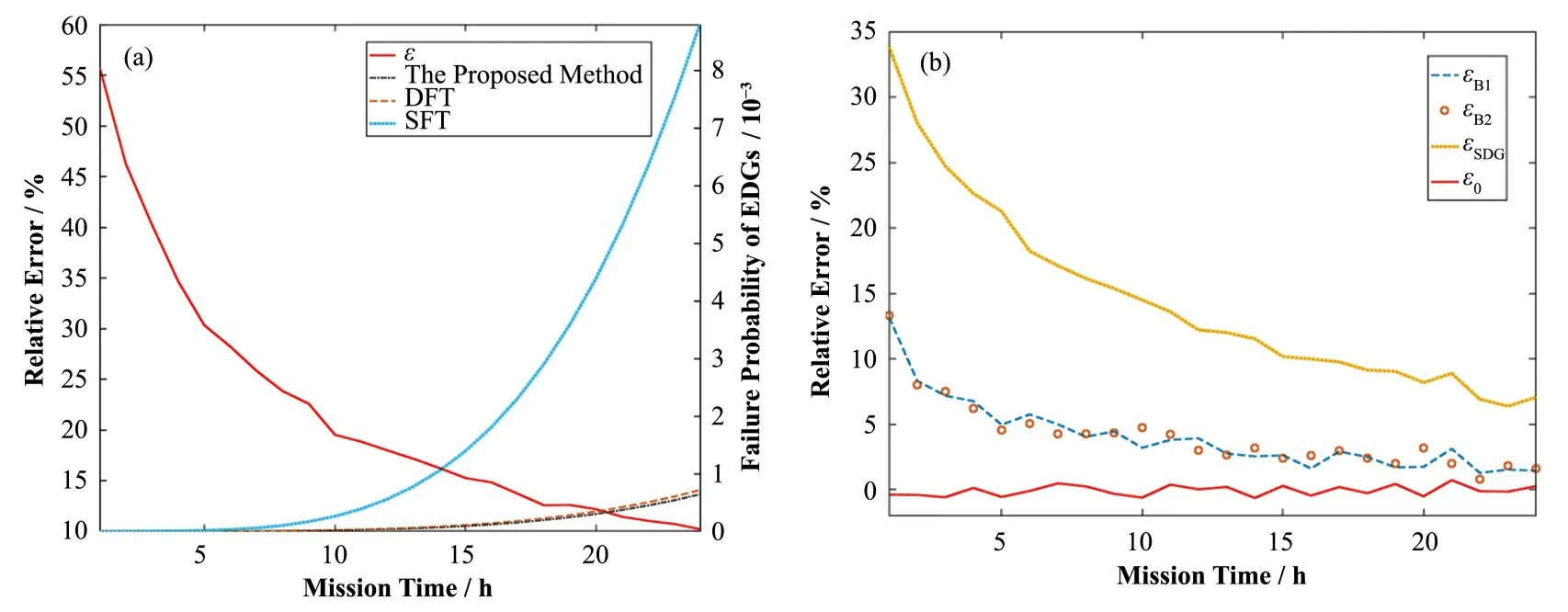
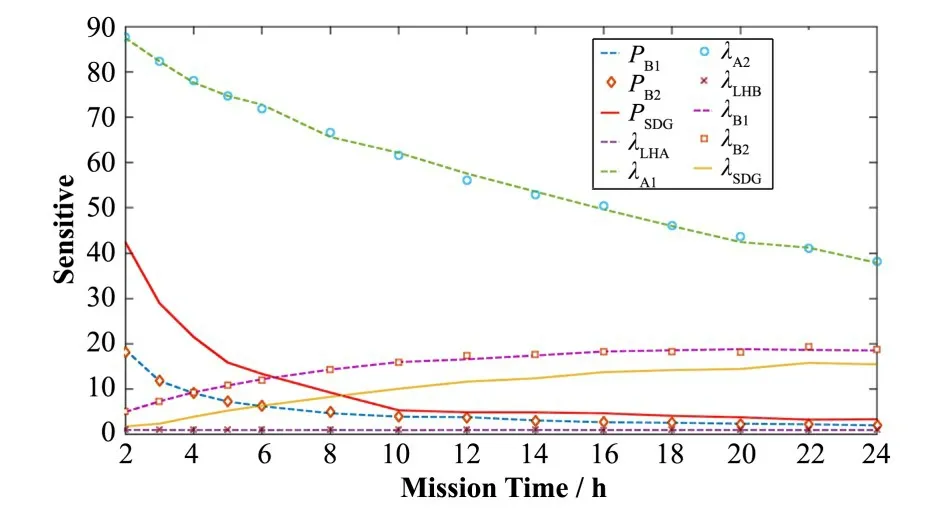
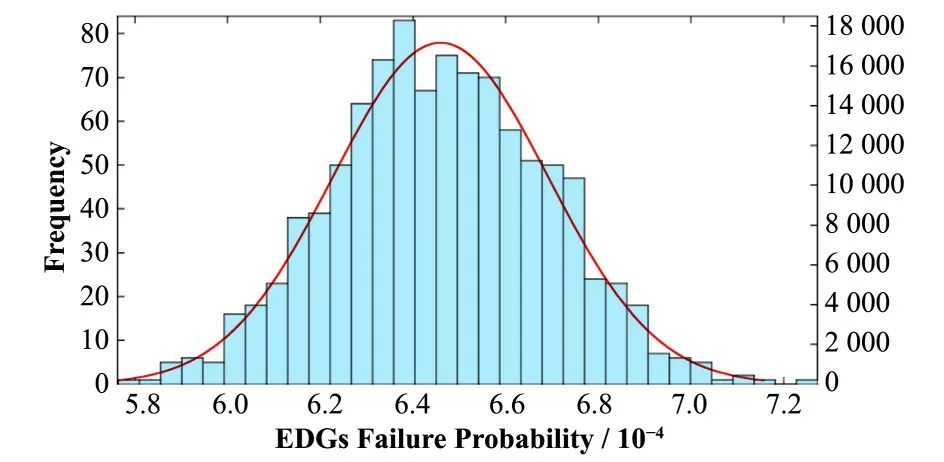
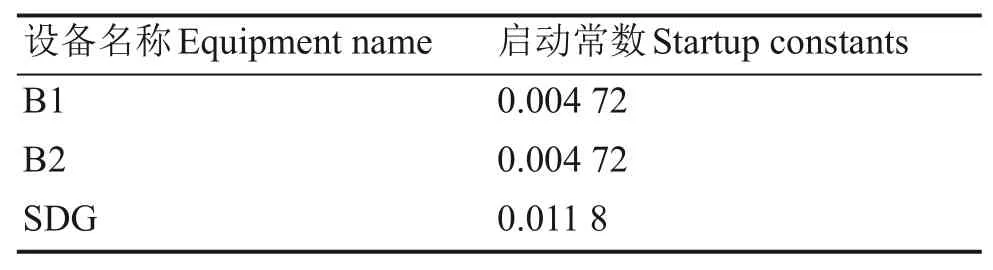
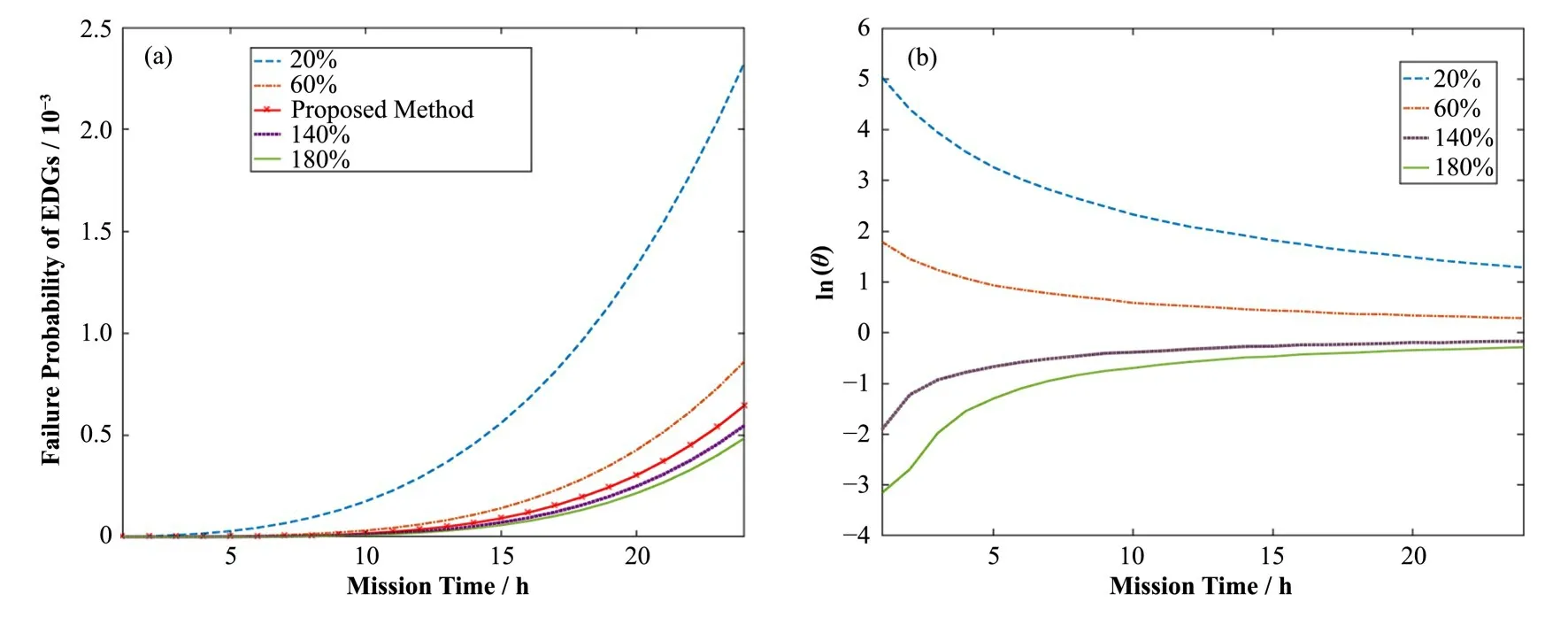
图2中,tm为任务时间;ai表示事件Ai的起始点;τi表示失效时间(即设备寿命);R(τi)表示τi的有效失效时间段,即导致割序发生的有效时间段。对于任意一个R(τi),当i=1时,R(τ1)={τ1|0<τ1 DFT蒙特卡罗数值模拟方法的主要流程为:首先根据基本事件发生的概率分布抽取随机数来判断某一时刻对应设备的状态,再结合所得随机数与最小割序的顺序失效域判断该最小割序是否发生,如果发生(即系统失效),则跳入下一次模拟;如果不发生则进行下一个最小割序的判断,以此类推,直到完成所有最小割序的判断。当模拟次数足够多时,便可根据模拟结果得到DFT顶事件的发生概率,该方法的整体流程图如图3所示。其中:N是总模拟次数,在相对误差为0.05并且置信水平为0.95的情况下即可确保模拟的结果足够可靠为事件的统计频率[11]。m表示最小割序的个数为失效时间τt=(τ1,τ2,...,τn)的第t次随机抽样样本点。割序的发生概率可以表示为: 图3 基于最小割序集的动态故障树蒙特卡罗数值模拟流程图Fig.3 Flow chart of Monte Carlo numerical simulation of DFTs based on minimum cut sequence sets 数值模拟作为一种虚拟现实技术可以直接仿真设备的启动时间以及启动状态过程,因此可用于冷冗余系统可靠性分析。 假设某最小割序为: 其中:基本事件Ai(i=2,…,n)表示冷冗余设备。下面以冷冗余设备Ai为例进行讨论,假设Ai启动时间为Δti,启动失效概率为Pi,其存在两种失效模式:1)启动未成功,即在启动过程中直接失效,用符号Ai.a表示;2)设备成功启动,在后续工作过程中发生随机失效,用符号Ai.w表示。本文中用随机数Ri=rand来模拟设备启动的结果,若Ri 针对割序: 设备Ai在启动中直接失效,不存在后续随机失效情况,其对应的顺序失效逻辑图如图4所示。由图可得,当k<i时,各基本事件的有效失效时间段表达式与§1.2中一致,可写为R(τk)a={τk|0<τk 对于割序: 设备成功启动后发生随机失效,对应的顺序失效逻辑图如图5所示。由图5可得,当k<i时,各基本事件的有效失效时间段的表达式可表示为R(τk)w={τk|0<τk R(τk)w= 因此, 的失效域Ωw可以表达为: 本方法与“最小割序集+顺序失效域”的DFT数值模拟方法类似。首先判断一个割序是否发生,如果发生则跳出本次模拟;如果不发生,则模拟下一个割序,以此类推。模拟流程如图6所示,其中:Gj表示在最小割序j中需要考虑启动时间与启动失效的冷冗余设备个数,其余符号的含义与图3一致。 图6中如何“计算当前最小割序j的失效域”为本文讨论的重点,该过程主要包括三部分:1)对最小割序进行分类;2)对设备启动过程进行模拟;3)最小割序失效域的计算。首先根据当前最小割序中是否含有需要考虑启动时间与启动失效的冷冗余设备进行分类讨论。对于不含此类冷冗余设备的最小割序,按§1.2中所提到的方法计算其失效域;对于包含的最小割序,则§2.1中的方法对所含设备的启动状态用随机数进行模拟,并记录模拟结果。最后依据模拟结果求解最小割序所对应的失效域Ωj,如式(7)所示。通过Ωj与τ̂t判断本次模拟中当前最小割序是否发生,如式(8)所示。如果发生则跳出本次模拟;如果不发生,则模拟下一个割序,以此类推。 图6 基于蒙特卡罗数值模拟的DFT中设备启动时间与启动失效建模方法Fig.6 Modeling method of equipment startup time and startup failure in DFT based on Monte Carlo numerical simulation 最终,系统的失效概率(Psystem)可计算为所有最小割序发生的次数(SUM)除于总仿真次数N。冷冗余系统失效概率的统计量表达式为: 应急柴油发电机组(Emergency Diesel Generators,EDGs)是核电厂重要的专设安全设施之一。作为核电厂内的应急电源,在丧失厂用主电源和外电源后,EDGs要及时启动为应急厂用设备供电,以保证反应堆安全停堆并防止主要设备损坏。图7展示的是某核电厂单机组的电力供应系统结构简图[12]。其中EDGs共包含5台柴油发电机(4台常规柴油发电机+1台备用柴油发电机)。4台常规柴油发电机被分为两个应急发电机组:应急发电机组A(包含柴油发电机A1与柴油发电机A2)和应急发电机组B(包含柴油发电机B1与柴油发电机B2)。 图7 某核电厂简化电力供应系统图Fig.7 System diagram of simplified power supply for nuclear power plant 丧失场外电事件发生后,首先启动A,此时B处于冷备状态。A可能会由于自身发生随机失效或者应急安全母线LHA故障而失效。当A失效后,B才会启动。同样地,B可能会由于自身发生随机失效或者应急安全母线LHB故障而失效[13]。当A、B都失效后备用柴油发电机才会启动,当备用柴油发电机也失效后,SBO事故发生。在这种情况下EDGs的故障顺序是:首先A发生失效,接着B启动并失效,最后备用柴油发电机启动并失效,SBO事故发生。本文将使用DFT对系统顺序失效行为进行建模,并将在§3.2中进行详细说明。 应急发电机组B与备用柴油发电机平时处于冷备用状态,由于发电机组放置区域、人员的操作和设备的状态等一系列不确定性因素,到备用柴油发电机真正投入使用需要一定的启动时间Δt。在核电厂运行的历史上曾出现过应急柴油发电机启动失败的案例[14−15]。启动油量的控制[2]、快速启动导致的柴油发电机老化[16]、系统接线和现场布置错误[17]等都是影响柴油发电机能否正常启动的因素。本文假这些处于冷备状态的柴油发电机具有一定的启动失效概率P。EDGs中相关设备的失效参数参考文献[12]与[13],具体如表1所示。以EDGs供电失效为顶事件,根据§3.1中描述的失效行为对系统进行DFT建模分析,DFT模型如图8所示。SEQ门表征EDGs备件中存在的强制顺序失效行为,FDEP门表征LHA/LHB与A/B之间的依赖关系。 图8 EDGs的DFT模型[13]Fig.8 DFT model of EDGs[13] 表1 EDGs设备的失效信息Table 1 Failure information of EDGs 3.3.1失效概率对比分析 采用所提方法、传统DFT方法和SFT方法分别计算EDGs在任务时间t=24 h内的失效概率,并着重比较了所提方法与传统DFT方法的计算差异,即两种方法所得结果的相对误差ε=(PD−PP)/PD×100%,其中:PD为传统DFT方法的计算结果;PP为所提方法的计算结果;ε计算结果如图9(a)所示。计算平台为MATLAB软件,样本数的设置同§1.2一致,事件的统计频率Pf用传统DFT方法对应的结果做代替。从图9(a)可以看出,由于考虑了柴油发电机的冷备特性与启动时间,本文所提方法得到的系统失效概率较SFT与传统DFT方法更低。由于考虑了启动时间,本文所提方法的计算结果较传统DFT方法有明显的改善,尤其是在任务初期。启动时间所产生的影响有限,且随着任务时间的增加ε不断减小,在24 h时,ε=10.20%。此外,本文进一步探究了影响此概率差的因素以及这些影响因素单独所占的份额,结果如图9(b)所示。εB1、εB2和εSDG分别表示只考虑对应柴油发电机启动时间时,所提方法与传统DFT方法计算结果的相对误差;ε0则表示不考虑启动时间时的相对误差。从图9(b)可以看出,在不考虑启动时间时,本文所提方法与传统DFT方法结果一致,即所提方法中对启动失效概率的处理符合传统方法中“将设备的启动失效视为基本事件”的假设,因此两种方法的结果差异来自于启动时间。而在B1、B2和SDG这三个设备的启动时间中,SDG的启动时间对结果的影响最大。 图9 EDGs失效概率对比分析(a)失效概率对比,(b)设备启动时间对EDGs失效概率的影响Fig.9 Comparison of EDGs failure probability(a)Failure probability comparison,(b)Effect of equipment startup time on EDGs failure probability 3.3.2参数敏感性分析 为了评估各参数对系统失效概率不确定性贡献的重要程度,本文对EDGs中相关参数进行了敏感性分析,计算公式如下所示: 式中:RU为参数X的值是原来的10倍时系统失效概率;RL为参数X的值是原来的0.1倍时系统失效概率。SX为参数X的敏感度,当SX>1,表示该参数对系统失效具有正面影响,而SX越偏离1表示参数对系统失效概率的影响越大。图10展示了在任务时间24 h内设备参数的敏感度变化曲线,表2为各参数在t为2 h和24 h时对EDGs系统失效概率的敏感度及其排名,其中PB1、PB2和PSDG分别表示对应柴油发电机的启动失效概率;λLHA和λLHB分别表示应急安全母线LHA和LHB的失效率;λA1、λA2、λB1、λB2和λSDG分别表示对应柴油发电机的失效率。 图10 设备参数的敏感度变化曲线Fig.10 The sensitivity change curve of equipment parameters 由图10和表2可知,在初始阶段“λA2”和“λA1”是最敏感的参数,敏感度为88.02和87.32。启动失效参数“PSDG”、“PB1”和“PB2”分别排在第3、4、5位,敏感度为42.38、19.08和18.13,对系统的失效有显著影响。随着任务时间的增加,在24 h时最敏感的参数为“λA2”和“λA1”,敏感度为38.45和37.89。排在第3位和第4位的则分别是“λB2”和“λB1”。而启动失效参数“PSDG”、“PB2”和“PB1”分别排在第6、7、8位,敏感度为3.38、2.17和2.09。综上所述,由于启动相关参数是固定值,因此在初始阶段对结果影响较大,随着任务时间的增加,影响逐渐减小。因此,提高柴油发电机的启动可靠性尤其是在初始阶段,对提高EDG的整体安全性具有重要意义。 表2 EDGs设备参数的敏感性指标Table 2 Sensitivity index of EDGs equipment parameters 3.3.3不确定性分析 考虑到设备启动时间的随机性,本文对EDGs失效概率进行不确定性分析。假设设备启动时间服从正态分布,具体如表3所示。系统任务时间设置为24 h,通过抽样程序获得1 000组启动时间的样本,然后将每一组样本输入到所提方法的计算模型中产生一个随机输出样本(EDGs失效概率)。最后将1 000个EDGs失效概率绘制成频率直方图,如图11所示。 表3 启动时间的分布参数Table 3 Distribution parameters of startup-time 图11 EDGs失效概率的频率直方图Fig.11 Frequency histogram of EDGs failure probability 从图11可以看出,EDGs失效概率服从正态分布。表4展示了EDGs失效概率均值、标准差以及对应的置信区间。由表4可知,在24 h内EDGs发生失效的概率的置信水平为95%的置信区间为(6.445~6.474)×10−4。 表4 参数估计结果Table 4 Results of parameters evaluations 3.3.4启动特性对结果的影响 根据国内外核电站运行经验,适当延长柴油发电机启动时间,有利于降低其启动失败概率,延长运行寿命[16]。因此,本文假设柴油发电机的启动时间与启动失效概率成反比,即启动时间与启动失效概率的乘积为一个定值K,本文称之为启动常数,具体如下所示: 式中:Δt为启动时间;PΔt为Δt时间内的启动失效概率。K可以通过设备当前的启动时间和启动失效概率乘积获得,如表5所示。为评估启动特性对EDGs失效概率的影响,启动时间分别选取为表1中启动时间的20%、60%、140%和180%。计算EDGs在任务时间t=24 h内的失效概率,并与原结果进行比较,如图12(a)所示。由于在不同启动时间下系统失效概率间的数值差异过大,为了更直观地比较系统失效概率变化趋势,本文采用对数ln(θ)来展示,具体如图12(b)所示,其中θ=PX/PP;PX为基于新的启动参数的计算结果。可以看出,在任务初期,启动时间变化对结果有较大影响,且随着启动时间的延长,系统失效概率随之降低。 表5 设备的启动常数Table 5 Startup constants of equipment 图12 启动特性对EDGs失效概率的影响(a)不同启动时间下的概率值,(b)不同启动时间下的ln(θ)值Fig.12 Effect of startup characteristics on EDGs failure probability(a)Probability under different start time,(b)ln(θ)under different start time 本文重点研究了备用设备启动时间与启动失效对冷冗余系统失效概率的影响,提出了一种冗余系统可靠性数值模拟方法,利用所提方法对核电厂EDGs失效概率进行了分析。案例结果分析表明:1)本文所提方法能够对以往方法无法考虑冷备件启动时间耦合启动失效的问题进行建模分析,从而能更加准确地反映冷冗余系统的实际运行状态与真实的失效场景;2)启动时间对结果影响在任务早期较大,后随任务时间的增长而减小;3)设备参数的敏感性分析为后期提高系统可靠性提供了理论依据;4)在24 h内EDGs发生失效的概率的置信水平为95%的置信区间为(6.445~6.474)×10−4;5)适当延长柴油发电机启动时间有利于降低EDGs系统的失效概率。本文中案例的计算结果展示了该方法在精确建模与释放保守风险方面的潜力,未来将针对核电厂复杂系统开展更为详细的建模研究。 致谢感谢中国科学院合肥物质科学研究院核能安全技术研究所公共技术中心提供测试平台。 作者贡献声明王韶轩:起草文章、统计分析、设计分析案例;林志贤:技术支持、分析数据;戈道川:审阅文章内容、技术指导;吴洁:审阅文章内容;郁杰:形式检查、方向指导。
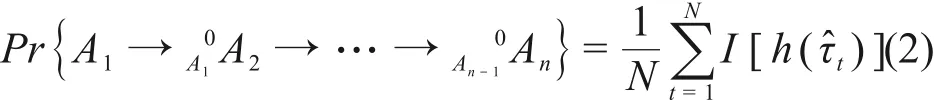
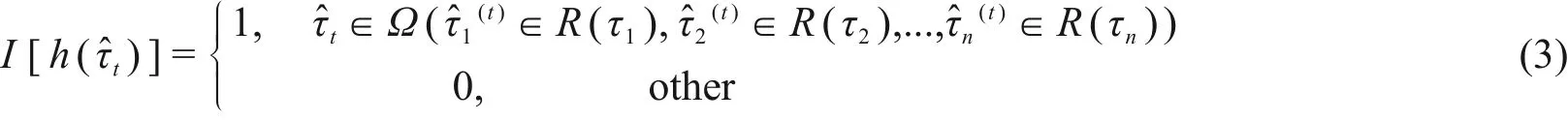
2 考虑设备启动时间与启动失效的冷冗余系统可靠性数值模拟方法
2.1 包含冷冗余设备的割序失效域


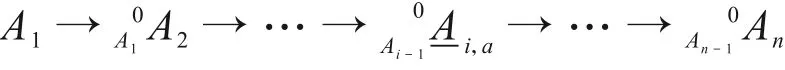
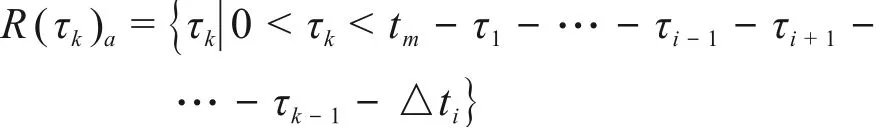
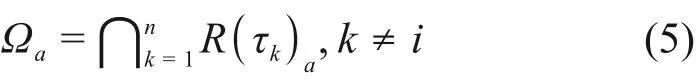
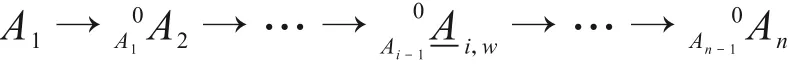
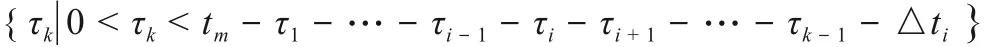

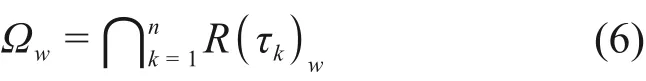
2.2 基于最小割序集的数值模拟方法

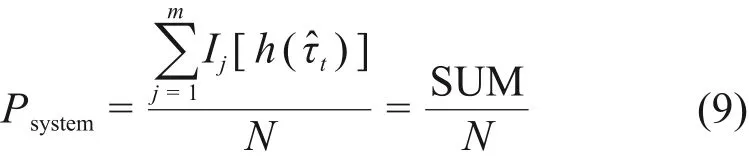
3 案例分析
3.1 事故描述

3.2 应急柴油发电机系统的动态失效模型及设备失效参数

3.3 计算分析





4 结语
