遗传算法在板式定制家具混合流水车间调度中的应用

2022-12-22陈星艳戴向东黄艳丽欧阳周洲郝绍平詹秀丽

家具与室内装饰 2022年11期

■王迅，陈星艳，陶涛，戴向东，黄艳丽，欧阳周洲，郝绍平，詹秀丽，吕宙

(1.中南林业科技大学，湖南长沙 410004；2.农林生物质绿色加工技术国家地方联合工程研究中心，湖南长沙 410004；3. 木竹资源高效利用省部共建协同创新中心，湖南长沙 410004；4.欧派家居集团股份有限公司，广东广州 510000）

随着板式定制家具的流行，企业生产通常采用“多品种小批量”的个性化定制生产模式。但由于个性化定制产品结构和外观的多样性，且家具车间调度大多凭借经验进行[1-3]，给企业的生产带来了一定难度，造成了生产效率低下等现象。定制家具的个性化与生产高效性之间的矛盾是定制家具行业急需解决的难题[4-6]。

遗传算法是通过模拟自然界中遗传机理和自然选择过程而提出的，其优点在于在全局解空间具有良好的搜索性能以及自适应优化等特点，广泛应用于调度领域[7-8]。本文利用该算法解决板式定制家具相同并行机混合流水车间调度问题，优化目标函数为最小化最大完工时间，以期提高车间生产效率和设备资源利用率，为车间提供科学的调度方案，从而一定程度上解决定制家具产品个性化与生产高效性之间的矛盾。

1 板式定制家具相同并行机混合流水车间调度问题

1.1 问题描述

■图1 板式定制家具相同并行机混合流水车间布局图

板式定制家具相同并行机混合流水车间调度问题（HFSP）可以描述为：n个具有相同加工路径的板件经过m道工序进行加工，至少有一个加工工序的并行机器数量大于1，且同一工序并行机的处理性能完全相同，示意图如图1所示。已知所有板件的加工时间，问题的目标是要确定n个板件在每个加工工序的加工顺序以及对应的设备分配方案，从而使得所有板件的最大总完工时间最小[9-11]。问题的假设条件如下：

（1）一个板件同一时间不能在多台设备上进行加工；

（2）每台设备同一时间只能加工一个板件；

（3）每个板件在设备上的加工时间已知，且加工时间因板件类型的不同而不同；

（4）同一板件的工序之间存在先后约束关系，不同板件的工序间不存在约束关系；

（5）在同一台设备上切换板件的调机时间算在加工时间内；

（6）不同工序之间有无限的缓冲区间[12]；

（7）忽略设备故障等问题。

1.2 问题建模

有关变量如下，记n为板件数，j为板件序号，m为工序数，i为工序序号，q为机器序号，Pji为板件j在工序i加工所需的加工时间，Sji为板件j在工序i的开始加工时间，Fji为板件j在工序i的完工时间，mi为工序i的并行机数量，Cmax是所有板件的最大总完工时间，设置整个生产的开始时间为0，L是一个很大的常数。同时定义以下两个变量：

建立板式定制家具车间带相同并行机的混合流水车间调度数学模型如下：

上述数学模型的优化目标是使得最大总完工时间最小化，即式（1），对于板式定制家具相同并行机混合流水车间调度而言，就是要确定板件在各个工序的加工顺序，以及每个工序的设备分配情况，使得Cmax最小。其中：式（2）表示所有板件的最大总完工时间等于板件j在工序i的完工时间集合中最大的那个数；式（3）用来计算每个板件在任何一个工序的完工时间；式（4）保证每个板件在每个工序只能由该工序的一台设备加工；式（5）保证每个板件必须在上一道工序加工完成后才能开始现工序的加工；式（6）和式（7）是对设备加工容量的约束，即同一台设备不能同时加工两个板件；式（8）是变量约束。

2 板式定制家具相同并行机混合流水车间调度遗传算法设计

2.1 算法原理

遗传算法是通过模拟自然界中遗传机理和自然选择过程而提出的搜索算法，包括繁殖、杂交和突变等现象[13]。求解流程如图2所示。

2.2 算法设计

2.2.1 染色体编码

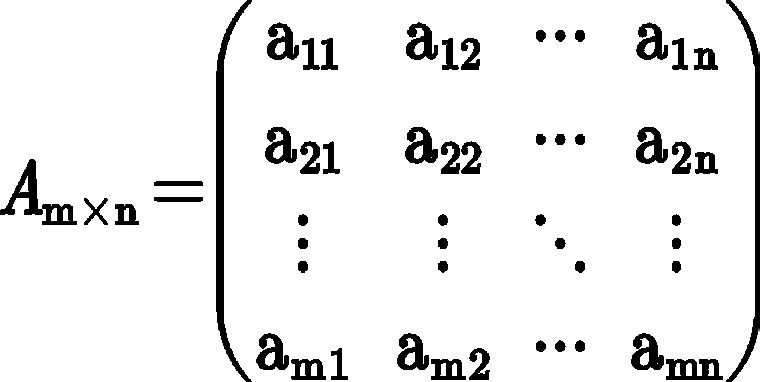
假设要加工n个板件，每一个板件要经过m道工序，每一道工序的并行机数量为mi。构造一个n×m的编码矩阵如下所示：

■图2 遗传算法流程图

其中，行表示工序过程,列表示工件序号，染色体基因aij携带第i道工序中板件j在哪一台机器上被加工的信息。通常aij由整数和小数两部分组成,整数部分表示板件j在工序i的加工设备序号，小数部分表示在同一台设备上加工发生冲突后的先后顺序，数值较小的优先被加工[14]。

因此，在上述矩阵编码的基础上可以构造算法的染色体：由m段组成，每一段表示不同的工序，用标识符“0”隔开，每小段含有n个基因，因而每个染色体长度为m*(n-1)。可用下述矩阵表示：

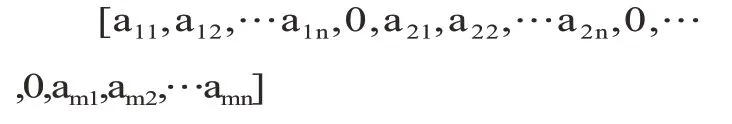
2.2.2 种群初始化和适应度函数确定

本文采用产生随机数的方式来产生初始解。在本文的车间调度模型中，目标函数是寻求所有板件加工完工时最小的总完工时间。因此，本文以最大总完工时间即Cmax的倒数作为适应度函数，即适应度函数F = 1/Cmax。

2.2.3 选择操作

本文采用二元锦标赛选择法，即在当前所选择的种群中随机选择两个个体为一组，通过比较，适应度较大个体被选择进入下一代进行运算，该策略可有效保留非最优个体，有效提升算法的全局搜索性能[15]，从而避免陷入局部最优解。

2.2.4 交叉操作

本文中首先依据一定的交叉概率从种群中随机选取两个个体作为父代，并随机选取两个不同的基因位置，将两位置之间的基因进行互换，再根据原有的父代基因排列顺序填补交叉部分中遗失的基因。例如：

随机选取两个父代染色体为：

随机选取两个不同的基因位置进行交叉操作：

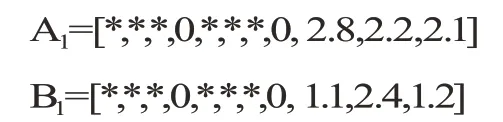
补齐空位后得到子代染色体为：

2.2.5 变异操作

本文中染色体变异方式为单点基因互换，可避免由于交叉操作引起的某些基因的永久性丢失[16-17]，防止算法过早收敛和陷入局部最优解。例如：

若父代染色体为：

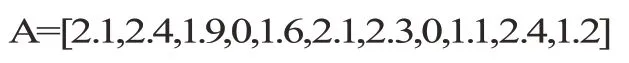
随机产生两个正整数r1=4，r2=6，进行基因互换得到子代染色体为：

3 实例仿真

本文以某个时期内某一板式定制家具车间生产的一批订单为例，选取这一批次开料后的15块需要排钻的板件（分别编号为1-15），这15块板件经过相同的4道生产工序。开料工序由1台电子开料锯进行加工，封边工序由2条加工能力相同的柔性封边线进行加工，排钻工序由2台加工能力相同的六面钻进行加工，包装工序由1条自动包装线进行加工，各板件在不同工序上的加工时间如表1所示（表内的单位为秒），求这15块板件在各个工序上的加工顺序。

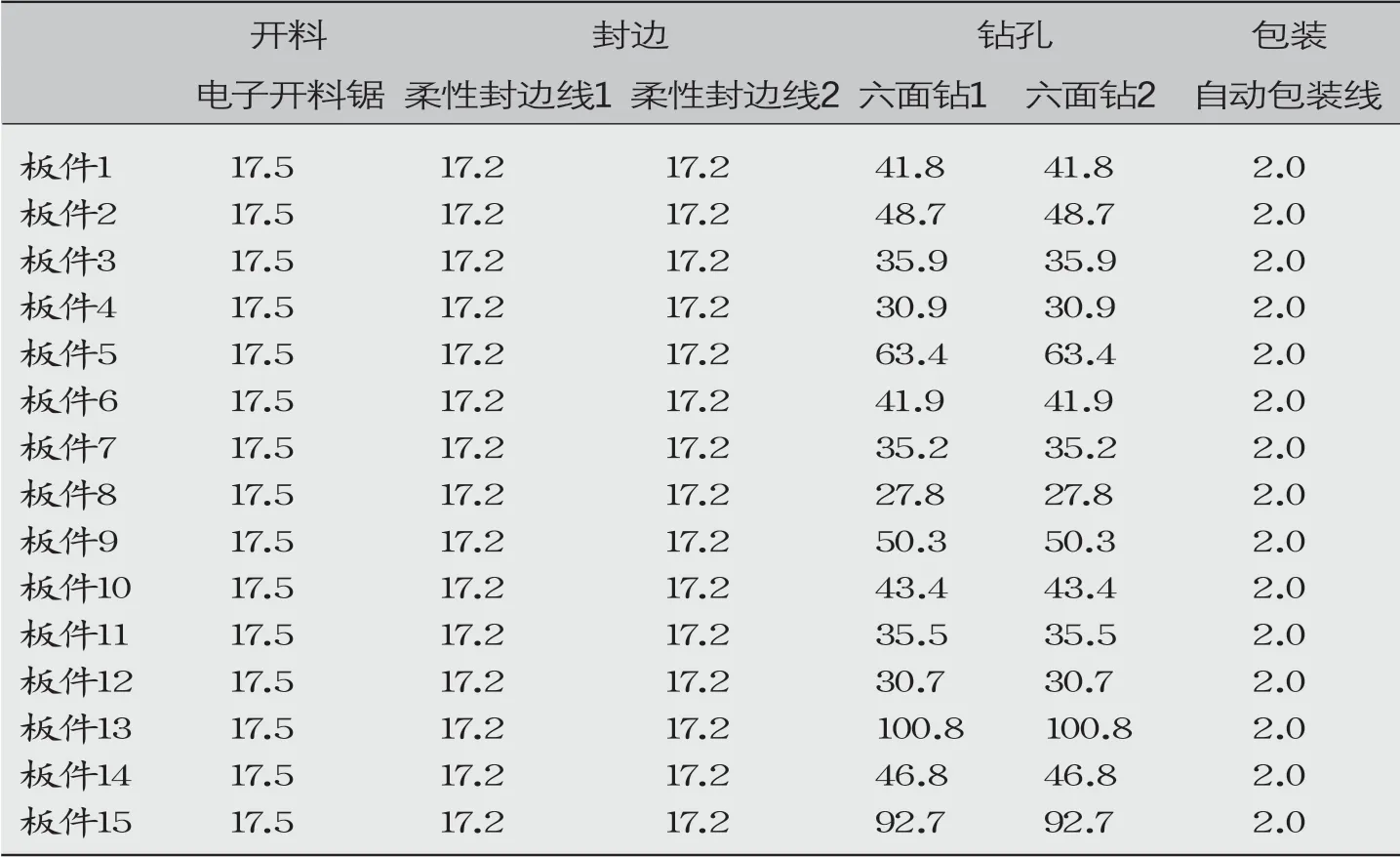
表1 各板件在各工序上的加工时间表

用python编写上述遗传算法的程序。其中，参数的选择大多依靠经验值：（1）种群规模太小时，会导致精度不足且解不稳定，种群规模越大时，虽然越可能找到全局解，但是太大的话会导致性能下降、运行时间变长，一般取20-100；（2）迭代次数太小时，种群还未成熟，算法不容易收敛，迭代次数太大时，算法会早熟，继续进化只会增加运行时间和资源浪费，一般取100-500；（3）交叉概率太小时，无法有效更新种群，当交叉概率太大时，随机性增大，容易错失最优个体，一般取0.4-0.99；（4）变异概率太小时，会大大降低种群多样性，丢失一部分有效基因且不易修复，变异概率太大时，可保证种群多样性，但容易使算法发生退化，一般取0.0001-0.1。本文中，选取种群大小N=20，迭代次数M=400，交叉概率pc=0.6，变异概率pm=0.1。

为确保该遗传算法的有效性，本文对遗传算法进行10次独立实验，结果记录如表2所示（表内的单位为秒）：

表2 运行结果记录表

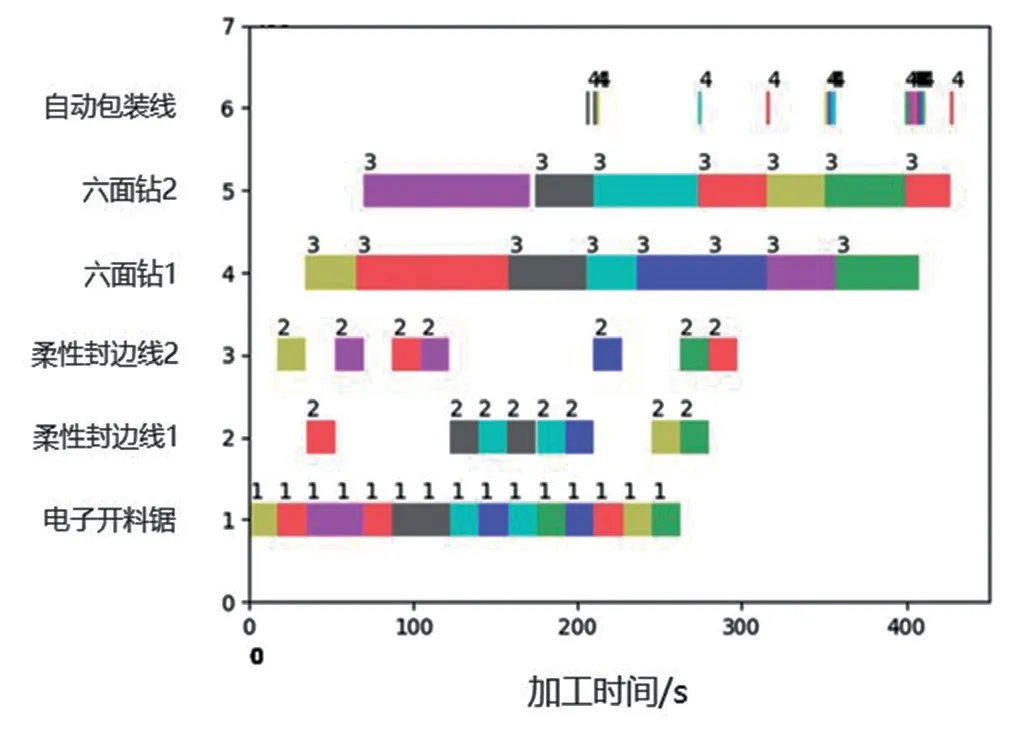
其中，遗传算法迭代结果最好的一次进化过程即上述第5次迭代结果如图3所示，横坐标代表迭代次数，纵坐标代表每代个体即加工板件的完工时间。由图可知，目标函数随着种群的进化而逐渐减小，进化到315代左右后，基本收敛于极值。同时，利用python软件生成了板式定制家具带相同并行机混合流水车间调度的甘特图（图4），图中可以看出各板件在各工序上的加工顺序以及设备分配情况。

■图3 遗传算法进化曲线图

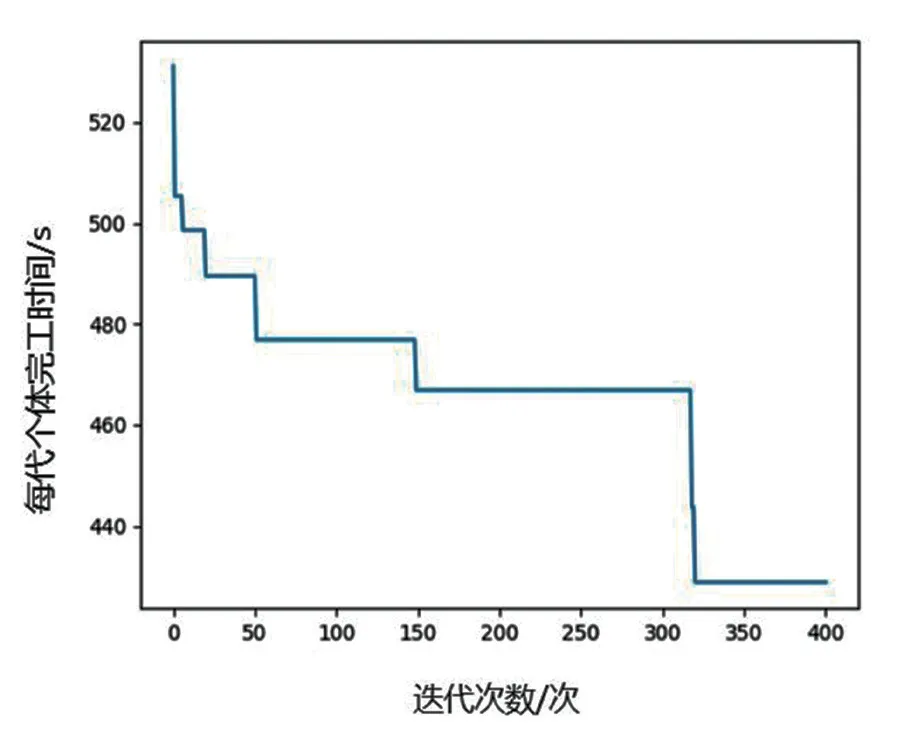
■图4 混合流水车间调度甘特图

通过以上仿真数据可知，本例的最小化最大总完工时间为428.8秒，各板件具体的加工顺序和设备分配情况如表3所示，1-60表示所有板件开始加工时的时间节点排序情况，例如14表示在此次生产调度中，板件5的封边工序是在第1台柔性封边线上进行加工的，它在所有板件全部工序的调度顺序中是14。而在车间实际的生产当中，完成这十五块板件的总加工时间为465.8秒，总加工时间减少了37秒，生产效率提升了8.6%，缩短了产品的总完工时间。上述的混合流水车间调度问题只针对15块板件进行了计算，在实际生产中会有更多的板件，此时只需要在代码中增加不同板件的加工时间，即可实现更大数量板件的相同并行机混合流水车间调度。