基于同步压缩和DCGAN的癫痫脑电信号检测方法*

齐永锋,裴晓旭,吕雪超,王 静

(西北师范大学计算机科学与工程学院，甘肃 兰州 730070)

1 引言

癫痫是一种慢性神经系统疾病，这种疾病会扰乱大脑神经元的正常活动，发作时患者可能会出现受伤甚至危及生命的紧急情况，给患者带来了极大的心理压力与工作生活困难[1]。因此，迫切需要一种实用可靠的自动化技术来实现准确预测癫痫发作。在癫痫发作出现临床症状之前，最常见的推断方法是分析脑电信号EEG(ElectroEncephaloGram)。EEG是一种无创、多通道的脑电活动记录。由于包含了很多病理信息，脑电信号中的某些特征通常被用于一些脑部疾病的临床诊断，特别是对于癫痫患者的观察和治疗，其作用是其他检测方法无法替代的[2]。

在过去的几十年中，关于癫痫识别和预测的研究方法很多，传统的方法一般需要人工设计算法来获取脑电信号特征，然后与机器学习相关分类器相结合实现癫痫信号的自动识别。提取信号特征的方法通常包括时域、频域和时频域3种，如利用小波变换、形态学分析等方法提取样本特征，然后通过随机森林、最近邻和支持向量机等方法对样本进行分类。Hwang等[3]提出基于短时傅里叶变换FTST(Short-Time Fourier Transform)的脑电信号时频域分析方法,在处理分段平稳信号或近似平稳信号时达到了较好的频率分辨率。然而对于非平稳信号，利用该方法获得的频谱图中存在能量不集中的现象，故而难以进一步提取EEG特征。2011年Daubechies等[4]提出了一种同步压缩变换SST(SynchroSqueezing Transform)的时频域处理方法，该方法首先计算时频谱的瞬时频率，在频谱图中以频率方向将能量重新分布，使得最后获得的频率曲线更加精准，极大地提高了时频可读性[5]。2014年，Oberlin等[6]提出以短时傅里叶变换为基础的傅里叶同步压缩变换FSST(Fourier-based SynchroSqueezing Transform)，通过对信号进行STFT变换获取信号瞬时频率，经过同步压缩处理后锐化了脑电数据频谱图像，改善信号时频曲线交叉现象，同时FSST也支持信号重构。同步压缩变换的提出为癫痫脑电信号的处理提供了新的思路[7]。

目前的各类深度学习网络模型已经能够理解和识别一般的自然图像，尤其是卷积神经网络CNN(Convolutional Neural Network)不需要人工提取就能够自动学习图像特征，已成功应用于许多领域中。CNN虽然对图像的特征提取和学习能力较强，但用于癫痫脑电分析时仍需要大量的癫痫脑电训练数据，并且由于复杂度过高、数据分类不平衡导致其性能不稳定，样本量太少导致其识别能力差。Goodfellow等[8]于2014年提出了生成式对抗网络GAN(Generative Adversarial Network)，该网络通过对抗博弈训练来模拟生成模型，通常将原始图像和随机噪声共同作为输入，以对抗学习的方式进行训练，不断估计数据样本的潜在分布，同时自动生成靠近真实数据的样本，缓解了带标签的癫痫脑电数据严重不足的问题。然而，GAN网络的不稳定性也会导致输出不理想、性能不稳定及系统崩溃等问题的产生。Radford等[9]针对上述问题，提出了深度卷积对抗生成网络DCGAN(Deep Convolutional GAN)。通过把有监督学习的CNN模型和无监督学习的GAN结合在一起，在生成对抗网络模型中引入卷积运算进行无监督训练，卷积神经网络的特征提取优势有效提升了生成对抗网络的学习能力。

为了更准确地检测癫痫发作，本文把 FSST 方法和DCGAN引入到癫痫发作预测任务中，提出基于同步压缩短时傅里叶变换FSST和深度卷积生成对抗网络DCGAN的癫痫脑电信号检测方法。本文工作主要包括以下内容：(1)针对短时傅里叶变换对脑电信号数据进行处理时存在的问题，加入了同步压缩方法，以获得更精确的频率曲线，明显提高了EEG信噪比和信号提取精度；(2)为了有效解决癫痫脑电信号样本量不足、特征提取手段较为单一的问题，构建了深度卷积生成对抗网络用作特征提取器；(3)对获取的脑电信号特征进行分类识别和标记，实现癫痫发作预测。在CHB-MIT头皮脑电数据集上进行仿真分析与实验验证。实验结果表明，所提方法具有较高的分类精度，可达到97.9%。生成对抗网络作为一种无监督学习技术，可有效解决样本量不足的问题，结合同步压缩变换预处理方法后取得了良好的实验结果，具有良好的癫痫脑电信号检测性能和临床应用潜力。

2 方法理论与模型

2.1 傅里叶同步压缩变换

短时傅里叶变换STFT方法是一种常用的信号时频域分析法。相比傅里叶变换多了加窗平滑处理的过程，先加窗再进行傅里叶变换，将信号视为短时平稳信号的不断拼接，得到不同时刻的频谱，对于非平稳信号具有较好的处理能力。首先利用STFT对信号s(t)进行处理，如式(1)所示：

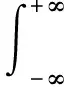
(1)

其中,g(·)为窗函数。Gs(ω,t)定义为STFT的频谱图。信号在位于t处的短时傅里叶变换等于信号与该时刻处的窗函数g(u-t)傅里叶变换之积。简而言之，短时傅里叶变换的思想是首先确定固定的窗函数，假定信号在窗内是平衡的，采用傅里叶变换分析窗内信号，通过移动窗函数，得到信号频率随时间的变化关系，从而确定输入信号局部区域的频率谱。由于STFT采用固定的窗函数，分辨率也被确定下来，当信号变化剧烈或者变化较为平缓时，STFT无法同时兼顾时间和频率上的分辨率要求[10]，因此不能达到最优。

而同步压缩变换(SST)能够将信号进行分解，使得信号具有时变振荡特性。通过计算时频谱的瞬时频率，将图中的能量以频率方向进行压缩,提高时频的可读性[11]。

Gs(ω,t)相位不受时间窗长度的影响，利用其相位来计算瞬时频率vG(ω,t)，若Gs(ω,t)不等于0，则能够得到时频谱中每一个时频点的瞬时频率,如式(2)所示：

(2)

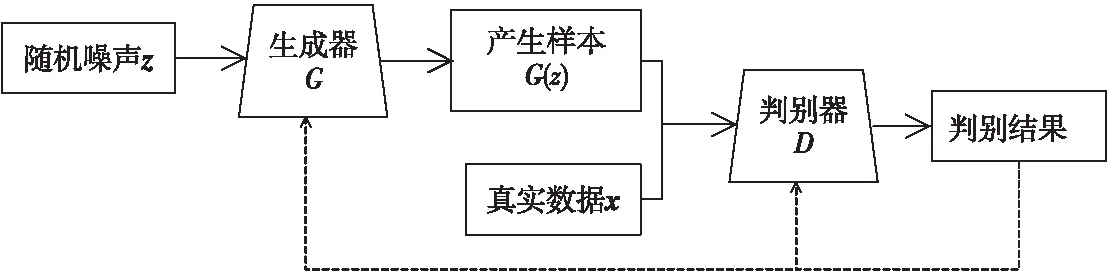
Figure 3 Process of generative adversarial networks

通过式(2)计算得到瞬时频率，通过映射(t,ω)→(t,vG(ω,t))在时频平面内对初步的时频分布沿着频率方向进行重新分配，时频重排可以表示为式(3)：

(3)

其中,δ(·)为单位脉冲函数。

同步压缩SST在频率方向对STFT的结果进行压缩。作为一种后处理工具，SST能够达到提升时频谱能量聚集的目的[12]，还可以重构信号，从而提高了最终识别正确率。

图1为原始脑电信号图。信号经过同步压缩变换处理后得到的时频图像如图2所示，从图2可以看出，在相应的时间和频率下能量不同。由图2可知，经过FSST变换后得到的频率谱能量聚集性较高，频率曲线明显。

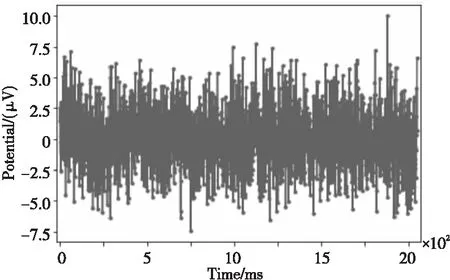
Figure 1 Original EEG

Figure 2 Time-frequency image after preprocessing

2.2 深度卷积生成对抗网络

生成对抗网络GAN是一种深度学习模型，最早由Goodfellow于2014年提出，主要由2部分结构组成：生成器G和判别器D。G和D是一种博弈对抗关系，在博弈过程中生成器生成的伪样本慢慢接近真实数据，判别器的判断能力逐渐增强，最终达到一种动态平衡[13,14]。该过程可以用式(4)表示：

Ez～Pz(z)[log(1-D(G(z)))]

(4)

其中,x为真实数据，服从真实数据分布Pdata(x)；z为随机噪声，服从先验分布Pz(z)；G(z)是将随机噪声z输入到生成器所产生的伪样本；D(x)和D(G(z))分别为判别器判断x和G(z)为“真”的概率。生成对抗网络工作过程如图3所示。

Radford等[15]提出了结合卷积神经网络和生成对抗网络的深度卷积生成对抗网络DCGAN模型。针对DCGAN存在的一些问题，如网络训练难以收敛、生成样本质量不高等，本文在深度卷积生成对抗网络基础上进行以下改进：在每一个卷积层中增加批标准化BN(Batch Normalization)来优化网络模型，使其更好地学习数据特征；用卷积层替代池化层，使生成对抗网络训练CNN时更加稳定。DCGAN以无监督的方式进行训练，训练生成的判别器可以用于图像的特征提取。

本文使用的深度卷积生成对抗网络中的生成器结构如图4所示。生成器从随机噪声中获取100维样本作为输入。输入端与输出大小为6 272的隐藏层完全连接，然后将其整形为64×7×14。隐藏层之后是3个反卷积层，卷积核大小为5×5，步长为2×2。3个反卷积层的卷积核数目分别为32,16和16。生成器的输出与脑电信号预处理后的频谱图像具有相同的维数。

Figure 4 Structure of generator

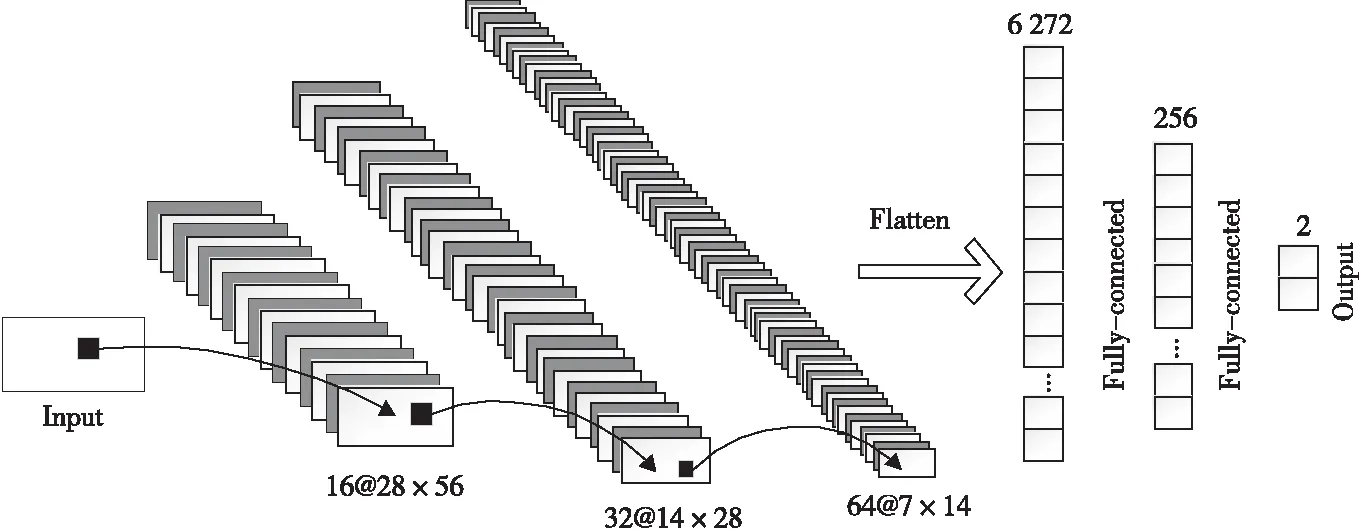
Figure 5 Structure of discriminator

另一方面,判别器将生成的EEG数据与真实数据区分开来，其结构如图5所示。输入EEG信号,经过同步压缩短时傅里叶变换预处理,生成频谱图，输入样本数据维度为56×112。之后由3个卷积层提取特征，卷积核大小为5×5，步长为2×2，3个卷积层的卷积核数目分别为16,32和64。提取的特征被展平输入到2个全连接层中，输出维度分别为256和2。

3 实验与结果分析

3.1 数据集

本文实验数据来自由波士顿儿童医院CHB(Children’s Hospital Boston)和麻省理工学院MIT(Massachusetts Institute of Technology)共同创建的头皮脑电信号开源数据集。该数据集为全球提供大量可免费公开访问的生理信号数据。CHB-MIT数据集包含23名年龄在3～22岁的癫痫患者的头皮脑电数据，其中男性5名，女性18名。数据集详细描述见文献[16]。

由于原始数据无法直接应用到具有3个卷积层的生成对抗网络结构中，所以需要先对原始数据进行预处理。使用同步压缩短时傅里叶变换方法将时间序列EEG信号转换成由频率轴和时间轴组成的二维矩阵。

不同患者的脑电记录的通道数量不全相同，如Pat4和Pat13 2位患者的脑电记录分别有20个和17个可用通道。为了便于数据合并和更有效地训练GAN,本文预处理按照文献[17]中的方法，在CHB-MIT数据集中为每个患者选择16个通道，使所有患者具有相同数量的通道。利用短时傅里叶变换，使用1 s长度和50%重叠的余弦窗口，对脑电信号进行时频分析。由于STFT会严重受到噪声影响，且得到的频谱图像分辨率不高，导致最后的分类效果不佳，故下一步通过同步压缩变换对STFT得到的时频平面能量在频率方向进行重新分配，对时频曲线进行压缩，以达到提高分辨率的目的。最后将时间序列EEG信号转换成由频率轴和时间轴组成的二维矩阵。

3.2 评估标准

为了准确评价本文提出的方法，利用Schelter等[18]提出的评价方法。由于目前关于癫痫发作预测方法均无法准确预测到癫痫发作的具体时刻，而是确定癫痫发作的一个时间范围，文献[18]定义了发作出现时期SOP(Seizure Occurrence Period)和发作预测范围SPH(Seizure Prediction Horizon)2个变量。其中,发作预测范围(SPH)指的是癫痫发作前的预测时间段，发作出现时期(SOP)指癫痫一定会发作的时间段。为了给出正确的预测，癫痫发作点必须在SPH之后且在SOP范围内。也就是说系统发出警报之后，在SPH内无癫痫发作，而在SOP内有一次发作被视为一次正确的预测，反之则为一次错误的预测。

在临床医疗应用中，SPH过短会影响对患者的治疗和干预，太长会造成患者和医护人员的心理压力，因此SPH也被称为干预时间。在本文实验中，SOP设置为30 min，SPH设置为5 min。癫痫发作的确切时间可能在SOP内有所不同，故预测存在一定的不确定性。

本文分别利用敏感性、特异性、准确率和假阳性率对癫痫脑电信号检测方法的性能进行评价。

(1)敏感性Sen(Sensitivity)，指检测系统对癫痫即将发病的敏感程度(识别能力)，计算如式(5)所示：

(5)

其中，NPS为正确识别癫痫发作前期的次数，NTN为癫痫发作前期总次数。

(2)特异性Spe(Specificity)，指检测系统对癫痫发作间期的特征识别能力,计算如式(6)所示：

(6)

其中，NCS为正确识别的发作间期的次数，NTS为发作间期的总次数[19]。

(3)准确率Acc(Accuracy)，评估测量系统分类性能的优劣,计算如式(7)所示：

(7)

(4)假阳性率FPR(False Positive Rate)，表示当前被错误分到癫痫发作前期类别中的样本所占比例,计算如式(8)所示：

(8)

3.3 实验结果

本文实验在Windows操作系统下进行，基于开源深度学习框架TensorFlow，使用编程语言Python实现。实验数据来自CHB-MIT脑电数据集中的23名患者的相关数据，采用十折交叉验证方法。

3.3.1 本文方法检测效果

本文基于SOP=30 min和SPH=5 min计算所有指标。通过CHB-MIT脑电数据集获得的癫痫发作预测结果。

表1详细描述了CHB-MIT数据集中各患者的信息及其识别准确率，包括患者性别、癫痫发作次数、持续时间和间隔时间等。本文方法对不同患者的检测结果各不相同，其中Chb07患者的识别准确率最高，为99.12%,23名患者的平均识别准确率达到了97.97%。

3.3.2 特征提取有效性分析

对于癫痫发作预测任务，最关键的部分是确定所有阳性病例，即错过癫痫发作前期但未被发现的患者脑电数据。此外，实验结果中错误警报的次数越少，方法性能越好。因此，对实验结果的评估主要基于灵敏度、FPR值及准确率。

本文比较了半监督学习模型FSST-DCGAN和完全监督模型CNN在CHB-MIT数据集上的检测效果，同时也将文献[20]中的方法在CHB-MIT数据集上进行了仿真实验，结果如表2所示。结果显示，在不同方法对不同患者的检测结果各不相同，这与数据特征有关，如癫痫发作次数和时间间隔等。FSST-DCGAN方法在该数据集上的平均敏感度高于表2中CNN和CNN仿真实验的结果，达到了89.06%;同时，对于患者Chb01,Chb02,Chb03,Chb09,Chb18,Chb21和Chb23来说，本文方法的FPR值为0，这说明本文方法相较于CNN模型对癫痫发作预测更加有效。

为进一步分析本文所提方法，将其与最近使用CHB-MIT数据集进行癫痫检测的方法进行比较，结果如表3所示。

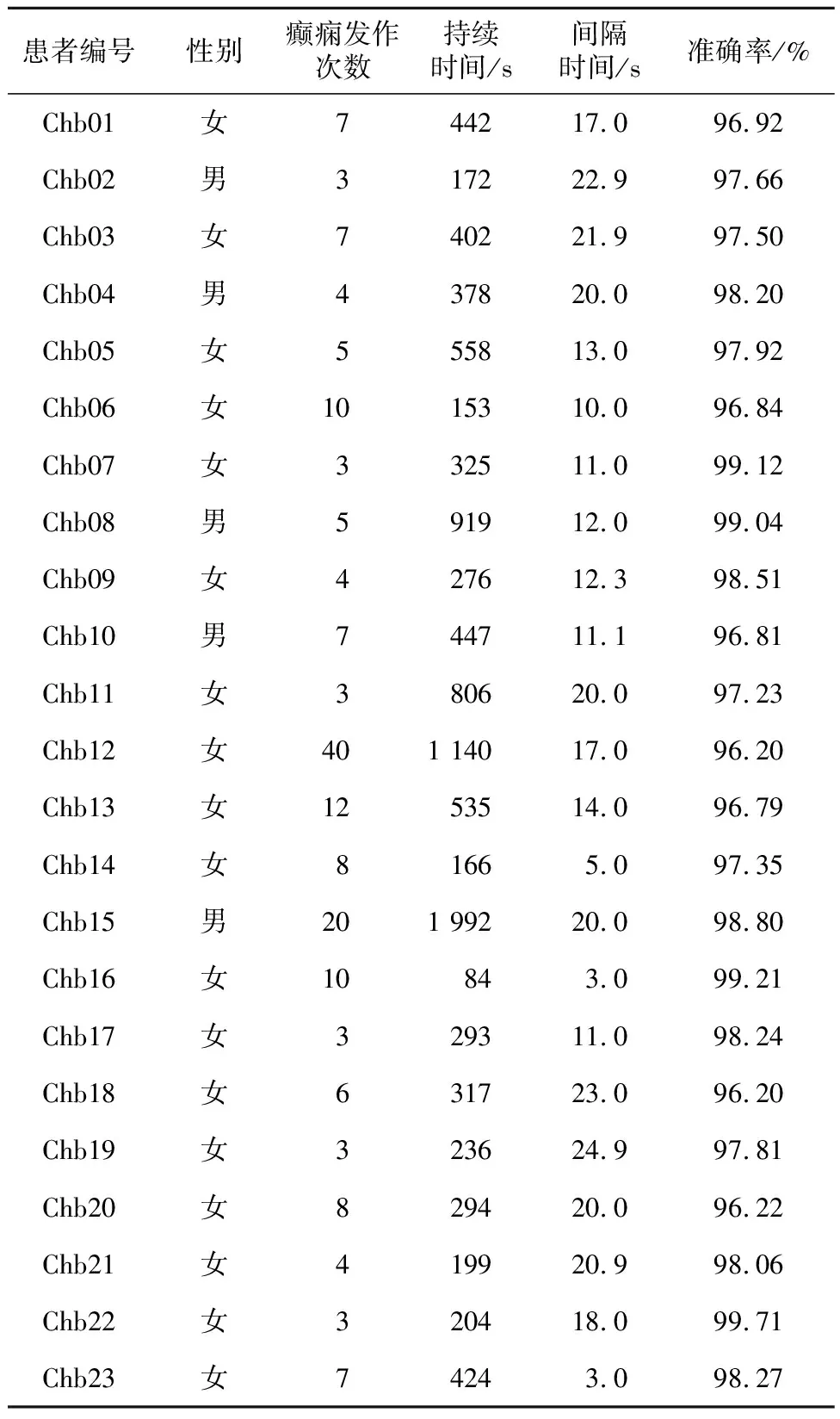
Table 1 Detection results of the proposed method

Table 2 Result comparison of CNN method and the proposed method

Table 3 Results comparison of different feature extraction methods

从表2和表3可以看出，本文方法与不同特征提取方法相比，识别准确率明显较高，但还存在需改进的地方，比如对于一些患者，FPR值较高，这也是以后需要研究分析的内容。

4 结束语

目前，国内外关于癫痫脑电信号检测的相关方法逐渐增多，虽然有些方法已取得较好的结果，但仍旧处于发展阶段，还有许多问题没有被完全解决。本文将FSST和DCGAN引入癫痫脑电信号检测中，提出了一种新的FSST-DCGAN模型来预测癫痫发作。在CHB-MIT数据集上评估了该方法的性能，实验结果表明，本文提出的FSST比传统的STFT更好，有效提高了脑电信号的提取精度。同时，使用深度卷积生成对抗网络进行特征提取，既减少了EEG昂贵又耗时的标记任务，又有效解决了样本量不足的问题。结合2种方法提取脑电信号数据特征的方法在癫痫预测任务中取得了较为理想的敏感性和准确率。通过对比其他特征提取方法，也验证了本文方法在癫痫脑电信号检测上的可行性和有效性。