采用双档案协同进化离散多目标烟花算法的低碳疫苗冷链优化配送*
2022-12-22申晓宁陈庆洲潘红丽
申晓宁,游 璇,陈庆洲,潘红丽,黄 遥
(1.南京信息工程大学自动化学院,江苏 南京 210044;2.江苏省大气环境与装备技术协同创新中心,江苏 南京 210044;3.江苏省大数据分析技术重点实验室,江苏 南京 210044)
1 引言
随着计划免疫和常态化防疫工作的深入开展,疫苗的需求量不断攀升,疫苗冷链物流成为现代物流中的一个重要分支[1]。因此,低碳疫苗冷链优化配送已成为亟需解决的一类实际物流应用问题。该问题对固定数量的配送车辆进行路径规划,它的成功求解,能使疫苗的冷链配送服务更有秩序、效率更高,及时满足各个地区的疫苗需求,提高当地的人民健康与医疗卫生服务水平,同时有效减少二氧化碳的排放量,改善周围大气环境。
目前,国内外研究人员已经分别对疫苗的运输策略和配送方式等进行了研究。de Carvalho等[2]提出了一个多目标、多周期的混合整数线性规划模型,用于可持续疫苗供应链的设计和规划,并以一家欧洲公司为典型案例进行了详细研究。基于包括分销商和零售商的疫苗供应链,Qi等[3]提出了一个基本模型研究分销商通过冷链或非冷链运输疫苗的条件和冷链运输的策略。郑浩[4]根据疫苗的保存条件、流通特征等,对长途和短途的疫苗冷链配送问题分别进行了详细的研究,提出了能够规避风险且降低成本的运输策略。陈勇等[5]建立了多品种疫苗的共同配送模型,有利于提升疫苗运输的时效性,并减少运输成本。郑春姣[6]以泰丰生物制品有限公司为例,分析现有疫苗冷链配送方案存在的不足,并从组织结构、配送方式和冷藏包装等方面对方案进行了改进,促进了公司在疫苗冷链业务上的发展。
烟花算法是由谭营等[7]在2010年首次提出的一种元启发式算法。它模拟烟花在夜空中爆炸的过程,将烟花爆炸产生的火花看作问题的一个解,将烟花爆炸产生多个火花的过程看作其搜索邻域的过程。目前,烟花算法已成功应用于复杂网络关键点集确定[8]、多区域电力系统调度[9]、电能交易[10]等多个实际问题的求解。本文提出一种双档案协同进化离散多目标烟花算法,简称DTAMOFWA(Discrete Two-Archive-based Multi-Objective FireWorks Algorithm)。通过仿真实验验证了改进策略的有效性,并将DTAMOFWA与4种已有算法进行对比,实验结果表明,所提算法在低碳疫苗冷链配送问题上具有更好的求解性能。
2 低碳疫苗冷链配送问题的数学模型
为了使疫苗在规定的客户(包括医院、各级疾控中心、诊所等)时间窗内尽快送达并产生较少的碳排放量,本文将低碳疫苗冷链配送问题建模为约束多目标优化模型,最小化运输成本和平均客户不满意度,同时考虑可用车数量约束、车辆容量约束和模糊时间窗约束[11]。
2.1 问题描述
低碳疫苗冷链配送问题的描述如下:存在1个配送中心(编号为0)和n个客户(编号为1~n),由一定数量的同类型配送车辆对各个客户进行配送服务,目标是在满足约束的条件下使运输的总成本和客户不满意度尽可能地小。配送方案需满足客户对疫苗需求量和模糊时间窗的要求,每个子回路中所有客户的需求量之和不超出配送车辆的容量限制,且实际配送车辆数不超过配送中心可用车辆数。每辆车从配送中心出发和回到配送中心时均需进行一定时间的消毒。配送车辆在疫苗配送过程中每间隔一定时间需对制冷设备添加一次制冷剂。
2.2 符号和变量
低碳疫苗冷链配送问题数学模型中的符号和变量含义如下所示:
n:客户数量;
K:可用车辆数;
Q:运输车辆的最大容量(t);
w:运输车辆的自身重量(t);
qi:客户i的需求量(t);
dij:从客户i处到客户j处的车辆行驶距离(km);
lij:从客户i处行驶到客户j处时的车辆载重(t);
vij:从客户i处到客户j处的车辆行驶速度(km/h);
Ce:碳税(元/吨);
FE:燃油排放参数(t/L);
a:车辆行驶加速度(m/s2);
g:重力加速度常量(m/s2);
θij:从客户i处到客户j处这一路段的路面坡度;
Cr:滚动阻力系数;
Cd:牵引力系数;
A:车辆正面表面积(m2);
ρ:空气密度(kg/m3);
P1:单位货物在行驶单位距离时制冷产生的碳排放量(t/km);
P2:每小时司机的薪酬(元/小时);
tdis:车辆在配送中心的消毒时间(h);
tsi:车辆在客户i处的服务时间(h);
P3:制冷剂单价(元);
T:添加制冷剂的间隔时间(h);
[ETi,LTi]:客户i可接受的时间窗;
[ETi′,LTi′]:客户i期望的时间窗;
ti:车辆到达客户i的时刻;
t0:车辆的出发时刻;
U0:疫苗在出发时的品质;
σ:疫苗品质的衰减指数。
2.3 数学模型
低碳疫苗冷链配送问题的数学模型中,定义决策变量如式(1)和式(2)所示:
(1)
(2)
目标函数和约束条件如式(3)~式(12)所示:
minZ1=C11+C12+C2+C3=
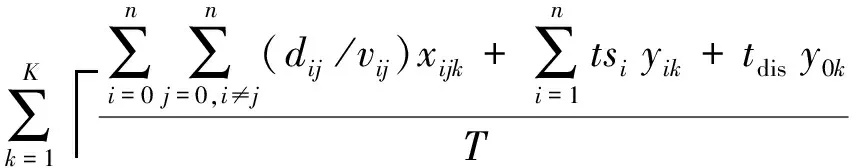
(3)
(4)
(5)
其中,式(3)表示运输成本目标函数,包括油耗碳排放成本C11、制冷碳排放成本C12、司机薪酬C2和制冷剂成本C3。采用一种综合的碳排放计量模型,同时考虑行驶距离、速度等多种因素对车辆耗油量的影响,通过燃油排放参数与耗油量的乘积获得车辆在该路段行驶产生的碳排放量[12]。式(4)表示平均客户不满意度目标函数,包括平均时间不满意度和平均品质损失程度。式(5)为车辆到达客户i处时的时间满意度。式(6)~(12)为约束条件,式(6)表示每个客户只能由一辆车服务;式(7)和式(8)表示对于每个被服务的客户点,一定会有一辆车从某个地点行驶到该客户点,并从该客户点离开;式(9)为经典的子回路消除约束,保证每辆车的行驶路线中没有子回路;式(10)为车辆容量约束;式(11)为车辆数量约束;式(12)为模糊时间窗约束。
3 双档案协同进化的离散多目标烟花算法DTAMOFWA
针对低碳疫苗冷链配送问题数学模型的特点,本文提出双档案协同进化的离散多目标烟花算法DTAMOFWA,设计了消除车辆数量和容量约束的解码方式、部分映射爆炸算子和双外部档案协同进化机制,以提高算法的求解性能。
3.1 个体编码和消除车辆约束的解码方式
DTAMOFWA采用整数编码,对于包含n个客户(编号为1~n)的问题,每个个体的编码均为一串整数序列,其中每个整数的取值在1~n。由于低碳疫苗冷链配送问题带有较多强约束条件,导致搜索过程中容易产生大量不可行解,不利于最优配送方案的求解。因此,在DTAMOFWA中设计了一种消除车辆数量和容量约束的解码方式。首先,对整数编码序列按车辆容量约束和模糊时间窗约束进行解码,即从配送中心出发,依次访问编码中的各个客户。若某客户违反上述2个约束中的任一个,则该子回路结束,并将违反约束的客户作为下一个新子回路的第1个访问对象,直到所有的客户均被访问,解码结束。此后,判断子回路数量,即使用的车辆数是否超过问题可用车辆数,若不超过,则所得解为可行解;若超过,则对原整数编码个体仅按车辆容量约束重新解码,并采用一种新型修复算子,使得已经满足车辆容量约束的序列进一步满足车辆数量约束,从而得到仅违反模糊时间窗约束的解。
该修复算子对客户访问序列按车辆容量约束解码后,当子回路数量达到可用车辆数时,将剩余未访问的所有客户放入一个集合中。对该集合依次进行插入操作和置换操作,删除满足特定条件的客户编号。若集合变为空集,则该修复操作终止;若集合无法变为空集,即经插入和置换操作后,仍不能同时满足车辆数量和容量约束,则随机初始化一串访问序列替代原整数编码个体,并重新解码。插入操作是指:依次判断集合中每个编号是否能在不违反车辆容量约束的前提下插入某个已有子回路。若能,则将该编号插入已有子回路中并将其从集合中删除;若不能,则保留在集合中等待进行置换操作。置换操作是指:对集合中的每个编号,在不违反车辆容量约束的前提下将其与每个子回路最小客户需求量对应的编号进行置换。若置换成功,则对当前集合进行插入操作;若置换失败,则将该编号继续留在集合中。以客户数量为8,可用车辆数为3,车辆最大容量为12为例,2种操作如图1所示。图1中,qi表示客户i的需求量,Y1为执行操作前的解,0为配送中心的编号,子回路分别为k1,k2,k3和k4,Y′1为执行操作后所得解。
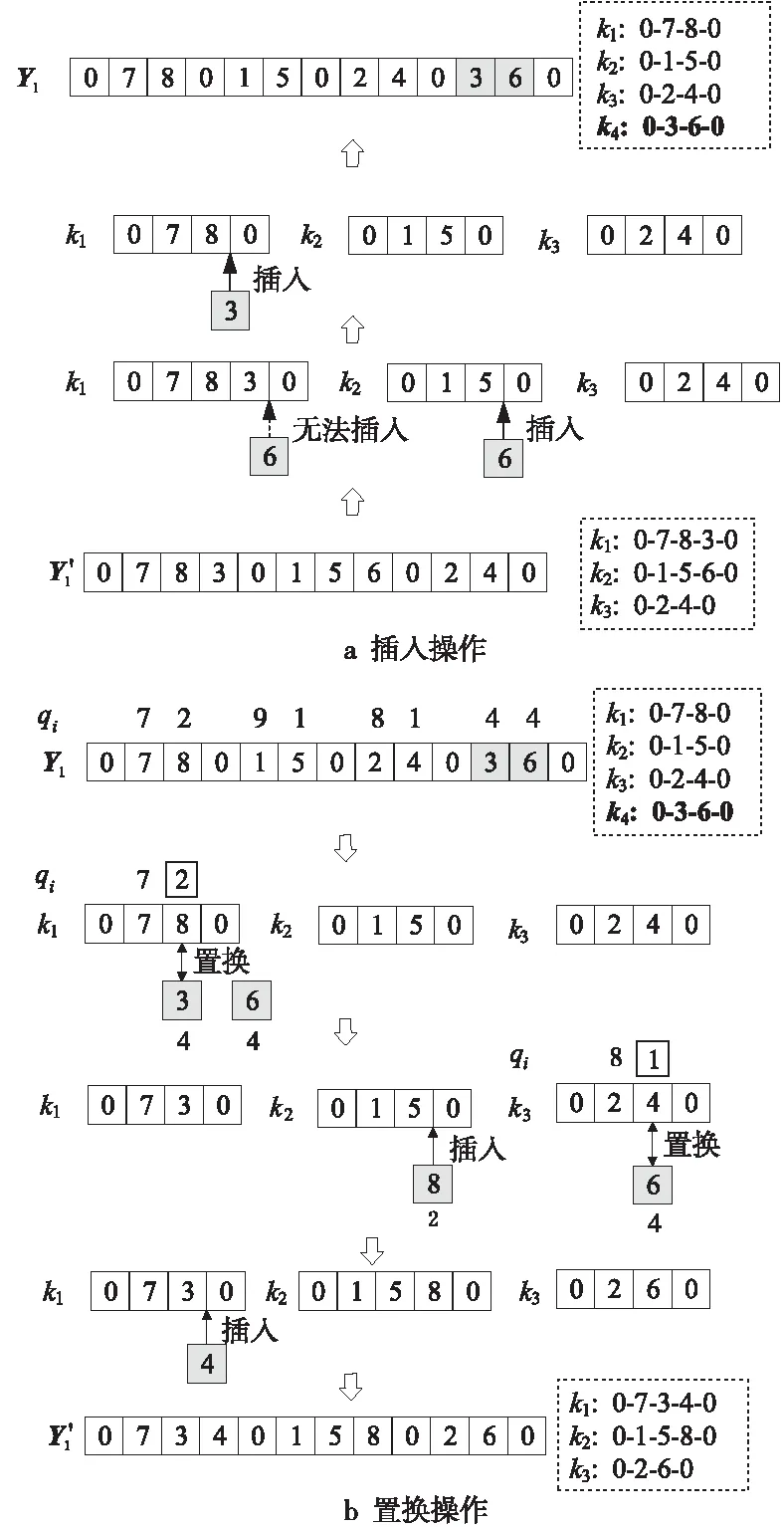
Figure 1 Repair operator for eliminating vehicle quantity constraint and vehicle capacity constraint
本文所提解码方式能有效消除车辆数量和容量约束,生成解大部分为可行解,少数不可行解也可通过修复算子将其转化成只违反模糊时间窗约束的解。该操作大大增加了寻优过程中可行解的获取数量,降低了因不可行解数量大而为搜索带来的难度。同时,算法仅需对模糊时间窗约束进行处理,提高了算法的搜索效率。
3.2 部分映射爆炸算子
由于低碳疫苗配送问题属于组合优化问题,原来求解连续优化问题的爆炸算子在本文中并不适用。为了使产生的爆炸火花更均匀地分布在以烟花为圆心、一定幅度为半径的圆形区域内,充分利用有限的计算资源进行搜索,本文设计了部分映射爆炸算子,考虑通过个体编码中发生变化的编号个数,来表示决策空间中在烟花周围产生的位移大小。该算子采用新的爆炸半径计算公式,并融合部分映射交叉操作生成固定数量的爆炸火花。部分映射交叉所选取的编码片段长度由所计算的爆炸半径决定。
假设烟花种群大小为N,问题决策变量维数为n,目标个数为m。所提爆炸算子计算第i个烟花Xi的爆炸半径的方法如下:首先将Xi的m个目标值分别进行归一化并相乘,得到乘积M(Xi),如式(13)所示;其后,再将M(Xi)归一化的结果与决策变量维数n相乘,以确定Xi的爆炸半径Ai,即Xi需要发生爆炸的决策变量个数即客户点个数,如式(14)所示:
(13)
i=1,2,…,N
(14)
其中,fs(Xi)、fsmax和fsmin分别表示烟花Xi的第s个目标值、当前种群中所有N个烟花在第s个目标上的最大值和最小值;M(Xi)为各目标归一化后结果的乘积;Mmax和Mmin为当前种群中所有N个烟花对应乘积中的最大值和最小值;[·]表示四舍五入取整操作。根据式(14)计算烟花的爆炸半径,当某个烟花靠近一个极端解,即某一目标值很小时,归一化后的乘积较小,因此得到的爆炸半径也较小;当2个目标值都较大时,归一化后的乘积较大,因此得到的爆炸半径也较大;当2个目标值均比较折衷时,此时烟花在目标空间上处于当前Pareto前沿的中间位置。若该烟花更靠近坐标原点,说明其更接近真实Pareto最优前沿(最小化问题),归一化后的乘积较小,得到的爆炸半径较小;若该烟花离最优前沿较远,则归一化后的乘积与前一种情况相比较大,得到的爆炸半径相对较大。根据上述原理,所提爆炸半径计算公式能够合理地控制不同适应度烟花的爆炸半径,使得适应度较好的烟花实现较小范围的精细搜索,适应度较差的烟花实现较大范围的搜索。
令每个烟花产生4种爆炸半径的爆炸火花,其爆炸半径如式(15)所示:
(15)
每个爆炸火花的爆炸半径确定后,对每个烟花,将编码中的配送中心0删除,得到一串客户的访问序列。随机选取4个其它烟花的客户访问序列,分别与当前烟花进行部分映射交叉操作。ri1,ri2,ri3和ri4分别为每次交叉所选取的片段长度,交叉后按各自原配送中心位置解码可得到2个爆炸火花。以客户数量为8的序列为例,设爆炸半径即交叉选取的片段长度为4,则部分映射爆炸算子的操作过程如图2所示。X1和X2为2个烟花个体;子回路为k1,k2和k3;B1和B2为X1和X2的客户访问序列。B′1和B′2为将部分片段交叉后得到的客户访问序列。此时,B′1未交叉的部分与已交叉部分有重复的客户点,B′2也是如此。根据图2中的映射关系,将B′1和B′2未交叉部分的重复客户点分别进行替换,得到2个没有重复客户点的客户访问序列S1和S2,最后按X1和X2的配送中心位置解码得到2个爆炸火花E1和E2。

Figure 2 Partial mapping explosion operator
所提部分映射爆炸算子通过控制烟花的爆炸半径,交换烟花个体中不同长度的片段,使得个体之间能够进行不同程度的信息交流,让烟花根据自身特点在范围不同的区域内进行搜索,从而实现了算法在局部寻优和全局寻优之间的平衡。但是,由于该算子只对客户访问序列进行操作,配送中心的位置保持不变,限制了种群的多样性。
3.3 双外部档案协同进化机制
一些已有的多目标优化算法中处理约束的方法是直接将搜索过程产生的不可行解淘汰,只对可行解进行操作。但是,该方法不仅会丢失不可行解中的有用信息,且还可能导致种群同化现象严重。另外,在约束优化问题中,在可行域边界的不可行解约束违反程度较小,若在其附近进行局部搜索,则易于得到大量可行解。为解决上述问题,本文采用可行解档案和不可行解档案协同进化机制,如图3所示。DTAMOFWA设置了可行解档案和不可行解档案2个不重叠的外部档案,分别保存可行解和不可行解中的精英个体。
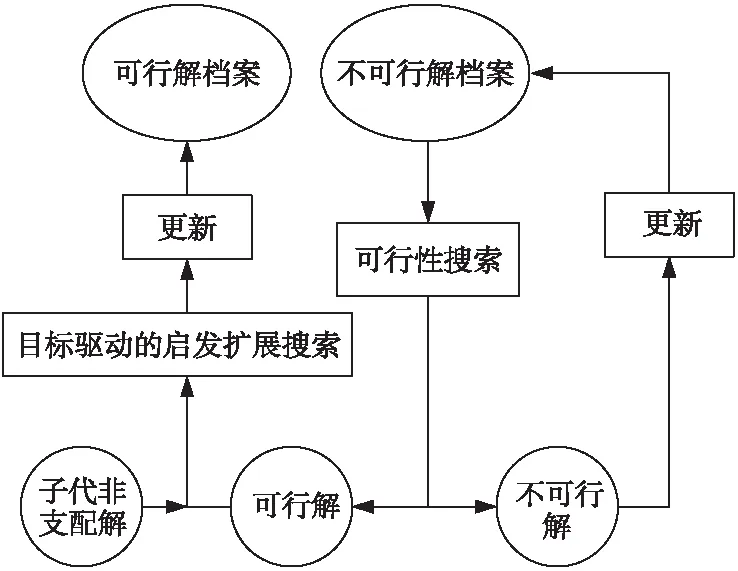
Figure 3 Schematic diagram of the coevolutionary mechanism of two external archives
对不可行解档案实施可行性搜索,可能生成新的可行解和不可行解。为了避免对同一个不可行解进行重复搜索,若不可行解档案中的个体数量大于烟花种群规模N,则每次从不可行解档案中随机选择N个个体进行可行性搜索;否则,对不可行解档案中的所有个体进行可行性搜索。按照3.1节消除车辆数量和容量约束的解码方式进行解码,种群中的不可行解均只违反模糊时间窗约束。因此,可行性搜索策略对某个配送方案中违反时间窗约束程度最大的子回路,按客户可接受到达时间进行排序,所得的新配送方案称为可行性搜索火花。为了防止产生的新解相似度过高,导致出现早熟收敛的情况,所提可行性搜索策略每次仅对违反约束程度最大的一个子回路进行调整。以客户数量为8,车辆数为3的序列为例,可行性搜索如图4所示。其中,k1为违反时间窗约束程度最大的子回路。编号下方的时间为客户的可接受到达时间,优先选择可接受到达时间早的客户,以降低不可行解的约束违反程度。
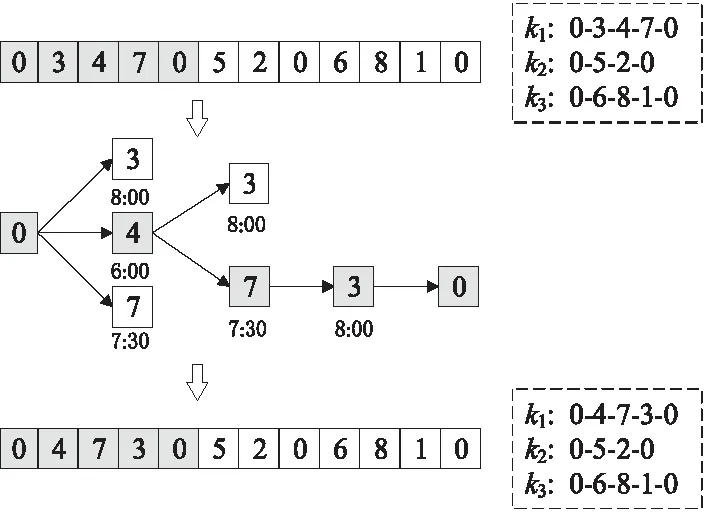
Figure 4 Feasibility search strategy
对于不可行解档案经可行性搜索后产生的可行解,将其与子代中的非支配个体共同进行目标驱动的启发式扩展搜索。该搜索操作利用问题目标中包含的启发信息——碳排放量和客户不满意度,将个体中碳排放和客户不满意度最大的子回路的客户编号重新排序。排序时依次选择碳排放量或客户不满意度最小的路段终点编号作为下一个访问客户。经过该操作后,用所得解更新可行解档案,使其在可行空间不断向Pareto最优前沿进化。此外,利用可行性搜索产生的不可行解,根据时间窗约束违反程度更新不可行解档案,使其在约束空间向可行区域不断移动,达到2个外部档案协同进化的效果。若不可行解档案规模超过预设外部档案的最大规模,依次选取其中约束违反程度最小的解进入不可行解档案;否则,不可行解档案保持不变。
采用双外部档案协同进化机制,能够充分利用不可行解中的有用信息不断推进搜索进程,提高搜索效率。此外,由于可行性搜索没有对子回路中的客户进行增删操作,因此得到的新配送方案依然不违反车辆的容量和数量约束。
3.4 算法的求解步骤
步骤1初始化。对问题模型及算法中的变量和相关参数进行初始化设置。均匀随机生成规模为N的烟花种群POP(POPulation),根据消除车辆约束的解码方式进行解码,并计算其目标向量。将POP中的可行解加入可行档案Feasible,不可行解加入不可行解档案Infeasible。设置当前目标评价次数Eva=N,最大目标评价次数为Evamax。
步骤2部分映射爆炸算子。每个烟花根据4种不同的爆炸半径通过部分映射交叉操作产生8个爆炸火花。更新Eva=Eva+ 8*N。
步骤3变异算子。对每个烟花编码进行随机的两点交换操作。更新Eva=Eva+N。
步骤4将爆炸火花和变异火花中的非支配解加入NDS(Non-Dominated Set),并将其中的不可行解加入Infeasible。
步骤5对Infeasible进行可行性搜索,得到可行性搜索火花,其中可行解集为F,不可行解集为I,将Infeasible更新为I。更新Eva=Eva+N。
步骤6对NDS和F的并集实施目标驱动的启发式扩展搜索,得到扩展搜索火花SS(Search Sparks)。更新Eva=Eva+ 2*|NDS|。
步骤7更新种群。分别根据Pareto支配概念和ε支配概念[13],用NDS和SS的并集更新POP和Feasible。若规模超出最大预设值,则根据拥挤距离对POP和Feasible进行裁剪。使用I更新Infeasible。
步骤8选择策略。从POP和Feasible中各随机选择N/2个个体,若Feasible中个体数量小于N/2,则用POP中的个体补充。在选出的烟花种群中随机选择一个个体,计算该个体与其他烟花的相似度,即个体编码中对应位置编号相同的位置个数。将相似度高于80%的个体进行随机长度的循环移位操作。
步骤9终止条件。若Eva≤Evamax,则转移到步骤2;否则循环结束,输出Feasible。
4 仿真实验与结果分析
本文所有实验均在Intel(R)Core(TM)i5-10210U CPU@1.60 GHz,运行内存为12 GB的计算机上采用Matlab R2019a软件运行。根据对实际疫苗冷链配送过程的调研,生成不同规模的4个仿真实例,以验证3种改进策略的有效性和所提算法DTAMOFWA的整体性能。所有对比算法均在仿真实例上分别进行30次独立实验,每次实验的最大目标函数评价次数Evamax为50 000。实验中采用反世代距离IGD(Inverted Generational Distance)[14]和超体积HV(HyperVolume)[15]作为综合性能评价指标,对于计算HV时所需的参考点获取方式如下:将所有算法求得的非支配解在各目标上的最差值(最小化问题为最大值,最大化问题为最小值)分别放大1.5倍。将所有算法运行30次所得的全部非支配解合并成一个新的解集,再从该解集中确定出所有的Pareto非支配解作为该问题的近似Pareto最优解集。DTAMOFWA的种群规模N设置为10,可行解档案和不可行解档案的最大规模设置为100。
4.1 仿真实例的生成
本文低碳疫苗冷链配送问题是一个实际场景中的应用问题,由于无法获取到实际工程数据,因此根据对相关领域的调研,在一定参数范围内随机生成了4个不同规模的仿真实例,分别记为C-n15-k6、C-n20-k8、C-n35-k15和C-n55-k23。其中可用车辆数的估算方式如式(16)所示[16]。

(16)
其中,μ表示配送任务难度,实验中设置μ=0.5;车辆的最大容量Q=15 t。各仿真实例中客户位置的横纵坐标均在[0,200]内随机产生,配送中心的坐标为[100,100]。在[1,5]的整数范围内随机生成每个客户的需求量,并设置相应的时间窗限制和服务时间。构造一个(n+1)维的方阵表示编号为0~n的地点中任意两点间路段的行驶速度,速度大小均在[30,50]均匀随机生成,单位为km/h。低碳疫苗冷链配送问题模型中的参数设置如表1所示[17,18]。
4.2 改进策略的有效性验证
针对应用问题的特点,本文共提出了3种改进策略。为了验证改进策略的有效性,分别改变DTAMOFWA的相应策略,得到3种对比算法。首先,将相邻配送中心之间的编码作为一个子回路,用这种解码方式替换本文所提消除车辆约束的解码方式,得到对比算法DTAMOFWA-D。其次,将DTAMOFWA的部分映射爆炸算子替换为已有离散烟花算法DMOFWA[19]的爆炸算子,得到对比算法DTAMOFWA-E。最后,在算法搜索过程中直接淘汰所有不可行解,只对可行解进行操作,得到对比算法DTAMOFWA-V。所有算法的种群规模N均设为10。实验结果如表2所示,表中mean和std分别表示评价指标的平均值和标准差,每组数据的最佳值加粗表示;“+”“-”“=”为显著性水平为0.05的Wilcoxon秩和检验结果,分别表示本文算法显著优于、劣于对比算法以及与对比算法没有显著差别。
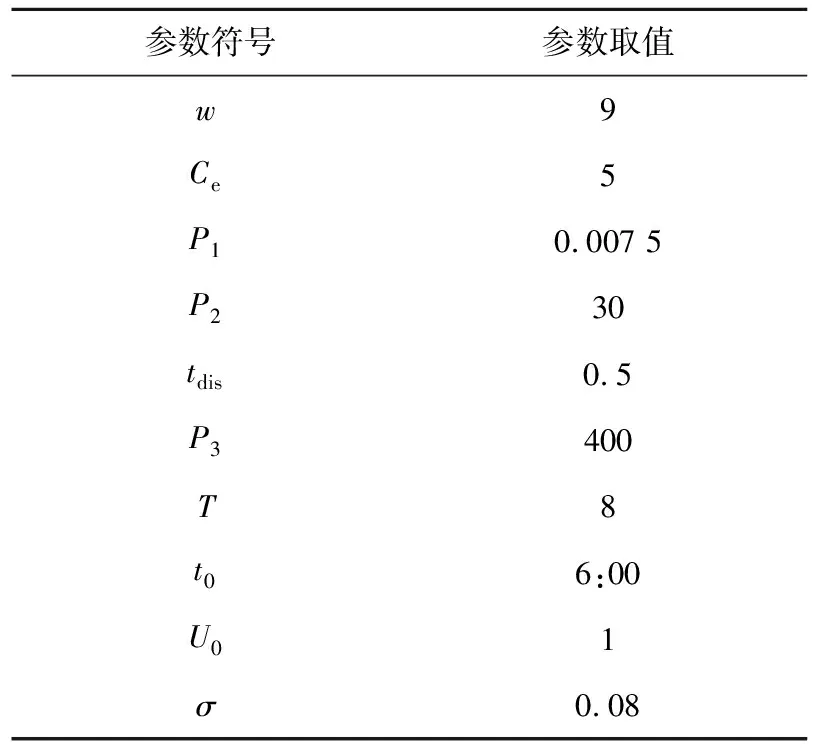
Table 1 Parameter settings in the model of low-carbon cold chain distribution of vaccines
由表2可知,DTAMOFWA在4个仿真实例上的IGD和HV平均值均为最佳;在C-n15-k6和C-n20-k8上的IGD标准差最优;同时在C-n20-k8上的HV标准差最优;在剩余实例上IGD和HV标准差与最优值也十分接近。Wilcoxon秩和检验结果也显示DTAMOFWA在IGD和HV上均显著优于其它对比算法。由此表明3种改进策略均是可行且有效的,都能在一定程度上提高DTAMOFWA的收敛性和多样性。DTAMOFWA的解码方式能够消除车辆约束,使得解码后的解大部分为可行解或仅违反时间窗约束的解,避免了大量不可行解对搜索进程的干扰。部分映射爆炸算子能够增强对局部区域的搜索,更好地实现全局搜索和局部搜索之间的平衡,提高了算法的求解精度。DTAMOFWA采用双外部档案协同进化机制,保留寻优过程中产生的约束违反程度较小的不可行解。利用可行性搜索产生的可行解辅助可行解档案进行寻优,同时利用可行性搜索产生的不可行解更新不可行解档案,引导其逐渐向可行域移动,不可行解中的有用信息因此得以利用,提高了算法的求解效率。DTAMOFWA对不可行解档案进行可行性搜索的策略,消除或降低了个体对模糊时间窗约束的违反程度,有利于加速生成质量更高的可行解。

Table 2 Comparison results of verifying the effectiveness of three improved strategies on IGD and HV
4.3 所提算法的性能验证
本节实验使用的对比算法包括3种文献中已有的求解带时间窗约束车辆路径问题的算法HMOEA(Hybrid Multi-Objective Evolutionary Algorithm)[20]、hybrid DE algorithm(hybrid Differential Evolution algorithm)[21]和MOEA-FCS(Multi-Objective Evolutionary Algorithm with Fast Convergence Strategy)[22]。此外,将DTAMOFWA的多目标处理框架改为与已有多目标烟花算法S-MOFWA[23]相同的框架,编码方式、个体生成方式及约束处理方法保留不变,由此得到第4种对比算法,记为S-DMOFWA。由于对比算法对可用车辆数没有限制,因此统一在对比算法中使用本文所提消除车辆约束的解码方式。实验中DTAMOFWA和S-DMOFWA的种群规模设置为10,其余算法的种群规模为100。实验结果如表3所示。
由表3可知,针对不同规模的仿真实例,DTAMOFWA在IGD和HV上均获得了最佳平均值和标准差。根据Wilcoxon秩和检验结果可知,DTAMOFWA在所有仿真实例上的IGD和HV的平均值和标准差均显著优于4种对比算法的。可见,DTAMOFWA能够搜索到收敛精度更高、分布更加宽广、支配的目标空间体积更大的Pareto最优前沿,且算法的求解稳定性更佳。这是因为:(1)DTAMOFWA通过消除车辆约束的解码方式,将问题转化为仅带有模糊时间窗约束的问题,降低了其求解难度;(2)部分映射爆炸算子生成分布较为均匀的爆炸火花,实现了对烟花周围局部区域的精细搜索,提高了算法的收敛性;(3)利用可行性搜索产生的不可行解更新不可行解档案,保留约束违反程度较小的个体,提高了不可行解转化为可行解的概率;(4)对不可行解档案进行可行性搜索后,使产生的可行解参与可行解档案中目标驱动的启发式扩展搜索,既能增加解的多样性,又能强化算法对于当前Pareto前沿附近区域的局部搜索,使得算法的求解精度得到提高。因此,本文所提算法在每次求解过程中都能对整个可行域进行充分的探索和利用,同时挖掘不可行解的有用信息,使算法尽可能找到更多的可行非支配解。

Table 3 Comparison results of DTAMOFWA and other algorithms on IGD and HV
为了直观地比较各算法的收敛速度及精度,以C-n20-k8为例,所有算法的IGD和HV随目标评价次数变化的收敛曲线如图5所示。在每种算法运行过程中,每500次目标评价次数对IGD和HV值进行一次采样,因此在一个收敛曲线中共有100个数据点。由图5可知,在C-n20-k8上,所提算法DTAMOFWA的IGD和HV收敛精度均高于对比算法的,收敛速度也较快。在迭代初期,算法HMOEA的IGD和HV取值均最小,下降速度也超过了DTAMOFWA的,但不久后它的取值基本保持在一个较差水平。这是由于其种群规模大于DTAMOFWA的,初始解的多样性比较好,但经过一定的迭代次数后,种群开始陷入局部最优,导致所得Pareto前沿曲线在此之后基本不变。由图5还可观察到,HMOEA和hybrid DE algorithm的IGD值均在迭代前期出现了退化现象。原因可能是这2种算法缺乏精英保留机制,导致某些适应度较好的解被淘汰。所提算法DTAMOFWA由于采用有效的约束处理机制,充分利用可行解和不可行解中的重要进化信息,使得可行解档案和不可行解档案不断更新和进化。同时,变异算子使其具备一定的跳出局部最优的能力。因此,DTAMOFWA能够在前期和中期以较快的速度收敛到精度较高的近似Pareto最优前沿,并在后期保持稳定,具有更好的收敛性和多样性。在其它仿真实例上获取的IGD和HV收敛曲线也能得到类似的结论。
综上,本文所提算法是一种能有效处理约束的多目标元启发式算法,在不同规模的低碳疫苗冷链配送问题中均表现出了较好的收敛性和多样性,求解准确且稳定,并具有良好的可扩展性。

Figure 5 IGD and HV convergence curves of five algorithms on C-n20-k8
5 结束语
本文建立了低碳疫苗冷链配送问题的约束多目标优化模型。该模型以最小化企业运输成本和平均客户不满意度作为优化目标,同时满足可用车数量约束、车辆容量约束和模糊时间窗约束,更贴合实际应用,但同时也增加了问题求解的难度。针对该模型强约束条件多的特点,提出了一种双档案协同进化的离散多目标烟花算法。该算法设计了3种改进策略:采用消除车辆约束的解码方式,部分映射爆炸算子,以及双外部档案协同进化的机制。在规模递增的4个仿真实例中,分别验证了各改进策略的有效性,并将所提算法与4种已有算法进行对比实验。结果表明,所提算法在收敛性和多样性方面均优于对比算法,且对问题规模具有可扩展性,适用于求解低碳疫苗冷链配送问题这类约束多目标优化问题。
