基于指数平滑算法组合模型的玉米实时变量追肥研究

巩海亮，王熙

（黑龙江八一农垦大学工程学院，大庆 163319）

玉米中耕期追肥期应用变量施肥技术，能及时补充土壤中氮肥含量，提高作物生长所需营养[1-2]。随着玉米冠层NDVI（Normalized Difference Vegetation Index）传感器采集设备的迅速发展，变量施肥调控设备随之全面升级[3-4]，施肥设备应具备快速有效识别玉米缺氮状况，更加高效获取农田信息，实现智能化变量施肥决策，因此利用该技术应用在中耕追肥环节，补充玉米中期氮肥营养状况。

国内外对变量施肥已经开展了相关研究，于合龙等[5]采用智能算法拉格朗日乘子方法，研究设计神经网络的权值分配方案，进一步改进BP神经网络建立作物精准施肥模型，利用神经网络模型算法得出合理的玉米作物施肥量。黄丽萍[6]提出基于遗传神经网络算法应用电动施肥装置的PID的整定，解决控制系统数学模型非线性和时变不确定性，使变量施肥系统能够得到较为精确的调整施肥量。陈满等[7]构建了由转速和开度作为优先控制的双变量施肥模型，通过Bisquare估计法分析控制方法，从而确定分析系统最佳控制方案，建立变量施肥控制的序列检索表，试验分析施肥控制精度均达到90%以上，满足实际作业生产需求。董鑫等[8]针对现有灌溉系统无变量调整灌溉、缺乏灌溉决策指导的等情况，采用基于二次平滑预测算法的变量灌溉方法，根据变量调控理论，以设定参数实时调整平滑权重，快速调整灌溉系统行走步长与速度，研究结果表明，二次平滑预测算法处理的变量灌溉相对于传统灌溉效率及节水方面都具有提升。安晓飞等[9]以处方图作为变量施肥依据，设计了适合垄作玉米变量施肥的控制系统，电液比例控制技术分别控制排肥轴转速，综合考虑玉米生长指标、系统误差和最终产量数据，有效解决了肥料分层问题。但无论是无人机还是卫星遥感，都需要先采集数据经过处理后，才可以应用到变量控制环节；处方图使用空间插值的方式进行空间拟合，但无法保证未采样点数据精度，未采样点是影响施肥量准确性的重要因素；而且处方图建立需要专业的技术人员，由于处理周期长导致错过最佳施肥期，因此需要简化作业流程。研究NDVI数据实时采集并转化成实时施肥量将解决处理时间问题，但从采集到施肥由于采样频率高导致样本数据多，因此需要快速处理数据，同时也要保证施肥位置的准确性。如果使用人工智能方法直接处理[10-13]，虽然能够获得较高精度，但是需要大量训练样本完成学习过程，而且运算量大计算时间长，对于NDVI这类时间敏感数据难以保证变量施肥的实时性。

目前，较少涉及基于精准实时变量追氮技术，现有的NDVI变量施肥技术，直接将采集NDVI数据代入施肥模型，当拖拉机行驶速度过快驱动设备响应无法保证在采集点处施肥，导致实时变量施肥驱动设备准确信降低问题，实时性得不到保障。针对传统变量施肥实时性差，难以适应数据变化过快导致施肥位置准确性降低等情况，设计实时预测算法组合模型，综合利用不同单一预测模型，实现动态数据采集处理，以权值分配的形式得出具有各模型特点的综合预测模型，从而提高预测精度与判断预测趋势。

1 系统结构与工作原理

设计基于NDVI中耕变量施肥机械，其主要结构包括NDVI光谱传感器、拖拉机、车载终端、GNSS接收机、液压驱动装置、施肥机等几部分组成。首先通过NDVI传感器确定玉米冠层的归一化指标指数NDVI值，研究在有限时间内计算处理NDVI值，实时的采集获得的NDVI信息被输入到智能变量施肥决策系统，输出控制指令控制施肥执行机构，液压马达执行施肥任务完成施肥量的调整控制。整体结构如图1所示。

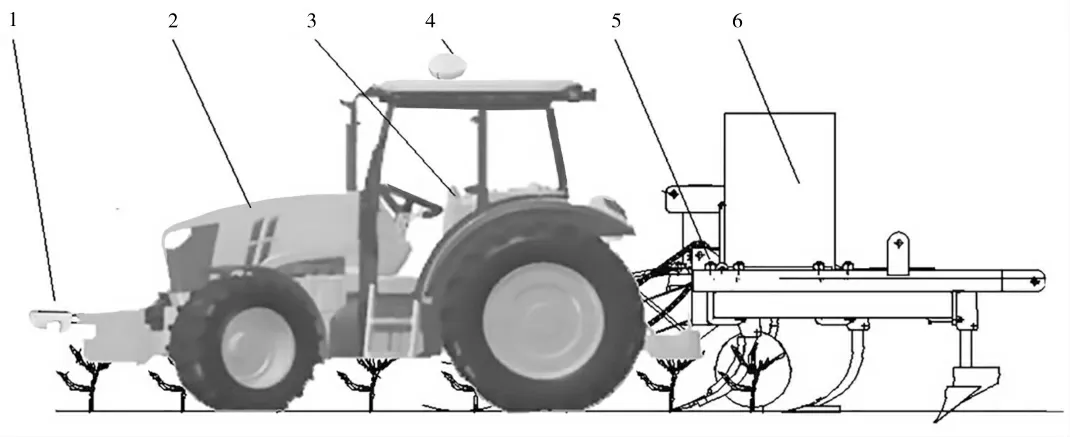
图1 采集装置主要组成设备Fig.1 Main equipment of the collection device

在中耕变量施肥进程中，使用近地光谱NDVI传感器采集作物长势数据，通过上位机施肥模型计算出对应施肥量，将处理后生成的施肥量信号发送到液压驱动装置从而进行变量施肥控制。由于整个过程是实时采集处理，拖拉机处于行进过程，并且液压驱动装置也需要一定的缓冲时间进行变控制，因此为了保证施肥准确性，需要快速预测算法对数据整理，采用一种能够适用于整个采样区间范围内的处理方法。利用已采集的历史数据对未来进行预测，采用三种指数平滑算法进行算法组合从而对数值预测，在预测值变化过程具有一定规律性，预测算法计算的数值具有准确性与实时性。

2 多模型组合实时预测算法

2.1 算法模型基本思路

光谱传感器采集系统主要功能负责采集作物长势数据，实时发送到车载计算机终端，由数据终端算法运行处理，其算法模型基本思路首先使用不同分模型，各部分模型根据历史数据为权值分配依据，同时随着数据不断变化，对各自平滑系数进行更新，在此基础上对处理后的数据进行融合，从而得到数据序列的变化趋势以及趋势发展的预测数据，其模型建立的关键因素在确定分配调整的权值和各不同模型平滑系数的更新，算法具体思路如图2所示。

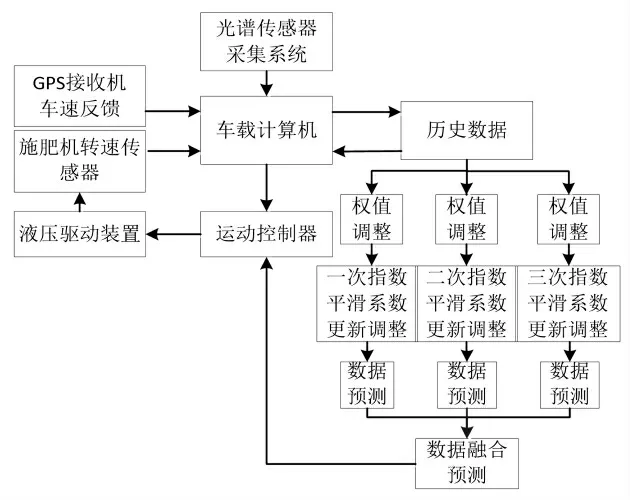
图2 算法流程Fig.2 Algorithm flowchart

2.2 多模型组合实时预测算法

指数平滑法作为一种平滑预测算法[14]，其思路主要将历史数据近期与往期分别给予不同的权重，按指数递减的规律，远离当前的数据称为远期数据，其权重越小；越接近当前的数据称为近期数据，权重越大。各平滑方法之间存在不同应用范围，对于广泛使用的一次指数平滑法，其特点普遍应用于时间序列的平滑处理，以及对无趋势数据的分析研究，对水平型历史数据的预测应用较为普遍；二次指数平滑法的应用于时间序列预测，并且多集中在线性变化研究；三次指数平滑法适合用来对数据趋势发展预测，尤其对于季节性数据分析尤为显著[15]，二次和三次指数增加均是在一次的基础上改进。为区分不同阶段采样点，将不同采样时间阶段数据将其依照时间序列分段。

（1）一次指数平滑法

平滑公式：

（2）二次指数平滑法平滑公式：

平滑预测模型：

（3）三次指数平滑法

平滑公式：

平滑预测模型：

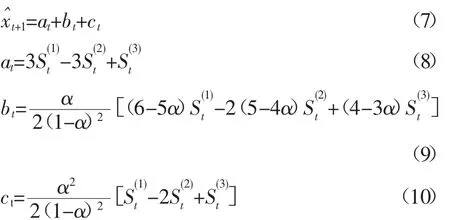
2.3 平滑系数动态调整方法

随着数据更新，以历史数据作为参考依据动态调整平滑系数a，选择计算误差最小的平滑系数作为最优平滑系数[16-18]，在接下来的数据处理过程中不断更新计算调整平滑系数。平滑系数动态调整的目的是为保证处理速度的实时性和对数据未来趋势发展的准确性，因此为了实现算法平滑系数实时动态变化的调整，在采集数据阶段实现选取最优平滑系数，采用区间遍历求解方法求解，即改进遍历求解方法在区间范围内选取，在有限区间范围的数量的平滑系数中挑选误差最小的平滑系数，下次计算平滑系数将得到更加准确数据趋势预测，这种区间遍历方法具有穷举的数据量少、运算速度快等优点。

平滑系数的初始值选取对整体数据趋势判断影响较大，因此设定参数ε，研究将ε作为平滑系数的精度求取范围，在t次采样周期时计算的平滑系数αt，在αt邻域［αt-ε，αt+ε］范围内寻找单次最优平滑系数，研究表明全局最优平滑系数在有限次迭代便可求出，其最大迭代次数为（1-ε）/ε。在数据平滑处理开始前，平滑系数α0的初始值以及权值系数被设定，用指数平滑经验方法设置平滑系数的初始值，根据预测时的历史数据，分别计算平滑系数α为αt-ε、αt、αt+ε时的数据趋势预测值，从预测误差中比较选择，误差最小的α作为下一次实际预测时的平滑系数。方法每次选择优化参数只需计算三个平滑系数，有效减少了计算频率，提高了运算效率。在没有先验知识条件下，如果α=0.05，平滑系数最多在（1-4ε）/2ε达到最优。因为参数的变化是稳定的，在参数第一次达到最优值后，之后的参数都是最优的。

2.4 动态权值组合调整方法

在使用三种指数平滑方法来平滑待处理的测量值之后，对三种方法进行加权和求和以融合数据。研究发现，初始权重只对第一次融合得到的数据有影响，对后续的趋势预测和评估没有影响。根据每个模型的前N个周期的平均误差来确定权重。具体过程如图3所示。

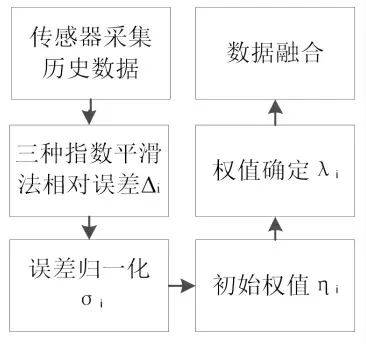
图3 权值确定流程图Fig.3 Weight determination flowchart

权值的确定首先要用到一次、二次和三次指数平滑法，分别计算采集的数据前N期平均相对误差，为其命名标记为Δ1，Δ2，Δ3，采用下列公式归一化处理平均相对误σi=Δi/∑Δj，权值分配基本思路按照小权值大误差、大权值小误差的原则。在权值分配的确定过程中，当两种模型比较时的误差均值状况过小或者过大，且二者之间误差接近时，这两种模型将会具有相同的特征，具体特征为保持同等重要或者同为无效状态，因此最终结果应保证权值基本相似。为解决非线性计算误差采用Sigmoid曲线处理，能有效避免归一化误差两极分化的问题，出现过大或者过小等情况使权重差异不显著；当两模型归一化误差趋于中间位置，误差的差异化会对导致权重产生更大的影响，设定为σ1、σ2和σ3为三种指数平滑模型归一化的平均相对误差，各部分权值的计算方法如下，按照如下公式进行加权，确定一步权值：

权值更新：

设置设定评价函数：

由于0＜Δσ，lσ＜1，因此评价函数中参数Δσ为递增函数，相反对于参数lσ是趋向于递减函数；当评价函数f（b）取最小值时，b值即为上述原则的最优值，截尾误差Δσ和线性度lσ指标被计算得出；由于b=1和b=2时sigmoid的函数均处在线性区域，与选取sigmoid曲线目要求的不符，所以b=1和b=2时，不满足要求，随b值的增加，评价函数f（b）的变化趋势如图4所示，当b=5时满足最优条件，评价函数f（b）取得最小值。

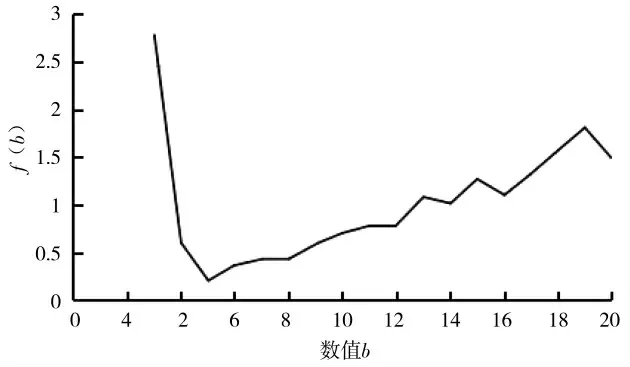
图4 函数变化趋势图Fig.4 Function change trend chart

3 试验与分析

2019年6月15日黑龙江省黑河市赵光农垦第四管理区十七作业站第10号地块，田间试验为中耕追肥阶段，坐标位置为（东经126°63′，北纬48°04′）区域，作业地块如图5所示，赵光农场地区于中高纬度地带，气温气候年平均一般0.5℃左右，海拔在240~330 m之间，选取地号四周空旷无树木遮挡问题，能有效保证GNSS定位准确，保证采集点数据位置准确性[19]。

图5 田间作业地块Fig.5 Field trial plot

研究对象是传感器测量数据的实时处理分析，在采集作业过程中设备工况良好，采样数据无异常变化，由于平滑系数的选取导致的趋势预测误差对整体影响较小[20-22]。为保证试验数据充足以及准确性，NDVI光谱传感器频率每秒采集一次，截取1 000 s区间作为仿真数据如图6所示，分析采集数据情况，由于氮肥底肥施用量不均或不足，难以支撑玉米作物后期养分需求，因此存在区域范围内作物长势不均问题。

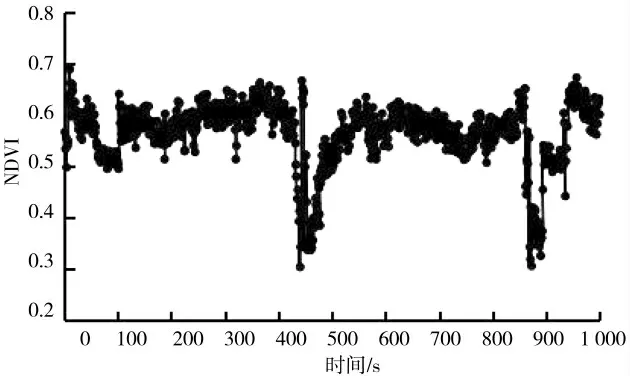
图6 部分采集数据Fig.6 Part of the collected data

以评价玉米氮素水平的NDVI数值进行实时处理，并对其趋势预测，设三种基础的指数平滑法平滑系数均为α=0.3，三种模型的权重分别为动态权值调整和动态系数调整；分析采样数据空间相关性，因此采用历史数据长度为N＝10作为数据区间范围，对4种不同算法针的预测误差如图7~图12所示。

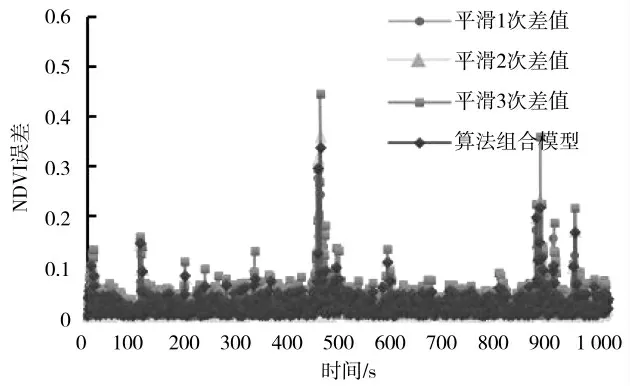
图7 一步预测误差图Fig.7 One-step prediction error

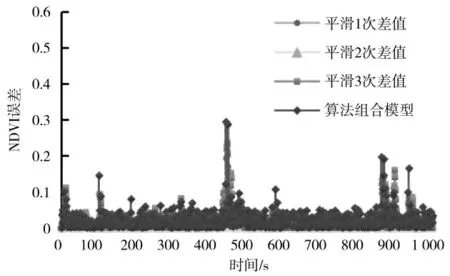
图8 两步预测误差图Fig.8 Two-step prediction error

四种数据处理方法相同采集数据的预测综合误差比较，分析表示综合预测均优于单一的指数平滑法，相比于一步平滑预测，对数据平滑效果更具有优势，其他算法对数据的追踪性更加显著，虽然存在区间范围波动，但即使在五步预测算法，其综合平均误差仅为0.154满足实际生产要求。对于田间多种复杂作业情况均能有效适应，不需要对模型算法进行训练，由于作物之间为区域相关性，研究区域范围内长势变化即可满足实际田间生产作业需求，因此数据处理过程对只需近期历史数据，有效减少对数据依赖程度提高运算速度，能够很好地在接下NDVI值对进行作物长势趋势预测，即使由于环境改变导致数值变化范围较大，基于动态调整的多模型融合算法都能够较好地数据预测。

图9 三步预测误差图Fig.9 Three-step prediction error

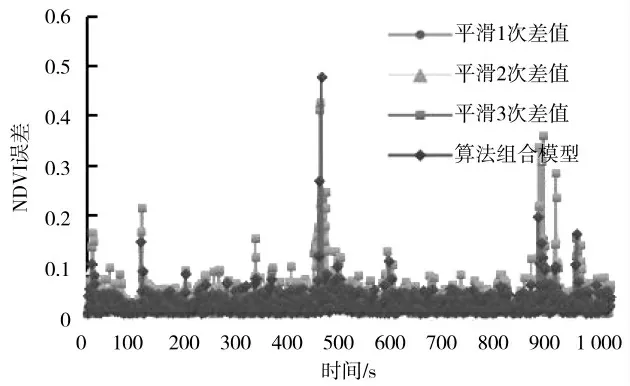
图10 四步预测误差图Fig.10 Four-step prediction error

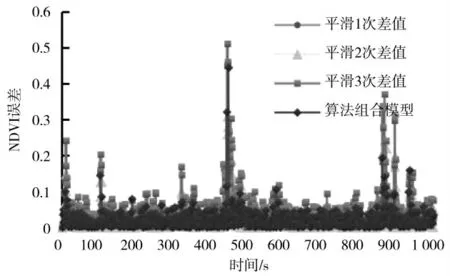
图11 五步预测误差图Fig.11 Five-step prediction error

表1 平均预测误差Table 1 Average forecast error

4 结论

在传统的指数平滑法基础上，利用各模型算法的优势进行组合，提出了一种动态多模型指数组合算法，通过对传感器采集数据进行实时处理，解决变量施肥实时处理速度与预测趋势精度问题，并且对模型算法存在的难点及问题进行分析。

（1）为解决最优平滑系数问题，使数据预测趋势精度提高，研究建立实时动态调整指数平滑法最优参数的方法，破除了在融合计算上只基于当前周期参数计算权值的局限性，以区间范围作为权值依据，更加科学合理分配各部分模型的权值，综合各平滑法的特点，将有利于评估分析最优趋势预测的变化情况。

（2）动态多模型指数组合算法与其他三种指数平滑法相比，能够更好地调整参数适应实时变化的数据处理。该算法优势为无需模型构建，算法数据分析只需权值分配合理即可满足数据趋势变化预测，处理能力强可靠性高，因此能够保证采样间隔时间满足运算分析处理时间要求，并且能够更加准确地对采集数据处理，为变量施肥技术提供可靠的数据支持。