FeSin(n=1-8)团簇结构、稳定性和红外光谱特性研究

黄 意,张 颂

(凯里学院，贵州 凯里 556001)

1 引言

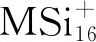
铁作为自然界中分布较广，在地壳含量仅次于铝的第一过渡金属，应用及其广泛，目前关于铁团簇的理论研究及实验研究也有，廖文裕等研究了基态及第一激发态的铁团簇Fe4与NO的反应机理[14]；周步康等通过实验研究Fe掺杂对不同导电类型Si材料电阻率的影响，得出Fe掺杂p型Si材料的电阻率远大于Fe掺杂n型Si材料的电阻率[15]。Liu Y等用Gaussion03软件包计算得出FeSin(n=1-8)团簇中FeSi5及FeSi8能隙值最大，结构最稳定[16]。相对铝-硅团簇及其他过渡金属掺杂硅团簇而言,铁掺杂硅团簇的研究还不够丰富，为丰富过渡金属掺杂硅团簇的性质研究，及对比与前人不同的方法研究铁硅团簇，本文采用DFT/B3LYP理论结合def2-svp 赝势方法研究了FeSin(n=1-8)小尺寸团簇的结构、稳定性和红外光谱特性，为铁掺杂硅团簇的的进一步研究提供理论参考。

2 计算方法

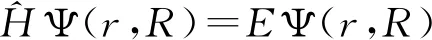
首先由DFT/B3LYP理论结合def2-svp 赝势对FeSin(n=1-8)团簇的结构进行初步优化，之后选择能量较低的几个结构再利用def2-tzvp 赝势FeSin(n=1-8)团簇进行几何结构优化和电子结构计算，所有的计算都利用弥散函数(empiricaldispersion=gd3bj)，而且，没有限制结构对称性，经计算、统计，得到了基态结构的平均结合能、能隙、极化率及电偶极矩，并将其呈现于表1中。同时，对FeSin(n=1-8)团簇基态结构进行了红外光谱模拟，研究了红外光谱的特性。

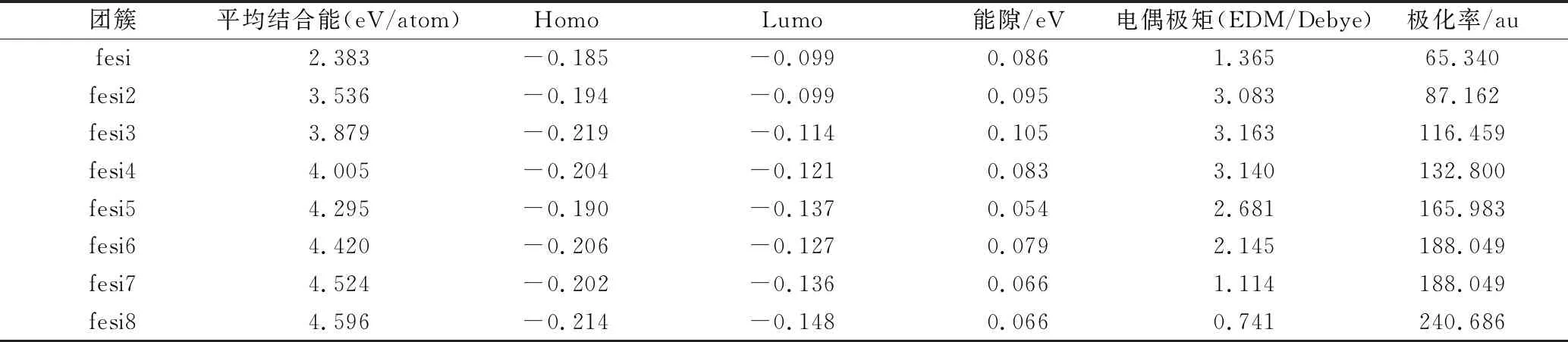
表1 FeSin(n=1-8)团簇基态结构的平均结合能、能隙、极化率及电偶极矩

3 结果与讨论

3.1 FeSin(n=1-8)团簇的结构和稳定性

3.1.1 FeSin(n=1-8)的结构

图1展现了优化的FeSin(n=1-8)团簇稳定的几何结构中的基态结构。FeSi为一维线型团簇结构，Fe原子位于团簇的一端；FeSi2为等腰三角形团簇结构，对称性为C2V，Fe原子位于三角形的顶点处，与之前研究的MSi3(M=La,Sc)基态结构一致[17]；FeSi3为平面四边形结构，对称性为C2V，Fe原子位于平面四边形的长对角的一端，这与之前研究的ZnSi3基态结构一致[18]；FeSi4为四棱锥结构，Fe原子位于四棱锥的顶部；FeSi5为四棱双锥结构，Fe原子位于四棱双锥的一端顶部 ；FeSi6是四棱双锥骨架上吸附一个Si原子的结构，Fe原子位于四棱双锥的一端顶点处； FeSi7是正方体结构，Fe原子位于正方体的一个顶点上；FeSi8为Fe原子内嵌的开放小型笼形结构。FeSin(n=1-8)团簇基态结构的生长模式大致是从一维、二维吸附结构向三维内嵌笼型结构过渡，跟过渡金属钒掺杂硅团簇VSin的结构演化规律类似[19]。

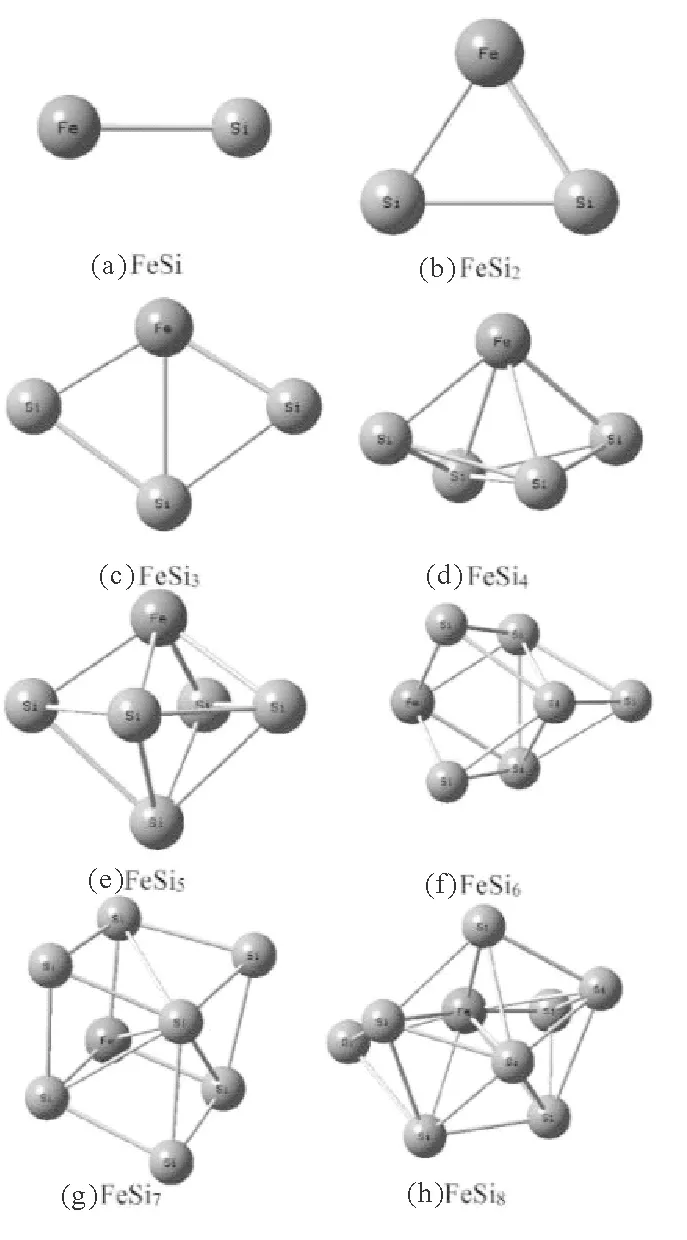
图1 FeSin(n=1-8)的基态结构

3.1.2 FeSin(n=1-8)HUMO-LUMO能隙

为了进一步研究FeSin(n=1-8)团簇的电子特性，对团簇基态结构的能隙随总原子数的演化规律进行了研究。最高占据分子轨道及最低未占据分子轨道之间的能级差称为HUMO-LUMO能隙。能隙值的大小反映了电子从占据轨道向空轨道跃迁的能力，能隙是团簇典型的电子特性之一，能隙越大，电子跃迁越难，团簇分子的化学性质越稳定。如表1及图2中FeSin(n=1-8)能隙的演化规律可知，FeSi3及FeSi6的能隙都比相邻的团簇的能隙大，说明FeSi3及FeSi6的化学性质相对稳定，其中FeSi3平面四边形结构和FeSi6四棱双锥骨架上吸附一个Si原子的结构是最稳定的基态团簇。FeSi3及FeSi6的价电子分别是16和28，前者刚好是满壳层电子数8的整数倍，后者是幻数结构[20]。FeSi5的能隙都比相邻的团簇的能隙小，也是所有团簇中能隙最小的，说明FeSi5四棱双锥结构是最不稳定的基态结构,这与Liu Y等用Gaussion03计算出的FeSin(n=1-8)团簇中 FeSi5及FeSi8能隙值最大的能隙演化规律差别很大[17]。

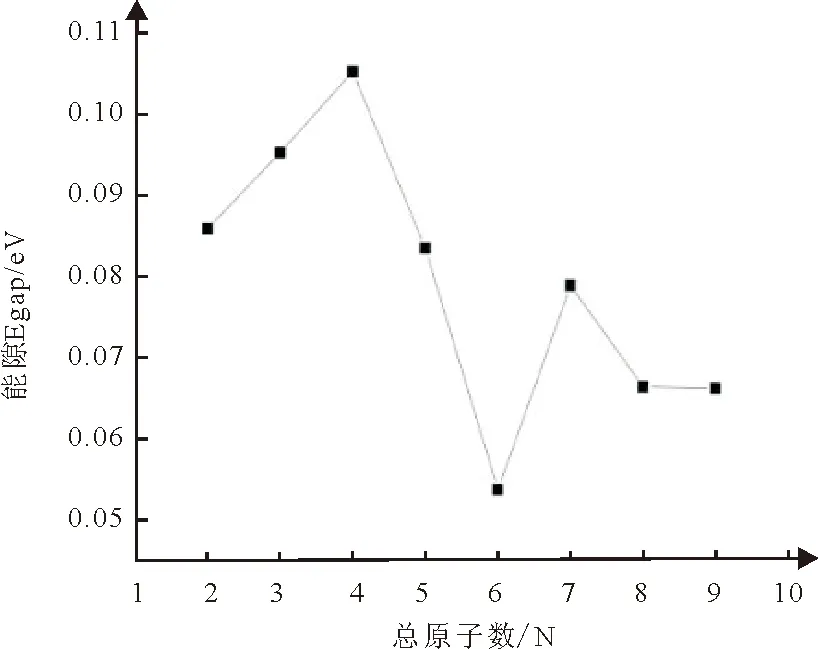
图2 FeSin(n=1-8)团簇能隙的演化规律

3.1.3 FeSin(n=1-8)的平均结合能Ea

平均结合能通常用来表征团簇结合稳定性，平均结合能越大，团簇的结合越稳定。FeSin(n=1-8)团簇的平均结合能的计算方程式[21]：

Ea(FeSin)=[E(Fe)+nE(Si)-E(FeSin)]/(n+1)

(1)

式(1)中，Ea(FeSin)表示FeSin(n=1-8)团簇的平均结合能，E(Fe)表示铁原子的能量，E(Si)表示硅原子的能量，E(FeSin)表示FeSin团簇的总能量，n表示团簇中的硅原子数。

如图3，FeSin(n=1-8)的平均结合能演化规律，FeSin(n=1-8)团簇的平均结合能Ea随总原子数的增大逐渐呈现波动式递增，FeSi团簇与FeSi2团簇之间的平均结合能增幅最大，其余相邻团簇之间的平均结合能增幅总体微小波动式递减，团簇的原子数越多，尺寸越大，平均结合能也越大,结合越稳定。

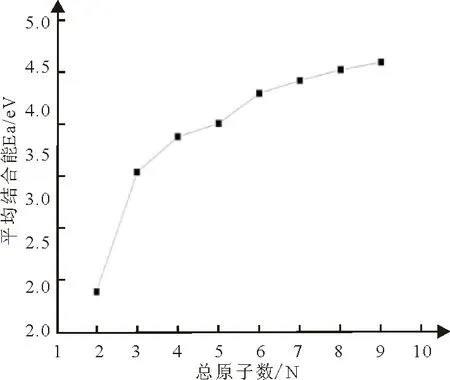
图3 FeSin(n=1-8)团簇平均结合能的演化规律

3.2 FeSin(n=1-8)团簇的电学性质

3.2.1 FeSin(n=1-8)团簇的极化率

极化率是用来反映极化难易程度的物理量，团簇的极化率也可以反映团簇中电子在空间的分布情况及对外场作用的响应的强弱情况。如表1及图4,FeSin(n=1-8)极化率的演化规律可知，随着FeSin(n=1-8)团簇总原子数的递增，FeSi团簇的极化率整体逐渐增大，除FeSi7相对FeSi6几乎没变。

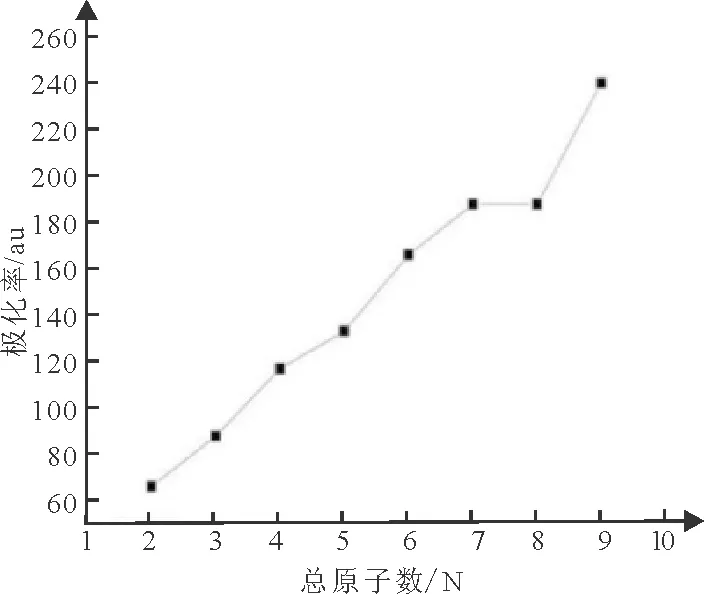
图4 FeSin(n=1-8)团簇极化率的演化规律

3.2.2 FeSin(n=1-8)的电偶极矩

团簇的电偶极矩主要描述团簇结构的极性，团簇的电偶极矩越小，其正、负电荷中心的距离越小，表明团簇具有越高的结构对称性。如表1及图5,FeSin(n=1-8)偶极矩的演化规律，除FeSi外，FeSi2、FeSi3及FeSi4团簇的电偶极矩较大，其余团簇的电偶极矩都渐渐变小，最小的是FeSi8。

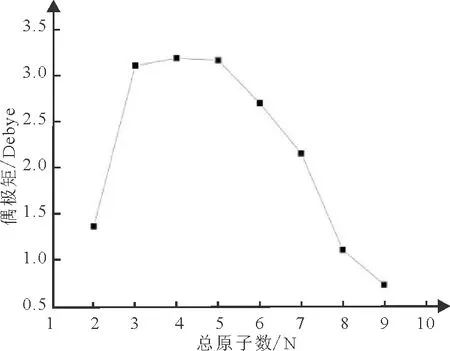
图5 FeSin(n=1-8)团簇电偶极矩的演化规律

3.3 FeSin(n=1-8)团簇的红外光谱

对FeSin(n=1-8)团簇基态结构进行了红外光谱模拟，如图6,FeSin(n=1-8)团簇的红外光谱。FeSin(n=1-8)团簇中较强的红外特征振动峰位于80～550 cm-1波段，其振动频率和强度随着团簇尺寸变化，这与李小军等对过渡金属Ti掺杂硅团簇的结论相似[22]。

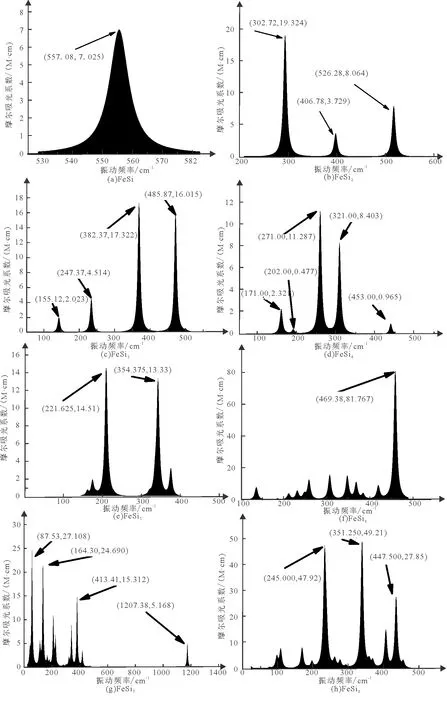
图6 FeSin(n=1-8)团簇的红外光谱

FeSi团簇频率为557 cm-1的峰值来源于Si原子和Fe原子之间的摇摆振动。FeSi2团簇频率为302 cm-1的峰值来源于2个Si原子的对称伸缩振动，频率为526 cm-1及406 cm-1的峰值来源于3个原子的对称等臂伸缩振动。FeSi3团簇频率为382 cm-1的峰值来源于2个Si原子的摇摆剪切振动，频率为485 cm-1的峰值来源于2个Si原子的对称摇摆振动以及Fe原子和其中1个Si原子的对称伸缩振动。FeSi4团簇频率为271 cm-1的峰值来源于Fe原子相对其余4个Si原子的伸缩振动，频率为321 cm-1的峰值来源于与Fe原子相连的2个Si原子之间的对称伸缩振动。FeSi5团簇频率为221 cm-1的峰值来源于与Fe原子相连的4个Si原子之间的对称伸缩振动，频率为354 cm-1的峰值来源于Fe原子以及四棱锥顶端Si原子之间的对称伸缩振动。FeSi6团簇频率为469 cm-1的峰值来源于与Fe原子相连的2个Si原子之间的对称伸缩振动以及远端Si原子的伸缩振动。FeSi7团簇频率为87 cm-1的峰值来源于Fe原子和与其相连的1个Si原子的伸缩振动和整个骨架的摇摆振动，频率为164 cm-1的峰值来源于整个骨架的摇摆振动。FeSi8团簇频率为245 cm-1及351 cm-1的峰值均来自整个结构骨架的摇摆振动，跟TiSi7团簇TiSi8团簇最强振动峰的归属一致[23]。整体来看，FeSin(n=1-8)团簇的红外光谱摩尔吸光系数随硅原子数目的增加而波动性增大，FeSi的最大摩尔吸光系数为7.025M-1cm-1，增至FeSi8的最大摩尔吸光系数49.210M-1cm-1,其中FeSin(n=2-7)团簇的最大摩尔吸光系数介于2个值之间呈波动性增大。

4 结论与展望

本次研究得到，在FeSin(n=1-8)团簇中的其掺杂 Fe原子依次吸附在团簇的棱、面及微型开放笼型结构的内部；Humo-Lumo 能级演化规律显示，FeSi3和 FeSi6团簇较相邻团簇具有较高的稳定性,与此前的研究结论 相差大，是否由于本次使用Gaussian16与此前的Gaussian03计算软件包的版本不同导致的计算结果差异，还有待增加团簇的原子数目范围，用两版本的高斯软件包做进一步计算才能确定。

通过研究FeSin(n=1-8)团簇的红外光谱主要特征峰的归属，发现稳定性较强的FeSi3团簇和 FeSi6团簇的红外光谱峰值都来源于对称伸缩振动，这表明团簇中原子之间的对称伸缩振动有易于保持团簇的结构稳定性。但是团簇原子间对称伸缩振动的机理，与其他振动形式的对比，与红外外光谱峰值的对应机制还有待进一步研究。