四轮全方位线控转向系统设计与控制方法研究

李波，白艳飞，李双双，周佳，董洪昭

（1.北京新能源汽车股份有限公司，北京 100000；2.北京工商大学 人工智能学院，北京 100048）

0 引言

现在市场上绝大多数的汽车都采用传统的前轮转向，不可否认前轮转向具有结构简单、可靠性高、占用空间小、发展成熟等优点[1]。但同时也存在低速行驶时转弯半径较大、高速行驶时转向稳定性能较差的缺点。在传统汽车的架构中，由于机械结构固定，车辆转向操作的灵活性受到很大限制，因此研究和设计一种全新的四轮全方位线控转向系统具有重大的理论意义和应用价值。

随着新能源汽车快速发展，国内外开展了高转向性能汽车技术的研究，研究人员把目光从传统的前轮转向（FWS）逐渐转移到四轮转向（4WS）和线控转向（SBW）[2]。与传统的前轮转向相比，四轮转向和线控转向可以改善汽车转向的力传递特性和角传递特性。四轮转向车辆具有四轮转角可调、四轮转矩独立可控的特点，提高了机动车辆的转向灵活性和操纵稳定性[3－4]；而线控转向使转向盘输入与汽车前轮转角之间摆脱了机械系统的限制，提升了转向特性的优化空间[5-6]。

纯电动汽车的发展使两种技术结合成为可能，以电能为动力源，通过线控技术可以实现各系统独立控制，使得四轮全方位转向的构想得以实现。李萍等[7]研究四轮转向汽车中满足阿克曼理论的转向梯形设计，提出一种基于MATLAB计算的设计观点和设计方法。夏光等[8]分析了全液压转向结构与转向偏差机理，提出一种基于转向效率的期望转向曲线及其可行域确定方法，设计了一种线控液压转向系统以实现车辆转向同步，消除转向偏差。J. W. Yong等[9]运用滑膜控制设计了一种四轮转向与直接横摆力矩集成控制算法。M. Demirci等[10]设计了一种基于拉格朗日神经网络的自适应最优控制器，用于四轮转向与直接横摆力矩的协调控制。付翔等[11]提出一种主动后轮转向和四轮转矩分配的协调控制方法，其设计的控制系统对改善四轮转向车辆高速工况下的转向灵敏度不足问题有很好的效果。

新兴的两种转向技术相较于传统的前轮转向均具有一定的优越性，但如何将两种技术的优势合理地集中到一起，成为了一个亟待解决的问题[12]。本文以设计一个全方位线控转向系统为研究目标，对一体化电动轮关键零部件即独立转向结构进行有关设计，对多模式下的上层分配策略进行相应的分析，并对下层执行电动机的控制算法进行有关仿真及实验验证，证明了设计方案的可靠性。

1 全方位线控转向系统设计

1.1 面向一体化电动轮的转向系统结构设计

线控转向系统摆脱了传统转向系统的各种限制，使转向车轮理论上可以实现360°的全方位转向[13-14]。本文所要研发的全方位线控转向系统，是以一体化电动车轮模块作为整个系统的核心，主要由独立转向机构、转向臂、轮毂电动机、主动悬架等零部件组成，具体如图1所示。

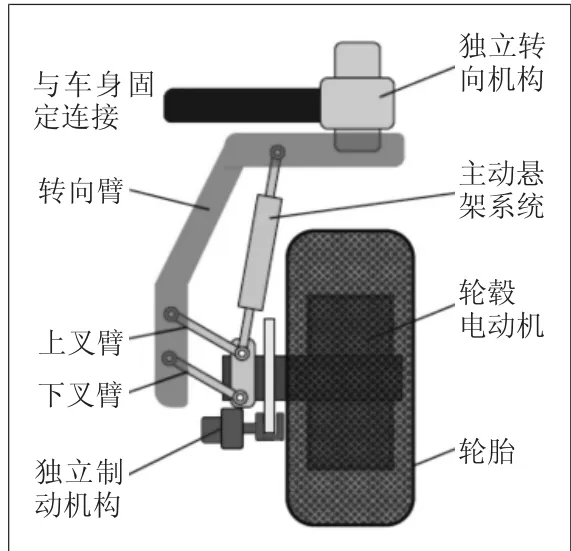
图1 一体化电动轮模块

单个车轮模块集驱动、转向、制动和主动高度调节功能于一身，高集成可拓展的模块化设计为四轮全方位线控转向电动汽车提供了一种可行的解决方案。

独立转向机构的设计是实现一体化电动车轮全方位转向的关键所在，独立转向机构采用转向电动机输出转矩经蜗轮蜗杆减速器进行减速增扭后直接带动转向臂旋转。基于此方案，一体化电动车轮可实现360°独立转向功能。图2所示为独立转向机构三维模型的结构剖面图。

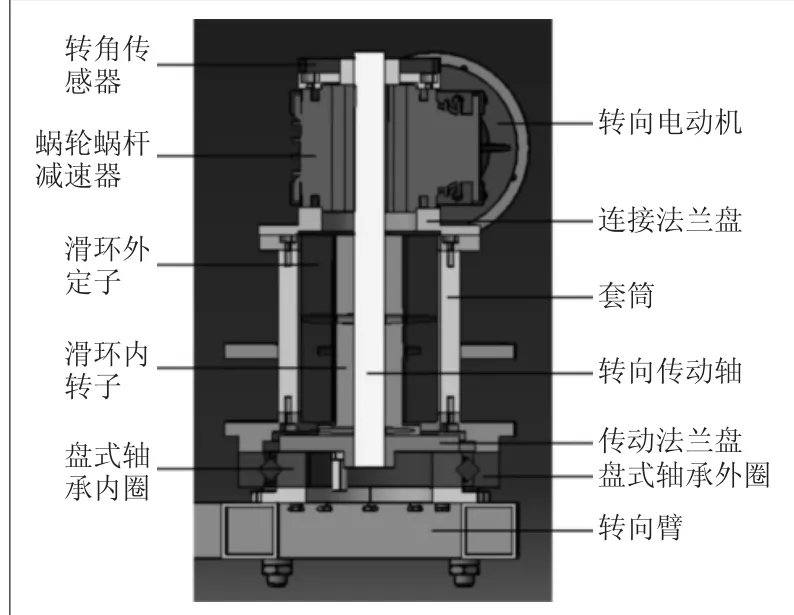
图2 独立转向机构剖面图

具体实现过程：当车轮控制器接收到方向盘转角信号后，转向电动机立刻按照设定的程序输出相应的转矩，输出转矩经蜗轮蜗杆减速器减速增扭后，由转向传动轴通过键传动带动传动法兰盘及与之固连的盘式轴承内圈，进而带动转向大臂及转向车轮旋转。其中：转角传感器可准确测量传动轴转角，即车轮转角；滑环可保证线束和管路不产生缠绕；盘式轴承可用以承受车轮模块的垂向载荷。

1.2 动力系统校核及选型

首先分别采用半经验公式、雷索夫公式、塔布莱克公式计算静态原地转向阻力矩，进行关键零部件的选型，比较计算结果，选取最大值用于校准计算[15-16]。

半经验公式：

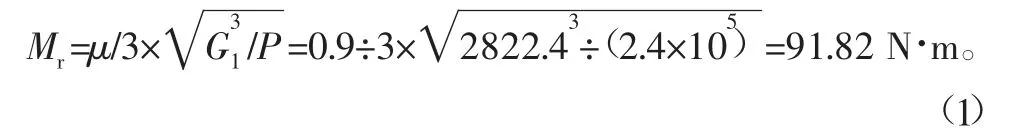
式中：μ为轮胎与地面的滑动摩擦因数（良好路面，取μ=0.9）；G1为单轴载荷（整车质量为576 kg，则单轴载荷为2822.4 N）；P为轮胎气压（GB/T 2978-2008标准规定标准型轮胎胎压为0.24～0.25 MPa，取P=0.24 MPa）。

综上计算，选取雷索夫公式计算结果用于关键零部件的选型。为保证电动机有足够大的功率克服原地转向阻力矩，以雷索夫公式的计算结果为参考值进行考虑。在此基础上还要考虑滑环外定子与内转子之间需要的启动转矩，大小约为10 N·m。

综合考虑，选择型号为FM04C的转向电动机，功率为350 W，峰值转矩为3.2 N·m。这样减速器传动比的大小就可以确定，i =Mr/Tm=188.58÷3.2=58.9，因此选择减速比大小为60：1 的 蜗 轮 蜗杆减速器。

图3 零部件实物图

通过有限元分析软件ANSYS对设计的有关零部件进行了静力分析，通过合理地划分网格、施加力和约束，分析结果如图4所示。结果满足使用要求。

图4 零部件静力分析

2 四轮转向控制算法研究

道路环境复杂多变，这就要求传统车辆驾驶员不仅要具有高超的技术及丰富的经验，还要在驾驶车辆过程中保持注意力高度集中。而车辆四轮全方位线控转向系统则可以通过4个车轮转角的合理分配，对不同环境采用不同的驾驶模式，降低驾驶员的负担，减少意外事故发生的可能性。

通过对4个车轮转角进行特定的组合，整车可实现前轮阿克曼转向、四轮阿克曼转向、楔形行驶、原地转向等驾驶模式，具备极高的机动灵活性[17]。整车转向模式示意图如图5所示。

图5 转向模式

2.1 前轮转向

传统前轮转向汽车多采用阿卡曼转向原理，如图5（a）所示，汽车转向行驶时，所有车轮绕一个瞬时中心点做圆周运动[18]。左前轮转角与右前轮转角并不相等且满足如下关系式：

式中：δfl为左前轮转角；δfr为右前轮转角；K为主销中心距；L为车轮轮距。

2.2 阿克曼四轮转向

当4个车轮同时参与转向时，也可采用阿克曼转向原理。为提高车辆在低速时的可操控性和高速时的稳定性，前后车轮转向角度由车体纵向速度决定，后轮转角通过前轮转角和纵向速度构成的比例参数获得。低速工况下，前后轮转角方向相反，以减小转弯半径；中高速工况下，前后轮转角方向相同，可以减小转向时的质心侧偏角以保持车身稳定。

假设四轮转向的瞬时中心在车辆质心的水平延长线上，如图5（b）所示，则满足如下关系：

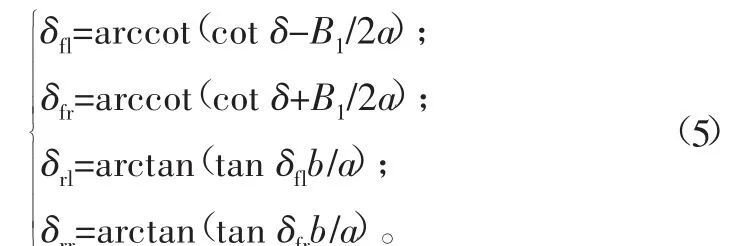
式中：δfl为左前轮转角；δfr为右前轮转角；δrl为左后轮转角；δrr为右后轮转角；δ为等效前轮转角；a、b分别为质心到前、后轴的距离；B1、B2分别为前、后轮轮距。

2.3 楔形行驶

如图5（c）所示，当前、后轮进行同相位、同角度的转向，如同时向左转动45°，即为楔形转向模式，可进行快速换道，使车辆实现“点对点”的无横摆行走，提高车辆高速行驶时的转向稳定性。对于楔形行驶模式下的方向盘转角与车轮的转角传动比，比率越低，汽车反应越灵敏；比率越高，车轮转向达到指定距离方向盘所需的旋转幅度越大。如果传动比太小，会使得楔形转向过于灵敏而导致产生不安全因素，因此楔形模式下的方向盘与车轮传动比不宜设置过小。同时考虑到楔形模式多用于变道超车或狭窄路面驾驶环境，为了避免给驾驶员带来过大的转向负担，将楔形的传动比设置为类似于传统车辆常规的传动比14:1，即驾驶员使方向盘转420°时，车轮转角为30°。并且当车轮转角超过30°时，车轮保持在最大转角不变。

2.4 原地转向

当行经狭窄巷道或乡间小路并偶遇前方来车，需有一方让行才可通过时，倒车是唯一的选择。而通过原地转向模式，则可在运动受限的狭窄空间下进行掉头转向操作，提高了车辆在狭窄空间下的机动性能。

已知实车前后轴距L为1560 mm，左右轮距B为1254 mm，则原地转向直径D=（L2+B2）1/2≈2002 mm。定义车轮转角以逆时针方向为正，则各车轮转角为：

3 永磁同步电动机控制算法研究

永磁同步电动机具有结构简单、效率高、体积小、功率因数高等特点，在工业领域得以广泛应用[19]，故转向电动机采用型号为FM04C的永磁同步电动机。为使系统便于分析，作如下几点假设：1）忽略电动机铁心的饱和；2）不计涡流和磁滞损耗；3）转子上没有阻尼绕组。建立永磁同步电动机数学模型如下。

3.1 三相静止坐标系下的数学模型

电压方程：

3.2 永磁同步电动机d-q轴数学模型

实际输入电动机电枢绕组的是三相交流电流iU、iV、iW，因此需要经过坐标变换求出id和iq。经过Clark、Park变换，完成由静止的abc坐标系到同步旋转的dq坐标系的变换（等功率变换）为:

3.3 矢量控制

矢量控制实际上是对电动机定子电流矢量相位和幅值的控制。当永磁体的励磁磁链和直、交轴电感确定后，电动机的转矩便取决于定子电流的空间矢量is，而is的大小和相位又取决于id和iq，通过控制id和iq便可以控制电动机的转矩[20]。其中，id和iq为定子电流两个互为正交的分量，分别代表了电流励磁分量和转矩分量。

为实现PMSM对目标车轮转角快速而精确的响应，采用位置速度电流三闭环控制，分别实现电动机的位置、速度和转矩控制。如图6所示，以目标转角δ与实际车轮转角δi的差值作为位置环的输入，其输出信号作为目标速度u，并与实际车轮转速ui计算偏差后，作为速度环的输入。

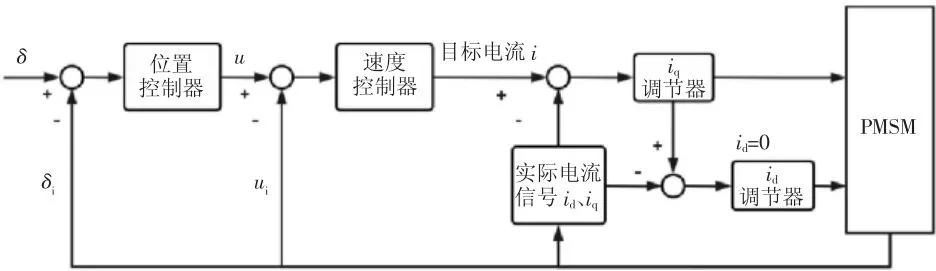
图6 位置速度电流三闭环控制结构框图

速度控制器的输出即为目标电流（转矩），由式（12）坐标变换得来的实际电流信号与目标电流的差值经电流环、反Park变换和空间矢量脉宽调制后，即可得到作用在电动机三相电压的指令值，实现电动机的控制[21-22]。

图7所示为试验平台所采用的转向控制器实物图，主要由电源芯片、MCU、电动机驱动芯片、Can芯片等组成，控制逻辑如图8所示。

图7 转向控制器

图8 转向控制器电气架构图

4 仿真与台架测试

4.1 转向模式仿真

在完成转向控制系统的理论分析和数学建模后，本文利用Carsim与Simulink对楔形行驶及原地转向两种典型的转向模式进行了联合建模仿真，研究车辆的运动情况及关键参数的变化，以获取最直观的实验数据。车辆的有关参数如表1所示。

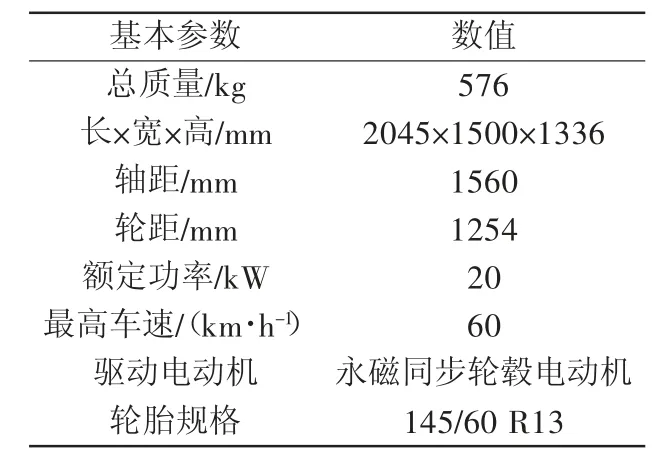
表1 整车参数表

4.1.1 楔形行驶仿真由图9可以看出，当车辆进行45°楔形行驶时，质心运动轨迹近似是一条斜率为-1的直线，而横摆角速度在0附近进行波动，能够保证车辆行驶安全性，满足预期的设想。

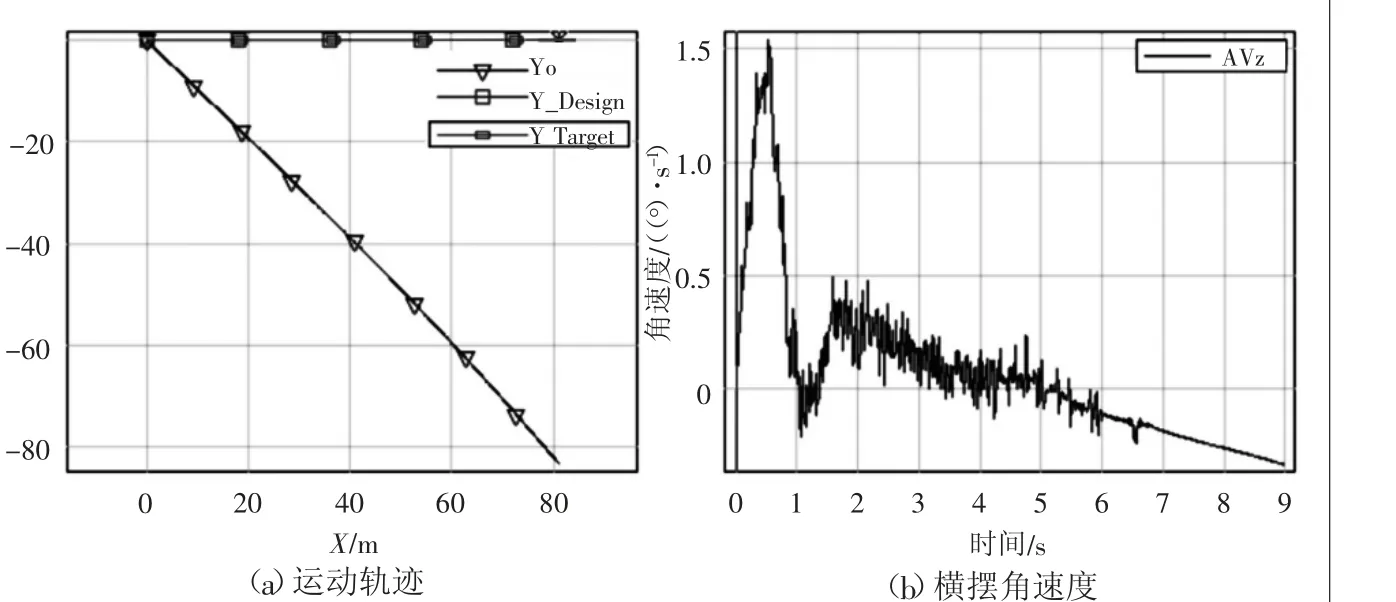
图9 45°楔形行驶

4.1.2 原地转向仿真

图10为Carsim与Simulink联合仿真的结果，通过设定4个车轮转角并给予不同的驱动力矩，仿真结果表明车辆质心的轨迹始终为一个点，即车辆绕着质心原地旋转，说明了原地转向的机动灵活性。

图10 原地转向

4.2 永磁同步电动机三闭环仿真

基于在Simulink中搭建的永磁同步电动机模型，采用位置速度电流三闭环控制策略进行定转角控制仿真，如图11所示[23-25]。通过给定一个90°的阶跃参考位置信号，从图12（a）中可以看到实际位置在极短时间内稳定地跟随上参考位置，并且没有超调量和静态误差。在此之后实际位置、电磁转矩、转速和三相电流均趋于稳定。具体结果如图12所示。

图11 PMSM三闭环仿真

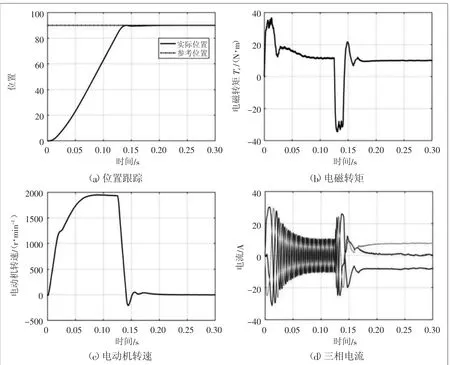
图12 仿真结果图

4.3 台架测试

基于前文设计的全方位线控转向系统，搭建的一体化电动轮实验台架如图13所示。台架主要由一体化电动轮、转向控制器、12 V蓄电池、支撑架等组成。

图13 一体化电动轮试验台架

通过可视化调试工具FreeMaster进行在线调试，借助可视化窗口可直观地观测到相应参数的变化情况，从而验证控制器烧录程序的合理性及可靠性。

从图14的实验数据中可以看出，通过给定90°的目标车轮转角，在位置速度电流三闭环控制的模式下，实际车轮转角（转速、电流）都可以在极短的时间内跟随上目标转角（转速、电流）并保持稳定，并且实际车轮转角与目标转角的偏差最终能够维持在2°以内，这与我们的程序设定是相一致的，表现出较好的跟随效果，验证了一体化电动轮结构的可靠性及控制程序的合理性。

图14 三闭环大转角跟随情况

5结语

为摆脱传统转向机构的束缚，探究新型的转向机构，实现四轮全方位线控转向的目标。本文分别从以下几个方面出发进行设计：1）首先，介绍了单个一体化电动轮的结构组成，对关键目标——独立转向机构的机械结构进行了设计，对关键零部件进行了选型计算，并对受力部件进行有限元静力分析；2）针对不同驾驶模式下四轮转角不同的情形，设定了不同的转角分配策略，通过仿真的方式分析了典型模式下关键参数的变化，表明各转向模式在不同驾驶环境的优越性；3）为实现车轮的全方位线控转向，基于永磁同步电动机工作原理设计了三闭环控制策略，并进行了相应仿真与台架实验验证。本文针对四轮全方位转向系统的设计进行了一系列的研究，证明了设计方案的可行性，为新一代汽车转向系统的设计提供了一种全新的思路。