矿车车体振幅影响因素及其影响规律研究
2022-12-21熊志远赵娜赵阳邬玉斌
熊志远, 赵娜, 赵阳, 邬玉斌
(北京市科学技术研究院 城市安全与环境科学研究所,北京 100054)
0 引言
矿车运输在国内中小型煤矿得到广泛应用,它是一种既适用平巷、又适用倾斜井巷的辅助运输方式[1-3]。实际上,矿车在轨道上行驶时,普遍存在车体振动现象,而且随着煤矿生产能力的提高,矿车运输向重载、高速方向的发展,振动程度越来越剧烈。车体的剧烈振动将增大矿车内部各零部件之间的摩擦和损伤;将增大矿车对钢轨的作用力,加剧轨道变形。车体振动不仅增加了矿车运输系统的维修成本,而且还有可能使矿车之间的连接销弹出,导致跑车[4-5]事故。
为了有效控制车体振动、保证矿车平稳运行,科研工作者进行了一些尝试性的研究探讨。文献[6]针对矿车越过钢轨接头错牙(两相邻轨道在连接处没有整齐对接而产生的台阶)时产生的振动进行了研究,结果表明,车体与车轴之间连接系统的阻尼系数越大,车体振幅越小,增加连接系统阻尼系数有利于矿车平稳运行。文献[7]针对矿车在波形钢轨上行驶时产生的振动进行了研究,结果表明,增大连接系统阻尼系数、保持车速在小于3 m/s或大于7.32 m/s的范围内行驶均能降低车体振幅。文献[8]针对矿车越过钢轨接头错牙时产生的振动进行了试验研究,探讨了错牙尺寸、车速、车体载重3参数变化对矿车振动的影响。
文献[6]研究了连接系统阻尼系数对车体振幅的影响;文献[7]研究了阻尼系数、车速对车体振幅的影响;文献[8]试验研究了钢轨错牙尺寸、车速、车体载重对车体振幅的影响。本文将基于文献[7]继续研究车体质量、连接系统刚度、钢轨波长和幅度对车体振幅的影响。本研究既为文献[8]的试验研究给予一定的理论补充,又为控制矿车车体振动提供新的理论参考依据。
1 理论模型
图1是1/4矿车在波形轨道上行驶的模型示意图。1/4车体简化为没有弹性和阻尼、质量为m的刚性质量块。车体与车轴之间的连接系统简化为没有阻尼和质量、弹性常数为k的弹簧与没有质量和弹性、阻尼系数为c的阻尼器的并联结构。同时,将车轮与钢轨视为刚性材料,钢轨按y1=asin(2πx1/l)(其中:l为波长,a为幅度)规律起伏,坐标原点及坐标系O1x1y1的位置如图1所示。
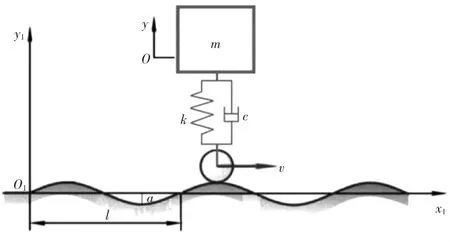
图1 1/4矿车在波形轨道上行驶的模型示意图
以车体m为研究对象,取m在水平轨道上的平衡位置为坐标原点,建立随车轮一起前进、铅垂方向的Oy轴,如图1所示。根据牛顿第二定律,列出车体运动微分方程:
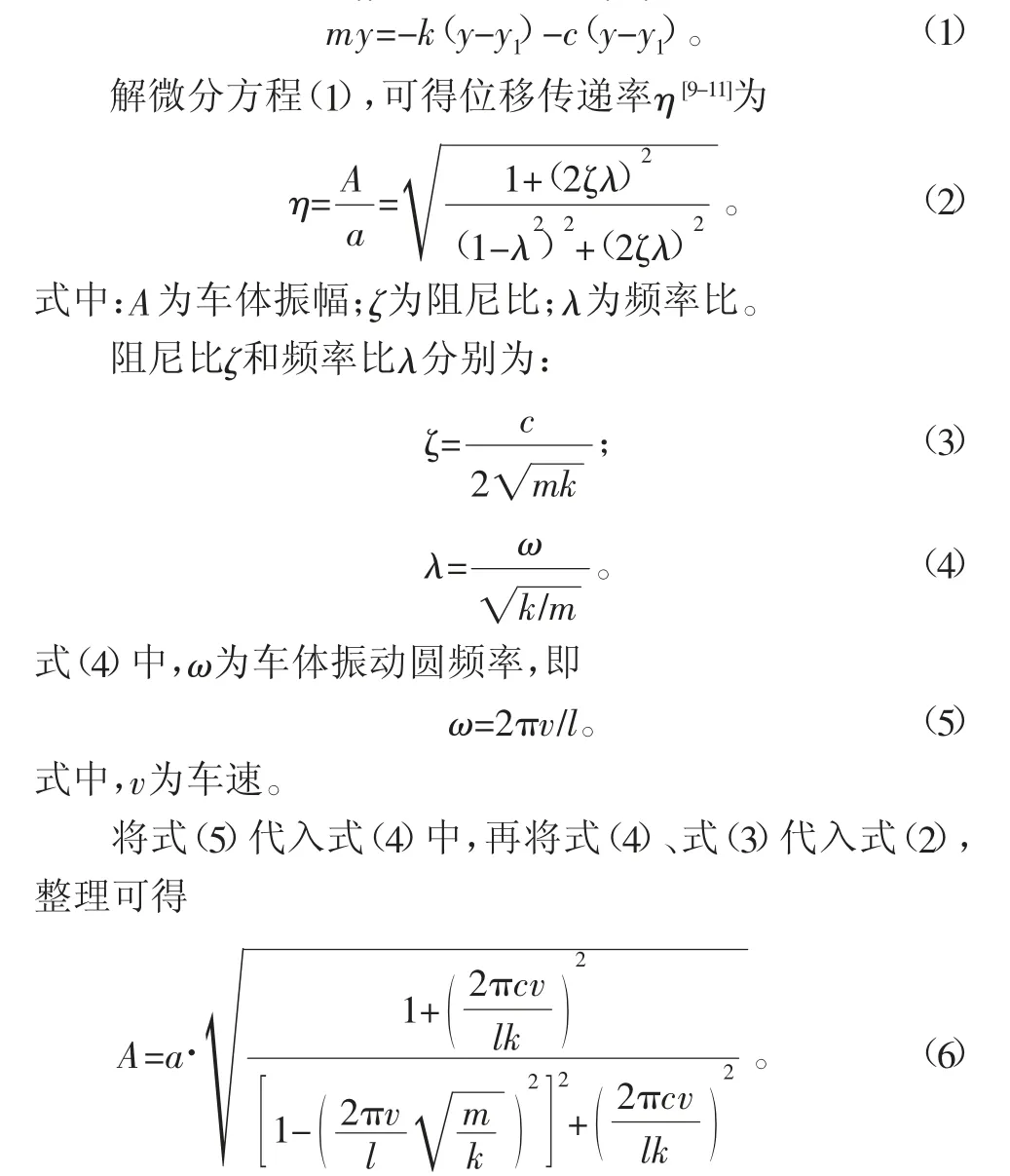
从式(6)可以看出:车体振幅A一共与6个参数相关,其中,m、v为与车体相关的参数;k、c为与连接系统相关的参数;l、a为与轨道相关的参数。但是仅从式(6)看不出各参数与车体振幅之间的变化规律。文献[7]已探讨了阻尼系数c、车速v对车体振幅的影响,下面将继续探讨车体质量、连接系统刚度、钢轨波长和幅度对车体振幅的影响规律。
2 车体振幅影响因素及其影响规律
某一大型矿车,1/4车体质量m为950 kg。车体与车轴之间连接系统的刚度系数k为85 kN/m、阻尼系数c为2800 N·s/m。矿车以3.5 m/s的速度v在波长l为4 m、幅度a为10 mm的波形钢轨上匀速行驶。将上述参数代入式(6),计算得车体振幅A为14.8 mm,相关参数统计于表1中。

表1 车体振幅及其影响参数
2.1 车体质量对车体振幅的影响
将表1中的相关参数代入式(6)中,其中只允许车体质量m发生变化,作出车体振幅A与车体质量m的变化关系曲线,如图2所示。曲线表明:随着m的增加,A显著升高,经过一个峰值后,快速下降并趋于平稳。将m=0代入式(6)得:A=a=10 mm,与图2中曲线的起点位置相符。图2中,m=950 kg时,对应A=14.8 mm,与表1中的数据相符。根据式(6),视m为变量,由分母最小、A最大可得
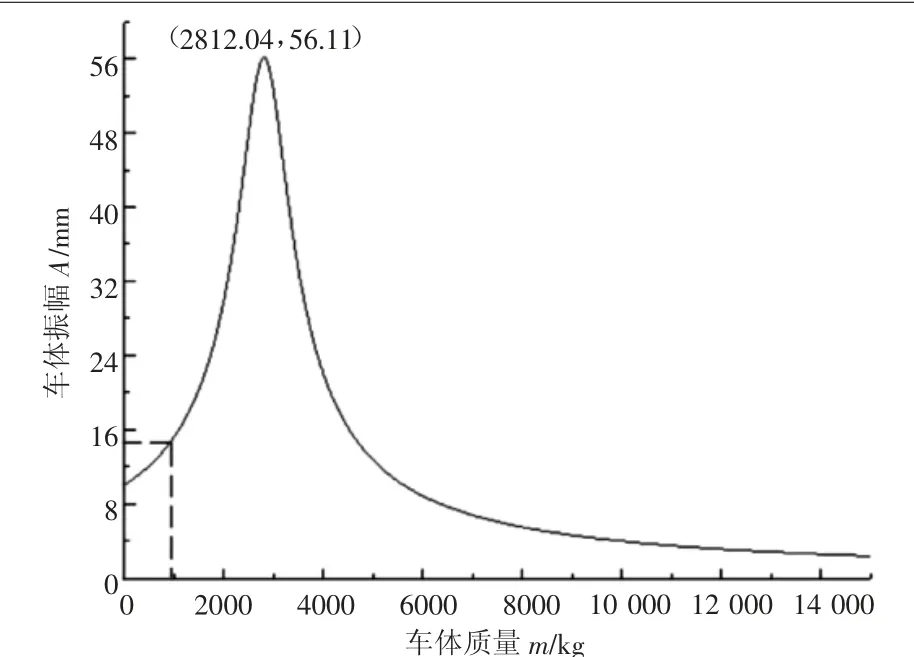
图2 车体质量与车体振幅的变化关系

2.2 刚度对车体振幅的影响
将表1中的相关参数代入式(6)中,其中只允许刚度k发生变化,绘出车体振幅A与刚度k的变化关系曲线,如图3所示。曲线表明:随着k的增加,A先急剧上升,经历一个波峰后,逐渐下降,并趋于平缓。
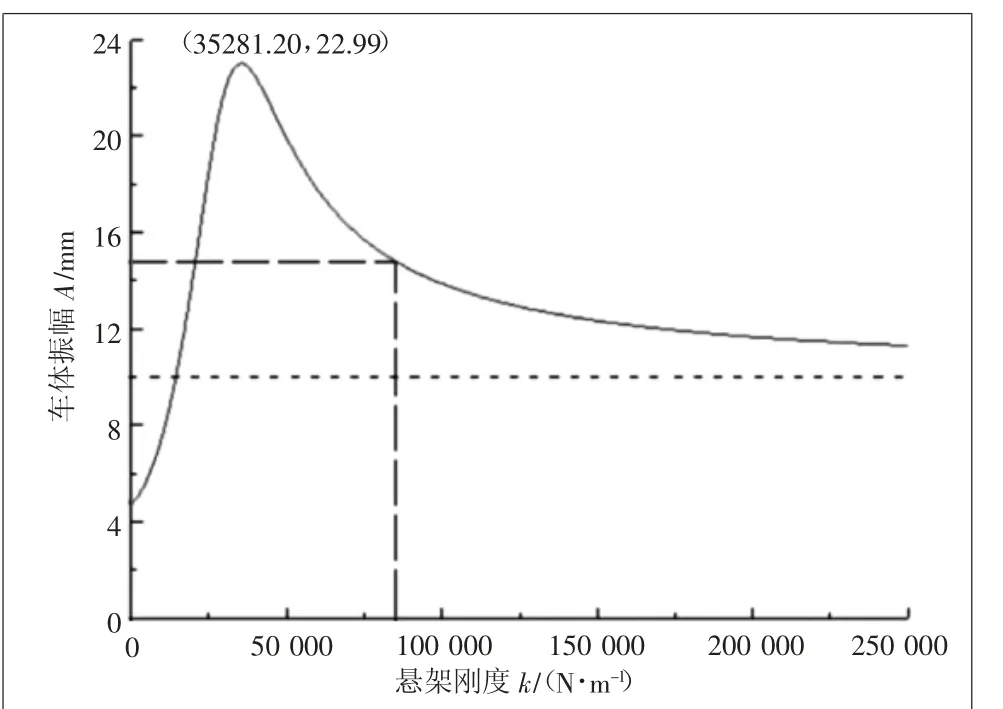
图3 车体振幅与刚度的变化关系


图4是式(11)所表示的二次抛物线在坐标系中的示意图,k2的左邻域为正值、右邻域为负值,所以k2对应A的极大值。将表1中的相关参数代入p=2πv/l,计算得p=5.50;再将p及表1中的m、c代入式(12),计算得k2=35431.06 N/m;最后,将p、k2及表1中的相关参数代入式(9),计算得A=23.00 mm。理论计算的极大值(35 431.06,23.00)与图3中的峰值(35 281.20,22.99)极为接近。图3中,当k=85000 N/m时,对应A=14.8 mm,与表1中的数据相符。
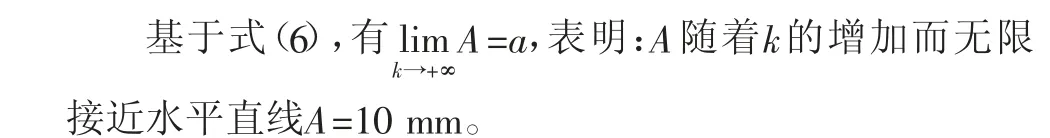
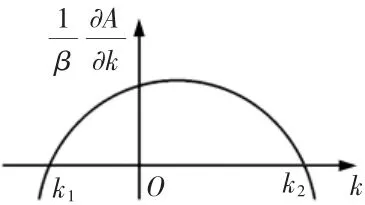
图4 二次抛物线示意图
2.3 波长对车体振幅的影响
将表1中的相关参数代入式(6)中,其中只允许波长l发生变化,绘出车体振幅A与波长l的变化关系曲线,如图5所示。曲线表明:随着l的增加,A急剧增加,经历一个波峰后,快速下降,而后趋于平缓。
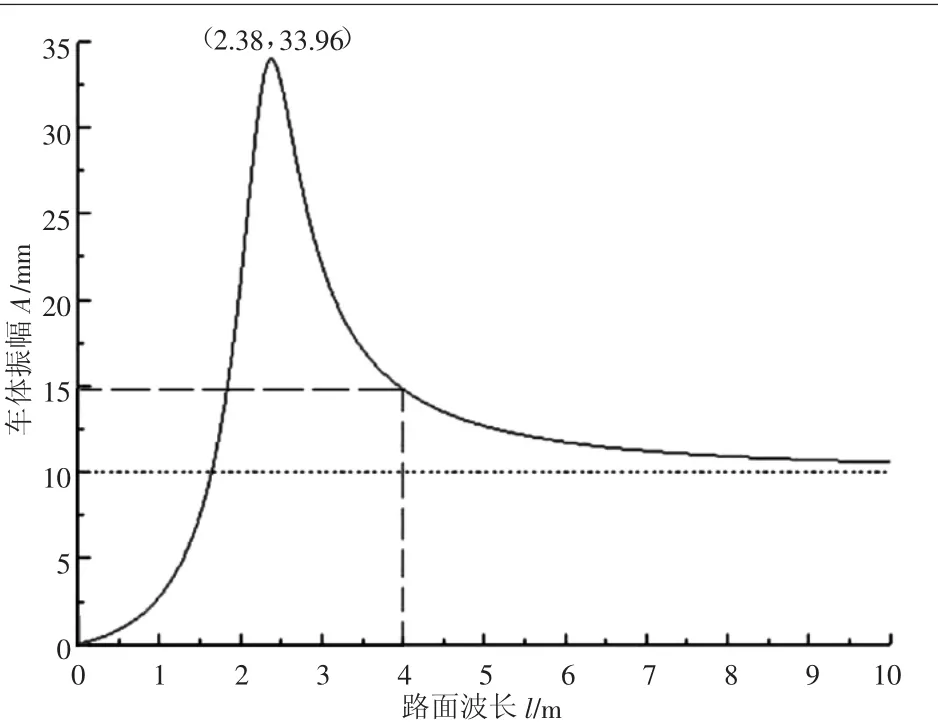
图5 车体振幅与波长的变化关系


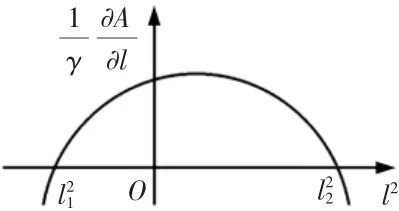
图6 二次抛物线示意图

2.4 幅度对车体振幅的影响
将表1中的相关参数代入式(6)中,其中只允许幅度a发生变化,绘出车体振幅A与幅度a的变化关系,如图7所示。由图7可知,随着a增加,A也线性增加,A与a成正比例关系。由式(6)可知,直线斜率为
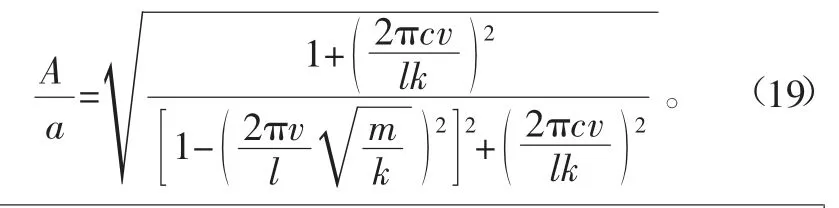
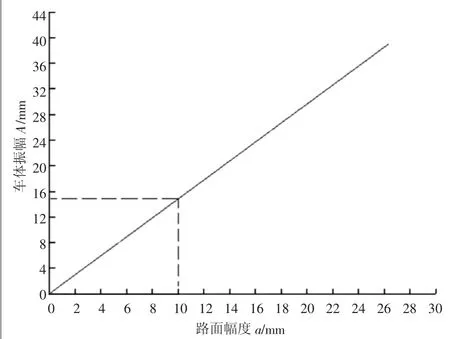
图7 车体振幅与幅度的变化关系
将表1中的相关参数代入式(19),计算得斜率A/a为1.48。另外,由式(6)可知,当幅度a=0时,车体振幅A也为0,与图7中的直线起点位置一致。图7中,a=10 mm时,对应A=14.8 mm,与表1中的数据相符。
3 结论
本文建立了煤矿矿车车体振动理论模型,分析了车体质量、连接系统刚度、钢轨波长和幅度分别对车体振幅的影响规律。得到如下结论:1)随着车体质量或连接系统刚度或钢轨波长的增加,车体振幅先是快速增加,经过一个波峰后,随即显著下降,而后趋于平缓;2)随着钢轨幅度增加,车体振幅也线性增加,它们成正比例关系。
