多重接触式静密封泄漏特性定量分析模型
2022-12-21赵飞张晓妹刘鸣王立权
赵飞,张晓妹,刘鸣,王立权
(1.首都医科大学附属北京朝阳医院 高压氧科,北京 100020;2.黑龙江省城镇住宅建筑工程有限公司,哈尔滨 150000;3.哈尔滨工程大学,哈尔滨 150001)
0 引言
接触式静密封是通过两表面的相互接触挤压实现的,宏观上看似平整的加工表面和自然表面均具有表面粗糙度,当两表面相互接触时,表面粗糙度使得实际接触面积小于名义接触面积,由于接触区域存在微小孔隙,为密封介质的泄漏提供了可能。为了以较为经济的方式获得较好的密封性能,常采用多重接触式静密封,通过在泄漏方向上布置2个或2个以上密封区域,可以显著提高整体的密封性能,因结构形式简单,密封效果好,广泛应用于海洋工程装备、石油化工装备、机械工程、建筑等领域。
近年来,国内学者提出了各种多重密封结构并开展了相关研究。韩飞[1]研究了浮顶储罐双密封结构,提出了在一二次密封空间填充密封物质的方法,抑制油气聚集,降低安全隐患;宫乙帅等[2]研究了齿轮泵的双密封结构,说明了双密封可以显著提高齿轮泵对外密封的可靠性;梁宁[3]分析了潜水潜污电动机电泵动的多重密封技术,说明了多重密封技术可以减少压力梯度、降低泄漏量;张旭东等[4]提出了一种用于铅蓄电池的双重密封结构,通过实验证实了双密封结构具有显著提高对电池内部酸液的密封性能,可有效提高电池的安全性和寿命;魏宗亮[5]提出了一种解决海底破损管道快速修复问题的水下连接器卡压式水下连接器,该装置采用双密封结构,可有效提高油气介质密封的可靠性。国内高校在接触式静密封泄漏特性定量分析方面开展了深入的理论研究工作。史建成等[6]提出了一种基于逾渗模型的接触式静密封泄漏量预测模型,分析了接触面积、表面纹理方向对泄漏特性的影响;黄晓明等[7]基于MB模型和分形多孔介质理论,研究了金属平垫片的泄漏特性;Hu等[8]将分形接触模型用于气体密封动态性能研究;Liu等[9]研究了水下连接器的密封特性,提出了流阻模型,给出了密封区域流阻、两端压力梯度和泄漏率的数学关系。
由以上分析可知,现有的研究工作对单密封的泄漏特性进行了深入研究,但对于多重接触式静密封的泄漏机理研究较少。本文提出一种多重接触式静密封理论模型,通过数值仿真分析了密封区域数量、密封区域间体积对泄漏特性的影响,为设计多重接触式静密封结构和定量分析其密封性能提供了参考。
1 理论模型
应用于不同领域、形式多样的多重接触式静密封具有相似的结构和特点,提取关键特征,可简化为一般性理论模型,包括密封腔体、腔体内壁、密封介质、密封区域、密封空间等,如图1所示。密封圈与腔体内壁相互挤压形成密封区域,由于表面粗糙度的存在,密封圈与腔体表面存在不完全接触,形成泄漏通道。两个相邻密封区域可以形成一个密封空间。密封腔体内的液体密封介质具有较高压力,在高压驱动下通过密封区域和密封空间向低压端泄漏,即密封腔体内液体密封介质在压力差作用下,以一定的流量进行泄漏。
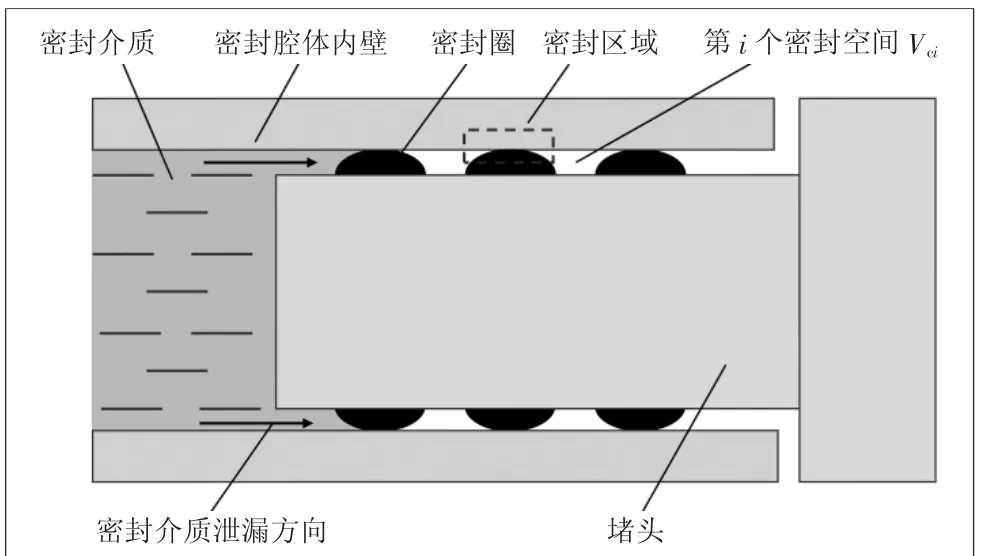
图1 多重接触式静密封的一般性结构示意图
多重接触式静密封的泄漏过程如图2所示。在泄漏过程中,靠近高压端的密封空间优先被液体充满,且液体达到一定压力后,才能继续沿相邻密封区域向下一密封空间泄漏,定义为密封区域的首次稳定泄漏状态。密封介质沿压力下降方向,经过数个密封区域和密封空间泄漏,最终向外界环境泄漏,定义为多重接触式静密封的首次稳定泄漏状态。

图2 多重接触式静密封的泄漏过程示意图
为简化问题,本文提出以下假设:1)将液体密封介质视为不可压缩流体,忽略液体压力对液体体积的影响,满足流体连续性假设,密封介质流经密封区域的泄漏率相等。2)将液体密封介质泄漏过程视为理想状态,忽略液体沿密封区域泄漏的非稳定泄漏情况,如密封空间内液体压力累积过程、密封区域两端压力差不稳定情况、液体介质未完全贯通密封区域情况等。3)忽略密封空间内气体压力对液体密封介质泄漏的影响,将其等效为外界环境。
多重接触式静密封的密封空间数量为

多重接触式静密封第i个密封空间体积为Vci,可根据体积与泄漏率关系,得到第i个密封区域空间内充满密封介质的时间,定义为第i个密封区域首次稳定泄漏时间:

密封介质流经多重接触式静密封最后一个密封区域的时间,定义为首次发生稳定泄漏的时间:

对于某些要求无泄漏的工况,如油气管道、建筑防水等,一般以最后一道密封出现泄漏为密封失效。
2 数值仿真结果与讨论
2.1 总流阻不同条件下的泄漏特性分析
考虑一系列多重接触式静密封,给定密封区域数量ns=1~8,压力梯度为1 MPa,密封区域均采用相同流阻的密封单元,任一密封区域流阻Ri为5000、10 000、15 000 MPa·s/mL。
通过式(3)计算得到多重接触式静密封的密封区域数量与总流阻关系,如图3所示。当密封区域流阻相同时,总流阻R与密封区域数量ns呈线性关系;当密封区域数量相同时,任一密封区域流阻Ri越大,总流阻越大。
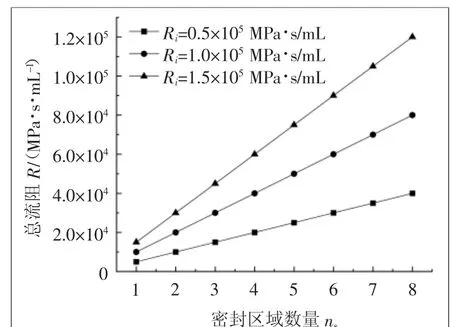
图3 密封区域数量与流阻关系
通过式(5)计算得到多重接触式静密封的密封区域数量与稳定状态下泄漏率关系,如图4所示。密封区域流阻相同时,随密封区域数量ns增加,稳定状态下泄漏率QL显著降低,呈现非线性关系;当密封区域数量相同时,任一密封区域流阻Ri越大,泄漏率QL越小。

图4 密封区域数量与泄漏率关系
给定任意密封空间体积为Vci=10.0 mL(10.0×10-6m3),分析不同密封区域流阻Ri对密封区域数量ns与首次稳定泄漏时间关系的影响。
由式(6)计算得到密封区域数量与第i个密封区域首次稳定泄漏时间ti的关系,如图5所示。对于单密封结构(ns=1),忽略密封区域的不稳定泄漏时间,认为密封介质稳定泄漏时间为0。对于双密封结构(ns=2),当其唯一一个密封空间被密封介质充满时,认为其处于稳定泄漏状态,以此类推,对于ns重密封结构,第i个密封空间充满液体的时间ti,随密封区域序号i增加而线性增大。由式(6)可知,密封区域数量ns不同的多重接触式静密封,第i个(i≤ns,ns>1)密封区域首次稳定泄漏时间ti相同,其与已发生稳定泄漏的密封区域情况相关,与密封区域总数ns无关,出现图5所示的数值曲线重合情况。

图5 密封区域数量对第i个密封区域首次稳定泄漏时间的影响
由 式(7)可得,密封区域流阻对首次发生稳定泄漏时间的影响,如图6所示。随密封区域数量ns增加,首次稳定泄漏时间T 非线性增大;当密封区域数量ns相同时,密封区域流阻Ri越大,首次稳定泄漏时间T越大。这是由于流阻降低了泄漏率,液体密封介质需要更长时间才能充满密封空间。
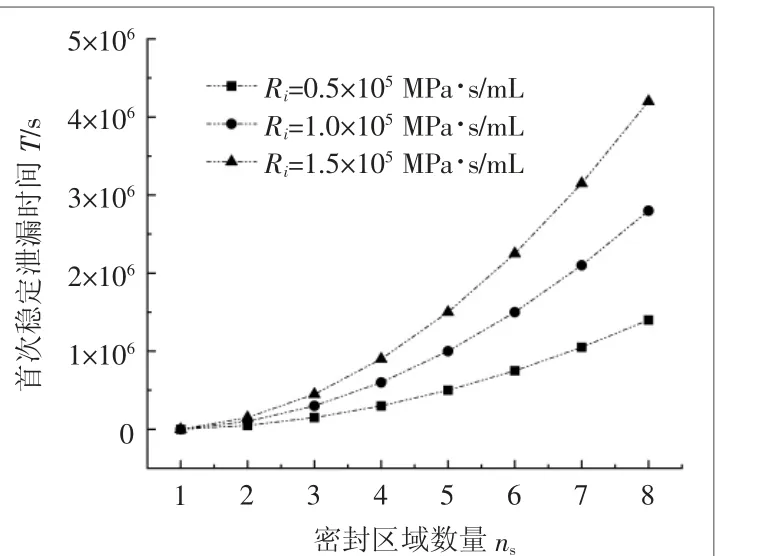
图6 密封区域流阻对首次发生稳定泄漏时间的影响
由图7可知,当多重静密封结构处于稳定泄漏状态时,密封区域数量ns越大,任一密封区域承担的压力差Δpi越小;密封区域流阻Ri对压力差Δpi无影响。

图7 密封区域数量对压力差分担作用的影响
2.2 总流阻相同条件下的泄漏特性分析
为进一步分析多重接触式静密封的泄漏特性,在总流阻相同情况下,调整密封区域数量和密封空间体积。给定密封区域数量ns=1~8,压力 差 为 1 MPa,总流阻R =10000 MPa ·s/mL,密封区域均采用相同流阻的密封单元,任一密封区域流阻为Ri=R/ns,密封空间体积Vci为10.0、15.0、20.0 mL。
由图8可知,当Vci=10.0 mL时,多重接触式静密封第i个密封空间充满液体的时间ti,随密封空间序号i增加而线性增大;当密封空间序号i相同时,密封区域数ns越大,第i个密封空间充满液体的时间ti越小,这是因为参与稳定泄漏的密封区域流阻总数较小,而压力差不变。

图8 密封区域数量对第i个密封区域首次稳定泄漏时间的影响
由图9可知,多重接触式静密封的密封区域数量ns越大,首次稳定泄漏时间T越大;当密封区域数量ns相同时,密封空间体积Vci越大,首次稳定泄漏时间T越大,这是因为在泄漏率相同的情况下,液体密封介质需要更多时间充满密封空间。
由以上分析可知,总流阻相同的多重接触式静密封,密封区域数量ns越大,密封空间体积Vci越大,发生稳定泄漏的时间T越大,密封性能越好。
3 结论
本文分析了多重接触式静密封的主要特征,建立了理论模型,通过数值仿真分析了密封区域数量、密封空间体积对泄漏特性的影响,主要得到了以下结论:1)通过增加多重接触式密封结构的密封区域数量,提高总流阻,有利于提高密封性能,获得更低的泄漏率。2)通过增加多重接触式密封结构的密封空间体积,可延长形成稳定泄漏时间,尤其适用于针对一些工况较为恶劣、工作时间较短的密封工况,在很难提高密封等级的情况下,增大密封空间体积,是一种较为经济的方法。3)在总流阻相同的情况下,可通过增加密封区域数量和密封空间体积,显著提高密封性能,尤其是适用于要求较高的密封条件。
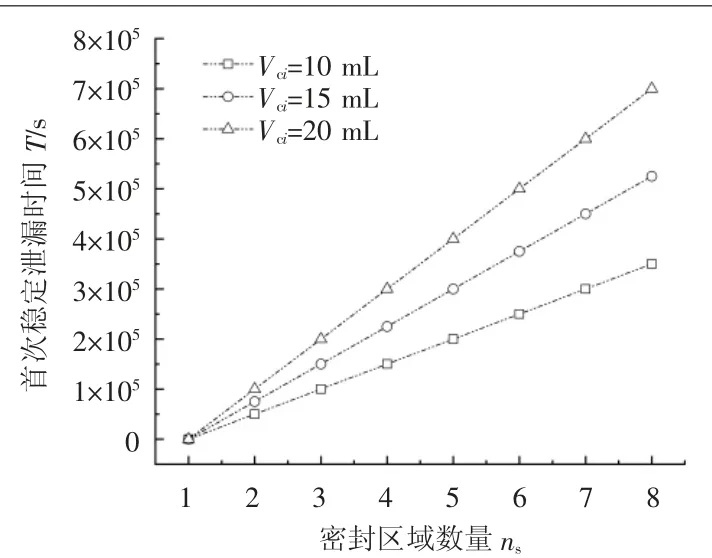
图9 密封空间体积对首次稳定泄漏时间的影响
该理论模型也同样适用于动密封和非接触式密封,在确定密封流阻的情况下,可以对多重密封进行结构设计,为密封性的定量分析提供了参考。
