一种新的地震危险性表达方法研究*
2022-12-21张萌潘华
张萌潘华
(中国北京 100081 中国地震局地球物理研究所)
引言
地震危险性分析是结构抗震设计、震害损失预测和抗震设防标准决策的重要依据,是工程抗震中最基础的工作.地震危险性是指某一场点在未来一段时期内可能遭遇的地震作用的大小和频次,它反映的是该场点面临的客观自然环境,即通常所说的地震环境,可用地震烈度或地震动参数来表示(胡聿贤,2006).地震危险性分析方法一般分为两种:确定性方法和概率性方法.由于地震发生的机制、传播路径和场地条件等环节都存在较强的不确定性,当前的科学水平还难以进行精确的预测,因此现在大多采用概率法进行地震危险性分析.
概率地震危险性分析综合了场点附近所有可能发生地震的构造和发生不同震级地震的可能性,给出该场点的地震动超过某一阈值的可能性,结果一般用超越概率表示.若假定地震事件在时间和空间上相互独立,即假定地震的发生是平稳泊松过程,则t年内地震动参数大于给定值a的超越概率为(Cornell,1968;McGuire,1976)

式中 λ (a)为地震动超越a的地震的年发生频率,可表示为

式中,vs为潜在震源区中地震的年平均发生率,f(rr|m)为m级地震的空间概率密度函数,fm(m)为震级m的概率密度函数.式(1)的计算结果为t年内场点地震动参数超越a的概率,针对一系列的值计算得到相应的Pe(xa)的离散数据点,表达了场点的地震危险性.通常将这一系列离散点绘制成连续的曲线,称为地震危险性曲线或超越概率曲线.通过地震危险性曲线可以得到所需要的不同超越概率下的地震动参数值,如地震动峰值加速度(peak ground acceleration,缩写为PGA),用于场地未来特定时段遭遇地震动大小的评价,或用于工程抗震设计与抗震分析.
地震危险性曲线可以完整地描述一个场点的地震危险性,然而一个场点用一组数据来描述过于繁琐,不便于实际的工程应用.当前国内外关于地震危险性曲线的应用,一般仅涉及地震危险性曲线上的个别点.例如, 《中国地震动参数区划图》(GB 18306——2015)(中华人民共和国国家质量监督检验检疫总局,中国国家标准化管理委员会,2016)(以下简称“五代图”)采用了50年超越概率10%的峰值加速度作为编图指标; 《建筑抗震设计规范》(GB 50011——2010)(中华人民共和国住房和城乡建设部,中华人民共和国国家质量监督检验检疫总局,2010)采用50年63%,10%,2%三个超越概率水平的地震动参数;美国2018版国家地震危险性区划图采用50年超越概率10%,5%,2%地震动参数(Petersenet al,2014);美国建筑抗震设计规范采用50年超越概率2%地震动参数作为设计地震动(FEMA,2009;ASCE,2010);欧洲地震危险性区划中给出的是50年超越概率10%对应的PGA (Giardiniet al,2014).
随着社会经济的发展和对地震风险防范意识的强化,对地震危险性的需求也急剧增加.在编制地震区划图时,开始考虑增加超越概率水平尤其是低超越概率水平,以适应更广泛的应用需求如地震保险等业务.随着基于性态的抗震设计理念的出现和发展(Bommer,Pinho,2006),对地震危险性考虑的灵活性与多样性导致对多概率水准的需求迅速增长;重大工程的抗震设计也对多概率水平的地震危险性表达提出需求,如核电站地震概率风险分析中往往要求提供年超越概率水平10−4甚至更低的地震动参数.现行地震区划图的单一超越概率水准的表达方式难以满足当前对多概率水准地震危险性的需求,因此,迫切需要寻找一种精度较高、概率水平范围较广并且方便应用的方式来表达地震危险性.
鉴于此,本文建议使用一种基于新函数形式拟合地震危险性曲线的“特征系数法”,从而达到比较完整而精准地表达地震危险性的目的.首先回顾现在常用的几种地震危险性曲线的拟合方式;随后使用“五代图”的地震活动性模型和地震动衰减关系对全国的地震危险性进行计算,根据得到的地震危险性曲线对新函数的拟合效果进行检验,并与极值函数的拟合效果进行对比;最后对该函数中表征危险性曲线形状的关键参数即“特征系数”k的物理意义进行讨论.
1 地震危险性曲线的拟合方式
由于离散的地震危险性数据过于繁琐不便于应用,而单一超越概率水准的地震动又无法满足各领域对地震危险性的需求,因此使用函数对地震危险性曲线进行拟合成为近年来一种比较流行的做法.主要的拟合方法有分段直线拟合和幂函数拟合(极值函数拟合).下面分别对这两种拟合方法进行简单介绍.
1.1 分段直线拟合
根据地震区划图上给出的单概率水平地震动参数,相当于地震危险性曲线上的一个点,用简单的比例系数由该基准点外推其它超越概率水平的地震动参数值,这也相当于对地震危险性曲线的一个简单的定量化表述.例如,我国“五代图”以50年超越概率10%的地震动作为基本地震动,其1/3为50年超越概率63%的多遇地震动,其1.6——2.3倍为50年超越概率2%的罕遇地震动,其2.7——3.2倍为年超越概率10−4的极罕遇地震动(高孟潭,2015),这相当于定量化给出了具有一定不确定性范围的地震危险性曲线.在《建筑抗震设计规范》(GB 50011——2010)中,以地震区划图给定的50年超越概率10%的峰值加速度作为设计基本地震动,其0.35倍为50年超越概率63%的多遇地震动加速度,而罕遇地震加速度与设计基本地震加速度比例在不同基本烈度分区不一样:在6度区(相应地震区划图0.05g分区)为2.5;7度区(0.10g分区)为 2.2;7度强区(0.15g分区)为2.1;8度区(0.20g分区)为 2.0;8度强区(0.30g分区)为1.7;9度区(0.40g分区)为1.55 (中华人民共和国住房和城乡建设部,中华人民共和国国家质量监督检验检疫总局,2010),这就相当于在不同地震动分区给出了不同的地震危险性曲线.
这一方法默认地震危险性曲线可以由多段线性的公式来表征,也即基准点与比例控制点之间的关系曲线是近似线性的,可由线性插值外推相应概率的地震动,即
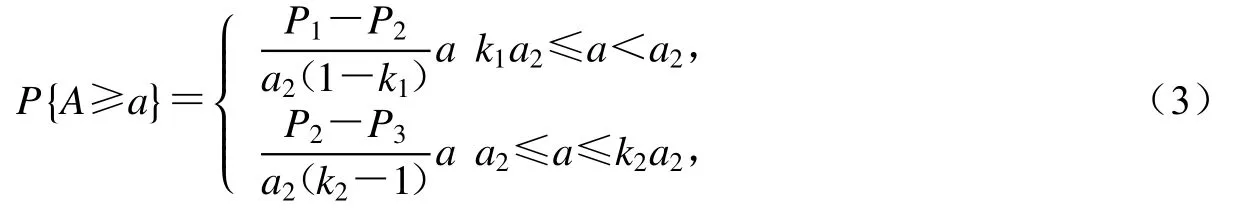
式中,P1,P2和P3分别为多遇地震动、基本地震动和罕遇地震动对应的超越概率,a1,a2和a3分别为多遇地震动、基本地震动和罕遇地震动的峰值加速度,k1和k2为比例系数.
这种方法在控制点上具有统计学意义,可以满足地震区划图或抗震设计规范这类重于面广、量大、关键点控制的相关应用的要求.但是现有的研究表明,这种按不同加速度分区乘以不同比例系数外推得到的设计地震动并不符合实际的危险性情况(高孟潭,卢寿德,2006).
1.2 幂函数拟合
Cornell (1968)最早从地震危险性分析的理想化模型中推断出年最大地震动峰值加速度服从极值Ⅱ型分布,则地震动的超越概率可以表示为

式中,k0和k为根据地震危险性曲线拟合得到的参数,其中k被称为特征系数或形状参数,它反映了地震危险性曲线的形状.
当超越概率较低时,Kennedy 和 Short (1994)给出了式(4)的近似表达式,即

该式认为地震危险性曲线服从幂函数形式.由于该拟合方法形式较为简单,因此得到了比较广泛的应用.Eurocode8 (European Committee for Standardization,2004)中推荐的地震危险性表达方法就是建立在幂函数基础上(Grantet al,2007;Crowleyet al,2009),即

式中a475为重现期475年的地震动,0.002 1=1/475即为重现期475年地震动对应的年超越概率.由式(6)可知,对于任意一个场点,若已知基本加速度a475和特征系数k,即可求出任意给定峰值加速度所对应的超越概率或重现期,也可以求出任意给定超越概率或重现期所对应的加速度.这种方法只通过两个参数即可将一条地震危险性曲线表达出来,极大地方便了地震危险性曲线的应用.
使用极值函数或幂函数拟合危险性曲线不失为一种很简便的方法,但是拟合的重现期范围非常有限.Kennedy和Short (1994)认为地震危险性曲线仅在超越概率水平相差10倍的两个点之间符合幂函数分布,例如年超越概率10−4——10−5区间内.基于极值Ⅱ型分布或幂函数拟合危险性曲线实质上都假设地震危险性曲线在双对数坐标下近似直线.
图1是使用式(6)对中国某城市PGA年超越概率曲线进行拟合的结果,其中计算值为实际地震危险性计算值.如果曲线符合极值Ⅱ型分布,那么在双对数坐标下计算点应近似呈直线分布,但从图中可以看出,实际的计算点并不符合直线关系.极值拟合精度较高的范围大约在年超越概率 2×10−2——10−3,即重现期50——1 000年之间,而且在该有效范围内危险性曲线也并不是严格的直线分布.这种在一定重现期范围内进行拟合的方法可以满足某种特定目标的抗震设计需求,但在较广范围内整个超越概率曲线并非近似意义上的直线分布,因此这种拟合方法是一种比较粗略的估计.
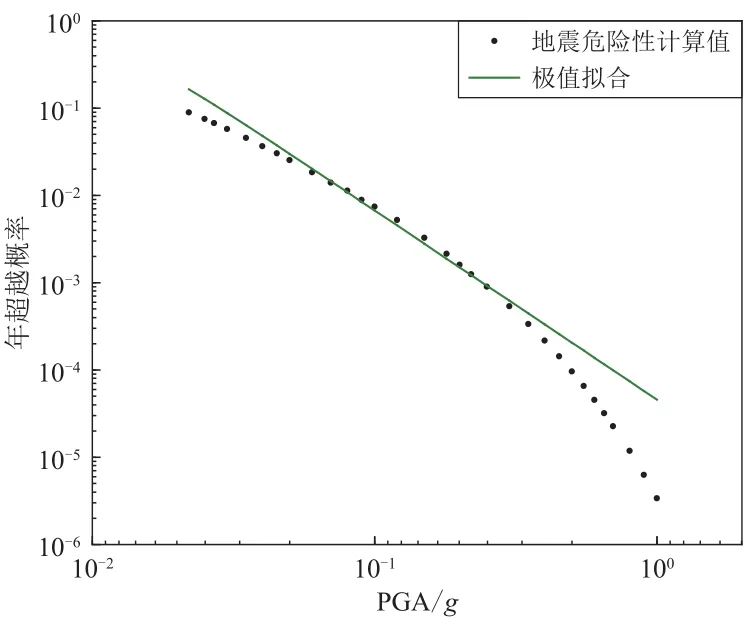
图1 某城市 PGA 危险性曲线与极值函数的拟合Fig.1 Results of the PGA hazard curve fitting the extreme value function for a city
2 特征系数表达方法
由图1可知,随着超越概率水平的逐渐降低,曲线逐渐出现了收敛的趋势,即斜率越来越大.这主要是由于断层的发震能力有限,体现在参与危险性计算的潜在震源区都有一个震级上限.结合地震动衰减关系可知,在距断层某一距离产生的地震动不可能无限大,所以得到的危险性曲线将在低超越概率段出现收敛的趋势.因此,对危险性曲线的拟合须基于一种非线性函数,以便准确地反应实际的曲线形状.{}
假设地震危险性曲线在双对数坐标中满足指数分布,即 lnPA≥a和 lna应满足


式(8)即为本文给出的拟合地震危险性曲线的新函数形式,其中k0和k1根据地震危险性曲线拟合得到.由式(8)拟合的和 lna的结果见图2.对比图1和图2可以看出,指数拟合在拟合效果上有了明显的提升,拟合精度较高的范围大约在年超越概率 4×10−2——2×10−5,即重现期 25 年到5万年.

图2 某城市 PGA 危险性曲线与新函数的拟合Fig.2 Results of the PGA hazard curve fitting the new function for a city
为了便于该函数形式在实际中的应用并与现行的“五代图”更好地进行衔接,将式(8)转化为

式中, P GA475为“五代图”给出的50年超越概率10% (重现期475年)对应的峰值加速度,k反映了危险性曲线的形状,在本文中被称为“特征系数”.与基于极值Ⅱ型函数拟合[ 式 (6)] 类 似,指数函数拟合[ 式 (9)] 也 是由两个参数即一个分位数PGA475和一个特征系数k来控制.与之不同的是,这种形式可以将 lnP和 lna在双对数坐标下表现为指数形式而非直线形式,更符合实际的危险性曲线,从而提高危险性曲线拟合的精度.
3 实例分析
为了检验本文给出的新函数拟合危险性曲线的效果,计算了我国大陆地区0.2°×0.2°间隔的2万4 043个网格场点的基岩处的PGA危险性曲线,在概率危险性计算时采用了为“五代图”建立的潜在震源区方案(周本刚等,2013)、地震活动性模型(潘华等,2013)和地震动衰减关系(俞言祥等,2013).使用式(9)对每个场点的地震危险性曲线进行拟合,其中特征系数k根据最小二乘法确定.图3表明所有2万4 043个计算场点的特征系数k的范围为0.18——0.55,主要集中在0.3——0.4之间,并且近似服从均值为0.34的正态分布.
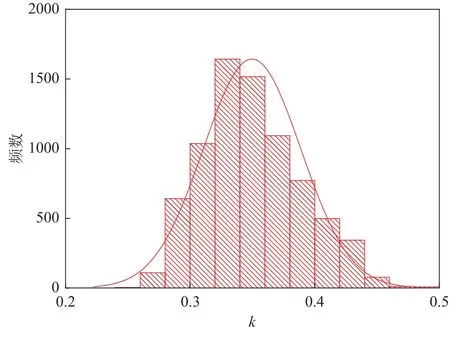
图3 全国 0.2°×0.2°间隔 2 万 4 043 个场点特征系数k的频数分布Fig.3 Distribution of the frequency of the characteristic coefficient k for the national 24 043 sites with interval of 0.2°×0.2°
为了更直观地评价特征系数法的拟合效果,定义了相对残差Res来反映在某一超越概率水平处的拟合效果,即

式中, P GAfit和 P GAcal分别为PGA的拟合值和计算值.相对残差 R es越小说明在这个超越概率水平的拟合效果越好,反之则越差.
图4给出了特征系数法拟合方法在5个超越概率水平(50年63%,50年10%,50年5%,50年2%和50年0.5%)下的相对残差Res分布.从图中可以看出,相对残差 R es在10%以下的点分别占所有场点数量80%以上,在3个低超越概率水平段(50年5%,50年2%和50年0.5%)更是几乎全部场点都在10%以下;而相对残差Res在5%以下的点基本占所有场点一半以上,在3个低超越概率水平段(50年5%,50年2%和50年0.5%)相对误差在5%以下的点都占所有场点数量90%以上.因此可以认为特征系数法拟合地震危险性曲线的效果良好,能比较完整地描绘地震危险性曲线.
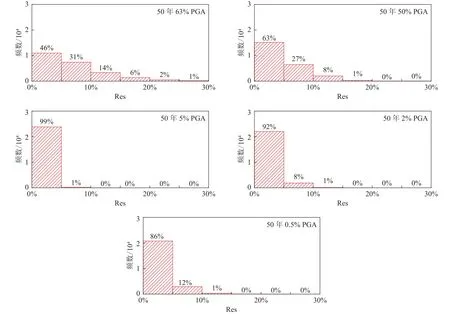
图4 特征系数法的拟合残差 Res统计对比Fig.4 Statistical comparison of fitting residuals for shape parameter method at 24 043 sites
表1和图5给出了我国四个城市(北京、上海、兰州和成都)使用特征系数法拟合PGA危险性曲线的结果.从表1中可以看出,这四个城市在给定的超越概率水平处计算值与拟合值相差不大,拟合的相对残差 R es几乎都在5%以下;从图5中可以看出拟合曲线与实际的计算值十分接近,拟合精度较高的范围约在年超越概率5×10−2——10−4(重现期20年——1万年).这个拟合范围不仅涵盖了我国抗震设计规范中提出的三级设防水准,甚至可以满足“五代图”中提出的年超越概率10−4即万年一遇的极罕遇地震动.

表1 4个城市特征系数法拟合的地震危险性曲线相对残差Res结果Table 1 Fitting results of the relative residuals for seismic hazard curves by the characteristic coefficient method for four cities
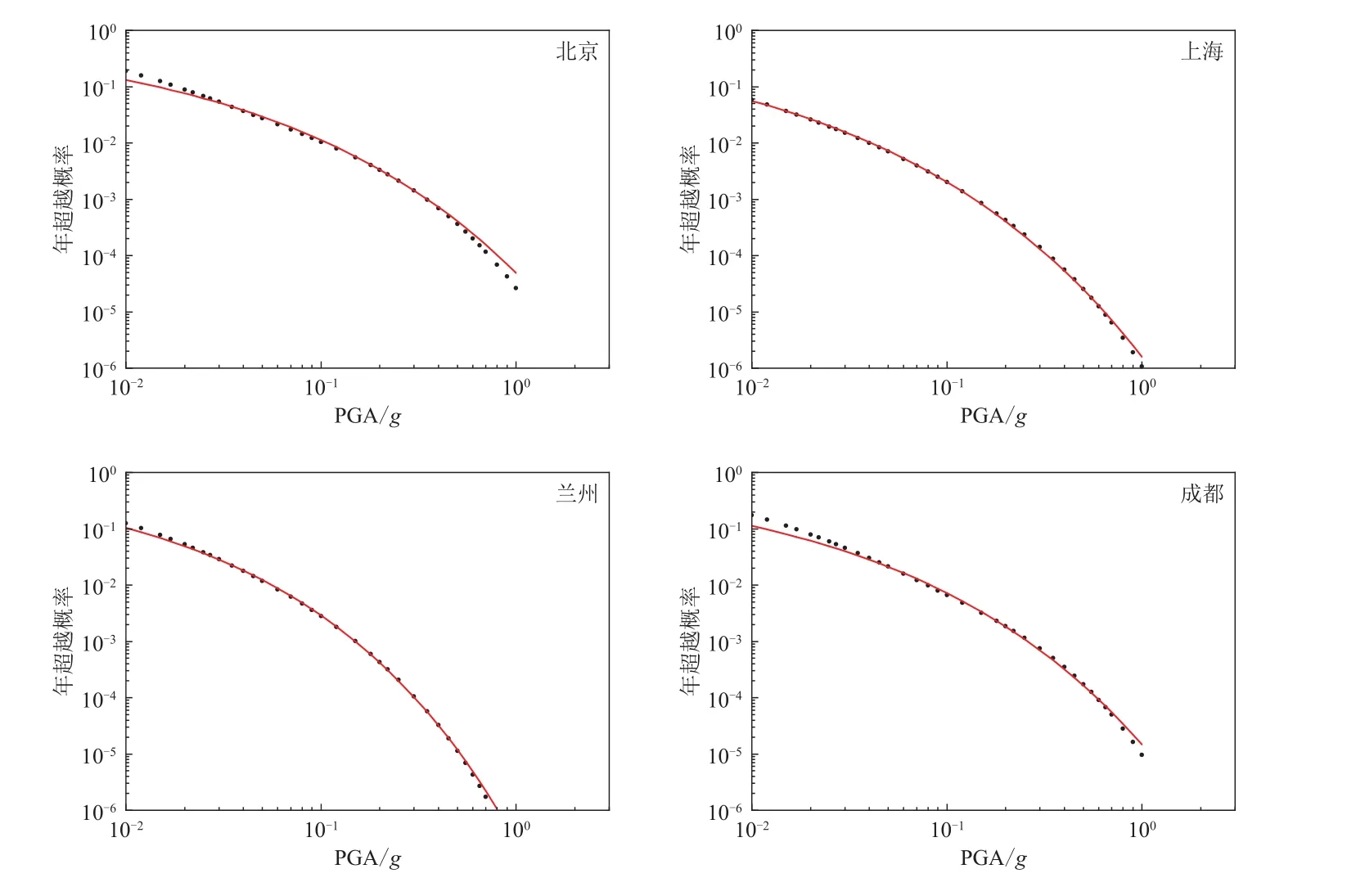
图5 四个城市基于特征系数法拟合得到的地震危险性曲线Fig.5 Seismic hazard curves based on the characteristic coefficient method for the four cities
除PGA之外,本文还用式(9)对其它反应谱周期点的谱加速度危险性曲线进行了拟合.图6给出了某城市在4个反应谱周期点(0.01,0.2,1,4 s)谱加速度危险性曲线的拟合结果,可以看出在这几个周期点拟合效果良好.

图6 某城市基于特征系数法的谱加速度危险性曲线拟合结果Fig.6 Results of fitting for the spectral acceleration hazard curve of a city based on the characteristic coefficient method
4 特征系数k与地震环境关系分析
一般来说,地震危险性曲线的形状在一定程度上反映了这个地区的地震环境或地震活动性的强弱.例如,通过对美国部分城市地震危险性结果的分析,认为在地震活动性较强的城市如洛杉矶,PGA2 475与PGA475的比值为1.7,明显低于地震活动性较弱的中部城市孟菲斯的5.1 (James,2002);在对中国第五代区划图进行的相关统计中(高孟潭,2015)对中国大陆地区经纬度间隔0.1°×0.1°的约10万个场点进行统计分析发现,PGA2 475与PGA475的比值在不同加速度分区之间基本保持一致,大约在1.9左右,并无加速度分区差异.这些研究均认为地震危险性曲线的形状仅与单一概率水准PGA有关,而我们认为地震环境是一个比较复杂的概念,很难用单一的PGA来表征.本文试图以特征系数k值表征危险性曲线形状来讨论不同地震危险性曲线的形状与地震环境的关系.
本文选择使用分解法来展示不同场点面临的地震环境(McGuire,1976),从而寻找它与特征系数k值的关系.通过将某一场点特定的超越概率水平的PGA按距离进行分解,可以得到不同距离段对该PGA的贡献.下面选取超越概率曲线形状(k值)差别较大而基本设防烈度PGA475较为接近的两个城市,拉萨和常德,进行具体的分析.
拉萨和常德的特征系数k分别为0.45和0.27,其对应的PGA475分别为0.17g和0.18g,相差仅0.01g,而PGA2 475分别为0.29g和0.42g,相差将近0.13g.两个场点的PGA475较为接近,但是PGA50和PGA2 475却相差比较大.图7给出了两个场点的PGA危险性曲线,可明显看出两个场点的危险性曲线的形状存在显著差异,拉萨场点k值较大,所以超越概率曲线比常德下降地更快.
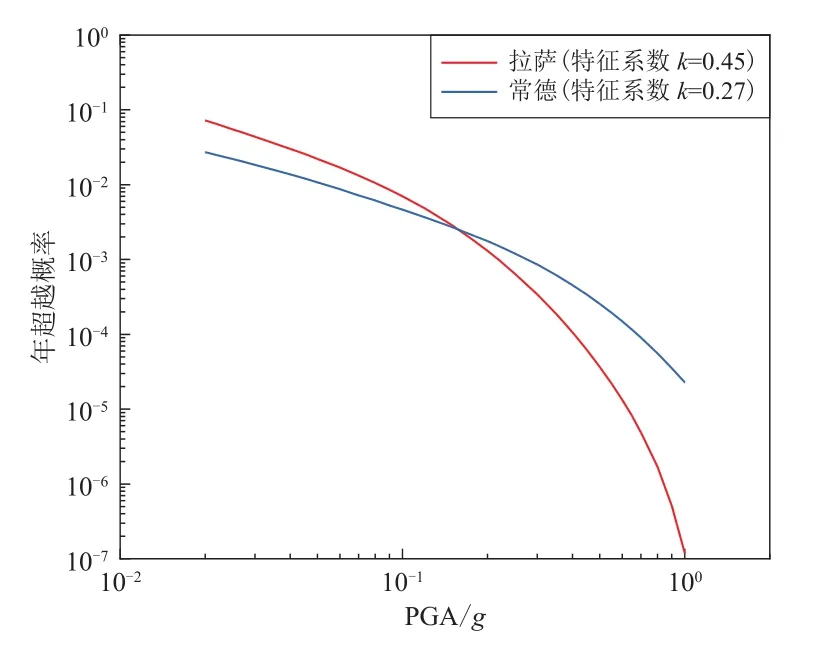
图7 拉萨和常德两场点 PGA 年超越概率曲线对比Fig.7 Comparison of the annual PGA exceedance probability curves for the two sites in Lhasa and Changde
图8给出了拉萨和常德按不同距离贡献分解PGA475和PGA2 475的结果.从图中可以看出:① 对同一场点来说,不同超越概率水平下PGA按距离分解的曲线形状差别不大,基本趋于一致.如对拉萨的PGA475和PGA2 475贡献主要来自40 km以外中远距离的潜源,在近场40 km以内只有很小部分贡献;而常德PGA475和PGA2 475的贡献则主要来自近场30 km以内的潜源,基本不受30 km之外的潜源影响.因此可以认为影响拉萨PGA曲线的因素主要为远场潜源,而影响常德PGA曲线的因素则主要为近距离潜源.② 对不同场点来说,对危险性贡献的主要距离与表征危险性曲线形状的参数即特征系数k有关.对k值较高(0.45)的场点拉萨来说,对危险性曲线的贡献主要来自远距离,而对k值较低(0.27)的常德来说,对危险性曲线的贡献主要来自近场的潜源.也就是说,k值较高的场点周围近距离地震活动性较弱,而远距离地震活动性较强;而k值较低的场点预示着场点近距离范围内应该有较强地震活动性的潜源.

图8 拉萨和常德两场点PGA危险性曲线分解结果对比横坐标表示计算时离散化微元到场点的距离,纵坐标代表不同距离微元贡献的百分比即概率密度函数PDF(a) 50 年超越概率 10% 的 PGA;(b) 50 年超越概率 2% 的 PGAFig.8 Comparison of the results of the PGA hazard curve decomposition at the Lhasa and Changde sitesThe horizontal coordinate represents the distance from the discretized microelements to the field point at the time of calculation,and the vertical coordinate represents the percentage of contribution from microelements at different distances, that is,the probability density function PDF(a) PGA for 10% probability being exceeded in 50 years; (b)PGA for 2% probability being exceeded in 50 years
这一结论与图9所示的拉萨和常德周边的“五代图”潜在震源区分布情况一致.在拉萨周边近场30 km内无潜在震源区,最近的一个潜源(1406号)在50 km之外,因此拉萨场点的地震危险性主要来自远场约50 km之外活动性较强的潜源;而反观另一个场点常德,本身处在一个较强的M7.0震源区内,附近200 km范围内再无活动性较强的潜在震源区,因此远处的潜源几乎没有贡献,该场点地震危险性主要来自近场较强的潜源.

图9 拉萨和常德两场点潜在震源区分布Fig.9 Distribution of potential source areas at the sites of Lhasa and Changde
为了进一步验证上述结论,我们选取了中国大陆地区特征系数k值较高和较低的两组共计32个场点并分别对PGA475和PGA2 475按不同距离潜源的贡献进行了分解.为了更直观地衡量对场点危险性起主要影响的距离,对每个场点分别计算出与PGA475和PGA2 475对应的贡献的期望距离,结果分别列于表2和表3.
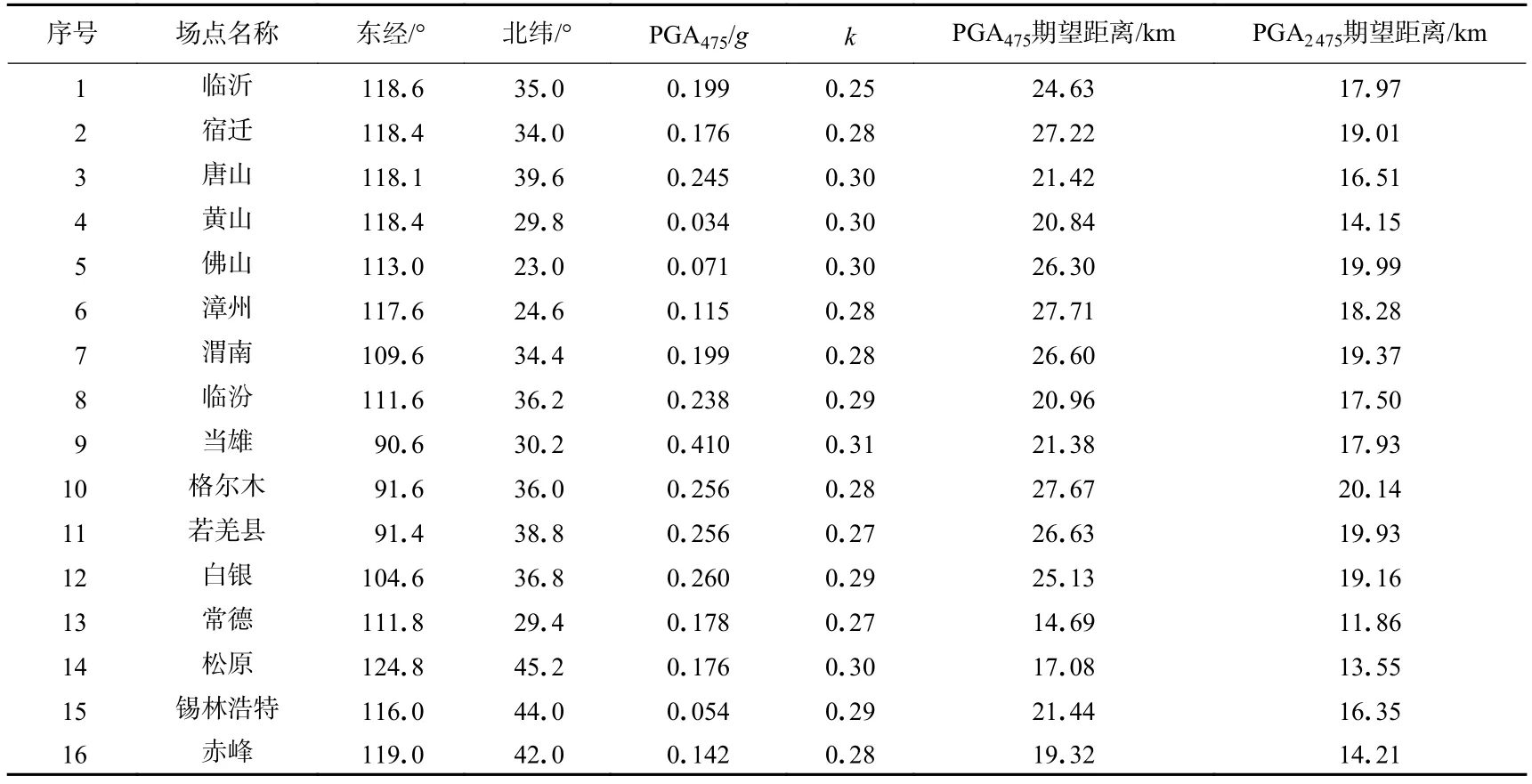
表2 低 k 值场点期望距离计算结果Table 2 Calculated expected distances for low k-value sites

表3 高 k 值场点期望距离计算结果Table 3 Calculated expected distances for high k-value sites
表2列出的16个场点k值基本都在0.3以下,属于k值偏低的地区,PGA475对应的期望距离在20——30 km之间,最大的是漳州的27.71 km,PGA2 475对应的期望距离基本不超过20 km,可以认为对这些场点危险性起作用的潜源主要来自近距离;表3列出的16个场点的k值基本都在0.4以上,属于k值偏高的地区,而PGA475对应的期望距离在40——60 km之间,PGA2 475期望距离在35——50 km之间,与低k值组对比,可以认为对这组场点危险性有贡献的潜源主要来自中远距离.
上述结果说明,具有较低k值的场点危险性主要来自场点附近的潜源,表明该场点很可能位于周边相对较强的潜在震源区内;而对具有较高k值的场点的贡献则不仅依赖于近场,在整个有影响的距离范围内的潜源都有贡献,这表明该场点应该是处于较强的潜在震源区之外一段距离或者在周边相对较弱的潜源内部.
5 讨论与结论
本文采用一种新的函数形式拟合地震危险性曲线,该函数只需PGA475和反映曲线形状的特征系数k两个参数即可表征.使用“五代图”基础资料计算了全国2万4 043个场点的地震危险性曲线用以对该函数的拟合效果进行检验,结果表明该函数能够在较广的重现期范围内精确地描述地震危险性曲线,是一种简便且精准的表达地震危险性的方法.另外,通过将特定超越概率水平的地震动按不同距离进行分解,探讨了特征系数k与地震环境之间的关系.结果表明,危险性曲线形状或特征系数k与危险性的贡献距离有关,k值较低的场点危险性贡献基本来自近场,而k值较高的场点中远距离的贡献是不能忽视的.
与分段直线拟合和极值函数(幂函数)拟合相比,使用本文给出的新函数拟合地震危险性曲线在精度和范围上都有明显的提升,是一种更好的地震危险性表达方法.在对地震危险性精度要求日益增长的情况下,本文提出的特征系数法能够较为完整地表达地震危险性信息,从而使地震区划图的应用前景得到一定的扩展,能够更好地满足基于性能的抗震设计、地震风险评估、巨灾保险等相关领域对详细地震危险性信息的需求.
本文的研究认为具有较低k值的场点处于周边环境中地震活动性相对较强的位置,而具有较高k值的场点处于周边环境中地震活动性相对较弱的位置.也就是说在一定区域内地震活动性相对较强的地区,k值会较周边地区明显偏高.这表明在未来如果采用以k值分区形式进行地震区划工作,应着重注意在区域范围内的较高震级潜在震源区内部的场点,这些场点在不同超越概率水平下的比值比周边地区偏高.
在未来的工作中,除了选择适当的地震动参数(例如50年超越概率10%的PGA)之外,还需要对特征系数k的合理分区进行讨论以便应用到地震区划中.
