管路结构振动控制技术研究及仿真分析

2022-12-20郑奇辉

机电产品开发与创新 2022年6期

吴斌，邓琎，郑奇辉

（1.中国船舶集团有限公司第705 研究所，云南昆明 650101；2.云南省机械研究设计院有限公司云南省机电一体化应用技术重点实验室，云南昆明 650031）

0 引言

管路内的流体在流动过程中，由于受到压力改变、管路弯头、管径变化等因素的影响导致流速变化，由此产生了管路结构振动。

管路系统的振动问题又被称为“典型动力学问题（a modal dynamical problem）”，自19 世纪以来，针对管道流固耦合振动的研究已经获得了长足的发展。流体输送大多采用泵作为动力原件，由于泵送流体的不恒定，会产生管内流体压力脉动，进而诱发较为强烈的耦合振动，通常会引起辐射噪声、管路系统振动和疲劳破坏等[1-3]。在先进国家，每年由于管路振动所带来的经济损失也是巨大的，据一位加拿大专家估计，工业先进的美国，过去因为管路振动而造成的损失，每年达100 亿美元以上[4-5]。所以，降低管路系统振动，保证管路安全工作，具有很高的理论研究价值和重大的现实意义。

考核物体的振动强度大小通常有三个标准[6]：位移、速度和加速度。振动位移表示振动幅度的大小，振动速度表示振动能量的大小，振动加速度则表示了冲击力的大小。本文对于管路系统振动控制的效果主要通过位移、速度进行衡量与评价的，主要采取改变管路结构的形状以及改变管路系统结构特性来达到抑制管路结构振动。

1 改变管路系统的形状

管路参数如下：不锈钢管材料为1Cr14Ni2，管外径为0.038m，壁厚0.004m，长度为4m，弹性模量为E=2.0×1011N/m2，泊松比为ν=0.3，密度为ρ=7800kg/m3，边界条件为两端刚性连接[7-8]。

进行网格划分后生成的有限元模型如图1～4 所示。

图1 管路的有限元模型Fig.1 Finite element model of pipeline

图3 变形后管路的有限元模型Fig.3 Finite element model of deformed pipeline

图1 为管路未改变形状之前时的有限元模型，图2是改变管路形状后的有限元模型，图1、图2 中有限元模型是在不改变管路本身的质量，以及管路的连接方式，仅改变其形状条件下仿真计算的。从图2 与图4 可以看出，未改变管路形状前，其在一阶模态下的节点位移的最大值为0.310296m，变形后管路一阶模态下的节点位移最大为0.296576m，与未改变管路形状之前相比，其节点位移最大值降低了0.01372m，下降了约4.4%。再者可以发现，对于两端刚性连接的管路，其在一阶模态下节点位移的最大值一般出现在管路的中间部位。从有限元分析当中可以得出，在管路不改变其本身质量，不改变管路连接方式的条件下，仅仅改变管路的形状也可以降低管路结构的振动幅度，以此来达到抑制管路结构的振动。

图2 管路的一阶模态下节点位移图Fig.2 The nodal displacement of pipeline in first order mode

图4 变形后管路一阶模态下节点位移图Fig.4 Displacement of joints in first-order mode after deformation

根据弯管的有限元模型及参数，可以计算得到弯管未变形时5 阶固有频率，见表1 及变形后的5 阶固有频率，见表2。

表1 未变形后的固有频率Tab.1 The natural frequency without deformation

表2 变形后的固有频率Tab.2 The natural frequency after deformation

从表1、表2 以及图5 可以看出，在不改变管路本身质量，不改变管路连接方式的条件下，如果管路的形状发生了变化，管路的固有频率随之也会发生变化。变形前后管路的固有频率相比，前五阶固有频率都比变形前小，其中改变形状后管路第一阶固有频率与之前相比降低了约4.62%，第二阶固有频率降了27.1%，第三阶固有频率降低了15.9%，第四阶固有频率降低了40.4%，第五阶固有频率降低了20.8%。因此，可通过改变管路的形状，来改变管路的固有频率。这样以来，可很好的避开共振频段，防止发生共振，以此来提高管路系统工作的可靠性，对管路的安全起到了一定的作用。

图5 固有频率柱状比较图Fig.5 Histogram comparison of natural frequencies

综上分析，在不改变管路本身质量，不改变管路连接方式的条件下，改变管路的形状，即可改变管路的一阶模态下节点位移振动幅度，以及管路的固有频率，进而可以达到抑制管路振动目的，避开管路系统的共振频段，使得管路系统安全可靠的工作。

2 改变管路系统振动特性

对于管路系统而言，要抑制其振动噪声，最有效最直接的方法是抑制管路的振源（即消除激扰力），然而消除振源对投入使用中的管路系统来说，代价很大，因此需采取其它措施来抑制管路的振动，将振动响应控制在一定范围内。

管路系统结构运动微分方程可表示为[9-10]：

式中：M、C 和K∈Rn×n—管路结构质量矩阵、阻尼矩阵以及刚度矩阵；X（t）∈Rn—管路结构的位移向量；X··∈Rn、X·∈Rn—管路结构质点的振动加速度、振动速度；X（t0）、X·（t0）∈Rn—管路结构的初始位移向量和初始速度向量；F（t）—管路结构所受到的激扰力列向量，激扰力包括机械振动、流体振动和地震激扰力。

从上式可得出，管路结构的质量矩阵、阻尼矩阵和刚度矩阵三个向量是表示管路结构特征重要指标。因此，对管路结构的振动控制应当着眼于提高管路结构的刚度，增加阻尼，改变结构质量几个方面，从而起到抑制管路结构的振动的作用。

通过以上的分析可知，改变管路结构的质量矩阵主要是通过改变管路的壁厚，这就需要替换管线形式，代价太高，另外工况确定后，很难显著改变管路结构的阻尼矩阵。因此通过合理改变管路的长度，即增加管路的约束，可降低管路结构的振动。这种方法在原有基础上，施工改造相对容易，经济性好。

为了检验改变管路的长度对振动抑制效果，为此进行了仿真分析，对不同长度的管路的进行仿真，以此来验证，管路的长度相对较短时，结构的振动相对较小，即增加管路的约束，以此来增加管路的强度，进而使得管路的振动得到抑制。但不是管路的长度越小越好，约束的越多越好。过度的对管路施加约束，从表面现象来看，该段管路的结构振动幅度确实在减小，但激振力仍然在不断的冲击着管路，由于该段管路所蕴含的波动能量无法得到有效的释放，前面的振动波和后面的振动波相互叠加，这样会加剧管路的振动，从而导致管路系统中原来不振动的部分开始振动。

图6 到图7 为管路长度分别为1、2、4、8、12m 时前二阶模态下的节点位移云图（管路受到10MPa 激励）。

从图6 中可以看出，在一阶模态下，管路长度为1m 时，其振动时的最大位移幅度为0.593066m，长度为2m 时，振动最大位移为0.423689m，长度为4m 时，振动最大位移为0.300484m，长度为8m 时，振动最大位移为，0.212639m，长度为12m，振动最大位移为0.173644m，因此，在一阶模态下，管路长度为1m 时的振动位移最大。从图6 以及图7中可以看出，不管是在一阶模态下，还是在二阶模态下，管路长度为1m 时的振动位移最大，长度为2m 的次之，管路长度为12m 时的振动位移最小，这说明在共振条件下，管路的长度越短，其振动的位移就相对越大。这就要求对于一些相对长度较短的管路系统，要尽量防止其发生共振，降低管路的结构振动噪声，这样不仅提高了管路自身工作的可靠性以及安全性，也可提高船只的隐蔽性以及生存能力（对于船只管路系统而言），降低管路系统的结构振动，对于设备的减振降噪具有重要意义。

图6 第一阶模态下的节点位移云图Fig.6 Nodal displacement cloud image in the first mode

图7 第二阶模态下的节点位移云图Fig.7 Nodal displacement cloud image in the second mode

从图8 可以看出，管长为1m 的管路，其固有频率比其他长度（2、4、8、12m）管路同阶次的固有频率要高，长度为12m 的管路要比其他长度的管路同阶次的固有频率相比，其值为最小。从仿真的结果来看，要提高管路的固有频率，管路的系统的长度就要选用相对较短的，这样以来，就可以避开系统的共振区域，使得管路不容易发生共振。如果要降低管路系统的固有频率，则应该适当增加管路的系统的长度。这样为管路的系统的振动控制提供一种方法，此方法可以使得管路系统不会发生共振，以便管路系统稳定的工作。

图8 不同长度管路的固有频率比较图Fig.8 Comparison of natural frequencies of pipelines of different lengths

图9 为位移响应峰值比较图。从图9 可以看出长度为1m 的管路的振动幅度的峰值最小，其幅度峰值为1.38×10-6m，长度为2m 的管路振动幅度次之，其振动幅度峰值为1.62×10-6m，长度为4m 的管路的振动幅度峰值为1.71×10-6m，长度为8m 的管路振动幅度峰值为1.75×10-6m，长度为12m 的管路的振动幅度峰值最大，其振动幅度为1.79×10-6m。因此对于相同管径、相同材料以及相同的约束方式等条件下管路系统而言，当受到相同的激振力的作用下，长度相对较短的管路振动幅度峰值相对较小，长度相对较长的管路，其振动幅度峰值相对较大。由以上分析可知，要降低管路系统的振动幅度，以达到降低结构的振动，可以采取缩短管路系统的长度（在条件允许的情况下），即在较长管路系统当中，施加一定的约束，这也相当于将一根较长的管路，分成几段，每根管路的长度相对原来的管路系统而言，长度缩短了，其结构振动也就得到了有效的抑制。

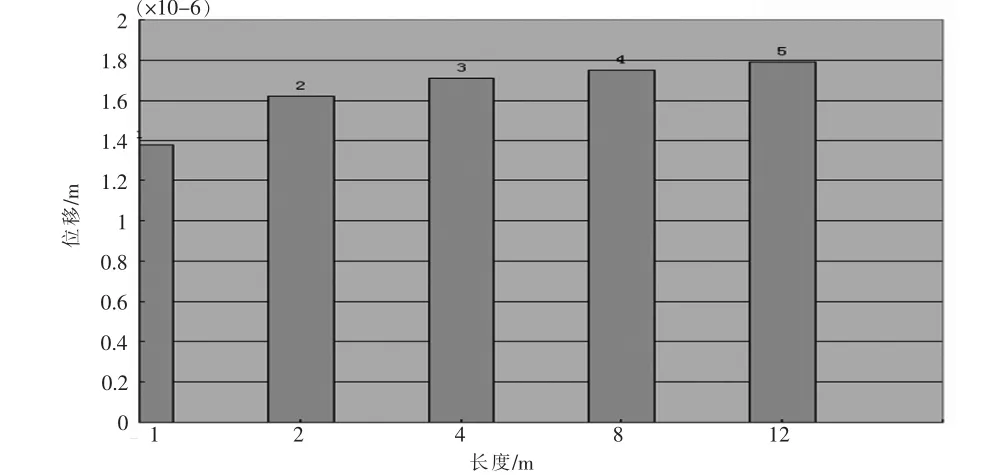
图9 位移峰值比较Fig.9 Comparison of displacement peaks

图10 是不同长度（1、2、4、8、12m）管路在8MPa 激振力的作用下振动加速度响应曲线图，从图中可以看出，管路长度为1m 时，振动加速度的峰值为56.3m/s2，长度为2m时，振动加速度的峰值为33.2m/s2，长度为4m 时，振动加速度的峰值为11.9m/s2，长度为8m 时，振动加速度的峰值为5.7m/s2，长度为12m 时，振动加速度的峰值为3.15m/s2。管路长度为1m 时，振动加速度的峰值最大，长度为12m时，振动加速度的峰值最小，由于振动加速度代表着冲击力的大小，这也说明管路长度为1m 时，冲击力振动最为剧烈。且在相同振动条件下，随着长度的增加，振动加速度的峰值呈现出递减的趋势。

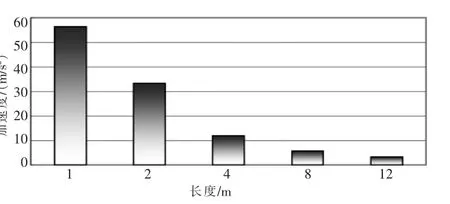
图10 不同长度管路振动加速度峰值比较图Fig.10 Comparison of vibration acceleration peaks of pipelines of different lengths

从振动速度响应曲线图11 可以看出，管路长度为1m 时（受到的激振力均为8MPa），振动速度的峰值为1.18m/s，长度为2m 时，振动速度的峰值为5.25m/s，长度为4m 时，振动速度的峰值为3.18m/s，长度为8m 时，振动速度的峰值为1.98m/s，长度为12m 时，振动速度的峰值为1.32m/s，其中管路长度为1m 时，振动速度的峰值最小，长度为2m 时，振动速度的峰值最大，长度为4m 的次之，再者为8m 时的振动速度峰值，其次为12m 的振动速度的峰值。从以上的分析可以看出，振动速度的峰值的大小，与管路的长度没有必然的联系，管路长度的增加，振动速度的峰值并没有呈现出一致的增加或者减小，管路长度的缩减，振动速度的峰值也没有发生有规律的变化，整个趋势未呈现出一定的统计性，无法得出一定的趋势规律，对后续长度管路的振动速度的峰值的趋势无法进行预测。

图11 速度响应曲线Fig.11 Velocity-response curve

结构振动噪声的辐射效率σ 的定义：由结构振动引起的噪声辐射到半球空间的声功率与相同表面积和均方振动速度的辐射所产生功率的比值，反映了结构表面振动转化为外声场噪声辐射的能力。对于结构噪声辐射，当频率为f 时，结构声辐射的声功率Wrad（f）同辐射面积Srad和均方速度值＜U0（f）2＞之间的关系可用下式来表示[11]：

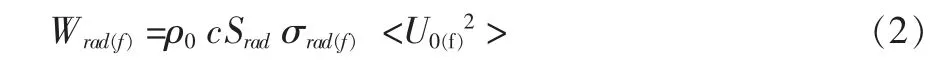
根据加速度谱，可知辐射声功率与部件的振动速度有关。为了更直观地反映结构振动与辐射噪声两者之间的关系，先测量加速度，再由辛普森积分方法将振动加速度转化为振动速度。式中：空气声和结构声基准速度的性质同空气中平面波的声强级（声压级和振动速度级一样。参考标准通常取uref=5×10-8m/s）。

结构噪声辐射的声功率级为[12]：

式中：ρ0c、S 都是已知量，＜ν2＞可以通过结构表面振动试验测量得到，Δ 为A 计权网络的衰减量，辐射效率σ，Wref为参考声功率，取10-12w。

结构声的辐射效率与结构表面振动速度均方值有关，振动速度体现振动能量的大小，要降低结构噪声，归根到底就是要降低结构的振动能量。因此降低管路系统的结构振动是降低管路系统结构振动噪声的有效手段。

在国际标准中选用振动速度作为衡量振动激烈程度的参考量，这是由于振动速度可以充分体现振动能量大小，大部分机器机械设备结构的失效，都是由于振动的速度过大而引起的，机械设备的结构噪声与振动的速度成正比例关系。

振动烈度是指物体振动速度的均方根值。它包含各阶次谐波能量的总振动能量的大小。

振动烈度计算公式[13-14]：

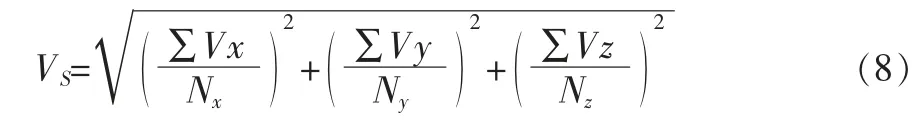
式中：VS为振动烈度（m/s），Vx、Vy、Vz 分别为x、y、z 三个方向上振动速度的有效值（m/s），Nx、Ny、Nz分别为x、y、z三个方向上的测试点的数量。

振动速度反映的是振动能量的大小，结构振动噪声传递其实归根到底还是振动能量传递，它是振动能量的一种形式，因此振动速度的有效值可以衡量振动抑制的效果。

通过仿真计算结果可以看出，长度为1m 的管路的振动速度的有效值最小，即振动程度最为不剧烈，依次从小到大为2m，4m，8m 的振动速度的有效值，长度为12m 的管路振动程度最为剧烈。长度为1m 的管路结构振动最小，长度为12m 的管路的振动最大，这说明对于管路系统施加约束的方法（间接增大管路刚度，改变了刚度矩阵），对于抑制管路结构的振动是行之有效的。

因此可以通过改变管路系统振动特性，来达到抑制管路系统的结构振动以及结构振动辐射噪声。