城市轨道交通地面线环境振动衰减规律分析
2022-12-20张伯林张宏亮董振升李文英
张伯林,陈 鹏,裴 欢,张宏亮,董振升,李文英
(1.南京地铁集团有限公司,南京 210008;2.北京城建设计发展集团股份有限公司 北京市轨道结构工程技术研究中心,北京 100037;3.中国铁道科学研究院集团有限公司 铁道建筑研究所,北京 100081)
地铁列车运营产生的振动波传递特性主要涉及振动波传播范围、衰减梯度及频率特性等,其因轨道交通的敷设方式、地质情况等的不同而存在很大的差异[1]。早在20 世纪80 年代,茅玉泉[2]通过大量实测研究铁路列车和地面交通在运行过程中引起的地面振动特性和衰减,提出了振动衰减的经验公式。杨先健等[3-4]基于理论同时考虑瑞利波和体波的影响,提出了动力机械的地面振动衰减公式,并将该公式纳入《动力机械基础设计规范》中。闫维明等[5-7]对不同地铁线路段,包括直线段、曲线段、车辆段,进行了大量的现场测试与分析。由于水平距离、埋深、地质条件等因素的差异,地面振动响应量值和频率分布也不同。总体上,地面振动响应频率成分在50 Hz~80 Hz占优势。
虽然对轨道交通引起的环境振动已经有了大量的研究[8-14],但针对轨道交通地面线路引起环境振动的研究很少。随着敏感建筑邻近车辆段(停车场)出入段、试车线或城际快线、市郊铁路等地面线路的情况大量出现,对于地面线路所致振动传递特性和环境振动影响研究越来越迫切。为了探索地面线路所致环境振动的传递特性,以城市轨道交通地面线距线路中心100 m 范围内自由开阔场地为研究区域,从时域与频域的角度分析地面线路振动波传播机理。
1 地面振动传递的复合回归方法
1.1 轨道交通振动传递规律
轨道交通钢轨-车轮接触面处产生的轮轨作用力以振动波的形式通过大地传递到邻近建筑物,可能对建筑结构以及建筑物内的振动敏感设备或人等产生不利影响。大地中的振动波类似于空气中的声波,但是固体介质及其边界的特性导致固体中存在着很多种波。在各向同性弹性全空间中,有两种波可以传播,统称为体波,从局部激励点以球形向外移动,第一种是P波,也称为压缩波或纵波;第二种是S波,也称为剪切波或横波。还可能出现第三种波,这种波局限于距离自由表面较近处。这种波被称为R波、瑞利波或表面波。垂向简谐线荷载作用下弹性半空间中的波传播的集合衰减规律见图1。
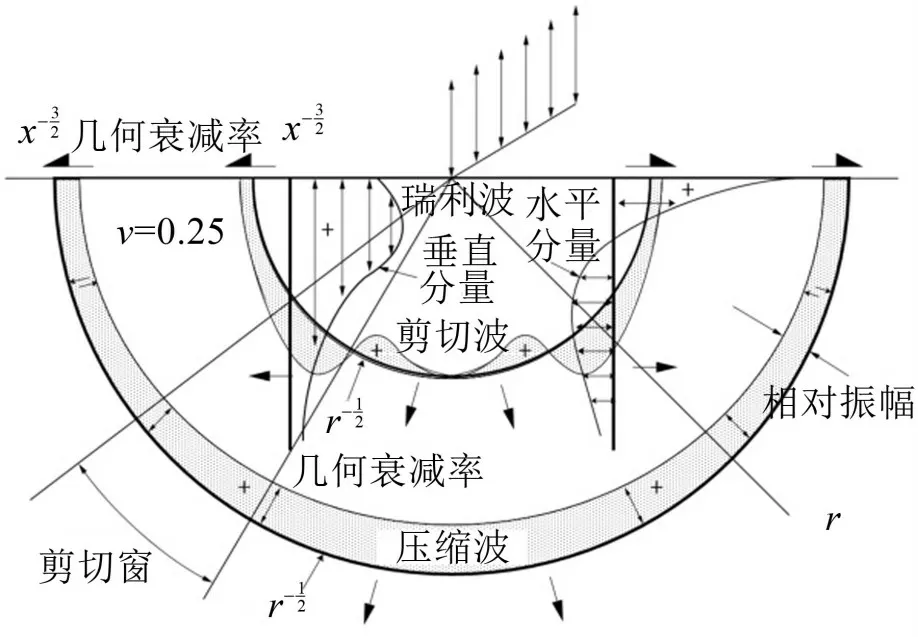
图1 垂向简谐线荷载下弹性半空间中的波传播
振动波在土体中传播时,剪切波波速的计算公式为:
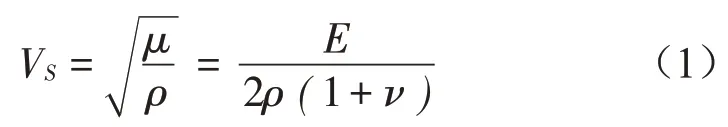
式中:μ为剪切模量;E为弹性模量;ν为泊松比;ρ为密度。
根据目前地面振动传播衰减规律的计算公式结合弹性理论推导、半理论半试验和试验型经验公式,振动波从距离r0传播到r时,地面振动衰减可统一用式(2)表示:
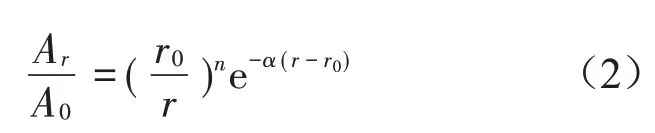
式中:a0和a分别是距离振源r0和r处的振动加速度。
式(2)中第一项表示几何衰减,第二项表示土层的损耗衰减。
1.2 地面振动传递复合回归
地面振动复合回归是把由一元回归所得到的幂函数和指数函数两个函数方程再一次回归拟合,从而得到在所有点上误差均较小的复合函数方程。
(1)将实测所得数据Ar与对应值r,采用幂函数和指数函数曲线进行回归拟合,地面振动衰减规律的计算表达式为:

式中:a1、a2、b1、b2为待定参数。
(2)在图2 中任取距振源ri处的实测振幅Ai对应于幂函数1 曲线和指数函数2 曲线上的振幅值Ai1、Ai2,对应的振幅差mi1=Ai-Ai1、ni2=Ai2-Ai,Ai1、Ai2的取值比例αi1、αi2分别按式(4)、式(5)计算:
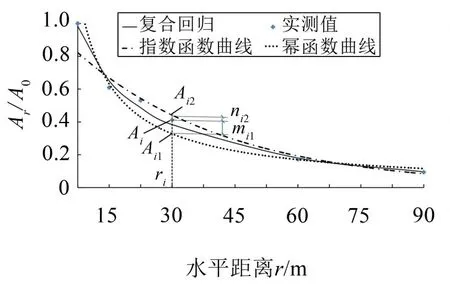
图2 Ar-r说明图
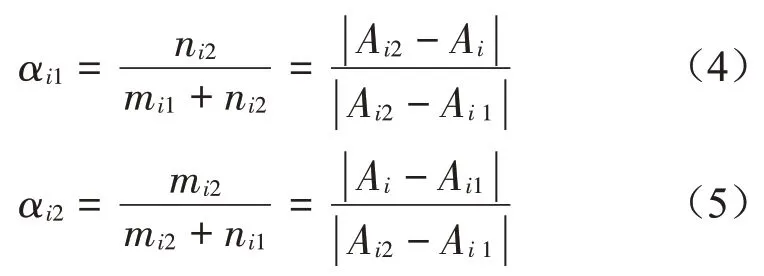
当测点数i=N时,αi1、αi2必须取均值。即:

且有α1+α2=1。将式(2)中以Ar-r表达的幂函数和指数函数进行线性化处理,得:
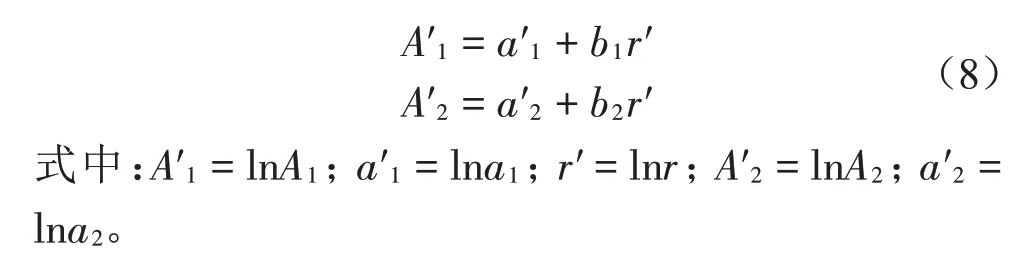
根据线性叠加原理,将线性化方程式(7)分别乘以取值比例ai1、ai2,由此得复合后的线性化方程:

将式(9)代入式(8),可得:
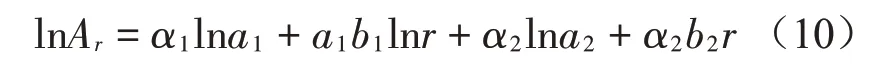
消除对数形式后,则式(9)可写成:
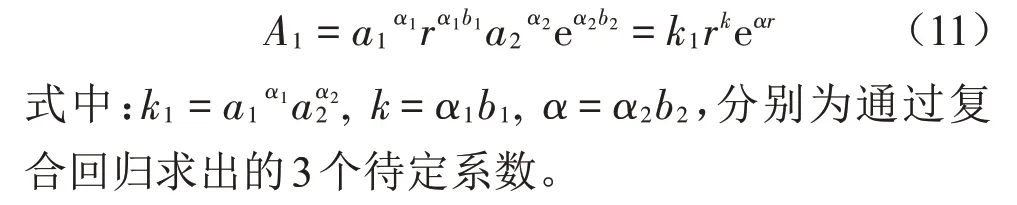
2 实测地面振动传递规律及时频特性分析
2.1 试验概况
某城市地铁地面线路采用地铁列车B 型车,试验现场为平原地貌,地质土类型以粉质填土、杂填土、粉土、粉质黏土、粉细沙和中细沙为主。测点垂直于线路方向,位于距离线路中心7.5 m、15 m、22.5 m、30 m、60 m 和90 m 处。采用高精度压电式铅垂向加速度传感器,量程为0.12 g,灵敏度为40 000 mV/g,采样频率为1 024 Hz。采用INV306 型24 位的智能化高精度数据采集系统作为数据采集设备,其可根据预设程序自动触发、采集、存储。试验地点及周边环境见图3,测点布置见图4。
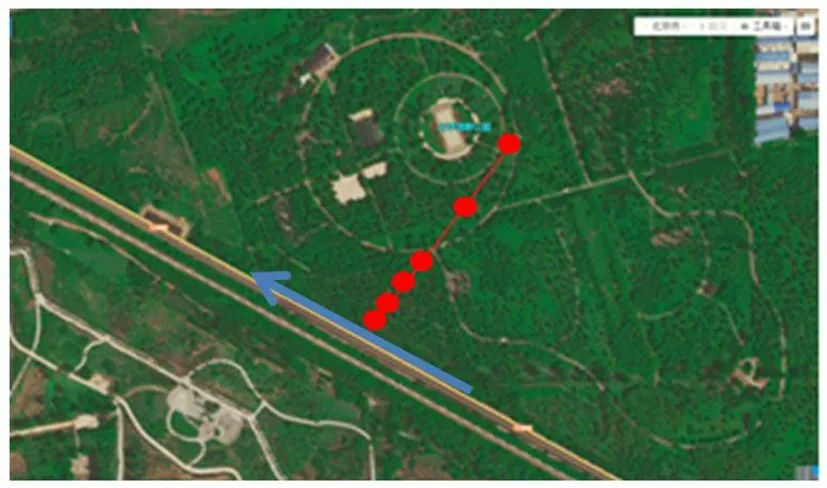
图3 试验地点、周边环境及测点

图4 测点布置示意图
城市轨道交通列车引起的地面振动是一种复杂的随机振动,振动波对地面建筑物和人体舒适度的影响实际上是由振动能量的传递造成的,文中运用傅里叶变换和1/3 倍频程分析不同频段的振动能量分布。
振动加速度级VAL为:

其中:a为列车通过时的振动加速度有效值,m/s2;a0为基准加速度,a0=10-6m/s2。
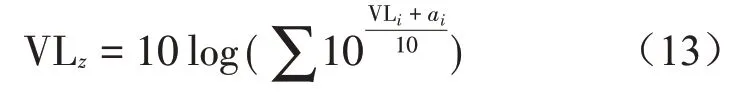
其中:VLz为Z振级,单位为dB,VLi为1 Hz~80 Hz范围内1/3 倍频程第i个频带的振动加速度级,单位dB;ai为第i个频带的计权因子,单位为dB。
2.2 地面振动时频特性分析
通过现场测试得到列车通过时7.5 m、15 m、22.5 m、30 m、60 m、90 m处铅垂向振动加速度时程、频谱见图5。
(1)从图5中可以看出:地面振动加速度随与线路距离的增大逐渐衰减,振动加速度呈宽频特征,频率为20 Hz~100 Hz 的成分数值较大;随距离的增加,高频成分幅值衰减明显。
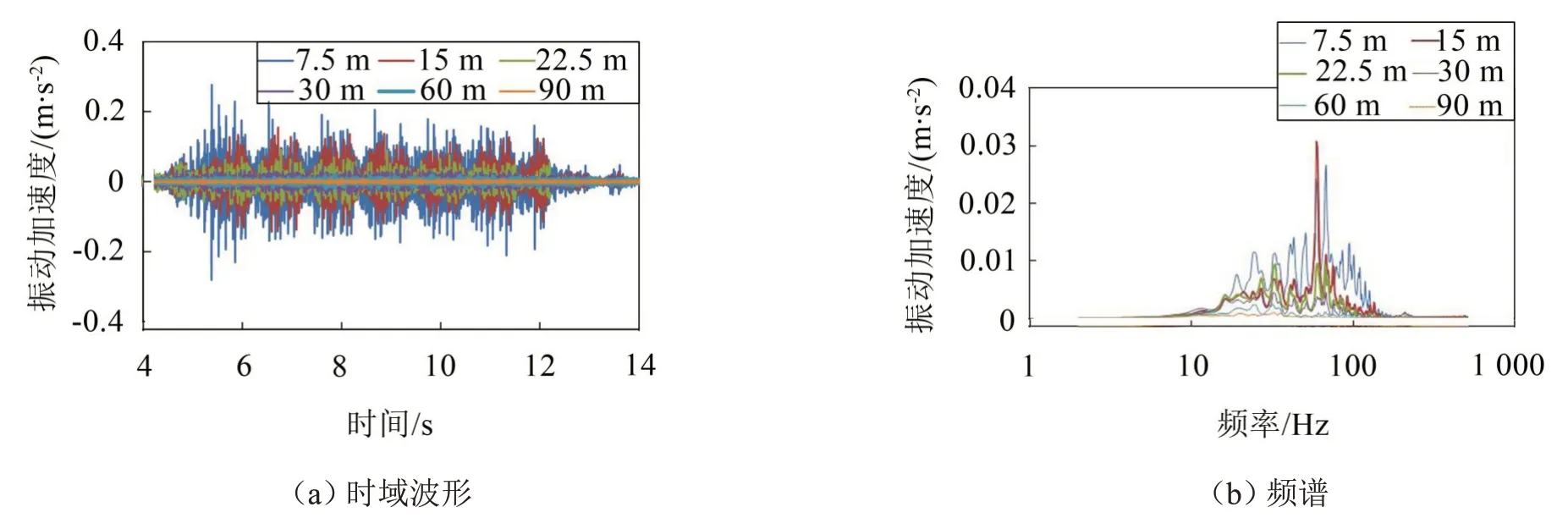
图5 地铁列车通过时不同距离处的地面振动加速度
(2)实际大地比均匀半空间复杂得多,大地是分层的,层与层之间、土体与土体之间材料组成和属性各不相同,在横向和垂直方向不均匀,并且通常各向异性。在这种条件下,表面波表现为弥散波并呈现出多种波类型。弥散波传播速度具有频率和波长依赖性。因此,不同频率的振动在实际大地中传播和衰减特性可能是大不相同的。列车平均速度为60 km/h 时,地铁引起距离线路7.5 m 近场处的振动信号的有效持续时间平均为7 s,随着与线路的水平距离的不断增大,振动持续时间增长,60 m 处的振动信号持续时长达到30 s 以上,且低频成分的振动持续时间明显长于高频振动。
(3)地面振动具有一定的周期性激励频率,地面振动加速度在28 Hz~32 Hz、40 Hz~60 Hz 出现峰值。28 Hz~32 Hz对应于轨枕间距激励引起的频率,40 Hz~60 Hz 为轮轨耦合作用对应的频率。其中轨枕间距(或扣件间距)激励频率fz(Hz)为:

式中:v为列车速度,单位为km/h;lz为轨枕间距,单位为m。
(4)振动波从距离r0传播到r时,土层材料损耗对振动波衰减的作用以e-α(r-r0)表示。
α是由于土体吸收振动能量而使振动衰减的特定系数;α与距离衰减因子D的关系能以式(15)表示:
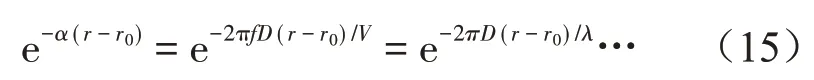
式中:V为波传播速度,单位m/s;f为频率,单位Hz;λ为相应的波长,单位m;D为与损耗有关的距离衰减因子。
式(16)给出了距离衰减因子D与损耗因子η的精确关系。对于低损耗因子,D近似为D=η/2,只要η低于0.3,该式近似成立。差值r-r0是振动波的实际传播距离。从式(15)可以看出,振动波在传递过程中每个波长距离的损耗衰减率为常数。式(17)中α为土体对振动能量的吸收系数。
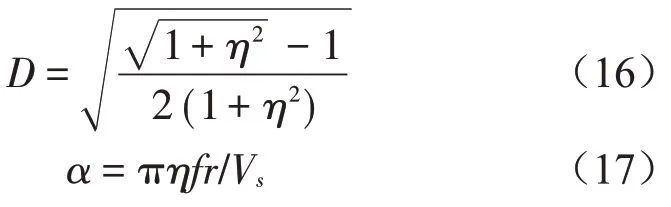

图6 地铁列车通过时不同频率下的地面振动衰减曲线

图7 不同频率下的土体吸收系数
为了得到不同频率成分的地面振动衰减特性,以r0等于7.5 m处地面作为基准参考点,对不同频率下不同距离处地面振动进行复合回归分析,结果见图8。由此可计算得出,土体吸收系数α与频率基本呈正比,即频率越高,衰减越快,土体吸收系数与频率基本成正比关系,比例系数为3×10-4;即5 Hz的振动衰减系数为0.001 5 m/s2/m,50 Hz 振动衰减系数为0.015 5 m/s2/m。
(5)地面线Z振级地面振动衰减
同理,对于地面环境振动,D的相关参数可通过幂函数和指数函数复合回归的方法得到。根据式(11)可知,D的计算公式可简化为:

式中:k3为与振源和土类有关的振幅系数;k为综合衰减系数;r为距离线路中心线的距离,m;α为土对地面振动能量的吸收系数。
对式(18)取对数得:
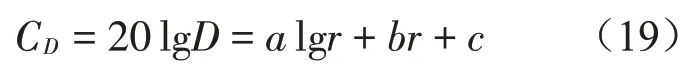
即:a=20k,b=20×0.434 3a=8.686a,c=20 lgk3。
图8至图10为不同距离处地面VLZmax振动衰减曲线,最后得到中软土条件下地面线所致地面振动VLZmax水平距离的修正公式为:
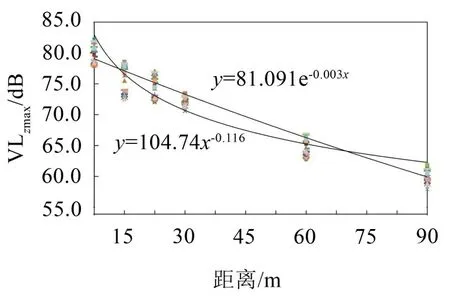
图8 不同距离地面VLZmax
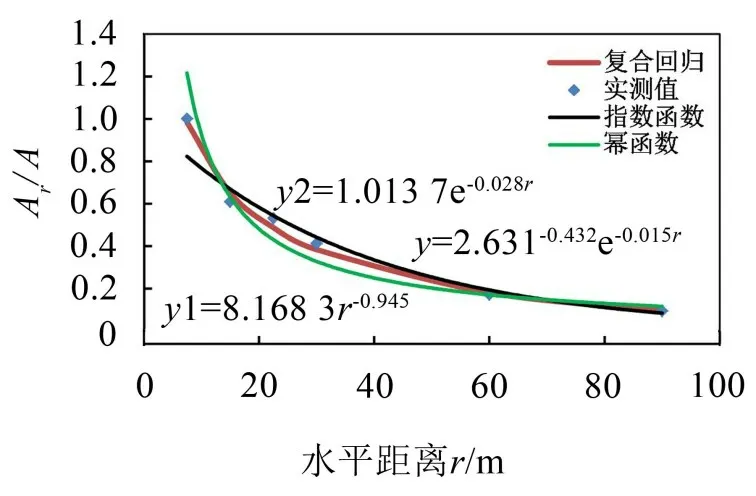
图9 不同距离地面AM复合回归

图10 不同距离地面VLZmax的修正值

3 结语
针对城市轨道交通地面线,基于分析振动衰减的复合回归方法,以距线路中心100 m 范围内自由开阔场地为研究区域,分别将距线路中心7.5 m、15 m、22.5 m、30 m、60 m、90 m处实测的地面振动数据进行对比分析,从时域与频域的角度分析地面线路所致振动波传播机理,其结论为:
(1)地面线所致振动传播以表面波为主,随与线路的距离的增大逐渐衰减;振动加速度呈现宽频特征,频率为20 Hz~100 Hz 的成分数值较大;高频振动幅值随距离的增加衰减明显。
(2)地面振动具有一定的周期性激励频率,对应于轨枕间距激励引起的频率和轮轨耦合作用的频率。土体吸收系数α与频率基本呈正比,即频率越高,衰减越快,比例系数为3×10-4。
(3)采用复合回归方法导出了中软土条件下地面线所致不同距离处地面振动VLZamx随距离的振动衰减曲线为:
VLZmax(r)=VLZ0max-8.6 lgr-0.13r+8.4,其中VLZ0max为7.5 m处的振动源强,单位为dB。
