改进VMD-LSTM的轧机振动预测研究

张瑞成，曹志新，梁卫征

（华北理工大学 电气工程学院，河北 唐山 063210）

轧机振动问题由来已久，剧烈的轧机振动不仅会造成板带材薄厚不均，产生明暗条纹，严重时还会威胁设备和人员安全[1]。以往专家学者对轧机振动的研究主要集中在建立轧机振动机理模型[2－3]、振动信号分析[4]以及振动抑制方面[5]，由于实际轧制系统具有多变量、非线性等特点，建立精确数学模型难度较大，传统信号处理方法具有局限性。随着人工智能技术的不断完善和发展，人工神经网络凭借其高度非线性、大量数据并行处理、高鲁棒性等优势在钢铁轧制领域得到了广泛应用。

Wang等[6]提出了一种基于遗传算法优化人工神经网络的弯曲力预测方法，相关性系数达0.983。Wu 等[7]提出了一种基于混合模拟退火算法和遗传算法优化极限学习机的弯辊力预测方法。马威等[8]采用深度前馈神经网络实现了对轧制力的准确预测。Lu 等[9]分别采用支持向量回归、反向传播神经网络（Backpropagation，BP）和极限学习机实现了对轧机振动的监测和预警，并分析了各工艺参数对轧机振动的贡献率。董志奎等[10]采用深度置信网络（Deep Belief Networks，DBN）对轧制过程数据进行深度特征提取，建立了基于DBN-BP 轧机垂振预测模型。

目前，在应用人工神经网络预测轧制力方面已取得了大量成果，但在轧机振动方面研究较少，且以往对于轧机振动多采用传统神经网络预测方法，忽略了轧机历史输入输出对轧机振动的影响。为此，提出了一种基于改进VMD-LSTM 的轧机振动预测方法。

1 改进VMD-LSTM 轧机振动预测模型

1.1 改进VMD分解

VMD作为一种完全非递归、自适应的信号处理方法，适合用于处理非线性、非平稳特性的数据，克服了经验模态分解（Empirical Mode Decomposition，EMD）所存在端点效应和模态混叠问题，其核心是构建和求解变分问题。VMD分解的一般过程[11]为：

(1)构造变分问题；

(2)引入拉格朗日乘法算子和二次惩罚因子，将约束变分问题转换为非约束变分问题；

(3)采用交替方向乘子进行更新迭代得到各模态分量（Intrinsic Mode Function，IMF）及其对应的中心频率。

由于进行VMD 分解需要预先设定参数K，K值的设定对VMD分解结果有较大影响。为此，将巴氏距离[12－13]引入到VMD 中，计算经VMD 分解得到的两两模态分量间的最小巴氏距离并与最小巴氏距离阈值a比较，当DBmin小于a时，VMD 分解结果为最优分解结果，如图1所示。

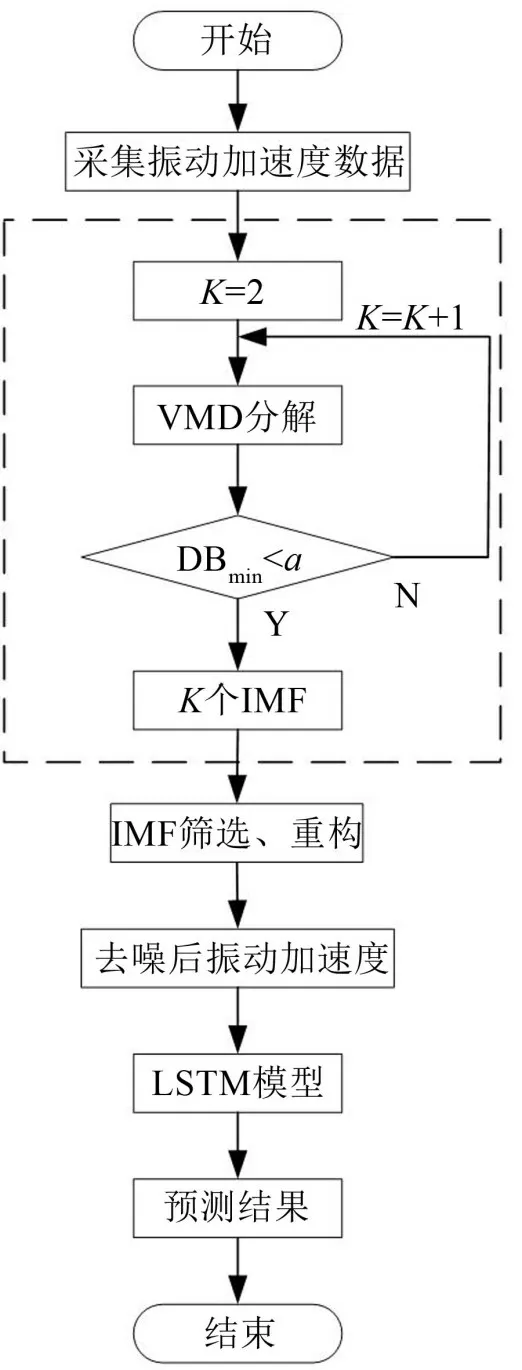
图1 改进VMD-LSTM预测流程图

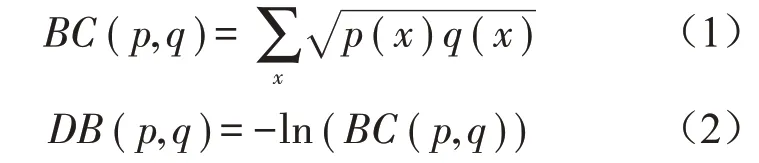
式中：p、q为两个分量的离散概率分布，BC为巴氏系数，DB为巴氏距离。

1.2 LSTM网络

LSTM 网络[14]是一种特殊的循环神经网络，它克服了其难以训练和梯度消失问题。通过引入门限结构实现对历史信息的记忆和更新，如图2所示。

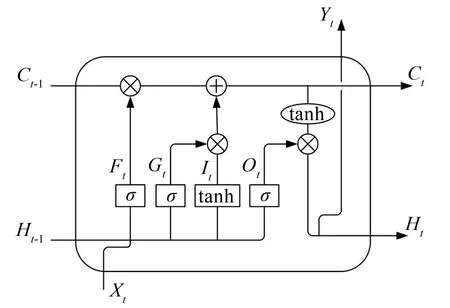
图2 LSTM单元结构图

LSTM 网络主要由遗忘门ft、输入门it和输出门ot组成，其中，ft控制历史信息的保留，it决定需要存储的信息，ot控制LSTM单元细胞状态过滤情况，如式（3）至式（8）所示：

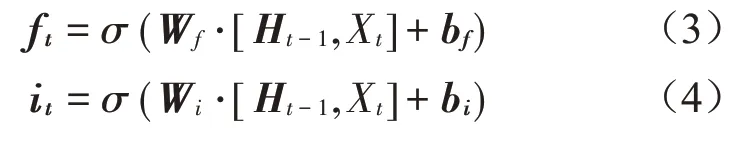
式中：Wf、Wi、Wc、Wo为相应的权重矩阵；bf、bi、bc、bo为相应的偏置矩阵；Xt、Yt代表单元的输入和输出；Ht-1、Ct-1代表上一单元的输出和信息状态；Ht、Ct代表本单元的输出和信息状态；代表输入门的候选信息状态；σ为sigmoid函数。

1.3 基于改进VMD-LSTM轧机振动预测模型

针对冷连轧机振动问题，基于巴氏距离最小对VMD 的关键参数K进行优化选取，建立基于VMDLSTM的轧机振动预测模型。

具体步骤如下：

（1）数据采集：采集轧制过程数据和上工作辊振动加速度数据；

（2）改进VMD 分解：设置VMD 初始K值为2，二次惩罚因子为α，最小巴氏距离阈值为a，将现场采集的振动信号进行VMD分解。

（3）选取重构主要模态：根据相关系数Q2和能量占比P选取主要模态分量，并对主要模态分量进行叠加重构；

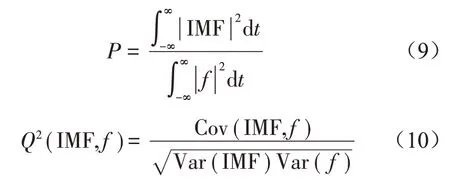
式中：Cov为协方差，Var为方差，f为原始振动信号。

（4）建立LSTM 预测模型：将入口张力、硬度等作为输入，重构信号作为输出，建立基于LSTM振动预测模型。利用训练集进行训练，测试集进行验证。

（5）性能评估：采用平均绝对误差（Mean Absolute Deviation，MAE）、均方根误差（Root Mean Squard Error，RMSE）以及决定系数（R-squared，R2）评价预测模型性能。

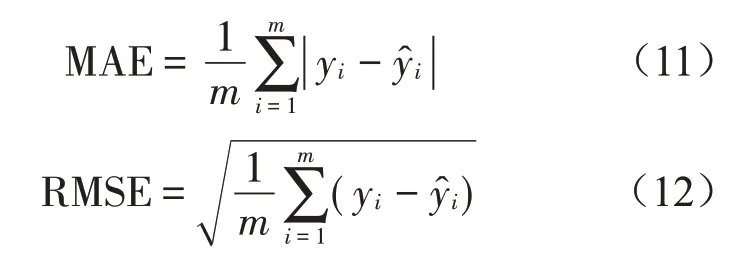
式中：m为测试集样本数，yi为振动加速度实测值，为模型预测值，为振动加速度实测值的平均值。

2 仿真分析

针对某厂轧机在轧制高强薄板时易产生垂振问题，对该机架进行了振动综合测试，得到如表1所示的1550组振动实测数据。由于轧制环境恶劣，轧机振动信号普遍存在干扰，为提高LSTM 网络预测精度，对现场采集的轧机振动加速度信号进行去噪处理。

表1 轧机振动实测数据

初始化VMD分解（K=2），根据经验设置二次惩罚因子α为2 000，阈值a为0.001，对现场采集的振动加速度进行VMD分解。当K为4时，DBmin小于阈值0.001，VMD分解结果如图3所示。

图3 改进VMD分解

根据相关系数和能量占比选取主要模态分量。计算各模态分量与原始信号的相关系数，如表2 所示。根据经验取相关系数阈值低于0.1 的分量作为噪声分量[15]。

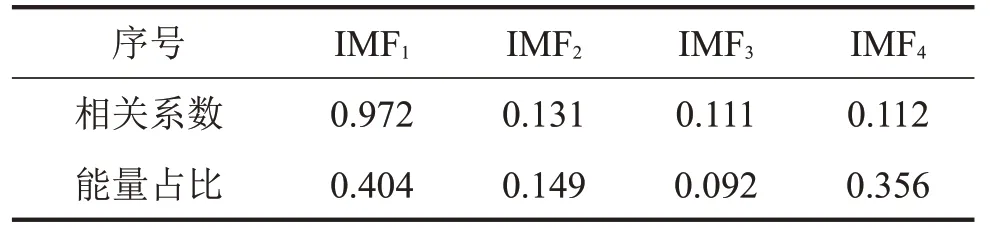
表2 IMF性能指标

由表2 知IMF3、IMF4相关系数分别为0.111 和0.112，与阈值0.1 较为接近。为进一步确定噪声模态分量，对IMF1～IMF4进行能量占比计算，可知IMF3能量占比最小仅为0.092，综合考虑相关系数和能量占比，选取IMF1、IMF2、IMF4为主要模态分量，并对其进行叠加重构得到重构信号。

设置LSTM 网络输入维度为5，输出维度为1，选取单层网络，隐含层神经元为200，训练次数为300，初始学习率为0.005，第125 次训练后降低为初始学习率的0.2倍，采用自适应矩估计对LSTM网络进行调优，将入口厚度、入口张力、出口张力、出口厚度、硬度作为输入，重构信号作为输出，建立基于LSTM的轧机振动预测模型。

利用重构的前1 250 组数据构成训练集对LSTM网络进行训练，将后300组构成测试集用于检验，得到如图4所示的轧机振动预测结果。其中，虚线为重构后的振动加速度，实线为VMD-LSTM模型的预测结果。由图4可知，基于改进VMD-LSTM的轧机振动预测模型能够实现对轧机振动的准确预测。

图4 改进VMD-LSTM预测模型

为检验改进VMD-LSTM 轧机振动预测模型性能，将其分别与BP 模型、LSTM 模型和EMD-LSTM模型进行对比。由表3 可知，LSTM 模型优于传统BP 模型；组合预测模型优于单一模型；改进VMDLSTM模型优于其他3种模型。

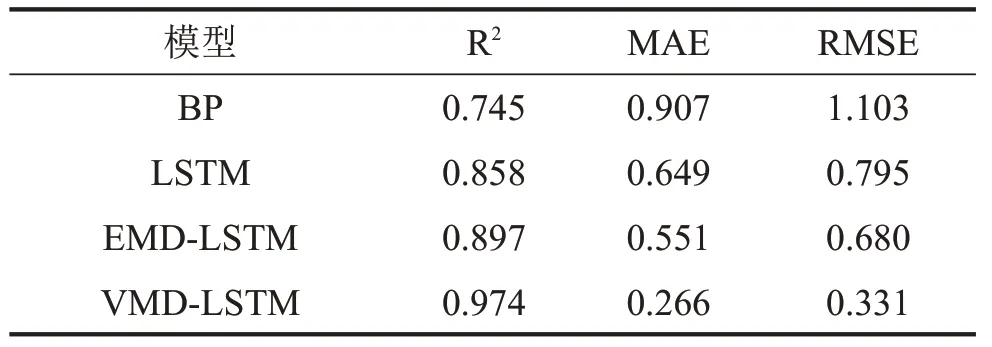
表3 预测性能对比

3 工艺参数改变对轧机振动影响

为分析各工艺参数改变对轧机振动的影响，随机选取了一组振动加速度为0.161 g的样本数据，如表4 所示。通过单一改变（增加或减小5%）某一输入参数，构造了7 组测试数据，依次将7 组数据输入到基于改进VMD-LSTM的轧机振动预测模型中，如图5所示。

表4 轧制工艺参数

图5 各工艺参数改变对加速度影响

以入口张力改变为例，当改变量为0时，其预测值接近实测值0.161 g，说明预测模型性能较好。当入口张力减小时，振动加速度减小，入口张力增大时，振动加速度增大。以同样方式对出口张力、入口厚度、出口厚度、硬度逐一分析。由图5 可知：入口张力、出口张力、入口厚度改变对振动影响较大，出口厚度改变对轧机振动影响次之，硬度改变对振动几乎没有影响。

4 结语

针对冷连轧机由于具有非线性、强耦合等特性而导致轧机振动预测难度较大问题，提出一种基于改进VMD-LSTM轧机振动预测方法。仿真表明：采用最小巴氏距离改进VMD 分解对轧机振动加速度进行去噪处理，可有效提高轧机振动预测精度；通过与BP 模型、LSTM 模型和EMD-LSTM 模型进行对比分析可知，基于VMD-LSTM的轧机振动预测模型预测精度最高；分析了各工艺参数改变对轧机振动的影响，可为快速抑制振动提供参考。在生产过程中，通过对VMD-LSTM振动预测模型进行离线训练和模型在线运行，能够实现对轧机振动状态实时预测，指导生产实际。