EEMD-四线性平行因子的机械多故障欠定盲分离方法
2022-12-20朱亚静李泽东李志农谷士鹏马亚平
朱亚静,李泽东,李志农 ,谷士鹏,马亚平
(1.南昌航空大学 无损检测教育部重点实验室,南昌 330063;2.中国飞行试验研究院,西安 710089)
平行因子(Parallel Factor,PARAFAC)在宽松条件下具有分解唯一性的优势,在机械故障诊断中获得了成功应用。李晓明等[1]将传统奇异谱分解结合标准PARAFAC 张量分解方法进行扩展,对机械故障特征进行提取。苗育茁等[2]利用连续小波变换构造3 阶张量,通过PARAFAC 对其进行分解,提出了一种多尺度平行因子分析算法,可以有效地从机械非线性多故障状态中提取特征,进行故障诊断。杨诚等[3]结合Volterra 模型与PARAFAC 构建了故障预测模型,主要解决了PARAFAC 在分解机械非线性系统信号时估计参数较多的问题。李志农等[4]结合变分模态分解(Variational Mode Decomposition,VMD)和PARAFAC 各自优点,提出了基于VMDPARAFAC欠定盲分离方法,并将其应用到滚动轴承的复合故障特征提取中。孙宜权等[5]采用自适应PARAFAC 和BSS 算法对柴油机喷油多故障进行诊断。然而,上述方法中的PARAFAC 分解都是通过构造3阶张量完成的,采用三线性PARAFAC进行机械故障诊断时,只能对振动信号的部分信号建模,存在信息不完整的问题。在平行因子的发展过程中,四线性PARAFAC 的提出具有重要的意义。四线性PARAFAC具有三线性平行因子所不具有的优势,且采用四线性平行因子盲分离算法可有效地对机械多故障进行源数估计,更好地分解信号,提取故障特征[6]。然而,在研究机械多故障欠定盲分离时,通常情况下对四线性PARAFAC 模型采用QALS 迭代拟合,而在欠定条件下,收敛过程中会出现陷入局部收敛的问题,得到的估计源信号往往不是很理想。
集成经验模态分解(Ensemble Empirical Mode Decomposition,EEMD)是针对经验模态分解的不足而提出的1 种噪声辅助数据分析方法,该方法充分利用白噪声均值为零的特点,使得由于干扰导致的任何尺度的信号所出现间断,都能得到白噪声的补充,使间断信号在相应尺度形成连续信号,该方法很好抑制了由于 EMD(Empirical Mode Decomposition,EMD)分离所导致各分量之间出现混频现象[7]。文献[8]结合EEMD和具有自适应增长特性的输出隐藏反馈Elman网络对滚动轴承进行诊断。文献[9]将EEMD 应用于机械故障中的复杂信号处理,提取故障特征。文献[10]提出1 种改进的EEMD 方法,以消除在EEMD 方法中只添加噪声而导致的局限性,结果表明所提方法可以抑制机械信号模态混淆并且在故障诊断方面效果明显。文献[11]将EEMD 和散布熵结合,构建故障信号的高维特征,在结合LPP-KNN 进行故障诊断。文献[12]将集合经验模态分解(EEMD)和低相干K-SVD相结合进行齿轮故障特征提取。上述研究均表明EEMD在进行机械振动信号分解时具有独特的优势。
在此,结合四线性平行因子盲分离算法和集合经验模态分解算法(EEMD)的的独特优势,提出了一种基于EEMD分解的四线性PARAFAC欠定盲源分离方法。该方法首先利用EEMD分解传感器所采集的观测信号,接着从分解得到的IMF 分量中选出恰当相关IMF分量信号。根据选出的相关IMF分量与原观测信号重新构造信号,使得经四线性分解处理的重组信号数大于或等于源信号数,这样盲分离中的欠定就被转换为正定或超定。最后利用四线性交替最小二乘法迭代(Quadrilinear Alternating Least Squares,QALS)进行拟合迭代,得到混合矩阵估计,用最短路径法得到源信号估计。然后,通过仿真和实验研究以验证该方法的有效性。
1 EEMD-四线性平行因子盲分离方法
信号线性混叠模式可以表示为如下形式:
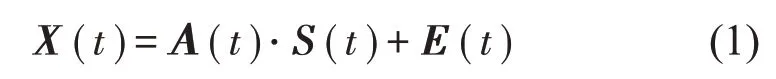
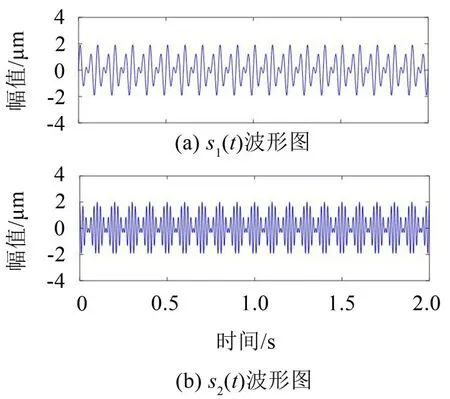
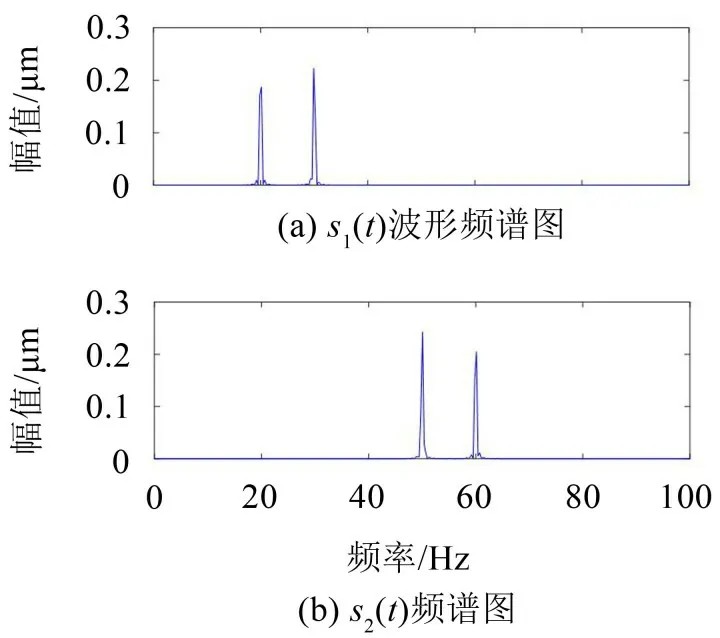
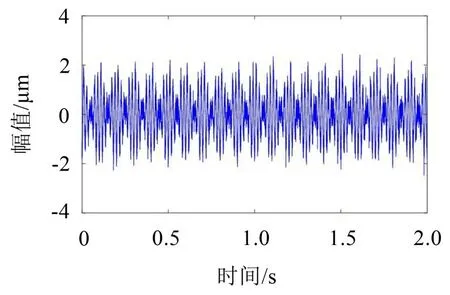
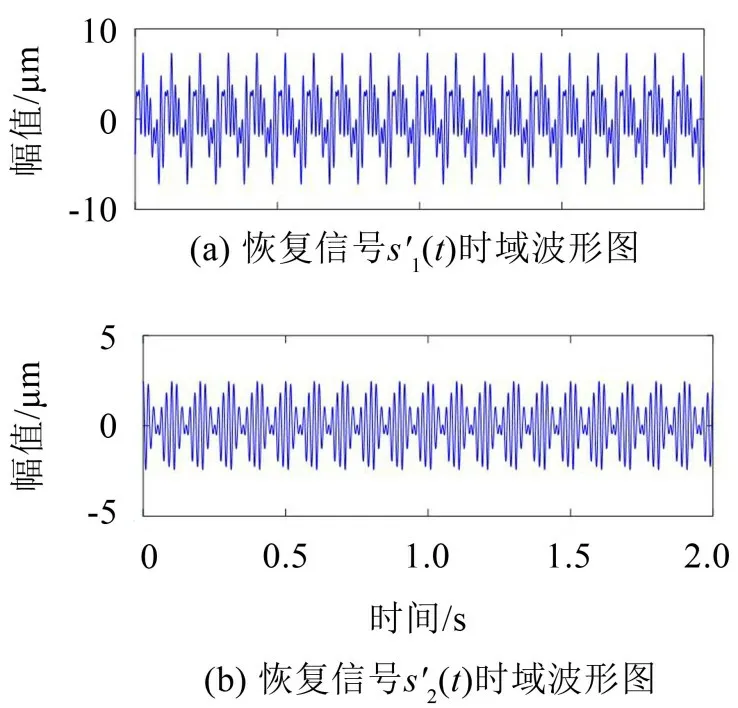
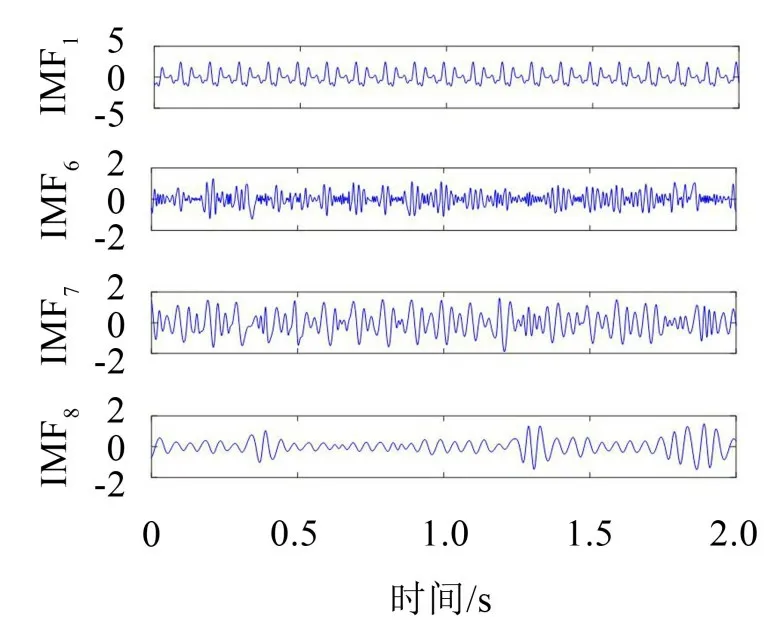
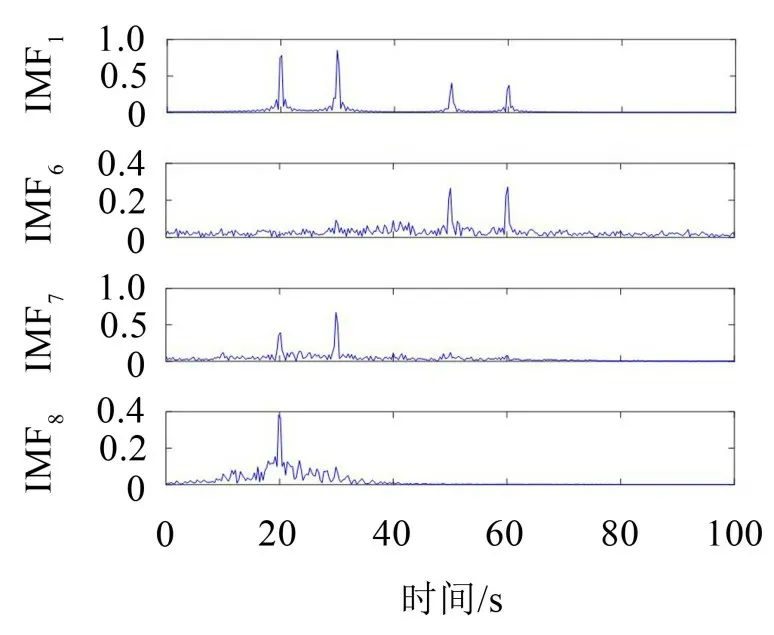
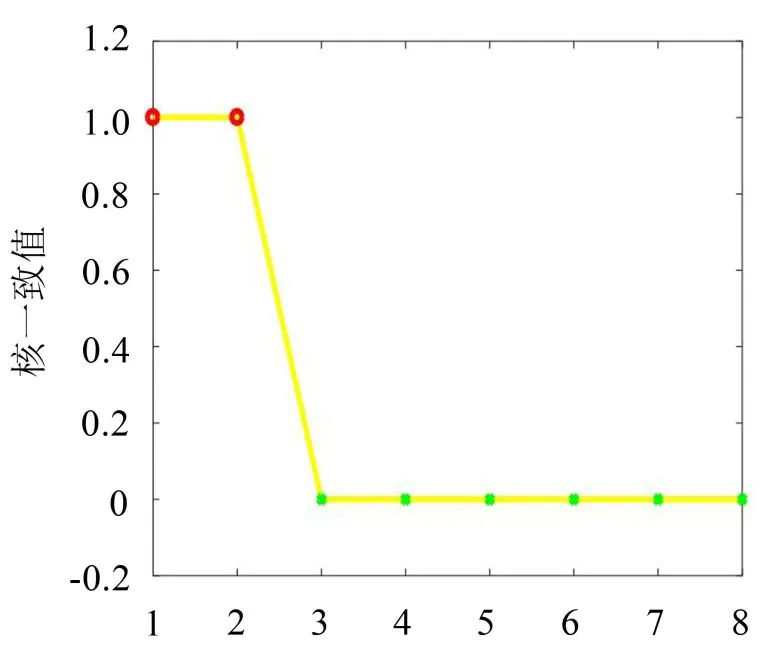
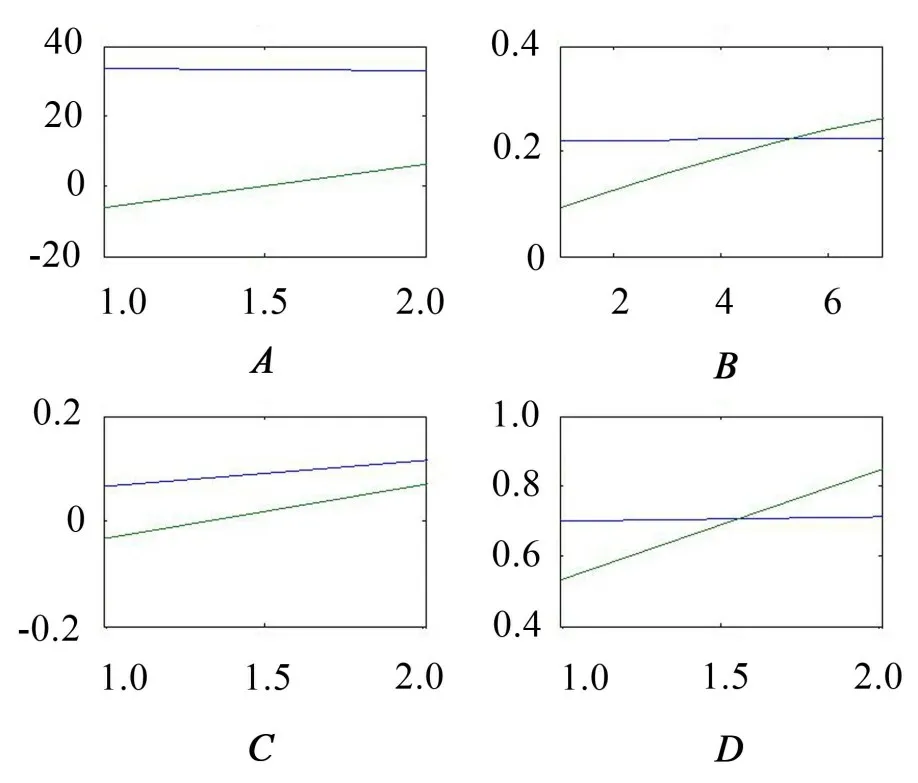
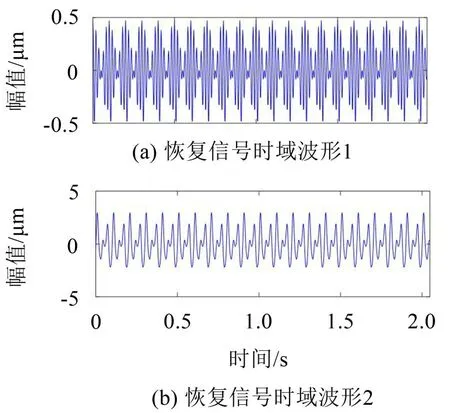
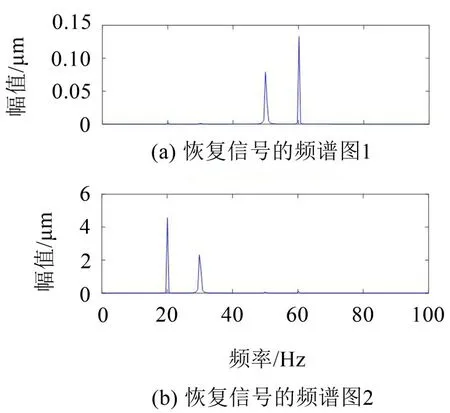
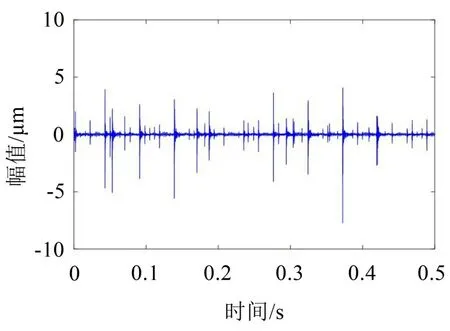
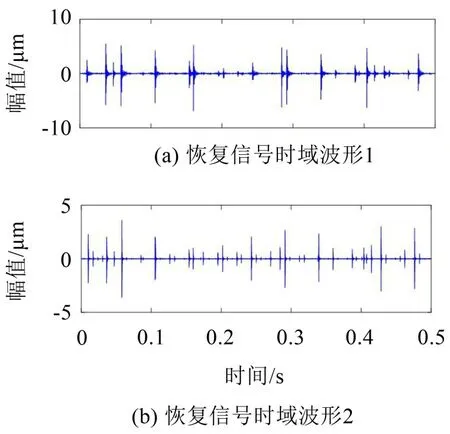
式中:S(t)=[s1(t),…,sM(t)]T为源信号矩阵,每个源信号包含L个数据点,A(t)是N×M维的混合矩阵(N 在观测信号X(t)中加入白噪声信号,利用EEMD方法将含噪的观测信号分解成多个IMF信号分量。具体步骤如下: 第一步:首先在处理观测信号X(t)=[x1(t),…,xN(t)]T前设定平均处理次数M,其中i=1,2…,M; 第二步:接着在观测信号X(t)添加白噪声ni(t),将加入白噪声的信号作为一个整体,然后与原观测信号组成新的观测信号Xi(t)=X(t)+ni(t); 第三步:用EMD分解Xi(t)得到IMF,得到子分量ci,n(t); 其中:ri,n(t)是得到的残余分量; 第四步:重复前面3个步骤,通过分解得到新的一系列的IMF; 第五步:对得到的IMF 分量进行M次平均获得cn(t); 其中:i=1,2…,M;n=1,2…M。 第六步:利用相似系数公式求通过分解得到的IMF 分量相关系数,然后选取相关性较大的有效IMF。 选取相关性较强的IMF 信号分量,并将其与原来的传感器数据组合,构建新的观测信号X(t)。这样,实现了将欠定条件下的盲源分离转化为正定或超定条件下盲源分离。然后将经中心化处理后的观测信号进行分段处理,其被均匀划分成J个不会重叠的数据段,经计算可知每段的数据点数为L/J个,记其为K,即K=L/J,具体段数可以任意选择,若最后一段的点数不够,可以补零。每一个数据段对应的采集时间为h,则其共被分为t/h个时间段,记其为I,此时: 信号块的时滞协方差矩阵为: 其中:k=1,2,…,K,序号tk表示t内第k个数据点。 传感器在h段采集到的各源信号数据时滞协方差Rn可以通过计算得到,有: 式(6)中:tk表示t内第k个源信号。将块时滞协方差矩阵转换成为对角阵,并且使该矩阵等于矩阵B,将源时滞协方差矩阵转换成为对角矩阵并且使该矩阵等于矩阵C,则式(5)、式(6)可以分别改写为式(7)和式(8)。 将源时滞协方差矩阵以及块时滞协方差矩阵叠加,叠加后所得的3阶矩阵计为RJ,K 其中:n=1,2,…,N,k=1,2,…,K。 相邻对角阵相乘可以换位,则式(9)可表示为: 将式中N×K个切片累积成N×J×K×I维的R(四维数据集)。 其 中:n=1,2,…,N,k=1,2…,K,j=1,2,…,J,i=1,2,…I,式(11)即为所构造的EEMD-四线性盲分离模型。 如上实现了集合经验模态四线性平行因子盲源分离算法的构建,其分解过程中采用QALS 得到混合矩阵估计A′。分解算法的主要思想为让上一次估计更新的矩阵参与下一次的矩阵求解,同时使根据最终估计得到的4个载荷矩阵与被分解矩阵的差值尽量最小,迭代过程步骤分为4步。 第二步:将A重新代入式(12),接着最小化式(12)得到估计的,令其等于B,更新矩阵B。 第三步:将求得的矩阵B重新代入式(12),接着最小化式(12)得到矩阵估计,令其等于C,更新矩阵C。 第四步:将按照以上循环步骤得到的载荷矩阵代入式(17),若满足式(17),则退出,反之继续。 一般认为ε为1×10-6,ςς3是残余误差的平方和,表示含噪的切片,‖∙‖F为Frobenius 范数,i=1,2,…,I,j=1,2,…,J,上标+为Moore-Penrose伪逆,和表示A、B和C的上一次估计,m为迭代次数。 当式(17)所示的停止准则得到满足即表示矩阵更新结束算法收敛,得到最终的混合矩阵估计A′,令A′=A。 令ai为A第i个列向量,si(t)表示源信号的第i个源向量。线性混叠模型X(t)=AS(t)可以表示为: 其中:X(t) 是观测信号,它可以表示成a1s1(t)、a2s2(t)、…、ansn(t)的累加。ai表示矢量方向,si(t)表示向量长度。对于欠定混合的情况,采用最短路径法[9]恢复源信号。推断源的问题可以用式(19)表示: 由式(18)以及式(19)即可得到源信号估计。其主要思想是求每个时刻最优解,然后得到恢复的源信号。 构造的两个仿真信号s1(t)、s2(t)如式(20)所示,式中:f1=20 Hz,f2=30 Hz,f3=50 Hz,f4=60 Hz。 选取采样频率fs=5 000 Hz,采样点数N=20 000。绘制两个源信号s1(t)、s2(t)的时域波形如图1所示。相应的频谱如图2所示。 图1 源信号时域波形图 图2 源信号频谱图 用1×2 维的随机混合矩阵A,将两个源信号s1(t)、s2(t)进行随机混合,混合后得到1 路的混合信号如图3所示。已知源信号的个数为2,混合后观测信号的个数为1,因此,该盲源分离问题为欠定求解问题。 图3 混叠信号时域波形图 利用四线性平行因子盲分离算法将该混合信号分离,得到恢复源信号如图4 所示。相应的频谱如图5所示。 图4 恢复信号时域波形图 图5 恢复信号的频谱 对比图4和图1可知,采用四平行因子盲分离算法得到的恢复信号与源信号相似度不是特别高,分离效果不理想。由图5 可知,分离得到的恢复信号的特征频率分别为20 Hz、30 Hz、50 Hz、60 Hz,与源信号特征频率不一致,分离得到的频谱图效果不是很理想,因此,在欠定条件下直接采用四线性平行因子盲源分离算法分解效果不理想,需对其进一步改进。 为了改进四线性平行因子盲源分离算法的这种不足,用集合经验模态平行因子盲源分离算法分解混合信号。该算法首先用EEMD 算法分解混合信号,通过分离得到14 个子分量,然后选择相关子分量。选择相关分量的具体做法是利用相关系数求各子分量与观测信号的相关度,一般认为信号与观测信号越相似,则相关度的值越接近为1。根据相关度的值定义其在0 到0.3 之间为微相关,0.3 到0.5 之间为实相关,0.5到0.8之间为显著相关,0.8到1之间为高度相关。根据EEMD 算法分解得到的14 个子分量的相关系数如表1所示。 由表1可知,子分量IMF1、IMF6、IMF7、IMF8的相关系数值相对较高,其他分量均为不相关,所以选择IMF1、IMF6、IMF7、IMF8为相关分量并将其与原观测信号组合得到新观测信号,这样就将欠定转化为超定。绘制相关分量IMF1、IMF6、IMF7、IMF8的时域波形图和频谱图,得到的图形分别如图6 以及图7所示。 图6 根据EEMD分解得到相关子分量时域波形图 图7 根据EEMD分解得到相关子分量的幅值谱图 表1 各子分量相关系数 将通过分解得到相关子分量和混叠信号组合,得到新观测信号,用核一致算法估计振源数,如图9所示。 图9 组件数 由图9可知,振源数为2。将得到的观测信号用四线性平行因子盲分离算法处理,用QALS 算法拟合迭代,当达到迭代终止条件时得到4 个载荷矩阵A、B、C、D。由图8 可知,4 个载荷矩阵中,载荷矩阵B、D分解形式相同,表明建立的模型符合式(11)所示的四线性模型,并未偏离四线性模型。 图8 载荷矩阵 用集合经验模态四线性平行因子盲源分离算法处理通过组合得到的观测信号,依据模型求得混合矩阵估计,以及根据式(19)求得估计源信号,绘制恢复信号的时域波形图如10 图所示。相应的恢复信号频谱如图11所示。 由图11 可知,图11(a)中的特征频率分别为50 Hz、60 Hz,图11(b)中的特征频率分别为20 Hz、30 Hz,除排列顺序有所不同外,其分别与两源信号的特征频率相一致,这种排列顺序改变并不影响分离结果的正确性。对比图10与源信号时域波形,恢复信号的时域波形图和源信号时域波形图非常相似。由此可知,提出的方法能够有效分离混合信号,分离效果非常令人满意。对比提出的方法和传统的四线性平行因子盲源分离算法,发现欠定条件下采用四线性平行因子盲源分离算法并不能得到很好的分离效果,而采用集合经验模态四线性平行因子盲源分离算法可以很好分离混合信号并且分离效果比四线性平行因子盲源分离算法好很多,证明了该算法的有效性。 图10 恢复信号时域波形 图11 恢复信号的频谱图 为了验证所提算法的有效性,将集合经验模态四线性平行因子盲分离算法应用于滚动轴承复合故障盲源分离中。实验所需要的数据由滚动轴承诊断试验台采集,试验台由旋转电机、滚子轴承和加速度传感器组成。轴承的代号是N205EM。电机转速约为1 300 r/min,转动频率约为21.7 Hz,采样频率fs=100 kHz。数据中包含一组内滚道和滚子的复合故障信号。使用线切割机技术人为制造缺陷以产生故障源,内圈故障大小为0.3 mm×0.15 mm,滚子故障大小为0.3 mm×0.15 mm,利用轴承故障频率机理公式可计算得到滚子的故障特征频率fb=102.3 Hz,内圈故障特征频率fi=145.7 Hz。所用信号的采样点数为1 001 000,绘制采集的混合观测信号时域波形图,如图12所示。 图12 观测信号时域波形图 将观测信号用EEMD 算法分解,得到16 个IMF分量。利用相关系数法选择相关性较大的子分量,各子分量的相关系数如表2所示。 由表2 可知,子分量IMF1、IMF2、IMF3、IMF4、IMF5的相关系数均大于0.3,为有效子分量,其他子分量信号的相似系数值均在0.3 以下,所以选择IMF1、IMF2、IMF3、IMF4、IMF5为相关分量。将选择的相关子分量与原观测信号组合得到新的观测信号。绘制IMF1、IMF2、IMF3、IMF4、MF5的时域图,得到的图形如图13所示。 表2 各子分量相关系数 图13 采用EEMD分解观测信号得到的有效子分量时域波形图 将分解得到的这5个相关的子分量信号和混叠信号重新构造成新的观测信号,计算观测信号段的时滞协方差矩阵,并将所有数据段的时滞协方差叠加成4阶张量形式,得到四线性模型,用QALS拟合,当满足式(17)时迭代结束,求得估计矩阵。利用所求的估计矩阵和最短路径法得到恢复信号,绘制恢复信号的时域图和频谱如图13、图14所示。 图14 恢复信号时域波形图 由图14可知,采用集合经验模态四线性平行因子盲源分离算法可以有效分离出滚动轴承内圈故障和滚动体故障。分离得到的幅值谱如图15 所示。图15(a)中特征频率有145 Hz以及相应的调制频率,对比计算得到的故障特征频率,发现其与轴承内圈故障特征频率145.7 Hz 基本一致。图15(b)中的特征频率有102.2 Hz 以及相应的调制频率,对比计算所得的故障特征频率,发现其与计算所得的轴承的滚子故障特征频率102.3 Hz基本一致。 图15 恢复信号频谱图 由此可知,运用集合经验模态四线性平行因子盲源分离算法可以有效分离出滚动轴承复合故障,取得了非常满意的分离效果,实验证明了该方法的有效性。 四线性平行因子是三维平行因子的拓展模型,通过其可以获得更多的信息,并在宽松的约束条件下其模型分解也具有唯一性。通过集合经验模态分解可以对时间序列进行局部平稳化处理,适用于任何信号分解,可以解决盲源分离中的欠定问题,基于此,将四线性平行因子和经验模态分解相结合,提出一种基于集合经验模态和四线性平行因子欠定盲分离算法,所提算法利用EEMD重构观测信号,将欠定转换为超定和正定,再使用四线性平行因子对观测信号进行处理,得到源信号的估计。仿真结果表明,采用提出的方法不仅能准确估计出源信号数目,而且还能估计出源信号。最后,将提出的方法应用到滚动轴承复合故障诊断中,实验结果进一步验证了提出的方法的有效性,内圈故障和滚子故障的特征频率及相应的调制频率都得到了充分的反映。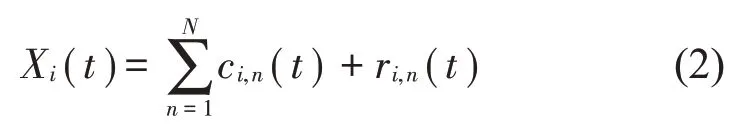

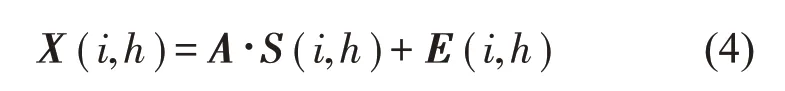
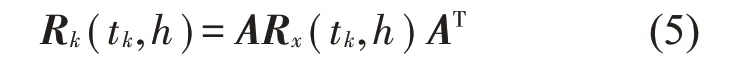
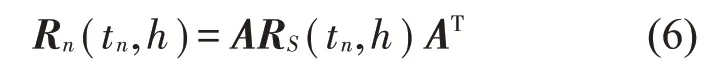


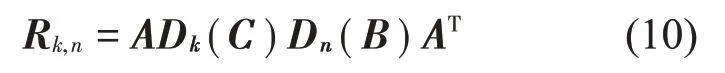
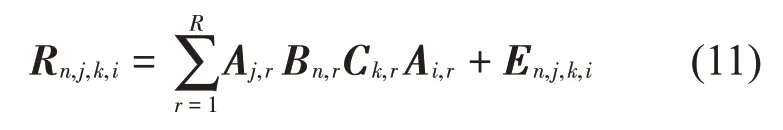

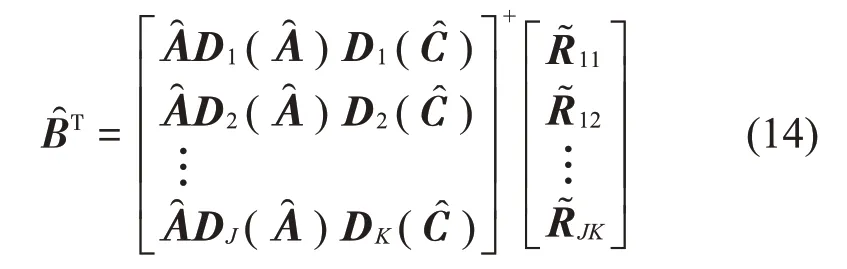



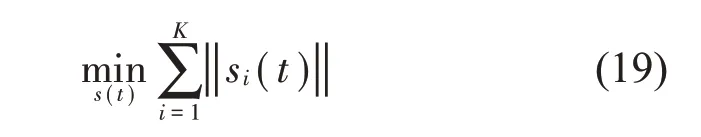
2 仿真研究
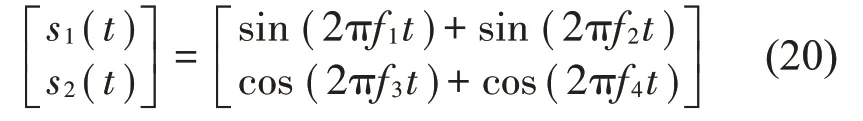


3 实验研究



4 结语
